不锈钢管局部承压性能试验研究

陈希湘，王鑫涛，袁 员，陈 誉

(1.长江大学工程技术学院，湖北荆州434020; 2.长江大学城市建设学院， 湖北荆州434023)



不锈钢管局部承压性能试验研究

陈希湘1，王鑫涛2，袁 员2，陈 誉2

(1.长江大学工程技术学院，湖北荆州434020; 2.长江大学城市建设学院， 湖北荆州434023)

为研究不锈钢管和不锈钢管混凝土构件的局部承压性能，采用静力性能试验方法，对26个不同边界条件、加载条件和方式、支承板宽度和高厚比的中空不锈钢管试件及8个内灌混凝土的不锈钢管试件的腹板屈曲性能进行试验，考察了不锈钢管在端部和内部集中荷载作用下的破坏模式，给出了荷载—位移曲线以及局部承压区域应变强度分布曲线，分析了边界条件、加载条件、支承板宽度、高厚比和内灌混凝土对不锈钢管局部承压极限承载力和延性的影响。试验结果表明：支承板宽度的增大能显著提高中空不锈钢管局部受压极限承载力；其他条件相同时，腹板名义高厚比为50的中空不锈钢管试件局部受压极限承载力均明显高于腹板名义高厚比为75的试件；腹板名义高厚比为50的中空不锈钢管试件的延性均明显低于腹板名义高厚比为75的试件；其他条件相同时，中空不锈钢管内部一侧翼缘加载(IG)的局部受压极限承载力最高，内部两侧翼缘加载(ITF)的局部受压极限承载力次之，端部一侧翼缘加载(EG)和端部两侧翼缘加载(ETF)的局部受压极限承载力最低；内灌混凝土对不锈钢管局部受压极限承载力提高非常显著。

局部承压；力学性能；中空不锈钢管；内灌混凝土不锈钢管；极限承载力

0 引 言

不锈钢材料因具有优良的耐久性、低维护费用、高耐火性及美观的优点，在大跨屋盖结构、桥梁和沿海防护结构中的应用范围越来越广泛。内灌混凝土在提高不锈钢管承载力的同时避免了不锈钢管过早的发生局部屈曲。总的来说，不锈钢管混凝土综合了不锈钢与核心混凝土各自的优点，在保证不锈钢管材料性能充分发挥的同时也改善其核心混凝土的强度、塑性和韧性。

文献[1-2]对不锈钢管混凝土的发展以及不锈钢管与混凝土的粘结性能和力学性能开展了研究。文献[3-4]对我国首部《不锈钢钢结构技术规程》进行了综述，并开展了不锈钢材的基本力学性能研究。国外也对不锈钢管的力学性能开展了一些研究工作[5-7]。目前，我国研究人员主要研究不锈钢构件轴心受压[8-9]、受弯[10]、压弯[11]情况下的力学性能及其相关的稳定承载力和计算方法，而忽视了不锈钢管局部承压性能的研究。本研究以中空不锈钢管及内灌混凝土不锈钢管为研究对象，主要研究边界条件、加载方式、支承板宽度、腹板高厚比和内灌混凝土对不锈钢管局部承压性能的影响，旨在探索不锈钢管局部承压性能。

1 试验方案

1.1 试件设计

本研究共设计了34个不锈钢管试件，其中，中空不锈钢管试件26个，内灌混凝土不锈钢管试件8个。变化的参数包括不锈钢管局部承压试验的边界条件、加载方式、支承板宽度、腹板高厚比，以此全面考察不锈钢管局部承压性能。

本研究设计的2种不锈钢管截面(H×B)分别为100 mm×100 mm和75 mm×45 mm，不锈钢管翼缘厚度(tf)与腹板厚度(tw)相同，不锈钢管截面腹板高厚比(λ)分别为50和75，不锈钢管试件材料均为无缝SUS302不锈钢钢材，加载时不锈钢管截面摆放位置如图1所示。

(a) 方形截面 (b) 矩形截面

图1 不锈钢管截面摆放位置示意图

Fig.1 Definition of symbols of stainless steel tube

本研究共设计了4种边界条件和加载方式，分别为端部一侧翼缘加载(EG)、端部两侧翼缘加载(ETF)、内部一侧翼缘加载(IG)和内部两侧翼缘加载(ITF)，如图2所示。试件编号以及对应的参数与极限承载力见表1。试件编号以相应的参数来命名，由5部分组成，各部分用“-”隔开。第一部分大写英文字母SHSSS和RHSSS分别表示方形不锈钢管(Square Hollow Section Stainless Steel Tube)和矩形不锈钢管(Rectangle Hollow Section Stainless Steel Tube)；第二部分由截面高度(H)×截面宽度(B)组成；第三部分表示不同的边界条件和加载方式的英文简写(EG、ETF、IG和ITF)；第四部分英文字母“H”、“C”分别表示无内灌混凝土中空(Hollow)和有内灌混凝土(Concrete)；第五部分由支承板宽度(Bearing Length)英文首字母和数字表示。比如，SHSSS-100×100-ITF-H-BL50则为截面(H×B)为100×100的无内灌混凝土中空方形不锈钢管在内部两侧翼缘加载且支承板宽度为50 mm。为检验试验结果的可靠度，特意安排了两组重复的试验，试件编号为SHSSS-100×100-ITF-H-BL50和RHSSS-75×45-ITF-H-BL50。试件编号后加①表示第一次试验，试件编号后加②表示第二次试验。

图2 四种边界和加载条件下试验照片

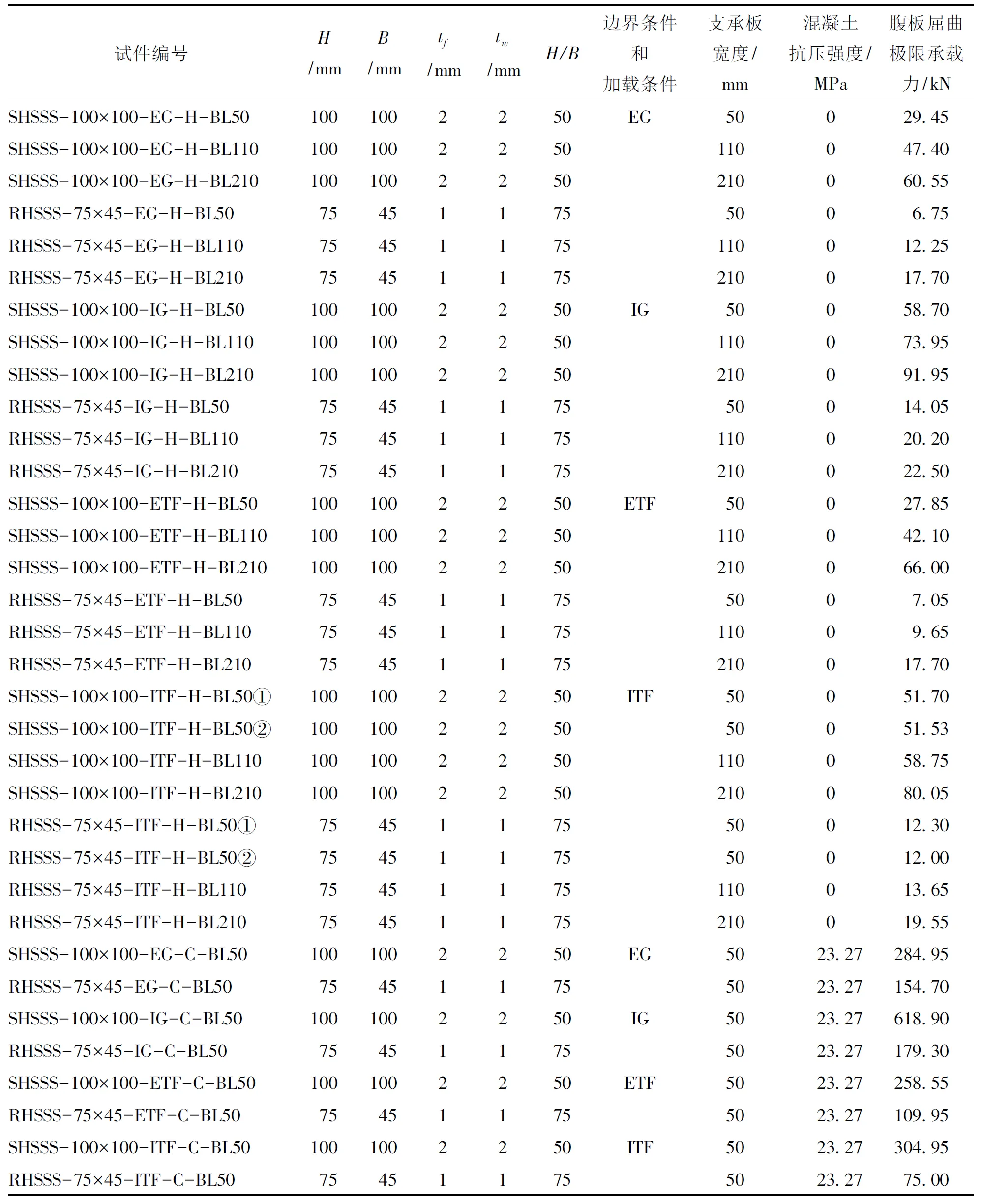
试件编号H/mmB/mmtf/mmtw/mmH/B边界条件和加载条件支承板宽度/mm混凝土抗压强度/MPa腹板屈曲极限承载力/kNSHSSS-100×100-EG-H-BL501001002250EG50029.45SHSSS-100×100-EG-H-BL1101001002250110047.40SHSSS-100×100-EG-H-BL2101001002250210060.55RHSSS-75×45-EG-H-BL50754511755006.75RHSSS-75×45-EG-H-BL11075451175110012.25RHSSS-75×45-EG-H-BL21075451175210017.70SHSSS-100×100-IG-H-BL501001002250IG50058.70SHSSS-100×100-IG-H-BL1101001002250110073.95SHSSS-100×100-IG-H-BL2101001002250210091.95RHSSS-75×45-IG-H-BL507545117550014.05RHSSS-75×45-IG-H-BL11075451175110020.20RHSSS-75×45-IG-H-BL21075451175210022.50SHSSS-100×100-ETF-H-BL501001002250ETF50027.85SHSSS-100×100-ETF-H-BL1101001002250110042.10SHSSS-100×100-ETF-H-BL2101001002250210066.00RHSSS-75×45-ETF-H-BL50754511755007.05RHSSS-75×45-ETF-H-BL1107545117511009.65RHSSS-75×45-ETF-H-BL21075451175210017.70SHSSS-100×100-ITF-H-BL50①1001002250ITF50051.70SHSSS-100×100-ITF-H-BL50②100100225050051.53SHSSS-100×100-ITF-H-BL1101001002250110058.75SHSSS-100×100-ITF-H-BL2101001002250210080.05RHSSS-75×45-ITF-H-BL50①7545117550012.30RHSSS-75×45-ITF-H-BL50②7545117550012.00RHSSS-75×45-ITF-H-BL11075451175110013.65RHSSS-75×45-ITF-H-BL21075451175210019.55SHSSS-100×100-EG-C-BL501001002250EG5023.27284.95RHSSS-75×45-EG-C-BL50754511755023.27154.70SHSSS-100×100-IG-C-BL501001002250IG5023.27618.90RHSSS-75×45-IG-C-BL50754511755023.27179.30SHSSS-100×100-ETF-C-BL501001002250ETF5023.27258.55RHSSS-75×45-ETF-C-BL50754511755023.27109.95SHSSS-100×100-ITF-C-BL501001002250ITF5023.27304.95RHSSS-75×45-ITF-C-BL50754511755023.2775.00

1.2 材料性能

不锈钢管材料性能试验结果见表2。本试验所用混凝土实测抗压强度由3个150 mm×150 mm×150 mm的混凝土立方体试块的抗压强度计算所得。3个混凝土立方体试块在浇灌混凝土不锈钢管试件期间同时制作并同条件养护。混凝土立方体试块抗压强度试验结果见表3。

试件一与试件三的抗压强度的差异值超过中间值(23.27 MPa)的15%，故把最大值(27.41 MPa)与最小值(21.65 MPa)一并舍除，取中间值(23.27 MPa)作为该组试件的抗压强度标准值，即该试验内灌混凝土抗压强度实测值。

表2 不锈钢管材性试验结果

表3 混凝土立方体试块抗压强度试验结果

1.3 加载和测试方案设计

本试验为单调分级静力加载，采用DH3816采集应变数据，通过Max Test软件观察并记录位移。同时，在支承板中线对应的不锈钢管局部承压的腹板上均匀布置了3个直角应变花，分别位于距上下翼缘的外表面5 mm的腹板上部、中部和下部，编号从上至下依次为T1、T2、T3。每个直角应变花由3个BX120-3CA电阻应变计从纵向、横向、45度倾斜方向组成，布置如图3。

2 试验结果与分析

2.1 破坏模式

为校核试验结果的可靠度，安排两组重复试验，试件为SHSSS-100×100-ITF-H-BL50和RHSSS-75×45-ITF-H-BL50，重复试验结果接近第一次试验，误差分别为0.7%和2.5%，均在允许误差范围内。无内灌混凝土中空不锈钢管试件的破坏模式为破坏区域内腹板平面外屈曲，向外鼓出，腹板出现塑性铰区域；端部一侧翼缘加载(EG)与端部两侧翼缘加载(ETF)时的翼缘破坏模式基本上为上下翼缘截面呈抛物线状向内凹陷；内部一侧翼缘加载(IG)时为加载面破坏区域上翼缘呈抛物线状向内凹陷；内部两侧翼缘加载(ITF)时的翼缘破坏模式为上、下翼缘呈抛物线状向内凹陷；端部一侧翼缘加载(EG)时，支承板宽度为210 mm时，上翼缘整体平面下陷。试件因腹板鼓出和翼缘凹陷变形过大，加载后期直角刚域变成钝角塑性区域，母材在内倒角部位会首先出现裂缝，并向外延伸直至开裂，最终延纵向开裂，破坏模式如图4所示。

(a) EG (b) IG

(c) ETF (d) ITF

图4 中空管破坏模式

Fig.4 Failure modes of hollow tube

内灌混凝土不锈钢管试件的破坏模式为破坏区域内加载端翼缘整体平面下陷、无呈抛物线状凹陷现象；破坏区域内混凝土均被压溃，端部加载情况下的试件内灌混凝土为典型的“环箍”效应破坏模式；试件未加载端可明显观察到其内灌混凝土被挤出；端部一侧翼缘加载(EG)与端部两侧翼缘加载(ETF)时，腹板平面外屈曲，向外鼓出，腹板中部出现塑性铰区域，破坏区域边缘腹板呈直线状凸出；内部一侧翼缘加载(IG)时，破坏区域内加载侧附近腹板上部变为呈折线状向外凸出。内部两侧翼缘加载(ITF)时，破坏区域内两侧加载侧腹板上部变为呈折线状向外凸出，如图5所示。

(a) EG (b) IG

(c) ETF (d) ITF

图5 内灌混凝土管破坏模式

Fig.5 Failure modes of concrete filled tube

2.2 支承板宽度对局部承压极限承载力的影响

不同支承板宽度下的无内灌混凝土中空不锈钢管局部承压极限承载力分析结果见表3。在试件的尺寸范围内，支承板宽度的增大能显著提高无内灌混凝土中空不锈钢管局部承压极限承载力，两者基本上呈线性关系，且与加载条件和边界条件有关。支承板宽度的增大对内部加载条件下无内灌混凝土中空不锈钢管局部承压极限承载力的提高幅度分别为34%[IG，Pcr(BL=110)/Pcr(BL=50)]、59%[IG，Pcr(BL=210)/Pcr(BL=50)]、13%[ITF，Pcr(BL=110)/Pcr(BL=50)]和57%[ITF，Pcr(BL=210)/Pcr(BL=50)],明显低于端部加载条件下的提高幅度，其值分别为71%[EG，Pcr(BL=110)/Pcr(BL=50)]、134%[EG，Pcr(BL=210)/Pcr(BL=50)]、44%[ETF，Pcr(BL=110)/Pcr(BL=50)]和144%[ETF，Pcr(BL=210)/Pcr(BL=50)]。这表明端部加载条件下增大支承板宽度对提高无内灌混凝土中空不锈钢管局部承压极限承载力比内部加载条件下更明显。支承板宽度从50 mm增加为110 mm时，在端部一侧翼缘加载(EG)条件下无内灌混凝土中空不锈钢管局部承压极限承载力提高幅度最大为71%，在内部两侧翼缘加载(ITF)条件下最低为13%；支承板宽度从50 mm增加为210 mm时，在内部翼缘加载(IG和ITF)条件下提高幅度近似，为58%左右；在端部两侧翼缘加载(ETF)条件下提高幅度最大为144%，在内部两侧翼缘加载(ITF)条件下提高幅度最低为57%。

表3 不同支承板宽度下的无内灌混凝土中空不锈钢管局部承压极限承载力分析结果

2.3 腹板高厚比对局部承压极限承载力的影响

在支承板宽度为50 mm、110 mm和210 mm时，在试验所覆盖的高厚比范围内，局部承压极限承载力极大值点均出现在名义腹板高厚比为50的点位上，局部承压极限承载力随高厚比的增加而降低。

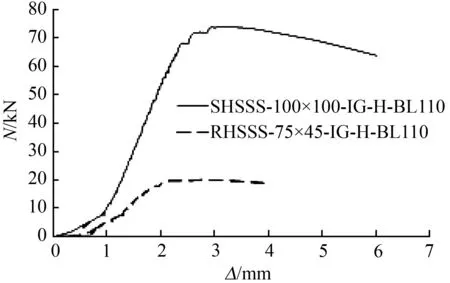
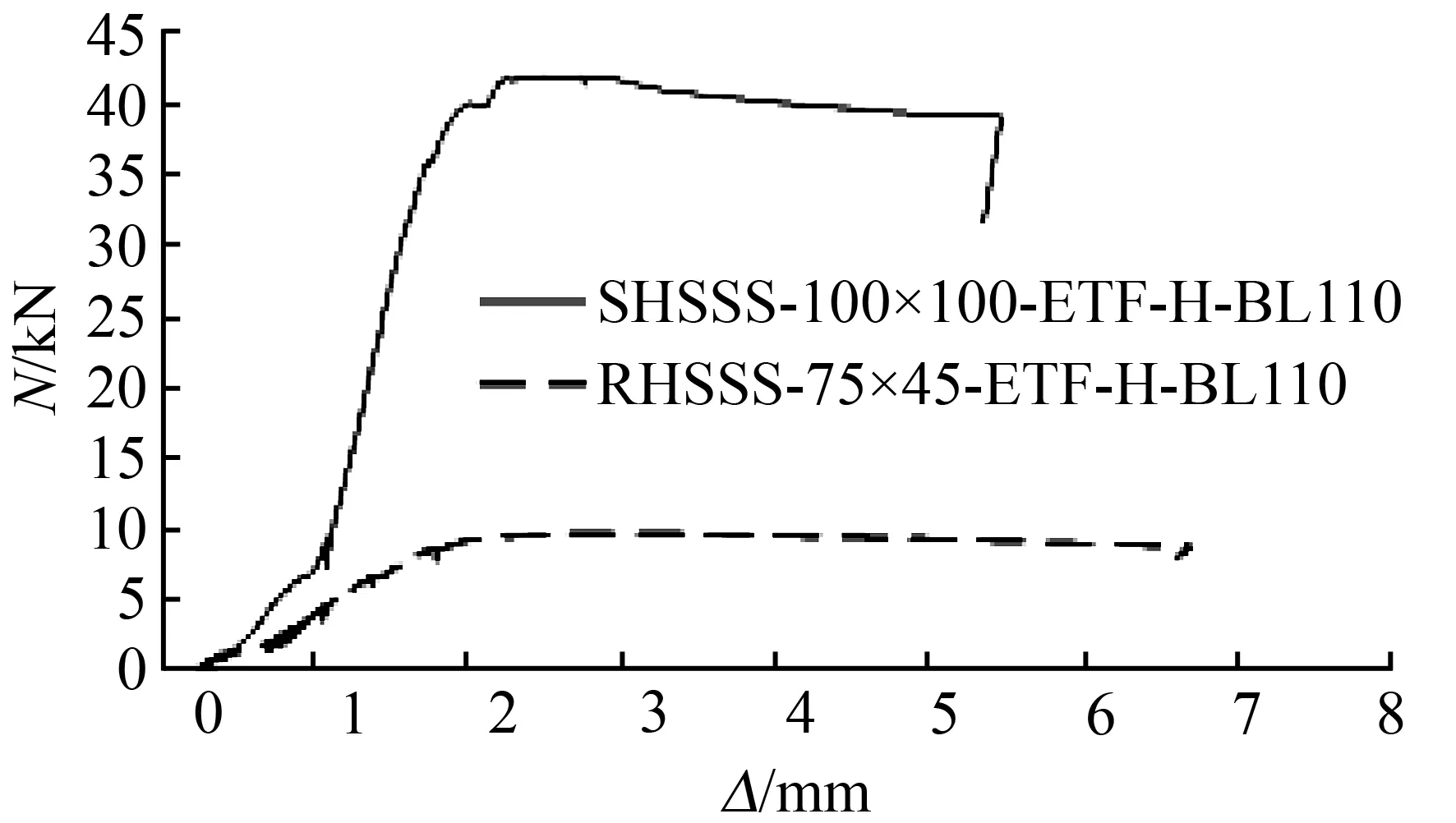
不同腹板高厚比下的无内灌混凝土中空不锈钢管局部承压荷载—位移曲线见图6。无内灌混凝土中空不锈钢管试件屈服时竖向位移ΔA和对应于极限承载力的竖向位移ΔB的对比如表4。支承板宽度为110 mm时，在试验所覆盖的高厚比范围内，名义高厚比为50时局部承压极限承载力较高，但达到局部承压极限承载力后荷载下降较名义高厚比为75时的快；延性不如名义高厚比为75时的试件,即腹板高厚比越大，初始刚度越小但延性较好。

(a) EG

(b) IOF

(c) ETF

(d) ITF

图6 不同腹板高厚比下无内灌混凝土中空不锈钢管局部承压荷载—位移曲线

Fig.6 Load-displacement of stainless steel hollow seetion tubes under local load with different web slenderness

表4 无内灌混凝土中空不锈钢管延性对比

2.4 边界和加载条件对局部承压极限承载力的影响

不同边界条件和加载方式对无内灌混凝土中空不锈钢管局部承压极限承载力分析结果见图7。其他条件相同时，内部一侧翼缘加载(IG)的局部承压极限承载力最高，内部两侧翼缘加载(ITF)的局部承压极限承载力次之，端部一侧翼缘加载(EG)和端部两侧翼缘加载(ETF)的局部承压极限承载力最低。支承板宽度为50 mm和110 mm时，内部加载条件下的局部承压极限承载力均高于端部加载条件下的局部承压极限承载力，端部一侧翼缘加载(EG)较端部两侧翼缘加载(ETF)的局部承压极限承载力高；但支撑板宽度为210 mm时，随腹板高厚比的增大，该顺序个别被打乱。

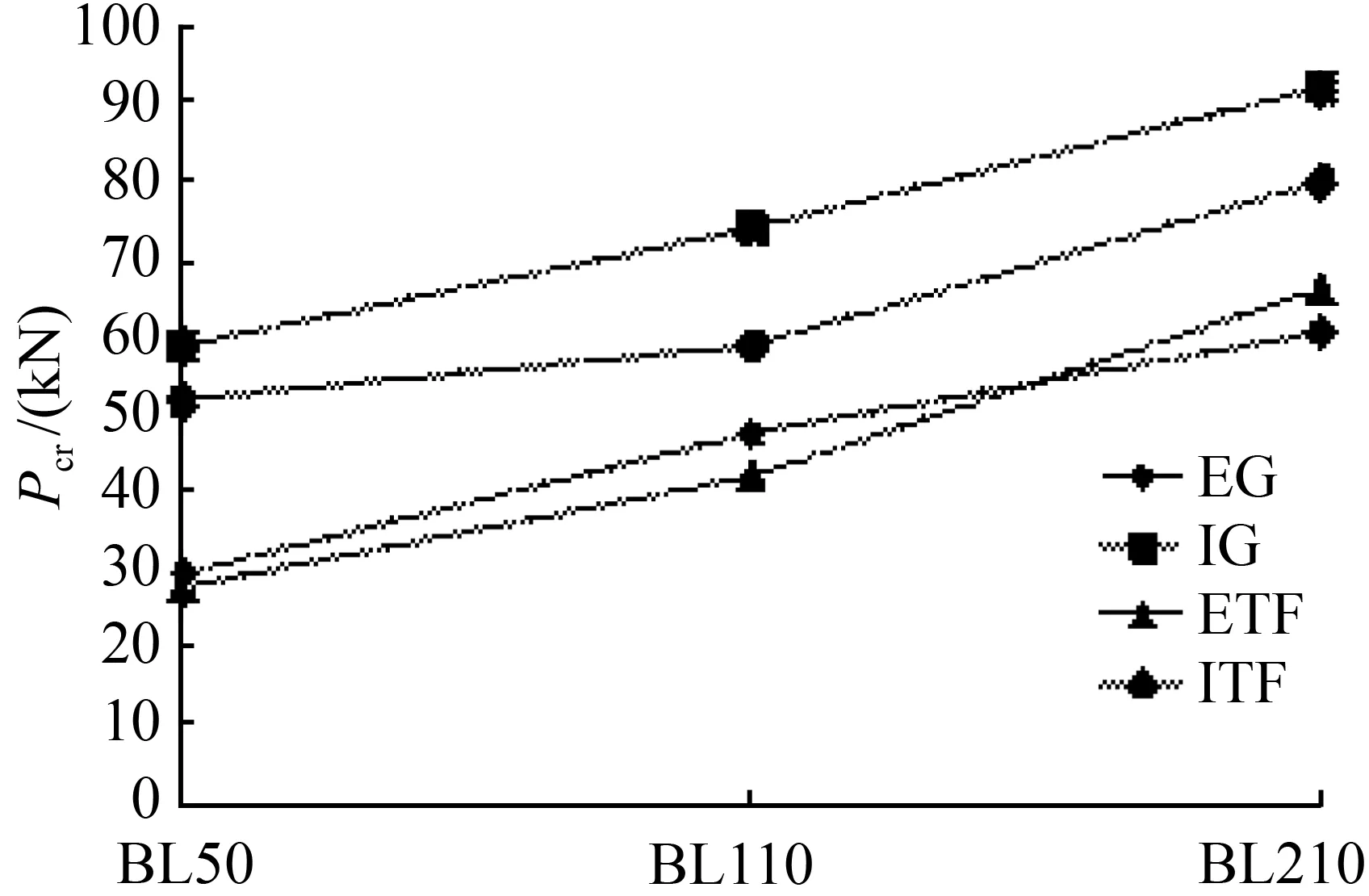
图7 不同边界和加载条件下无内灌混凝土中空不锈钢管局部承压极限承载力分析

不同边界条件和加载方式对无内灌混凝土中空不锈钢管局部承压荷载—位移曲线见图8。无内灌混凝土中空不锈钢管试件屈服时竖向位移ΔA和对应于极限承载力的竖向位移ΔB的对比如表5。4种边界条件和加载方式下试件的初始刚度较为接近，内部加载条件下试件具有较高的局部承压极限承载力和较好的延性。

(a) 方形

(b) 矩形

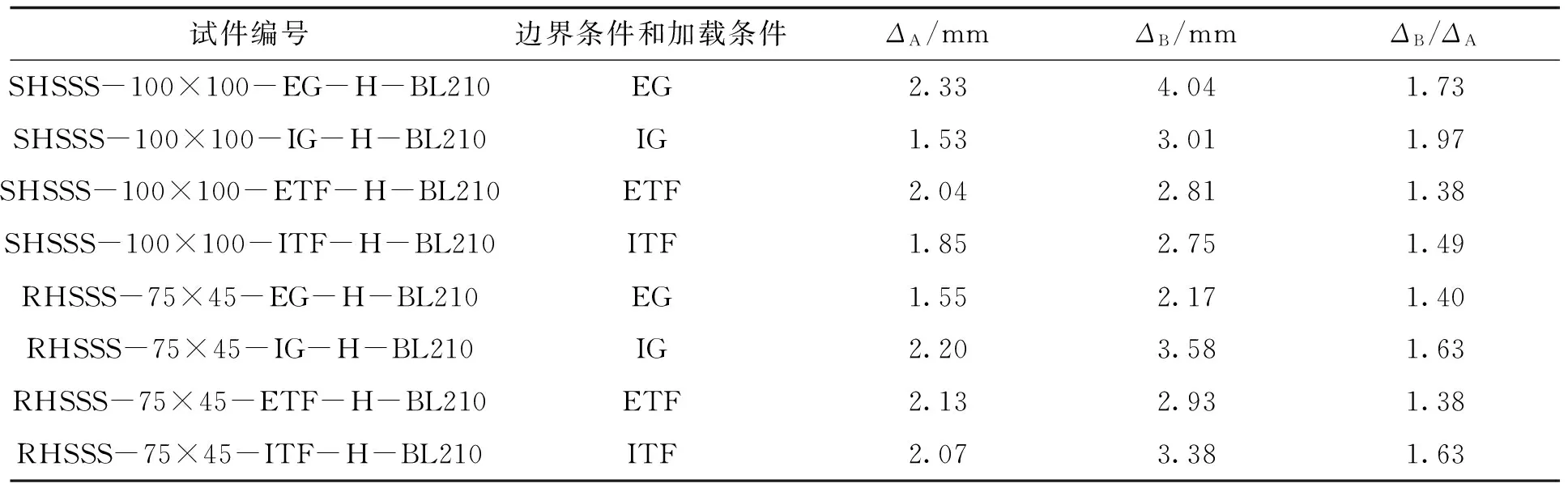
图8 不同边界和加载条件下中空不锈钢管局部承压荷载—位移曲线

支承板宽度为50 mm时，不同边界条件和加载方式对内灌混凝土不锈钢管局部承压极限承载力分析结果见图9。其他条件相同时，名义高厚比为50时的试件内部一侧翼缘加载(IG)的极限承载力最高，内部两侧翼缘加载(ITF)次之，端部一侧翼缘加载(EG)和端部两侧翼缘加载(ETF)最低；但名义高厚比为75时，随腹板高厚比的增大，该顺序个别被打乱。

不同边界条件和加载方式对内灌混凝土不锈钢管局部承压荷载—位移曲线见图10。在不锈钢管内部混凝土与不锈钢管腹板脱离前后，4种边界条件和加载方式下试件的初始刚度均较为接近，而且4种边界条件和加载方式下试件到达局部承压极限承载力之后，荷载下降速度均较快，延性较差。

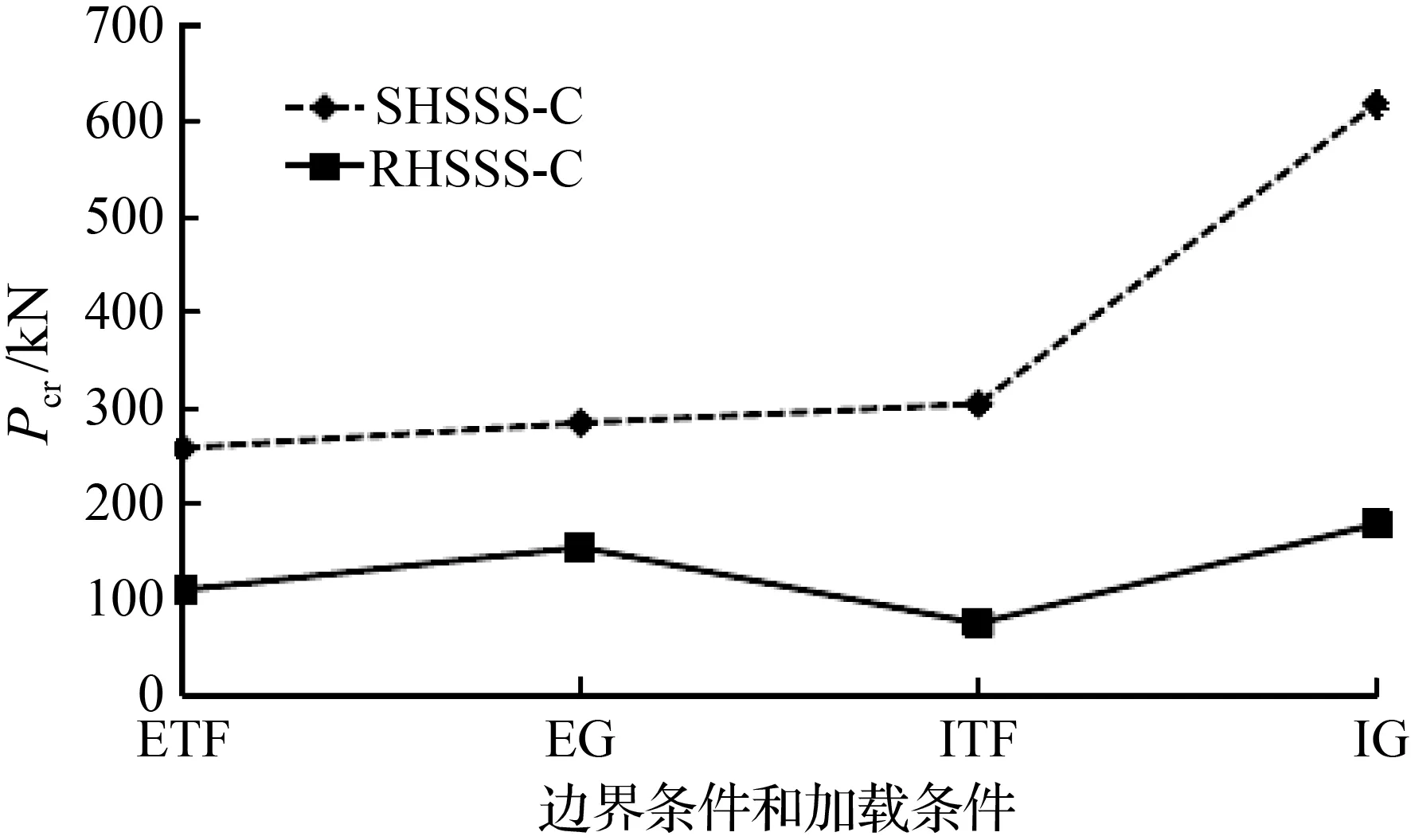
图9 不同边界和加载条件下内灌混凝土不锈钢管局部承压极限承载力分析

(a)方形

(b) 矩形

图10 不同边界和加载条件下内灌混凝土不锈钢管局部承压荷载—位移曲线

Fig.10 Load-displacement of stainless steel composite section tubes local load with different boundary and loading conditions

2.5 内灌混凝土对局部承压极限承载力的影响

支承板宽度为50 mm时，有无内灌混凝土不锈钢管局部承压极限承载力的分析结果见表6。其余条件相同的情况下，内部两侧翼缘加载(ITF)时局部承压极限承载力提高的幅度最低，端部一侧翼缘加载(EG)的条件下高厚比为75时提高的幅度最高，但由于高厚比为50的试件截面面积较大，其局部承压极限承载力增值反而较大。SHSSS-100×100-IG-C-BL50试件的局部承压极限承载力增值量最大，为560.2 kN，RHSSS-75×45-ITF-H-BL50试件的局部承压极限承载力增值最小，为62.7 kN。支承板宽度为50 mm时，4种边界条件和加载方式下的试件中SHSSS-100×100试件的局部承压极限承载力增值均比对相应的RHSSS-75×45试件高。其他条件相同时，内部一侧翼缘加载(IG)条件下试件局部承压极限承载力增值均比其他3种条件的大。随着试件截面面积的增大，端部一侧翼缘加载情况下局部承压极限承载力提高的幅度相对于其他3种加载情况下的明显。

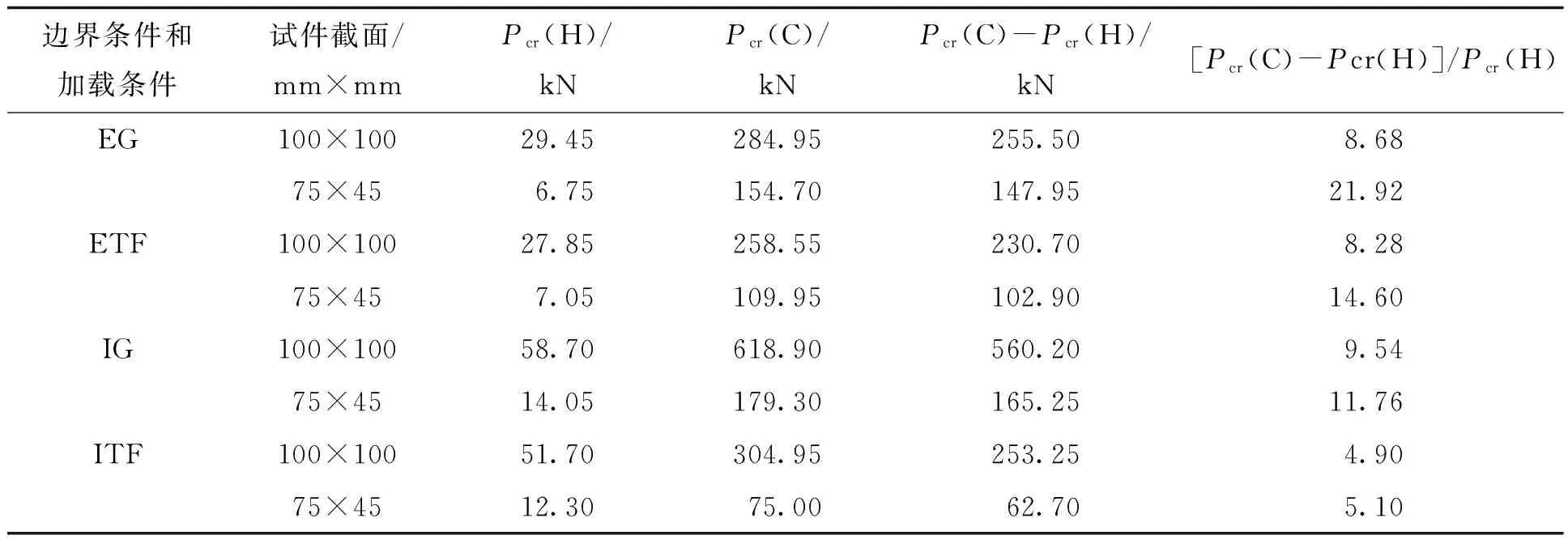
表6 有无内灌混凝土不锈钢管局部承压极限承载力

注：Pcr(H)和Pcr(C)分别为空管和灌混凝土不锈钢管局部承压承载力。

2.6 局部承压腹板应变分析

不锈钢管局部承压腹板上T1、T2、T3测点应变强度[12]分布见表7。应变测点分布见图3。由表7可见，内灌混凝土造成不锈钢管局部承压腹板应变最大位置发生变化，同时造成腹板进入屈服阶段后其塑性铰区域的面积扩大。

表7 T1、T2、T3测点应变强度分布对比

注：T1为腹板上部测点;T2为腹板中部测点;T3为腹板下部测点。

3 结 论

通过不同边界条件、加载条件、支承板宽度和高厚比的26个中空不锈钢管试件及8个内灌混凝土的不锈钢管试件的腹板屈曲性能试验，得到以下结论：

①支承板宽度的增大能显著提高中空不锈钢管局部承压极限承载力。

②其他条件相同时，腹板名义高厚比为50的无内灌混凝土中空不锈钢管局部承压极限承载力均明显高于腹板名义高厚比为75的无内灌混凝土中空不锈钢管局部承压极限承载力。

③其他情况条件时，无内灌混凝土中空不锈钢管内部一侧翼缘加载(IG)的局部承压极限承载力最高，内部两侧翼缘加载(ITF)的局部承压极限承载力次之，端部一侧翼缘加载(EG)和端部两侧翼缘加载(ETF)的局部承压极限承载力最低。

④内灌混凝土对不锈钢管局部承压极限承载力提高最为显著；不锈钢管局部承压极限承载力增加量与不锈钢管截面面积、边界条件和加载方式有关；其他条件相同时，内部一侧翼缘加载(IG)情况下不锈钢管局部承压极限承载力增加量最大；截面为75×45的情况下，其他条件相同时，内部一侧翼缘加载(IG)情况下不锈钢管局部承压极限承载力增加量最大，而端部一侧翼缘加载(EG)情况下不锈钢管局部承压极限承载力提高的幅度最大。

[1] 廖飞宇，陶忠.不锈钢管混凝土的发展综述[J]. 工业建筑,2009,39(4)：114-118.

[2] 刘保材.不锈钢管混凝土粘结性能及在长期荷载作用下力学性能研究[D]. 福州：福州大学,2011.

[3] 舒赣平，王元清，袁焕鑫,等.《不锈钢结构技术规程》的编制及内容简介[J]. 工业建筑，2015,45(12)：1-12.

[4] 郑宝峰，舒赣平，沈晓明.不锈钢材料常温力学性能试验研究[J]. 钢结构，2011,26(5)：1-55.

[5] ELLOBODY E, YOUNG B.Experimental investigation of concrete-filled cold-formed high strength stainless steel tube columns[J]. Journal of Constructional Steel Research, 2006,62(5):484-492.

[6] ELLOBODY E, YOUNG B.Design and behaviour of concrete-filled cold-formed stainless steel tube columns[J]. Engineering Structures,2006,28(4):716-728.

[7] ELLOBODY E.Nonlinear behavior of concrete-filled stainless steel stiffened slender tube Columns[J]. Thin-Walled Structures,2007,45(3):259-273.

[8] 杨璐，尚帆，赵梦晗，等.不锈钢工字形截面构件轴心受压整体稳定计算方法[J]. 湖南大学学报(自然科学报)，2016,43(3)：55-65.

[9] 郑宝峰，舒赣平，沈晓明.不锈钢冷成型管截面轴心受压构件的有限元分析[J]. 工业建筑，2012,42(5)：12-20.

[10]王元清，高博，戴国欣，等.不锈钢受弯构件承载性能的研究进展[J]. 建筑结构学报，2010,33(1)：189-194.

[11]舒赣平，郑宝峰，沈晓明.不锈钢压弯构件平面内稳定承载力计算方法研究[J]. 工业建筑，2012,42(5)：41-44.

[12]陈希湘，冯然，陈誉，等.天然气管道悬索跨越结构风致响应研究[J]. 广西大学学报(自然科学版)， 2015，40(2)：317-324.

(责任编辑 唐汉民 裴润梅)

Experimental investigation on mechanical behavior of stainless steel tube under local axial compression

CHEN Xi-xiang1, WANG Xing-tao2, YUAN Yuan2, CHEN Yu2

(1.College of Technology & Engineering, Yangtze University, Jingzhou 434020, China; 2.School of Urban Construction, Yangtze University, Jingzhou 434023, China)

To research the mechanical behavior of stainless steel tubes under local axial compression, twenty-six stainless steel tubes with different loadings, bearing length, height-to-thickness ratios were tested. Eight stainless steel tubes that were filled with concrete to enhance the local load bearing strength were tested. Failure modes, load-end vertical displacement and strain intensity distribution curves were presented. The effects of boundary conditions, loading conditions, bearing length, height-to-thickness ratio and filling concrete on the ultimate local load carrying capacity and the ductility of stainless steel tubes were also studied. It was found that, as the bearing length increases, the effect of bearing length on the ultimate local load carrying capacity of the tubes is more obvious. Under the same condition, the ultimate local load carrying capacity of the tube with the height-to-thickness ratio of 50 is all larger than that of the tube with the height-to-thickness ratio of 75,but the ductility of the tubes is just the opposite. The ultimate local load carrying capacity of the tubes under Interior-Ground(IG) loading, Interior-Two-Flange(ITF) loading, End-Ground(EG) loading and End-Two-Flange loading decreases successively. The effect of filling concrete on the ultimate local load carrying capacity of stainless steel tubes is obvious.

local bearing; mechanical behavior; stainless steel hollow sections tubes; stainless steel composite sections tubes; ultimate carrying capacity

2016-06-28；

2016-07-26

国家自然科学基金资助项目(51278209, 51478047);长江大学工程技术学院科学发展基金资助项目(15j0402)

陈 誉(1978.4—)，男，湖北公安人，长江大学教授，博士;E-mail: kinkingingin@163.com。

陈希湘，王鑫涛，袁员,等.不锈钢管局部承压性能试验研究[J].广西大学学报(自然科学版)，2016，41(5)：1330-1341.

10.13624/j.cnki.issn.1001-7445.2016.1330

TU392.3

A

1001-7445(2016)05-1330-12