生命探测履带车过沟性能的仿真分析

陈亚,尤伟,章易程,刘晓静,陈佳萍,谭斌

(中南大学 交通运输工程学院,湖南 长沙 410075)



生命探测履带车过沟性能的仿真分析

陈亚,尤伟,章易程,刘晓静,陈佳萍,谭斌

(中南大学 交通运输工程学院,湖南 长沙 410075)

通过运用多体动力学分析软件 RecurDyn对履带车的过沟工况进行动力学仿真，分析履带车过沟不同阶段的运动状态，提出速率比来衡量履带车的过沟性能，并以此研究履带车的重心位置等因素对其过沟性能的影响，为过沟性能高的履带车设计提供理论依据。研究结果表明：采用速率比能较好地衡量履带车结构对过沟性能的影响；重心位置相对于几何中心靠前、靠下均有利于过沟性能的提升。

履带车；过沟；性能；仿真

当铁路灾难事故发生后，由于线路中断无法快速调配救援物资，故搜救生命并尽快恢复通车的要求使得时间成为救援工作的关键要素[1]。如果能研发一种能装载生命探测仪的小车进行生命探测，就可以提高搜救效率，减少救援时间。由于履带车具有良好的地面适应能力与机动性能，往往成为复杂灾难现场搜救的机器人。近年来,国内外学者开展了有关履带车的研究分析。Huh等[2]通过设计控制试验系统，模拟了履带张紧力的研究模型，分析了不同工况下履带张紧力状态。A1-Milli 等[3]分析了履带车整体重力及横向阻力对转向特性的影响规律，并得到了转向阻力矩计算模型。王国强等[4]通过总结不同特性、不同速度运行的履带车模型，建立了RTVPM高速履带车模型和NTVPM低速履带车模型。宋晗等[5]运用多刚体虚拟样机模型进行计算机模拟仿真试验，研究分析了不同地面特性下的履带张紧力。张季琴等[6]通过正交试验设计方法研究了履带拖拉机的牵引附着性能。装载生命探测仪的履带车与工程或军事上的履带车相比，往往需要具有小巧、低速以及灵活越障性能等要求，以确保全面、仔细而准确地进行生命探测。国内外的现有研究大多基于工程履带车或军事履带车的动力学研究等，虽然对履带车的动力学设计有普遍的指导作用，但迄今为止并没有关于履带车灵活越障性能的研究报道。

为了确保履带车翻转后能继续运动的需要，本文采用一种上下、左右、前后均对称的履带车结构，生命探测仪则安装在车体中央部位。过沟是履带车最常见的越障形式。本文以此结构进行履带车过沟性能的分析，提出过沟性能指标，并讨论初始速度及履带车重心等因素对其影响规律。

1　履带车行驶的数学模型

1.1直线行驶运动分析

当履带车作直线行驶时，车体作直线平移运动，而履带环作卷绕运动。履带车各点的速度如图1所示，设车体与履带环装置共同的前进速度为vq，履带环在环绕着车身作往复的卷绕运动，其卷绕速度为vx，取履带上任一点的瞬时绝对速度为vj，设前进速度vq与绝对速度之间vj的夹角为θ，则有：

(1)

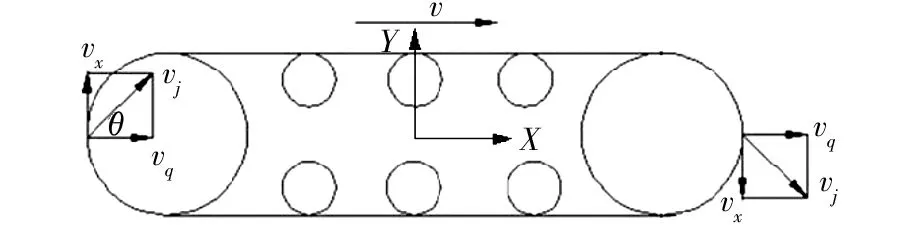
图1　履带的速度分析Fig.1 Analysis of track speed

如图1所示，履带环的卷绕运动方向为顺时针。若为水平地面，对于接地履带区间，有θ=π，则其中的点的绝对速度为

vj=vq-vx

(2)

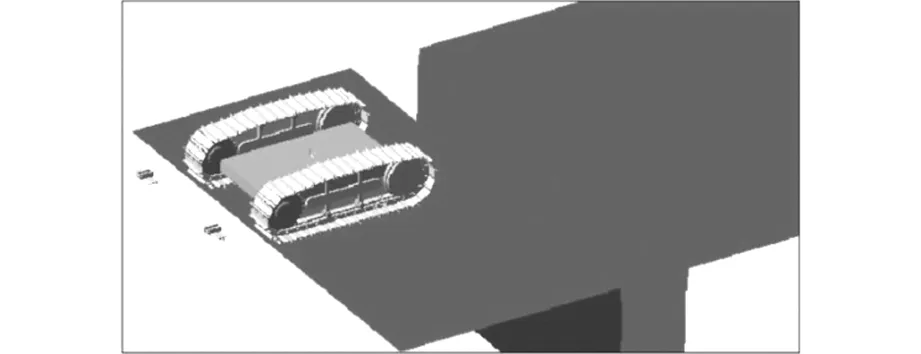
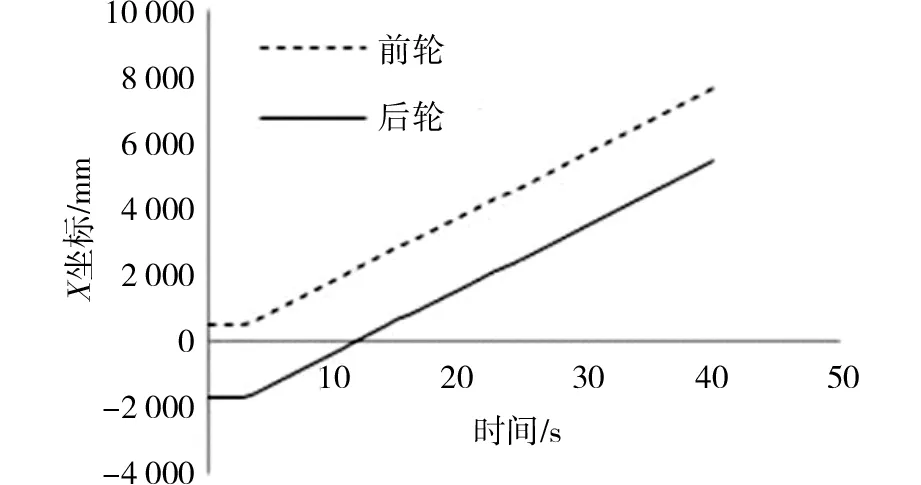
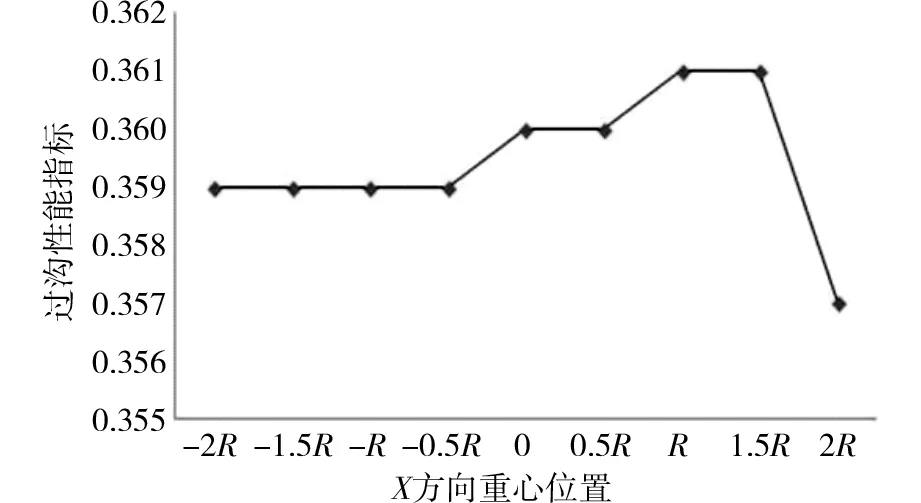
若vq

若vq>vx，vj>0，此时接地履带区间滑动的方向与履带车运动的方向相同，这时产生滑移。

接地履带区间上某点的滑转速度与履带环的卷绕速度的比值称为滑转系数，接地履带区间的滑转程度可以用滑转系数σ来表示[7]

(3)

令履带车的行驶速度v=vq，则有：

v=(1-σ)vx

(4)

由式(4)可知几种行驶情况如下：

1)当σ=0时，即v=vx，为履带车的理论行驶速度；

2)当0<σ<1时，即v

3)当σ=1时，即v=0，履带原地空转，履带车行驶速度完全损失，称为完全滑转；

4)当σ<0时，即v>vx，履带车行驶速度大于履带的卷绕速度，履带相对于地面产生滑移；

5)当履带被制死时，即vx=0，履带车依赖本身的动能向前滑移，表现为完全滑移。

1.2履带车辆的驱动力

履带车行驶过程中，土壤给履带的驱动力与土壤相关特性参数密切相关。在利用多体动力学仿真软件 RecurDyn进行分析之前也需要确定履带车的行驶阻力。

应用压力-沉陷关系式，履带式车辆的沉陷量z0为[8]

(5)

式中：W为整车质量；ks为内聚的土壤变形模量；kc为内摩擦的土壤变形模量；b为履带板的宽度；n为土壤的变形指数。

履带车压过土壤后，将形成了长为L，宽b和深z0的车辙，其行驶驱动力FRC为[7]

(6)

式中:kφ为摩擦变形模量，由土壤刚性成分所决定。

2　过沟过程分析

采用多体动力学仿真软件 RecurDyn[9-10]，建立如图2所示的低速履带车简化模型Track(LM)。车轮半径R=365 mm，两轮轴线的初始距离为轮半径的6倍，即6R。采用深沟地面Ground模型。沟坑的初始宽度为w=3R。履带车以后轮为驱动轮、前轮为从动轮沿着X正方向运动，重力方向为Y负方向，宽度方向为Z方向。

图2　履带车过沟模型Fig.2 Model of pit-crossing of tracked vehicle

通过仿真分析，履带车过沟可以划分为以下5个阶段，如图3所示。

(a)过沟准备阶段;(b)前轮悬空阶段;(c)两轮支撑阶段;(d)后轮悬空阶段;(e)恢复平稳行驶阶段图3　履带车过沟阶段Fig.3 Stages of pit-crossing of tracked vehicle

a)过沟准备阶段：在水平路面，履带车由静止开始加速至恒定速度，前轮到达沟坑左边缘的过程。

b)前轮悬空阶段：履带车前轮离开沟坑左边缘进入沟坑内的过程。

c)两轮支撑阶段：履带车前后两轮支撑在沟坑左右两边缘的过程。

d)后轮悬空阶段：履带车后轮脱离沟坑左边缘到达右边缘的过程。

e)恢复平稳行驶阶段：履带车脱离沟坑右边缘直至平稳前进的过程。

如图4表示履带车过沟时俯仰角的变化。在5 s以前，履带车处于过沟准备阶段，由于启动时或前轮接触沟坑左边缘时车与地面的相互作用，履带车会有微小振动，俯仰角也就有微小波动，但均接近0。在5～6.7 s之间，履带车处于前轮悬空阶段，此时履带车体重心离沟坑左边缘越远，履带车头部下倾越严重，若沟坑太宽，则履带车会坠落。6.7～8.5 s之间，履带车处于两轮支撑阶段；从前轮碰到沟坑的右边缘开始，履带车下倾角度逐渐变小；当前轮轴线位于沟坑右边缘的正上方时，履带车的俯仰角变为0。8.5～10.2 s之间，履带车处于后轮悬空阶段，随着履带车重心逐渐脱离沟坑的左边缘，履带车后仰角度逐渐变大；当10.2 s时重心正好位于沟坑右边缘的正上方，后仰角达到最大值。10.2～15 s之间为履带车处于恢复平稳行驶的阶段，由于履带车的惯性，即使在后轮脱离沟坑的右边缘后，还会以一定的后仰角度向前行驶，但因重心作用，履带车的后仰角逐渐变小，当达到15 s以后，履带车行驶稳定，至此，过沟过程完成。

图4　履带车俯仰角变化曲线Fig.4 Curves of tracked vehicle pitch angle

3　过沟性能分析

3.1过沟性能指标

(7)

(8)

式中:w为沟坑的宽度；t为过沟时间。

为了确定过沟起讫时间的方便，不妨忽略过沟后恢复平稳的时间，以前轮轴线正好在沟坑左边缘正上方的时刻为起始时刻，以后轮轴线处于沟坑右边缘正上方的时刻为过沟的结束时刻。

过沟性能指标越大，则说明在过沟的过程中，平均速度与初始速度的比值越大，也就说明了过沟性能越好，反之则过沟性能越差。当履带车不能跨过沟坑时，可以定义过沟时间t无穷大，则：rp=0 。

设履带车的重心与几何中心重合，其坐标为(0，0，0)，当驱动轮的初始速度为90°/s时，图5表示前、后轮轴线的X坐标随时间变化规律，履带车启动后的短暂时间内，其轴线的X坐标会保持不变，这是由于地面的松软性使得履带车与地面接触形成完全滑转现象。过沟的起讫时间可以根据轴线的X坐标来判定。

图5　前、后轮轴线X坐标Fig.5 X coordinate of front and rear wheel axis

3.2影响因素分析

选取初始速度与履带车体重心位置作为影响因素进行分析。

设重心坐标为(0，0，0)，后轮的半径R=365 mm，并以w=3R作为沟宽。

3.2.1初始速度

表1表明，履带车初速度越大，过沟准备时间越短，过沟开始时间越早，过沟结束时间也越早，即履带车初始速度越大，过沟时间越短，反之则越长，但过沟性能指标几乎保持不变，即通过沟坑的能力几乎不变。这说明该过沟性能指标可以较好地过滤初始速度的影响，以反映几何结构对过沟性能的影响。

表1初始速度对过沟性能指标的影响

Table 1 The impact of initial speed on pit-crossing performance

初始速度/(°/s)过沟开始时刻/s过沟结束时刻/s过沟所用时间/s过沟性能指标3010.7328.8618.130.360606.8715.959.080.359905.5711.636.060.3591204.939.434.460.3591504.558.193.640.359

3.2.2重心的X坐标

表2表明，当初始速度为30 °/s时，重心Y坐标为0时，X坐标对过沟性能指标的影响规律。其中，符号“-”代表重心向与运动方向相反的方向偏移, “+”表示重心向与运动方向相同的方向偏移。

表2　X坐标对过沟性能指标的影响Table 2 Impact of X coordinate on pit-crossing performance

表2表明：重心靠后将因为过沟准备时间增加而导致推迟过沟开始时间，这是由于重心适当前移可以使履带与地面有较好的接触而增加驱动力。若采用图6来表示过沟性能指标可以明显看到：当重心位置相对中心位置后移不利于过沟，如果重心位置相对中心位置适当前移有利于提高过沟性能，这是由于以下两因素综合作用的效果：重心后移会增加准备阶段的时间、增加恢复平稳阶段的时间，而过多前移则会因为前轮因更大重力矩而下倾更多，从而增加前轮悬空阶段的时间。

图6　过沟性能指标变化曲线Fig.6 Curves of pit-crossing performance

3.2.3重心的Y坐标

由于履带车的重心在Y方向的高度不能超过履带的上下高度界限，否则会影响履带车顺利越障，因此设置其上下浮动量为0.25R。表3表示初始速度固定为30°/s，X坐标为0时，Y坐标对过沟性能指标的影响。其中，符号“-”表示重心自中心下移；“+”表示重心自中心上移。

表3　Y坐标对过沟性能指标的影响Table 2 Impact of Y coordinate on pit-crossing performance

由表3可知，高度方向的Y坐标对过沟的开始时刻没有影响，这是因为在直线行驶过程中，履带车所受到的地面提供的驱动力并未受到影响。此外，表3还表明：重心下移则会使得过沟结束得早，这是由于重心下移有利于前轮悬空时减小倾覆力臂而减小车下倾程度，同时由于重心低而具有较快恢复平稳的缘故。所以，重心降低有利于提高过沟性能指标。

4　结论

1)采用平均速度比初始速度作为过沟性能指标，较好地反映了履带车结构对过沟性能的影响；

2)履带车重心位置相对于其几何中心稍靠前、靠下的位置有利于其完成过沟。

[1] 张彦春, 范艳萍, 杨小礼. 铁路突发事件应急物资优化调配[J]. 铁道科学与工程学报,2011，8(6):103-106.

ZHANG Yanchun, FAN Yanping, YANG Xiaoli. Optimization on railway emergency materials dispatching[J]. Journal of Railway Science and Engineering, 2011，8(6):103-106.

[2] Huh K, Chung C C, Kim I M, et al. Track tension controller design and experimental evaluation in Tracked vehicles[J]. Journal of Dynamic Systems, Measurement, and Control, 2004, 126(4): 764-771.

[3] A1-Milli S, Seneviratne L D, Kaspar A. Track-terrain modeling and traversability prediction for tracked vehicles on soft terrain[J]. Journal of Terramechanics, 2010, 47(3): 151-160.

[4] 王国强, 张进平, 马若丁. 虚拟样机技术及其在 ADAMS 上的实践[M]. 西安: 西北工业大学出版社, 2002.

WANG Guoqiang, ZHANG Jinping, MA Ruoding.Virtual prototype technology and its practice on ADAMS[M]. Xi'an: Northwestern Polytechnical University Press,2002.

[5] 宋晗, 李晓雷. 履带动态张紧力的动力学仿真[J]. 计算机仿真, 2006, 22(9): 18-21.

SONG Han, LI Xiaolei. Dynamic simulation of track tension[J]. Computer Simulation, 2006, 22(9): 18-21.

[6] 张季琴, 杨福增, 刘世. 微型履带拖拉机牵引附着性能研究——基于正交试验[J]. 农机化研究, 2013, 35(10): 190-193.

ZHANG Jiqin, YANG Fuzeng, LIU Shi. Simulation of hydraulic steering By-wire system based on fuzzy PID control[J]. Journal of Agricultural Mechanization Research, 2013, 35(10): 190-193.

[7] 汪明德,赵毓芹,祝嘉光. 坦克行驶原理[M]. 北京: 国防工业出版社, 1983.

WANG Mingde, ZHAO Yuqin, ZHU Jiaguang.Tank driving principle[M].Beijing: National Defense Industry Press,1983.

[8] Bekker M G. Off-the-road locomotion: research and development in terramechanics[M]. Ann Arbor, MI, USA: University of Michigan Press, 1960.

[9] 马金猛, 李小凡, 姚辰, 等. 地面移动机器人越障动力学建模与分析[J]. 机器人, 2008, 30(3): 273-278.

MA Jinmeng, LI Xiaofan, YAO Chen, et al. Dynamic modeling and analysis for obstacle negotiation of ground mobile robot[J]. Robot, 2008, 30(3): 273-278.

[10] 焦晓娟, 张湝渭, 彭斌彬. RecurDyn 多体系统优化仿真技术[M].北京: 清华大学出版社, 2010.

JIAO Xiaojuan, ZHANG Jiewei, PENG Binbin. RecurDyn multi-body system simulation technology optimization[M].Beijing: Tsinghua University Press,2010.

Simulation and analysis of pit-crossing performance of life detection tracked vehicle

CHEN Ya, YOU Wei, ZHANG Yicheng, LIU Xiaojing, CHEN Jiaping, TAN Bin

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

By means of multi-body dynamics analysis software RecurDyn, some simulation analyses of pit-crossing of tracked vehicle were performed. The different movement stage of pit-crossing of tracked vehicles were then analyzed .The velocity ratio was proposed to evaluate the pit-crossing performance of tracked vehicle. Also, the gravity position which affects pit-crossing performance of tracked vehicle were studied to obtain some theoretical knowledge for design of tracked vehicle. The results show that the velocity ratio has a good effect to evaluate the influence of structure of tracked vehicle on pit-crossing performance, and the gravity position of tracked vehicle should be lower and further than geometric center in order to improve pit-crossing performance.

tracked vehicle; pit-crossing; performance; simulation

2015-12-17

湖南省自然科学基金资助项目(02A0027)

章易程(1965-)，男，湖南长沙人，副教授，博士，从事车辆动力学、摩擦学、多相流体力学与CFD技术、非标机械设计等研究；E-mail:yczhang@csu.edu.cn

U216.4

A

1672-7029(2016)10-2051-05