静动载耦合作用仰拱混凝土损伤特征的试验研究

刘宁，彭立敏，施成华

(中南大学 土木工程学院， 湖南 长沙 410075)



静动载耦合作用仰拱混凝土损伤特征的试验研究

刘宁，彭立敏，施成华

(中南大学 土木工程学院， 湖南 长沙 410075)

围岩压力和列车动载共同影响隧道仰拱结构的长期服役状态，目前，对于静载与动载耦合作用下仰拱累积损伤特征及规律的相关研究明显不足且未引入设计规范。基于此，开展用于描述不同静载引起仰拱混凝土动力累积损伤特征的试验研究，得到满足仰拱结构力学环境的混凝土累积损伤模型及仰拱累积损伤计算方法，并得到引起仰拱混凝土损伤破坏的静载力阀值。进行对不同静载条件下仰拱混凝土损伤演化规律的对比分析，给出不同工况及不同阶段损伤演化趋势的定量表达式，探明混凝土试件损伤主要分布在中间受拉区域，底部损伤值相对较大并最终发生破坏。

累积特征；仰拱混凝土；循环荷载；静载

铁路隧道仰拱作为隧道底部衬砌结构，一方面承受轨道板、混凝土板、CA砂浆和填充层等因自重引起的荷载，另一方面承受列车激振荷载。我国隧道仰拱设计时只能凭借经验选取结构形式和设计参数。现行的《公路隧道设计规范》和《铁路隧道设计规范》未给出仰拱结构累积损伤的计算方法。在列车大重量、高密度的运营条件下，使轨下基础承受更大的振动荷载，使得线路状态和轨道结构及底部结构破坏特征较传统线路变化明显[1-2]。隧道底部结构承受围岩压力和列车振动荷载的作用，然而轴重的提高直接引起动载幅值的增大，当动载幅值并达到一定量值，进而产生隧底结构累积损伤。隧底结构的受力状态直接影响到整个隧道结构的安全稳定[3-4]。基于连续损伤力学，国内外学者建立了多种考虑静载及动载作用混凝土损伤模型[5],用于描述静载及动载引起混凝土损伤的研究未考虑不同动载幅值影响，并且对于混凝土构件损伤特征的一般仅给出经验公式。早期研究学者如Aas-Jakobsenp，Tepfers，Hsn，Holmen和Cornelissen等，主要通过试验得到疲劳寿命曲线，并得到广泛应用。但上述模型不能很好地表征静载和动载耦合作用下隧底结构混凝土的累积损伤规律。Hsu, van Leeuwen 和 Siemes, Tepfers 和 Kutti, Weigler和 Klausen 等进行了循环荷载作用下混凝土单轴拉压试验研究，提出了疲劳寿命曲线并加以改进，并进行损伤量与物理量之间的关系探讨。然而，上述研究经验模型不能准确描述混凝土损伤寿命预测和损伤的整个过程。依据混凝土累积损伤理论，开展不同静载条件下动静载作用混凝土损伤特征的试验研究。对仰拱混凝土累积损伤演化规律、分布特征及发展规律进行分析，给出满足隧底力学环境条件混凝土损伤计算方法。

1　累积损伤模型

1.1 混凝土损伤模型

研究采用的损伤模型为Helmholtz各向同性标量模型，并参考了Saanouni-Forster-Hatira损伤模型提出的“总自由能等效原理”[6]，主要描述材料损伤变化过程中损伤演化及性能退化的非线性关系。

(1)

式中：ψe为材料未损伤部分的自由能；ψp为材料损伤部分自由能；κ为拉力或压力累积塑性应变变量；其中损伤变量D的定义AD和A的比值如下所示[7]：

(2)

混凝土损伤变量描述了内部裂纹扩展和损伤增量增加的过程，并参考了Saanouni-Forster-Hatira模型，给出了具体自由能方程表达式如下：

(3)

式中：λ和μ均为无损材料的Lame常数；ρ为自由能密度参数，从而得到应力应变的关系如下：

(4)

式中：λ和μ均为含损伤材料的Lame常数，且有：

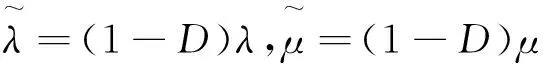
(5)

根据由能量释放率表征的损伤驱动力的损伤演化方程为：

(6)

损伤的判断准则表示为定义在损伤屈服面内的损伤演化规律，具体损伤屈服函数如下[8]：

(7)

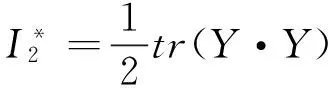
对隧道仰拱结构的内力分布规律以及结构破坏的原因等分析[9]，可知仰拱结构的破坏主要受拉应力引起。本文给出了循环荷载作用下损伤演化规律，损伤值主要考虑受动拉应力影响。为了得到损伤演化规律，给出了如下损伤加载条件：

1.2扩展到损伤累积

基于连续损伤力学，建立累积损伤预测方法，并进行混凝土损伤演化规律的研究。建立损伤变量与循环次数间的关系描述混凝土累积损伤发展过程，混凝土累积损伤变量需要满足以下条件：

1)初始条件下单次循环荷载作用混凝土的损伤变量的确定；

2)循环荷载作用下每个循环次数所对应混凝土的损伤变量值；

3)满足混凝土破坏条件的损伤阀值。

(8)

(9)

式中：a,b,s和φ为模型参数。

将公式(9)和公式(12)代入公式(11)可以得到：

(10)

通过以上公式对于累积损伤模型的推导，给出了单次损伤变量的表达式如下[11]：

(11)

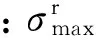
为了描述混凝土损伤演化过程，根据公式(8)给出循环荷载条件下混凝土损伤变量方程如下：

(12)

结合公式(13)，给出初始条件及混凝土损伤破坏条件下损伤变量的定义：

式中：N0是初始损伤条件下循环次数；Nf是疲劳破坏条件下循环次数；损伤破坏判断值为DcR=1。

循环荷载作用下混凝土循环次数Nf可以表示为：

(13)

为了建立考虑循环次数累积损伤计算模型，给出如下损伤演化方程：

(14)

1.3阻抗损伤指标

混凝土损伤是对材料内部微孔洞和微裂缝等缺陷的表征，微缺陷的发展导致材料有效面积的减少。损伤力学将微缺陷区域视为局部均匀场，通过宏观损伤变量来反应结构微裂纹局部均匀场的整体效应。目前，现代测试方法通过获得的机电信号进行数学处理，对损伤状态的量化仍在研究和发展。

基于机电耦合阻抗法EMI(Electromechanical Impedance Method)方法的健康监测则需要一个统计指标来衡量损伤前后PZT传感器电信号的变化程度。更多的学者选择采用Giurgiutiu和Rogers于1998年提出的结构健康和损伤2种状态信号的均方根指数RMSD (Root Mean-square Deviation)作为适合的损伤指标，形式如下:

(15)

由于导纳(或阻抗)信号是复数形式，其实部(电导A)和虚部(电纳B)相应的损伤指标可分别表示为:

(16)

(17)式中，xi和yi(i=1, 2, 3, …, n)为结构发生损伤前后PZT片导纳(或阻抗)值。实际结构的检测中，往往选择导纳或阻抗的实部作为测量损伤指标[12]。

2　试件制备及试验方案

为了准确的获取动力荷载作用下混凝土损伤性能的演化规律，进行了大量混凝土试验研究。试验主要研究动静荷载耦合作用下混凝土累积损伤特征，具体分析步骤如下：

1)试件包括2种尺寸100 mm×100 mm×100 mm和100 mm×100 mm×300 mm，在24 h内完成混凝土浇筑、成型及拆模的工作，最后在混凝土养护室内进行28 d标准养护。

2)分别进行混凝土试块静力加载测试和无损检测：采用立方体试块进行混凝土静载试验获取抗压强度、弹性模量和泊松比；采用ETM (Emodumete -TM) 进行长方体试块无损检测，得到动弹性模量、动剪切模量等动态力学参数。

3)荷载主要包括侧向静载、竖向静载和动力荷载3种荷载共同作用试块，具体加载方案为：首次在试块两侧施加2 kN侧向加载力，其次逐步施加竖向静力荷载且加载到荷载水平，进而进行不同加载力幅值的施加。

2.1试件制备及混凝土参数

进行混凝土不同参数的测定及试验研究，同时浇筑2种尺寸混凝土试块，采用塑料模具成型及24 h后拆模，并在混凝土养护室内进行28 d标准养护。水泥材料选用湖南水泥厂生产的等级为42.5的普通波兰水泥，采用的粉煤灰产于湖南湘潭发电厂。试验中细骨料的细度模数为2.7及表观密度为2.67 kg/m3，粗骨料采用粒径为5～25 mm的石灰岩碎石。混凝土试件设计的强度为C35，具体混凝土配合比见表1。

为了得到混凝土相关动态力学参数和静力力学参数，进行试块前期测定试验。分别进行立方体(100 mm×100 mm×100 mm)静力试验并得到抗压强度等静力参数，采用ETM(Emodumeter-TM)对长方体(100 mm×100 mm×300 mm)进行无损检测得到动弹性模量、动剪切模量等相关动态力学参数如表2所示。

表1　混凝土配合比及耐久性指标Table 1 Mix proportions of concrete and durability indicators

表2　混凝土动静态力学参数Table 2 Dynamic mechanical parameters and compressive strength

2.2仰拱力学环境模拟方法

仰拱结构受力主要受由围岩压力产生的静载和由列车荷载引起的动载共同作用如图1(a)所示。在仰拱中选取局部区域进行损伤特征研究如图1(b)所示，并对于所选取的构件周围施加仰拱力学环境，进而准确模拟仰拱结构受力及损伤演化特征。

为了准确地模拟隧道长期列车荷载作用下隧底结构所受力学环境，采用自制静力加载装置图2(b)和MTS动力加载设备图2(a)进行混凝土试验。自制装置主要由接触钢板、接触弹簧、液压千斤顶和模型箱等部分组成所示。通过液压千斤顶和侧向接触弹簧对试块施加静载，模拟由围岩压力引起的隧道仰拱结构的压力作用。根据刚度相似比原理，通过测定刚度的弹簧接触试块模拟衬砌与围岩之间的接触关系。通过MTS系统提供一定频率和加载力幅值的正弦荷载。

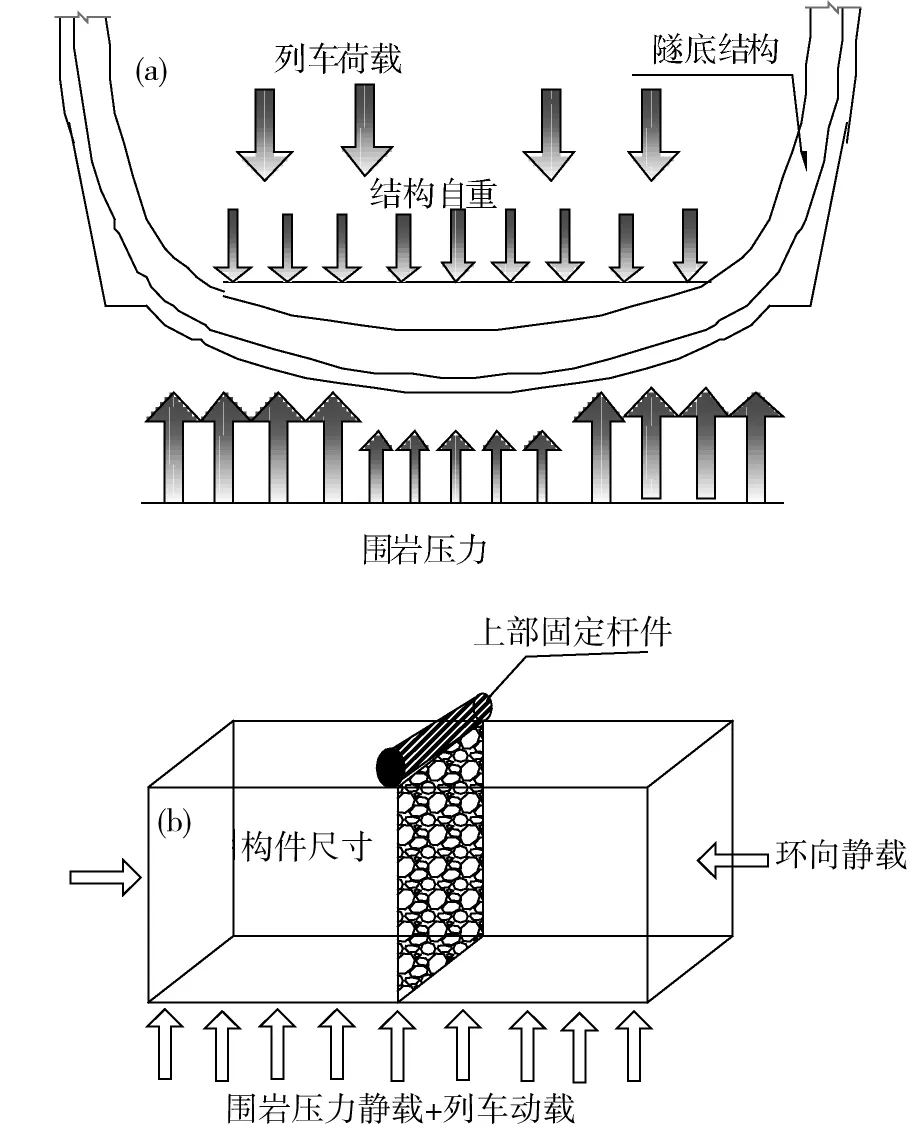
(a)隧底结构受力环境；(b)仰拱试件受力示意图图1　隧底结构受力及加载示意图Fig.1 Fatigue loading curve

(a)MTS动力系统；(b)自制装置图2　MTS系统和自制装置Fig.2 Self-developed experimental devices

2.3损伤监测方法

混凝土损伤监测方法需要能够解决动载作用下材料损伤探测与采集的问题[13]。传感器采用压电陶瓷片进行混凝土材料损伤探测、强度预测、损伤评估及其健康检测[14-15]，其中PZT压电陶瓷片(piezoelectric lead zirconate titanate) 黏贴于试块表面中间见图3(b)所示。运用PV80A设备采集传感器不同频段的机电信号，通过信号换算进而得到混凝土内部损伤量， 试验数据采集系统见图3所示。

(a)数据采集系统；(b)试块测点图3　数据采集系统和试块测定Fig.3 Data acquisition systems and monitoring points

2.4试验方案设计

对静载荷和动载荷耦合作用下仰拱试块损伤性能的演化规律进行研究。其中，动荷载振动频率为12 Hz，并采用振动幅值160 kPa的正弦加载曲线；依据隧道仰拱数值计算结果，选取了侧向静载力2 MPa。

为了研究不同静载力水平下循环荷载作用引起的仰拱混凝土损伤、性能衰减及破坏整个过程变化。试验加载步骤主要分以下几个方面：

1) 为了模拟隧道上部围岩压力引起衬砌结构环向压力，首先在试件侧向施加额定静载力。

2)其次，通过MTS系统施加额定静载力模拟隧底底部围岩压力。

3)最后，通过MTS系统施加循环荷载并展开对混凝土试件损伤破坏全过程的试验研究。

由于混凝土试验结果存在较大的离散型，为了在相同标尺坐标系下进行不同工况的比较，采用比值形式的变量进行实验结果分析。静载阶段试验数据的分析，采用施加荷载F与破坏荷载Fu的比值为自变量研究混凝土累积损伤演化规律。根据混凝土静载试验数据，得到破坏荷载经验计算公式为:Fu=0.2×fc×A,

其中：fc为混凝土抗压强度；A为抗压面积。

荷载水平主要反应围压静载作用，依据长方体试块静力破坏试验数据及数值计算结果，本文选取4种不同的荷载水平。通过静载与破坏荷载的比值表示4种工况的竖向加载条件：

工况1：竖向静载力为0.70×Fu，振幅160 kPa；

工况2：竖向静载力为0.75×Fu，振幅160 kPa；

工况3：竖向静载力为0.80×Fu，振幅160 kPa；

工况4：竖向静载力为0.85×Fu，振幅160 kPa。

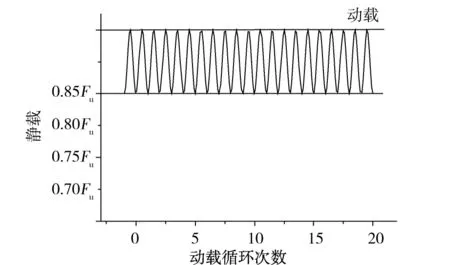
图4　隧底结构受力及加载示意图Fig.4 Fatigue loading curve

3　仰拱混凝土试验结果与分析

主要研究不同静载条件下，静载与动载荷载共同作用引起的仰拱损伤、性能衰减及破坏整个过程变化。分析不同静力水平条件下，循环荷载引起混凝土试件损伤破坏及性能衰减规律。通过对试验数据的公式拟合并确定相关参数，进行仰拱混凝土全过程损伤演化及累积应变规律的量化分析。

3.1不同静载仰拱混凝土损伤特征研究

进行仰拱试件静力加载破坏过程损伤演化及性能衰减规律的研究。通过逐步施加静载，试验得到随着荷载水平提高仰拱混凝土累积损伤曲线如图5(a)所示。结果表明：随着荷载水平逐渐增大，在[0,0.75Fu]范围内损伤量逐渐增大，损伤值逐渐增大到0.5；荷载水平在[0.75Fu,1]范围内损伤量增长速率明显变快，表现出明显的非线性特征并快速破坏阶段。

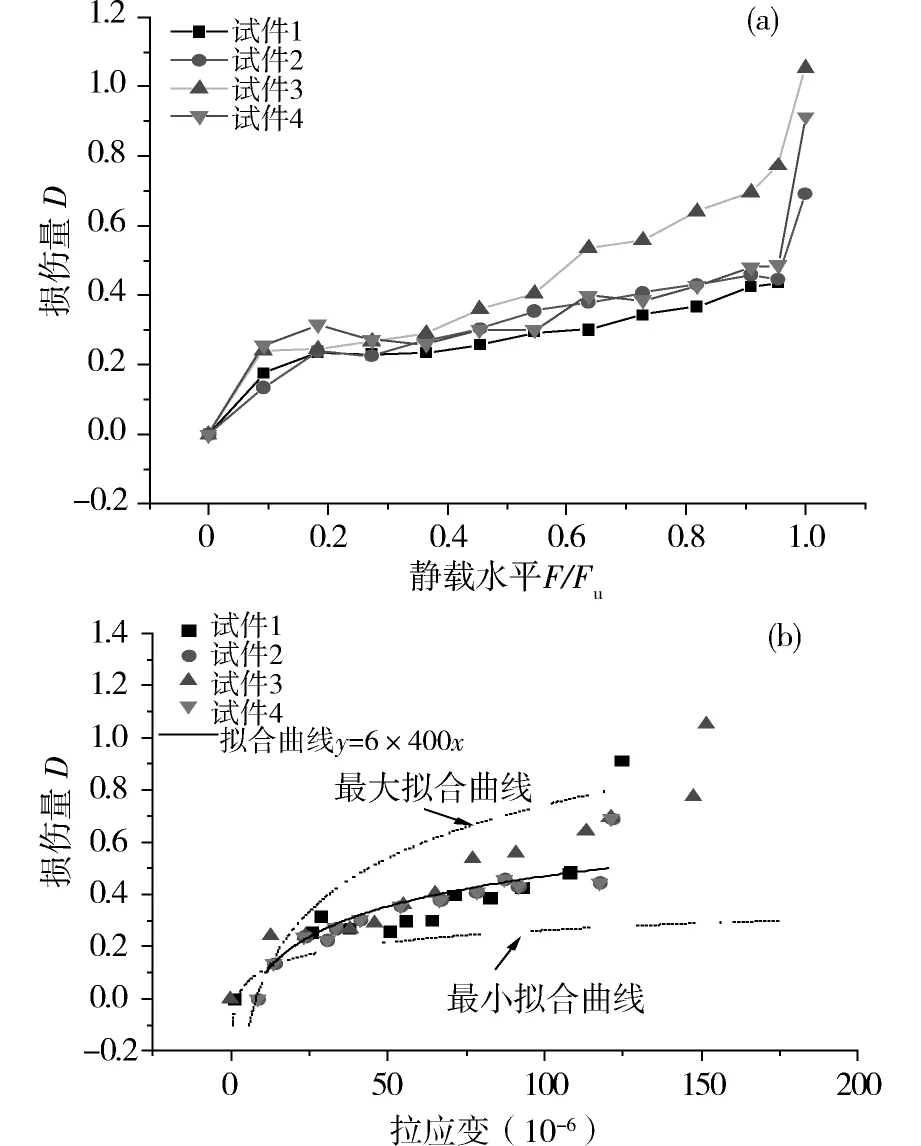
(a)静载损伤曲线；(b)损伤应变曲线图5　损伤变化曲线Fig.5 Change of damage variable curves

根据混凝土应变分析可知，拉应变是引起材料性能衰减及破坏的主要影响因素。根据拉应变和损伤变量的关系如图5(b)所示，可得随着荷载水平的提高，损伤值逐渐增大；随着拉应变的增大，损伤值逐渐增大。结合试验给出了拉应力和损伤量之间关系曲线，基于ABAQUS/Explicit数值计算平台，开展仰拱混凝土损伤特征的数值计算研究。

3.2仰拱混凝土累积损伤特征研究

给出了不同静载损伤变量和循环次数的数据曲线，以及相应损伤演化公式的拟合曲线。如图6(a)所示，竖向静载力为0.7Fu条件下损伤演化曲线存在两个发展阶段：初期增长阶段和稳定发展阶段。在工况1条件下随着循环次数的增加，累积损伤演化曲线最终趋于稳定。

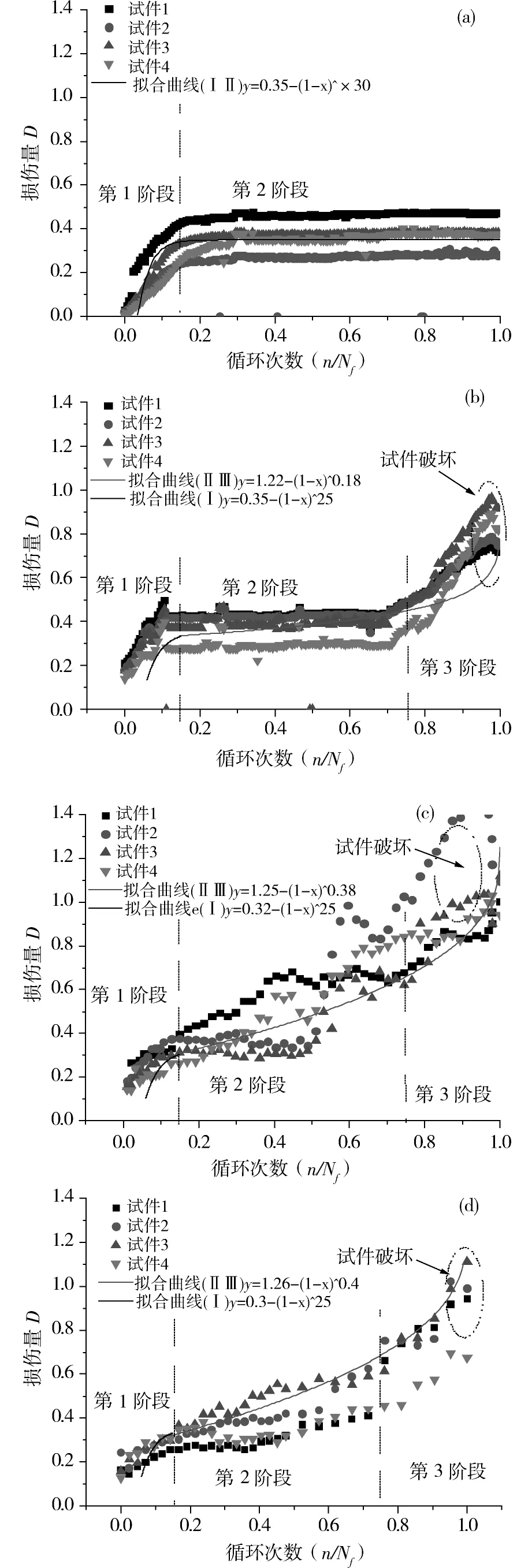
(a)工况1；(b)工况2；(c)工况3；(b)工况4图6　不同荷载水平下混凝土损伤变化曲线Fig.6 Curve of damage variable and cyclic fraction

根据图6(b)，6(c)和6(d)所示， 对比不同荷载水平下混凝土损伤变化曲线可得：在荷载水平小于0.70Fu时，随着循环比值的增大，损伤变量逐渐趋于损伤值约0.6且未发生混凝土破坏。其他荷载水平条件下，随着荷载水平的提高，损伤值的变化速率增大且最终发生混凝土破坏。

根据试验损伤演化曲线，可以将该曲线分为3个阶段：1)初期增长阶段；2)稳定增长阶段；3)快速发展阶段。第1阶段次数比值范围[0 0.15],当增长损伤值达到0.3进入第2阶段稳定增长，最后损伤值达到0.7时进入第3阶段，增长速率明显提高并最终发生混凝土破坏。

最后给出损伤变量和次数比的非线性关系，根据拟合公式和试验数据较好的一致性，提出适用于循环荷载作用下隧底结果混凝土的累积损伤计算公式：

(18)

根据表3累积损伤公式拟合参数，进行不同荷载水平下损伤变量的量化计算研究。公式中参数τ和参数θ用于控制损伤值及其变化趋势。当τ>1时，θ增大伴随损伤值增长率的增大；当τ<1时，θ减小伴随损伤值增长率的增大。

在初始增长阶段，θ由30变为25，表明在0.7Fu荷载条件下损伤值增长率小于其他工况条件下增长率。在稳定增长阶段及快速增长阶段，对比存在破坏阶段的荷载条件(0.75Fu，0.80Fu和0.85Fu)可得：θ由1.22变化到1.26，损伤值增长率逐渐提高，表明混凝土试块加速破坏。综上所述，荷载水平对于隧底结构混凝土有重要影响。

表3　累积损伤方程拟合参数Table 3 Analysis of claims data

3.3数值计算对试验数据的验证与对比分析

基于ABAQUS/Explicit数值计算平台，并结合试验给出了拉应力和损伤量之间关系曲线,混凝土损伤及破坏全过程中损伤演化曲线和损伤分布特征。首先结合表3和式(18)给出拟合曲线，然后提取数值计算结果曲线进行对比，如图7所示。对工况1中第1阶段和第2阶段损伤数值计算数据与理论拟合曲线对比和其他工况第2阶段和第3阶段对比。通过数值计算和实验拟合曲线进行对比，具有较好的一致性，相互验证了混凝土损伤阶段及损伤发展规律。

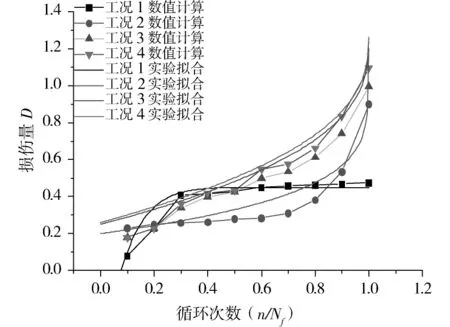
图7　不同静载混凝土损伤变化曲线Fig.7 Curves of damage variable and cyclic fraction

图8　不同荷载水平下混凝土损伤变化曲线Fig.8 Curves of damage variable and cyclic fraction

图8为损伤分布云图和混凝土试验图片的对比。从损伤分布云图可以看出：初始阶段损伤发生在混凝土试块中底部；随着损伤值的增大，损伤由下部逐渐向上发展且底部损伤值增大。

对于第1阶段和第2阶段前半段，即损伤值在[0,0.6]范围内混凝土试件表面为发现肉眼可见裂缝或其他损伤现象。损伤发展进入第3阶段，即损伤值达到0.75，在试件中间区域出现微裂缝并发生破坏。通过对3阶段的对比，数值计算模型能够模拟混凝土整个损伤过程包括损伤位置、损伤程度和损伤方向。

4　结论

1)根据混凝土加载全过程损伤演化试验曲线，研究累积损伤非线性增长特征。得到损伤值与循环次数比值的关系曲线并得到3阶段的损伤演化规律。

2)对比分析不同静载仰拱混凝土动力试验数据，得到影响混凝土损伤快速发展并发生破坏的损伤阀值，并得到损伤方程的相关参数并对损伤演化进行了量化分析。

3)数值计算结果得到初始损伤发生位置、损伤发展方向、损伤程度及其演化规律，并验证了损伤演化规律和损伤分布。

[1] 王春景，雷明锋，彭立敏. 病害隧道结构安全性评价模型与方法[J].铁道科学与工程学报,2011,8(3):73-77.

WANG Chunjing，LEI Mingfeng，PENG Limin. Safety evaluation model and method of tunnel disease sturcture [J]. Journal of Railway Science and Engineering, 2010,8(3) : 73-77.

[2] 丁祖德，彭立敏，雷明锋,等.高速铁路隧道列车振动响应影响因素分析[J].铁道科学与工程学报,2011,8(4):1-6.

DING Zu-de, PENG Limin, LEI Mingfeng, et al. nalysis of influence factors on dynamic response of high-speed railway tunnel under vibration load [J]. Journal of Railway Science and Engineering, 2011,8(4): 1-6.

[3] 李玉峰，彭立敏，雷明锋,等. 交叉隧道工程设计施工技术研究进展[J].铁道科学与工程学报,2014,11(1):67-73.

LI Yufeng, PENG Limin, LEI Mingfeng, et al. Research progress in the design and construction technology of crossing tunnels [J]. Journal of Railway Science and Engineering,2014,11(1): 67-73.

[4] 康立鹏，施成华，彭立敏,等. 基于正交试验的立体交叉隧道施工影响因素研究[J].铁道科学与工程学报,2012,9(4):70-74.

KANG Lipeng，SHI Chenghua，PENG Limin, et al. Study on the influence factors of crossing tunnel based on orthogonal experiment [J]. Journal of Railway Science and Engineering,2012,9(4): 70-74.

[5] Ngoc-Anh Do , Daniel Dias, Pierpaolo Oreste, et al. 2D numerical investigation of segmental tunnel lining behavior[J].Tunneling and Underground Space Technology, 2013,37(6): 115-127.

[6] Sannouni K, Forster C, Hatira F B. On the anelastic flow with damage[J]. Int J DamaMech,1994,3(1):140-169.

[7] Rashid K, Abu Al-Rub, Sun-Myung Kim. Computational applications of a coupled plasticity-damage constitutive model for simulating plain concrete fracture[J]. Engineering Fracture Mechanics, 2010(77):1577-1603.

[8] Cicekli U, Voyiadjis G Z, Abu Al-Rub R K. A plastic and anisotropic damage model for plain concrete[J]. International Journal Plasticity 2007, 23(0):1874-900.

[9] 施成华，彭立敏，王伟. 铁路隧道仰拱破坏力学形态的试验研究[J]. 实验力学,2005，20(1)：57-64.

SHI Chenghua, PENG Limin, WANG Wei. An experimental study on mechanics pattern of bed disease in railway tunnel[J]. Journal of Experimental Mechanic, 2005,20(1)：57-64.

[10] Chaboche J L, Lesne P M. A non-linear continuous fatigue damage model[J]. Fatigue and Fracture of Engineering Materials and Structures, 1988，11(1):1-7.

[11] 杨晓华，姚卫星，段成美. 确定性损伤累积损伤理论进展[J] 中国工程科学, 2003,5(4): 81-87.

YANG Xiaohua, YAO Weixing, DUAN Chengmei. The review of ascertaiable fatigue cumulative damage rule [J]. Engineering Science, 2003,5(4): 81-87.

[12] Park G, Sohn H, Farrar C R, et al. Overview of piezoelectric impedance-based health monitoring and path forward[J]. The Shock and Vibration Digest, 2003, 35(6): 451-463.

[13] Dansheng Wang, Hongyuan Song, Hongping Zhu. Numerical and experimental studies on damage detection of a concrete beam based on PZT admittances and correlation coefficient[J]. Construction and Building Materials, 2013, 49：564-574.

[14] Soh C K, Bhalla S. Calibration of piezo-impedance transducers for strength prediction and damage assessment of concrete[J]. Smart Mater Struct ,2005,14(4):671-684.

[15] WANG Dansheng, ZHU Hongping. Monitoring of the strength gain of concrete using embedded PZT impedance transducer[J]. Construction and Building Materials , 2011(25):3703-3708.

Experimental study on static and dynamic load forcumulate damage characteristics of tunnel invert concrete

LIU Ning, PENG Limin, SHI Chenghua

(School of Civil and Engineering,Central South University, Changsha 410075, China)

Common actions of surrounding rock pressure and dynamic loading affects the service life of tunnel invert. However, the relevant theories research on accumulate damage behavior causing by static and dynamic loading are still limited and not included in current design codes. The experimental research presents a accumulate damage mode for describing the damage behavior of invert concrete due to static and cyclic load in tunnel environments. On the one hand, the damage model is already validated and the damage calculating method is obtained. On the other hand, this paper presented the threshold of the critical static load level causing the failure of the specimen. Moreover, comparison of the different static load level causing the damage of the specimen and the quantitative expression of the damage process is presented in this paper. The evolution of initial damages appeared first at the bottom centre of specimen and new damages will then form upward progressively.

damage characteristics; invert concrete; cyclic load; static load level

2016-02-29

国家自然科学基金煤炭联合基金资助项目(U1361204)；国家自然科学基金资助项目(51278494)

施成华(1973-)，男，安徽黄山人，教授，从事隧道与地下工程研究；E-mail：csuch@163.com

U25

A

1672-7029(2016)10-1977-08