考虑主塔刚度影响的三塔斜拉桥振动基频实用公式

陈恒大，邬晓光，姚丝思，郭飞,2

(1.长安大学 桥梁与隧道陕西省重点实验室，陕西 西安 710064；2.浙江省交通规划设计研究院，浙江 杭州 310000)



考虑主塔刚度影响的三塔斜拉桥振动基频实用公式

陈恒大1，邬晓光1，姚丝思1，郭飞1,2

(1.长安大学 桥梁与隧道陕西省重点实验室，陕西 西安 710064；2.浙江省交通规划设计研究院，浙江 杭州 310000)

为方便计算多塔斜拉桥的竖向自振频率，基于最简单的多塔斜拉桥形式——三塔斜拉桥，考虑主塔刚度对振动频率的影响，应用Rayleigh法，给出主梁竖向自由振动的振型函数和主塔纵向自由振动的振型函数，并推导出考虑主塔刚度影响的三塔斜拉桥竖弯振动频率公式，且对其精确性进行多个算例验证。研究结果表明：主塔刚度对于三塔斜拉桥竖弯刚度影响较大，频率计算时应予以考虑，给出的能量法得到的纵飘基频计算值与有限元值误差比规范解与有限元值误差小，该公式能满足概念设计阶段的要求，适用于三塔斜拉桥的振动基频估算。

桥梁工程 ；三塔斜拉桥；主塔刚度；基频；实用公式

随着桥梁结构形式的多样化，三塔斜拉桥应运而生，相比传统独塔或双塔斜拉桥，三塔斜拉桥的中间塔两侧既没有辅助墩和过渡墩，又没有端锚索，缺少了对主梁和索塔刚度的有效帮助，使已经是柔性结构的斜拉桥柔性更大[1-4]。因此，对独塔或双塔斜拉桥在概念设计阶段的动力特性估算由于忽略了主塔刚度的影响而不适用于三塔斜拉桥。《公路桥梁抗风设计规范》中的双塔斜拉桥的基频估算公式是以双塔漂浮体系为基础，找出影响斜拉桥的振动特性的主要设计参数，根据现有斜拉桥振动特性资料进行回归分析或者曲线拟合，由于统计样本在数量及规格上的不足，大跨度、超大跨度斜拉桥估算频率值与真实频率值存在较大差异[5-8]；李国豪等〗[9]将斜拉桥看作一种在纵向稍作浮动的弹性支承连续梁，提出单质点振子模型估算漂浮体系斜拉桥的1阶频率，需要将桥面质量及塔架自重等效换算后堆聚塔顶存在误差较大的问题；袁万城等[10]针对文献[9]单质点模型计算精度不足的缺陷，采用分开考虑主塔、主梁的双质点振动模型，提高了漂浮体系斜拉桥基本周期的估算精度；张杨永[11]根据主塔塔顶的抗推刚度与主梁的等效摆动刚度的差异，对文献[10]提出的估算公式进行修正；柳惠芬[12]将漂浮体系斜拉桥比拟为多跨连续弹性地基梁，利用Rayleigh法给出了漂浮体系斜拉桥1阶竖弯频率近似计算公式；Walther[13]同样是将斜拉桥简化成多跨连续弹性地基梁模型，并对其进行修正；苗家武[14]考虑了斜拉桥主塔偏位对竖弯基频的影响，对文献[12～13]提出的估算公式进行完善和修正；盛善定等[15-16]等采用Rayleigh法推导了单跨悬索桥的近似竖弯基频表达式；王本劲等[17-21]采用Rayleigh法针对多塔悬索桥的竖弯振动频率进行了推导，并提出了精度较高的修正公式。综上所述，独塔、双塔漂浮体系的斜拉桥已有相关的竖弯基频近似计算公式，但是在诸多文献中均未对多塔斜拉桥的竖弯基频近似计算公式进行相关讨论，又由于多塔斜拉桥中间塔两侧无辅助墩、过渡墩和端锚索的帮助，柔度更大的多塔斜拉结构对主塔刚度提出了更高的要求，对该结构形式的竖弯基频还停留在定性认识阶段，对其定量计算公式几乎处于盲区。虽然通过有限元数值模拟和实验室现场振动实验可以获得其自振频率的分析结果，但只要结构体系某一参数改变，需重新建模分析，不利于桥梁技术人员在概念设计阶段快速判断桥梁结构的振动特性。为此，本文以多塔斜拉桥中的最简单形式——三塔斜拉桥为例进行振动基频研究，采用Rayleigh法推导其竖弯基频估算实用公式供初步概念设计，亦可对施工图设计阶段计算机的分析结果进行校核。

1　基于Rayleigh法计算振动频率

当系统进行固有振动时，如果不考虑阻尼力消耗能量，其动能和势能会反复交换，对于保守系统，其结构总能量是守恒的。可知，频率ωb的近似公式为

(1)

式中：ωb为与此对应的频率；ωbb为不考虑主塔刚度时频率；EI(x)为弯曲刚度；m(x)为质量分布值；φ(x)为满足桥梁位移边界条件的近似振型函数。

为方便表述，对下文中的符号作如下说明：EGIG和ETIT为加劲梁、主塔的抗弯刚度；η，ξ和ηci为加劲梁、主塔及拉索的振型函数；mG，mT和mci为加劲梁、主塔及拉索的线均布质量；Eci和Aci为拉索的弹性模量及截面面积；αci和Lci为拉索的水平倾角及长度。

目前，大跨度斜拉桥多采用自锚式漂浮体系，塔墩固结、塔梁分离，塔墩上设置竖向支承(半漂浮)或者不设置竖向支承(全漂浮)。作基本假定如下：

1)斜拉桥视为平面结构，结构变形符合线弹性的假定，适用叠加原理；

2)斜拉索视为一根直杆，不考虑弹性模量的修正；

3)不考虑主梁、主塔的Ρ-Δ效应；

4)不考虑斜拉桥各部件受力后几何尺寸的改变所引起的结构内力重分配。

1.1结构体系的势能

斜拉体系在铅垂平面内发生1阶竖向振动时，其势能为加劲梁、主塔(中间主塔及边塔)和拉索势能之和。

加劲梁的势能为

(2)

主塔的势能为

(3)

图1　拉索与主梁的变形协调Fig.1 Deformation compatibility of cable and main girder

(4)

由于整体结构的体系的振动，使得拉索的倾角发生变化，索力也发生变化，索力的垂直分量的变化量为ΔFv≅ΔF·cosα·dα，

则拉索二次势能为

(5)

于是，整个斜拉体系的势能为：

(6)

1.2结构体系的动能

斜拉体系在铅垂平面内发生1阶竖向振动时，其动能为加劲梁、斜拉索和主塔动能之和。

加劲梁的动能为

(7)

斜拉索的动能为

(8)

主塔的动能为

(9)

则整个斜拉体系的动能为

(10)

1.3斜拉体系的竖弯基频

将式(6)、式(10)代入式(1)，可得到斜拉体系的竖向振动频率的计算公式为：

(11)

李国豪在文献[9]中指出，斜拉体系的面内弯曲振动的势能主要是由拉索的势能和主塔的势能，加劲梁势能及拉索的二次变形能是次要的，可以忽略不计。结构动能中，主梁和主塔的动能是主要的；拉索的动能可以忽略，亦不考虑系统阻尼对结构振动特性的影响。于是，该结构的竖弯频率理论近似公式：

(12)

由式(12)可知，基频ωb仅与结构的计算参数ET，Eci，Aci，IT，mG，mT和振型函数η(x，t)，ξ(z，t)有关，与斜拉索截面形式无关。求解三塔斜拉桥的振动基频，获得其基本振型函数η(x，t)和ξ(z，t)是前提。

而不考虑主塔刚度影响的结构竖弯频率理论近似公式为：

(13)

由式(13)可知，当不考虑主塔刚度影响时，基频ωbb仅与结构的计算参数Eci，Aci，MG和振型函数η(x，t)有关，与其他因素无关。

2　三塔斜拉桥竖弯基本振型

根据文献[9]及三塔斜拉桥的结构特点，可得到其1阶反对称和正对称的竖弯振型，如图2～3所示。

图2　1阶反对称竖弯振型Fig.2 Mode shape of 1st asymmetric vertical vibration

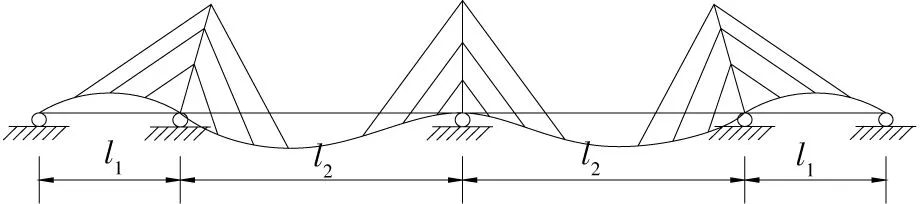
图3　 1阶正对称竖弯振型Fig.3 Mode shape of 1st symmetric vertical vibration

根据图2～3所显示的三塔斜拉桥1阶反对称和正对称竖弯振动变形图可知，其主梁振型函数η(x，t)与四跨连续梁竖向自由振动的振型函数η(x，t)类似。由于拉索和加劲梁满足变形协调条件，故只需确定满足边界条件的加劲梁的振型函数η(x，t)即可。而主塔振型函数ξ(z，t)与侧向受均布荷载作用下的悬臂塔的振型函数ξ(z，t)相似，由此只要找到能满足主梁竖向自由振动的振型函数η(x，t)和主塔纵向自由振动的振型函数ξ(z，t)，即可通过微积分运算求出三塔斜拉桥的1阶竖弯振动频率ωb，具体推导如下文。

3　1阶反对称竖向弯曲频率计算公式

加劲梁1阶反对称的振型关于中间支座反对称，如图4所示。

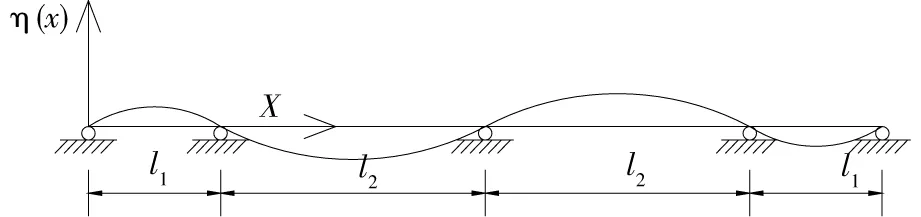
图4　加劲梁1阶反对称竖弯振型Fig.4 Mode shape of stiffening girder 1st asymmetric vertical vibration

主梁满足1阶反对称竖弯自由振动，设其满足边界条件的加劲梁振型函数为

(14)

(15)

(16)

(17)

由于加劲梁振型曲线在各桥塔处是连续的，即满足变形协调条件，可得

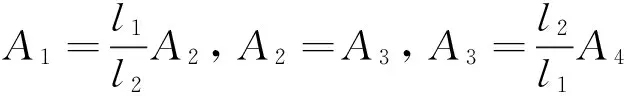
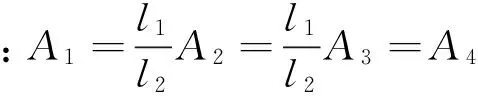
(18)

(19)

(20)

主塔满足1阶反对称竖弯自由振动，设其满足边界条件的主塔振型函数为

(21)

文献[11]中指出，结构竖弯平面内自由振动过程中，主塔塔顶顺桥向偏位为

Δh1=0.001 2l1，Δh2=0.001 2l2且Δh3=Δh1

(22)

(23)

将式(19)～(20)和式(22)～(23)代入式(12)可得：

(24)

不考虑主塔刚度时，同理可得：

(25)

4　1阶正对称竖向弯曲频率计算公式

加劲梁1阶正对称的振型关于中间支座对称，如图5所示。

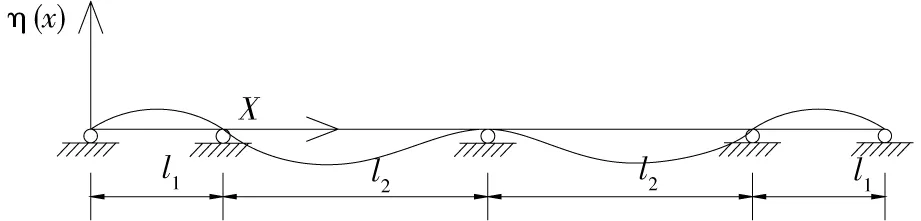
图5　加劲梁1阶正对称竖弯振型Fig.5 Mode shape of stiffening girder 1st symmetric vertical vibration

主梁满足1阶正对称竖弯自由振动，设其满足边界条件的加劲梁振型函数为

(26)

(27)

(28)

(29)

由于加劲梁振型曲线在各桥塔处是连续的，即满足变形协调条件，可得

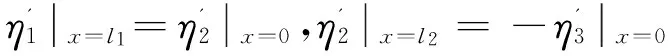
经简化可得

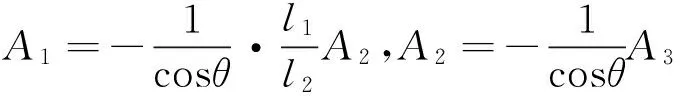
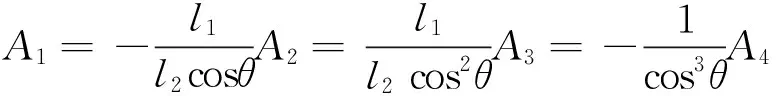
(30)

于是，可得：

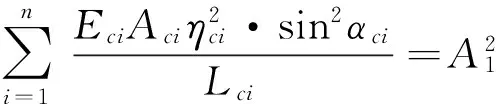
(31)

(32)

主塔满足1阶反对称竖弯自由振动，设其满足边界条件的主塔振型函数为

(33)

文献[11]中指出，结构竖弯平面内自由振动过程中，主塔塔顶顺桥向偏位为

Δh1=0.001 2l1，Δh2=0.001 2l2且Δh3=Δh1

(34)

(35)

将式(31)～(32)和式(34)～(35)代入式(12)可得：

(36)

不考虑主塔刚度时，同理可得：

(37)

5　算例验证

为验证文中解与有限元解的计算精度，选取4座三塔斜拉桥对上述公式加以验证，其中算例1，2和3均无辅助墩，算例4有辅助墩，实桥结构计算参数如表1所示。

详细计算结果如表2所示。

表1　实桥结构计算参数Table 1 Structural parameters of real bridge

表2　实桥1阶竖弯基频频率对比Table 2 First fundamental frequency of comparison vertical vibration

注：误差1是文中解2与有限元解之间的误差；误差2是规范解与有限元解之间的误差；误差3是文中解4与文中解2之间的误差

根据表1～2计算的数据分析可知，本文推导的考虑主塔刚度影响的三塔斜拉桥竖弯基频能量表达式与有限元数值结果误差1最大为5.71%，未考虑主塔刚度影响的公式解与有限元值误差会更大一些，而规范解与有限元解之间的误差2最大为13.79%，误差大小皆能满足概念设计阶段的要求；考虑了主塔刚度影响的频率公式计算值与不考虑主塔刚度影响的公式计算值相比精确度提高2%～5%，因此，在计算三塔斜拉桥竖弯基频时需考虑主塔刚度影响。1阶反对称的估算值与有限元值之间的误差比1阶正对称的估算值与有限元值之间的误差相对要大，原因在于其振型函数更趋近于简支固端梁的振型函数；本文推导的纵飘竖弯基频能量表达式仅适用于塔梁固结、墩支承的三塔斜拉桥的竖弯频率估算，不适用于其他斜拉体系的竖弯频率估算。

6　结论

1)推导了考虑主塔刚度和不考虑主塔刚度2种情形的基频计算公式，可知三塔斜拉桥竖弯基频随着主塔刚度的提升而增大，当考虑主塔刚度时，基频公式的计算精度提高2%～5%，因此在桥梁概念设计阶段振动基频计算时应充分考虑主塔刚度的影响。

2)三塔斜拉桥振动基频ωb仅与结构的计算参数主塔抗弯刚度、拉索弹性模量、拉索截面面积、主梁及主塔的线均布质量和主梁竖向自由振动的振型函数η(x，t)和主塔纵向自由振动的振型函数ξ(z，t)有关，与斜拉索截面形式无关。

3)通过假设主梁的基本振型函数，推导了其1阶竖弯正对称和反对称的能量表达式，给出的能量法纵飘基频计算值与有限元值误差比规范解与有限元值误差小约5%，此公式可以适用于考虑主塔刚度影响的三塔斜拉桥竖弯频率初步概念设计阶段的估算中。

4)竖弯频率实用计算公式仅适用于三塔斜拉体系，对其他体系斜拉桥应另做专门研究，《公路桥梁抗风设计规范》中的斜拉结构的竖向弯曲的基频估算公式不适用于塔梁固结、墩支承的三塔斜拉体系的竖弯频率的估算。

[1] Ge Y J, Xiang H F. Computational models and methods for aerodynamic flutter of long-span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10-11):1-13.

[2] Au F T K, Cheng Y S, Cheung Y K, et al. On the determination of natural frequencies and mode shapes of cable-stayed bridges[J]. Applied Mathematical Modelling, 2001(25):1099-1115.

[3] Nagal Masatsugu, Fujino Yozo, Yamaguchi Hiroki,et al. Feasibility of a 1,400 m span steel cable-stayed bridge[J]. Journal of Bridge Engineering.2004, 9(5):444-452.

[4] Cheung M X, Li D T, Lau W. Recent developments on computer bridge analysis and design[J]. Progress in Structural Engineering and Materials, 2000, 2(3):376-385.

[5] JTG/T D60—01—2004，公路桥梁抗风设计规范[S].

JTG/T D60—01—2004， Wind-resistant design specification for highway bridge[S].

[6] 刘春华，秦权．桥梁结构固有频率的统计特征[J]．中国公路学报，1997,10(4):49-54.

LIU Chunhua, QIN Quan. Statistics of natural frequencies for bridge structures[J]. China Journal of Highway and Transport, 1997,10(4):49-54.

[7] Zhang Yunfeng. The concept and development of smart structures technologies for long-span cable-supported bridges[J]. Marine Georesources and Geotechnology, 2003, 21(3-4):315-331.

[8] Brown Jeff L. Bridges: Hybrid span combines suspension, cable-stayed systems[J]. Civil Engineering, 2006, 76(9):16-17

[9] 李国豪．桥梁结构稳定与振动[M]．北京:中国铁道出版社，2002．

LI Guohao. Stability and vibration of bridge structures[M].Beijing: China Railway Publishing House，2002．

[10] 袁万城,闫冬.斜拉桥纵飘频率简化计算方法[J].同济大学学报(自然科学版),2005,33(11):1423-1427.

YUAN Wancheng, YAN Dong. Simplifiedcalculationalmethod of floating frequency for cable-stayed bridge [J]．Journal of Tongji university(Natural Science Edition), 2005,33(11):1423-1427.

[11] 张杨永.斜拉桥近似计算与结构体系研究[D]. 上海: 同济大学, 2010.

ZHANG Yangyong. Approximate calculation and study of structural system incable-stayed bridge [D].Shanghai :Tongji University, 2010.

[12] 柳惠芬.斜拉桥的实用简化分析[D]. 上海: 同济大学, 1995.

LIU Huifen. Approximate calculation and study of structural system incable-stayed bridge [D]. Shanghai :Tongji University, 1995.

[13] Walther R. Cable stayed bridge[M]. 2nd edition. American Society of Civil Engineer (Thomas Telford, Ltd.), 1999.

[14] 苗家武.超大跨斜拉桥设计理论研究[D]. 上海: 同济大学, 2006.

MIAO Jiawu. Study for design theories of suplongcable-stayed bridge [D]. Shanghai :Tongji University, 2006.

[15] 盛善定，袁万城，范立础．悬索桥振动基频的实用估算公式[J]．东北公路，1996( 1) : 71 -76．

SHENG Shanding，YUAN Wancheng，FAN Lichu． Practical estimation formula of vibration basic frequency of suspension bridge[J]． Northeast Highways，1996(1):71-76．

[16] 鞠小华，廖海黎，沈锐利．对悬索桥对称竖弯基频近似公式的修正[J]．土木工程学报，2002，2( 1) :44-49．

JU Xiaohua，LIAO Haili，SHEN Ruili． Modification on simplified formula of symmetric-vertical natural frequencies for suspension bridge[J]．China Civil Engineering Journal，2002，2 ( 1 ) : 44- 49．

[17] 王本劲，马如进，陈艾荣．多塔连跨悬索桥基频估算方法[J]．结构工程师，2011，27 ( 6) :54-58．

WANG Benjin，MA Rujin，CHEN Airong. Estimation of fundamental frequency of multi-pylon suspension bridge [J]．Structural Engineers，2011，27 ( 6) : 54-58．

[18] 王本劲,马如进,陈艾荣. 多塔连跨悬索桥基频估算实用公式[J].公路交通科技，2012,29(11):58-62.

WANG Benjin，MA Rujin，CHEN Airong． Practical formula of fundamental frequency estimation for multi-pylon suspension bridge[J]．Journal of Highway and Transportation Research and Development, 2012,29(11):58-62

[19] 张超，黄群君，许莉.考虑主塔刚度影响的三塔自锚式悬索桥竖弯频率计算公式[J].长安大学学报(自然科学版),2014,34(6):100-106.

ZHANG Chao, HUANG Qunjun, XU Li． Frequency formulas for vertical vibration of three-tower self-anchored suspension Bridge considering tower stiffness influence[J]．Journal of Chang’an University(Natural Science Edition), 2014,34(6):100-106.

[20] 姜洋.三塔悬索桥结构体系及施工过程关键问题研究[D]. 上海: 同济大学, 2014.

JIANG Yang. Study for structure system and process of construction for multi-tower suspensionbridge [D]. Shanghai :Tongji University, 2014.

[21] REN Weixin, PENG Xuelin, LIN Qinyou. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge[J]. Engineering Structures， 2005(27):535-548.

Practical vertical frequency formula for vibration of cable-stayedbridges with three tower considering tower stiffness influence

CHEN Hengda1,WU Xiaoguang1,YAO Sisi1, GUO Fei1,2

(1.Key Laboratory for Bridge and Tunnel of Shaanxi Province, Chang’an University , Xi’an 710064, China；2.ZHE JIANG Provincial Institute of Communications Planning, Design and Research, Hangzhou 310000, China；

In order to calculate fundamental frequency of the cable-stayed bridges with multi-tower conveniently, the cable-stayed bridges with three tower was taken as research object. Frequency formula for vibration mode of cable-stayed bridges was induced by the Rayleigh method and vibration mode function of vertical free vibration of main beam and vibration type function of longitudinal free vibration of main tower were introduced. The practical vertical frequency formula for vibration of cable-stayed bridges with three tower considering tower stiffness influence was then derived. Finally, the presented theoretical formula of fundamental frequency was found to be valid in engineering and the frequency formula for vibration was discussed therein. The results indicate that section types of the girder, tower and cable has no influence on the vertical frequency formula for vibration of cable-stayed bridges, but the tower stiffness has a great influence on vertical frequency of cable-stayed bridges. The constrain condition and tower stiffness should be carefully considered in the calculation of frequency. The fundamental frequency calculated by the recommended method has a smaller error compared with the finite element method (FEM) result, which satisfies the requirement of conceptive design. The presented theoretical formula can be applied to the estimation of frequency for vibration of cable-stayed bridges with three tower.

bridge engineering; cable-stayed bridges with three tower; tower stiffness; fundamental frequency; practical formula

2016-03-27

国家自然科学基金资助项目(51308056)；中国电力建设股份有限公司科技专项资金资助项目(2014-38)；中央高校基本科研业务费专项资金资助项目(201493212002)

陈恒大(1989-)，男，山东滕州人，博士研究生，从事大跨度桥梁结构理论分析与养护管理研究；E-mail：kuangyedeliusha@126.com

U441.3

A

1672-7029(2016)10-1962-08