二级边坡稳定性的三维分析

唐承铁，龙泽祥，许敬叔

(1.湖南省娄衡高速公路建设开发有限公司，湖南 衡阳 421000;2.中南大学 土木工程学院，湖南 长沙 410075)



二级边坡稳定性的三维分析

唐承铁1，龙泽祥2，许敬叔2

(1.湖南省娄衡高速公路建设开发有限公司，湖南 衡阳 421000;2.中南大学 土木工程学院，湖南 长沙 410075)

通过构建一个三维破坏机制，基于线性MC准则和极限分析法，对边坡高度H的解析解进行推导，采用“穷举法”进行优化计算，得到二级边坡的稳定系数，并与Michalowski的研究成果比较分析，从而验证解的有效性。研究结果表明：边坡的稳定系数不仅与倾斜角和内摩擦角有关，还与深度系数及宽高比有关。

二级边坡;三维破坏机构;线性MC准则;极限分析;穷举法

摩尔-库仑准则假设土体破坏时正应力和剪应力服从线性关系，被广泛应用于岩土工程的分析研究中。对于土质边坡的研究，土体的屈服曲线呈线性变化，因此MC准则是有效的。常见的稳定性方法有极限平衡法[1-2],极限分析法[3-5]等，相比于极限平衡法，极限分析法计算简单，是研究工程稳定性的一种有效方法[6-10]。极限分析法被大量的学者用来进行边坡的稳定性研究，不过，一般采用二维分析，三维分析比较少见。相比于三维分析，二维分析能更加保守的估计边坡的稳定性，然而在开挖宽度受到限制或斜坡开挖等情况时，利用三维分析，能更真实的反映边坡的实际破坏状态。采用极限分析对边坡稳定性进行三维分析时，破坏机构主要有以下2种，一种是三维多块体破坏机构，另一种是“牛角形”破坏机构。Michalowski[11]运用三维多块体破坏机构，该方法将三维滑坡体划分为一系列的块体，块体的速度场按二维情况构造，对滑坡的稳定性进行了研究。Farzaneh等[12]将三维多块体破坏机构应用于三维非均匀土坡的稳定分析中，探讨了采用迭代算法求最小上限解的方法。“牛角形”破坏机构是由Michalowski根据边坡的三维实际破坏形态提出，该破坏模式得到广泛的应用。Michalowski[13]在均质土体的破坏模式下，对孔隙水作用下二级边坡的稳定性进行了研究。Michalowski等[14]在三维“牛角形”破坏机制下，将地震荷载作为外荷载研究了边坡的稳定性。本文在Michalowski等研究成果的基础上，将“牛角形”破坏机构引入二级边坡的稳定性分析中。基于线性MC准则，运用极限分析上限法，分析讨论了边坡坡角、深度系数以及宽高比B/H等对稳定性系数的影响，对边坡工程的施工和加固，具有指导借鉴作用。

1　极限分析法的应用

极限分析法以塑性力学为基础，概念明确，计算简单，在边坡的稳定性研究中得到了广泛应用。利用极限分析法，分别计算求解破坏机制的外功率和内能耗散率，然后令二者相等，便可以得到边坡极限高度或顶部极限荷载的上限值。三维旋转破坏机制的总内能耗散D由2部分组成[14]，一部分是由体积变形引起的耗散DV，另一部分耗散Dt由速度间断面引起，其中DV和Dt分别通过下式计算：

(1)

Dt=∫StctvtdSt=∫StctvcosφdSt

(2)

总的内能耗散率D即为：

(3)

2　三维边坡临界高度上限解

2.1破坏机构的构建

构建顶点夹角为2φ，通过坡脚点D的圆锥形破坏机构，如图1所示。对称面上的轨迹线为?AD和?A'D'这2条对数螺旋线，AD的方程如下：

r=r0e(θ-θ0)tanφ

(4)

A'D'的方程为：

r'=r0'e-(θ-θ0)tanφ

(5)

其中：OA=r0；O'A'=r0'。圆锥形破坏机构的横截面为半径为R的圆，轴线到旋转中心O的距离为rm，则有：

(6)

(7)

f1和f2的表达式见文献[11，13～14]。

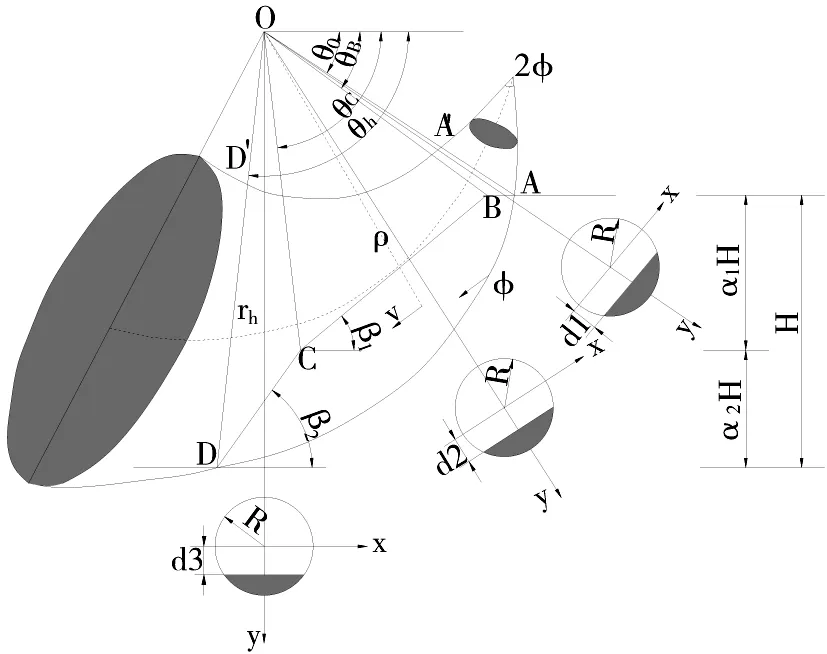
图1　三维旋转机制Fig.1 Three-dimensional rotational mechanism

当临界高度H取最小值时，该破坏机制的宽度B会是一个有限的数值，研究表明，临界高度H不仅与坡角、强度参数以及深度系数等有关，还与破坏机制的宽度有关。为了使边坡的破坏状态更加符合土体的实际破坏情况，在图1的中间嵌入一个宽度为b的块体，如图2所示。当b→时，得到与二维平面应变相同的解。

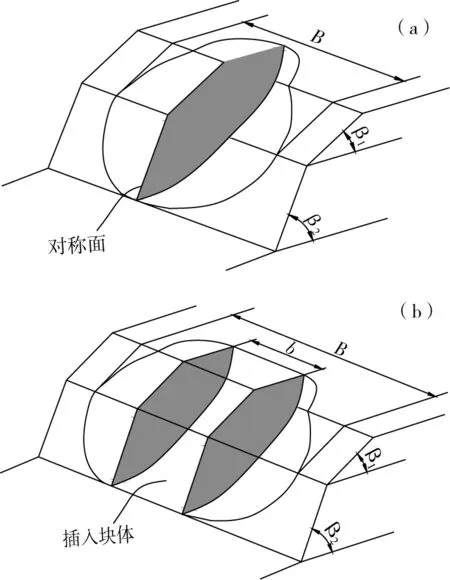
(a)三维旋转破坏机制；(b)块体插入机制图2　三维空间位置Fig.2 Three-dimensional space location

2.2外功率计算

破坏机制的总外功率由2部分组成，一部分是三维破坏机制本身的重力功率，另一部分是插入块体引起的重力功率。对于三维破坏机制，通过建立局部坐标系XOY，如图1所示，重力功率可表示为：

(8)

(9)

(10)

(11)

依据三角关系，θB和θC的表达式如下：

(12)

其中：k1=cosθ0-cosθhe(θh-θ0)tanφ-[α1cotβ1+α2cotβ2]H/r0

(13)

其中：k2=cosθ0-k1-α1Hcotβ1/r0

对式(8)中x和y的积分进行求解，对角度θ采用数值积分的方法计算，表达式(8)可改写成：

(14)

插入体的重力功率计算方法与二维情形的相同，但要在二维情形的结果上乘以插入体宽度b，其表达式为：

(15)

g1和g2表达式见文献[11，13～14]。

整个破坏机构的外功率为：

W=Wγ-insert+Wγ-3D

(16)

2.3内能耗散率计算

三维旋转机制的内能耗散包括坡面和坡顶面2个部分，由于为二级边坡，用DAB表示坡顶面的内能耗散，用DBC和DCD表示破面的内能耗散，其计算式分别为：

(17)

(18)

(19)

计算上式中对x的积分，采用数值积分法求解对角度θ的积分，因而，三维旋转机构的内能耗散为：

(20)

插入体的内能耗散计算方法与二维情形的相同，但要在二维情形的结果上乘以插入体宽度b，其表达式为：

(21)

g3和g4表达式见文献[11，13～14]，破坏机制的总内能耗散可表示为：

D=Dinsert+D3D

(22)

令破坏机制的总外功率与总内能耗散率相等，即W=D，通过化简可得出：

r0(g1+g2)γ=ctcotφ(g3+g4)

(23)

由几何关系有

(24)

根据式(23)～(24)，高度H的表达式为：

(25)

2.4优化计算

采用“穷举法”对高度H进行优化，通过使用嵌套的4个循环并依次改变循环变量θ0，θh，r0'/r0和b/H的值，来搜寻高度H的最小值，搜寻到的最小值，即为高度的一个上限解Hcr。循环变量需要满足以下条件：

(26)

其中：B'max为三维旋转破坏机构的最大宽度；B为边坡的限制宽度。

3　结果计算与分析

3.1对比讨论

线性MC准则下，边坡的稳定系数被定义为：

NL=γHc/c

(27)

根据极限分析上限法，在运动许可条件满足的情况下，破坏机构的最优解就是目标函数NL的最小值。为证明本文方法的正确性，在MC准则下，取内摩擦角φ=30°，并将求出的结果与Michalowski等[15]的结果进行比较分析。计算过程中，边坡倾角取β=45,60,75,90，边坡宽高比B/H取0.8,1.0,1.5,2.0,5.0,10.0。对比结果见表1。

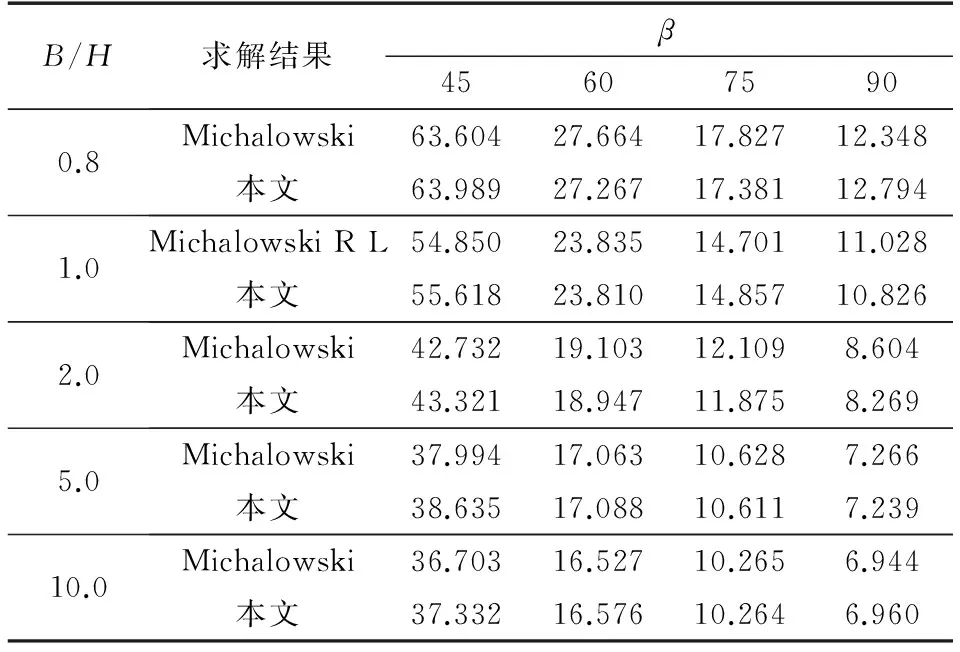
表1　本文方法与Michalowski(2009)方法的对比分析Table 1 Comparison with the solutions of Michalowski(2009)

3.2参数讨论

通过分别改变边坡上倾角β1，下倾角β2，内摩擦角φ和深度系数α1，研究各参数对土质边坡稳定性的影响，研究结果如图3～6所示。图3中，内摩擦角φ取10°,20°,25°和30°；图4中，深度系数α1取0.2,0.3,0.4和0.5；图5中，上倾角β1取30°,45°,60°和75°；图6中，下倾角β2取45°,60°,75°和90°。

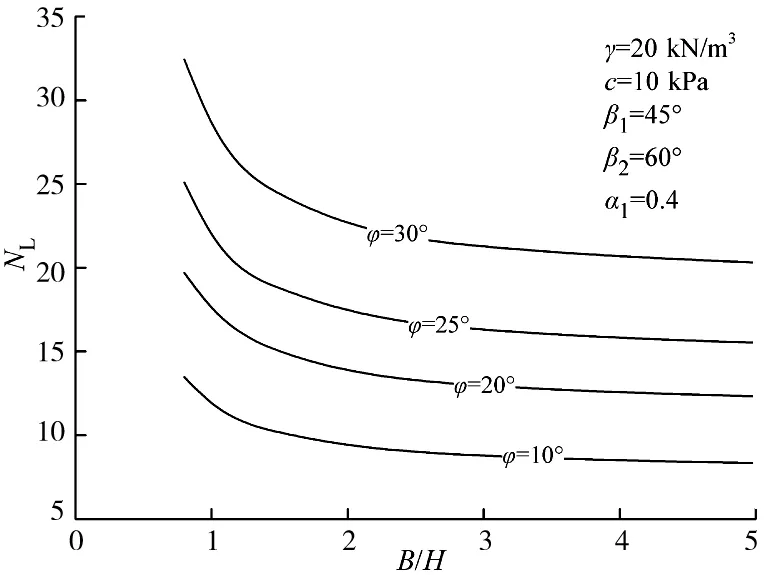
图3　内摩擦角φ与稳定系数NL的关系Fig.3 Relationships between friction angle φ and the stability factor NL

图4　深度系数α1与稳定系数NL的关系Fig.4 Relationships between the depth coefficient α1 and the stability factor NL

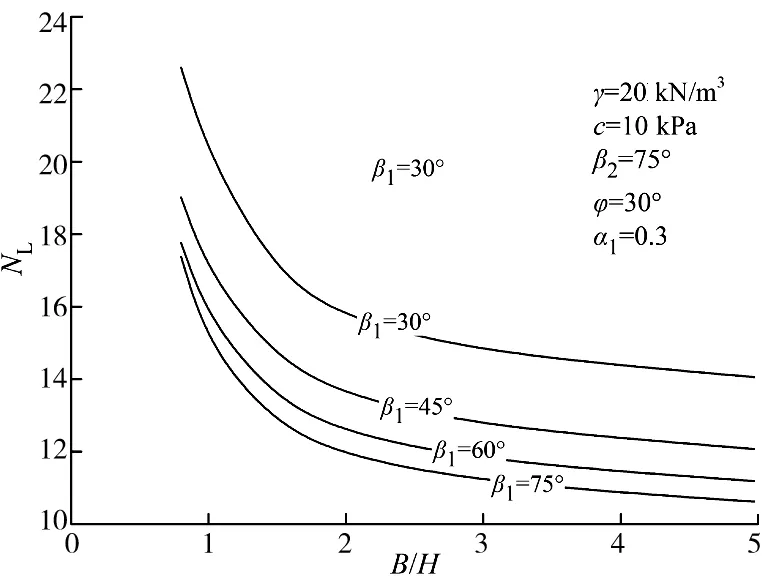
图5　上倾角β1与稳定系数NL的关系Fig.5 Relationships between the slope angle β1 and the stability factor NL

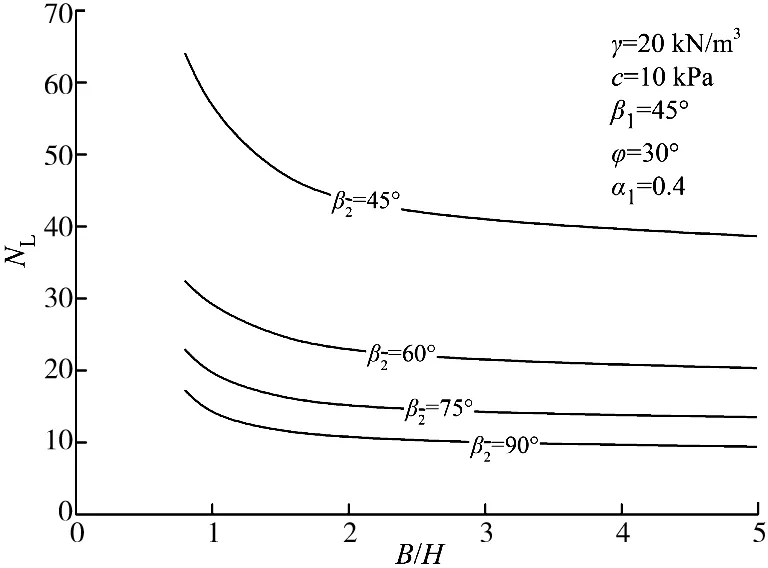
图6　下倾角β2与稳定系数NL的关系Fig.6 Relationships between the slope angle β2 and the stability factor NL

从图3可以看出，当内摩擦角φ增大时，稳定系数NL也将随之增大，即边坡的自稳能力增强，边坡越不容易被破坏。从图4可以看出，当β1<β2时，稳定系数NL随着深度系数的增大而变大。从图5和图6可以看出，对于三维破坏机制，同一宽高比B/H时，稳定系数NL随着倾角β1和β2的增大而减少。同时，依据图3～6可知，当宽高比B/H比较小时，稳定系数的变化很大，边坡的三维效应很明显，随着B/H的增大，稳定系数将逐渐减少，所以边坡的稳定系数也与宽高比B/H的大小有关。

4　结论

1)在β1=β2条件下，二级边坡退化为单级边坡的情形下，与Michalowski研究结果进行了对比。两者结果吻合很好，验证了本文解的有效性。

2)通过计算分析表明，三维边坡宽高比B/H对边坡的稳定性具有重要的影响。当边坡滑移宽度B受到严格限制时，边坡稳定性明显优于二维条件。

3)二级边坡稳定性系数NL随着深度系数α1的增大而变大，而随着深度系数α1的增大，边坡刷坡工程量也在增大，实际工程中应综合考虑这2种因素的影响。

[1] 孙栋梁, 侯克鹏, 杨春丽. 阶梯形边坡简化计算的研究[J]. 矿业研究与开发, 2005, 25(4): 18-19.

SUN Dongliang, HOU Kepeng, YANG Chunli. Research on simplified stability calculation of stepped slope[J]. Mining Research and Development, 2005, 25(4): 18-19.

[2] 时卫民, 叶晓民, 郑颖人. 阶梯形边坡的稳定性分析[J]. 岩石力学与工程学报, 2002, 21(5): 698-701.

SHI Weimin, YE Xiaomin, ZHENG Yingren. Stability analysis of stepped slope[J]. Journal of Rock Mechanics and Engineering, 2002, 21(5): 698-701.

[3] Michalowski R L. Soil reinforcement for seismic design of geotechnical structures[J]. Computers and Geotechnics, 1998, 23(1): 1-17.

[4] 许敬叔, 潘秋景. 盾构隧道开挖面支护力上限分析[J]. 铁道科学与工程学报, 2014, 11(4): 80-84.

XU Jingshu, PAN Qiujing. Upper bound analysis of supporting pressure for shield tunnel faces[J] .Journal of Railway Science and Engineering,2014, 11(4): 80-84.

[5] 杨小礼, 李亮,刘宝琛, 等.偏压隧道结构稳定性的信息优化分析[J]. 岩石力学与工程学报, 2002, 21(4)：484-488.

YANG Xiaoli, LI Liang, LIU Baochen. Evaluation on structure stability of unsymmetrically loaded tunnels using the theory of information optimization analysis [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 484-488.

[6] 王路路, 潘秋景, 杨小礼. 纯黏土坡三维动态上限分析[J]. 铁道科学与工程学报, 2013, 10(2): 87-89.

WANG Lulu，PAN Qiujing，YANG Xiaoli. Three-dimensional upper bound limit analysis for cohesive soil slopes[J].Journal of Railway Science and Engineering,2013,10(2): 87-89.

[7] 杨小礼，眭志荣.浅埋小净距偏压隧道施工工序的数值分析[J].中南大学学报(自然科学版)，2007，38(4)：764-770.

YANG Xiaoli, SUI Zhirong. Numerical simulation of construction sequence for shallow embedded bias tunnels with small clear distance[J]. Jourmal of Center South University(Science and Technology), 2007, 38(4)：764-770.

[8] 王路路, 潘秋景, 杨小礼. 三级台阶边坡稳定性分析的上限解研究[J]. 铁道科学与工程学报, 2013, 10(3): 43-46.

WANG Lulu, PAN Qiujing, YANG Xiaoli. Upper bound solution for stability analysis of tri-beaches slope[J]. Journal of Railway Science and Engineering, 2013, 10(3): 43-46.

[9] YANG Xiaoli, YANG Zihan, LI Yongxin, et al. Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique[J]. Journal of Central South University, 2013, 20(12): 3676-3682.

[10] YANG Xiaoli, ZHANG Daobing, WANG Zuowei. Upper bound solutions for supporting pressures of shallow tunnels with nonlinear failure criterion[J]. Journal of Central South University, 2013, 20(2): 528-535.

[11] Michalowski R L. Three-dimensional analysis of locally loaded slopes[J]. Geotechnique, 1989, 39(1): 27-38.

[12] Farzaneh O, Askari F. Three-dimensional analysis of nonhomogeneous slopes[J]. Journal of Geotechnical and Geo environmental Engineering, 2003, 129(2): 137-145.

[13] Michalowski R L. Slope stability analysis: a kinematical approach[J]. Geotechnique, 1995, 45(2): 283-293.

[14] Michalowski R L, Martel T. Stability charts for 3D failures of steep slopes subjected to seismic excitation[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2011, 137(2):183-189.

[15] Michalowski R L, Drescher A. Three-dimensional stability of slopes and excavations[J]. Geotechnique, 2009, 59(10): 839-850.

3D stability analysis of two-stage slope

TANG Chengtie1, LONG Zexiang2， XU Jingshu2

(1. Hunan Province Lou-Heng Expressway Construction and Development Co, Ltd, Hengyang 421000, China;2. Schod of Civil Engineering, Centre South University, Changsha 410075, China)

This paper constructed a three-dimensional failure mechanism. The analytical solution of the slope height was then deduced on the basis of linear Mohr-Coulomb failure criterion and limit analysis. By virtue of exhaustion method, the numerical results of the stability factor of two-stage slope were derived as well. Moreover, by comparing with the results of Michalowski, the validity of the solution was demonstrated. The results show that: the stability factor of slope not only relates to inclination angle and internal frictional angle, but also relates to depth coefficient and depth-width ratio.

two-stage slope; three-dimensional failure mechanism; linear MC failure criterion; limit analysis; exhaustion method

2016-03-13

国家自然科学基金资助项目(52378510);高速公路横向项目(2015)；2015年中南大学研究生创新项目(2015zzts241)

许敬叔(1988-)，男，山东临沂人，博士研究生，从事交通工程研究；E-mail:461713142@qq.com

TU921

A

1672-7029(2016)10-1940-05