星敏感器APS装配标定系统

李雄风，汪凯巍，白 剑，吕伟振



星敏感器APS装配标定系统

李雄风1，汪凯巍1，白 剑1，吕伟振2

( 1. 浙江大学现代光学仪器国家重点实验室，杭州 310027；2.北京控制工程研究所，北京 100190 )

星敏感器是一种精度达到角秒级的空间姿态测量装置，它的成像组件包括光学镜头和图像传感器(以CMOS APS为主流)。本文主要关注星敏感器APS的装配，从理论上推导了APS的空间位姿参量对计算观测矢量的影响，从而提出了一种在装配过程中控制及标定这些参量的方法并研制了相应的实物系统。测试数据表明，该系统对倾斜的两个分量的标定重复性误差分别为±1.05″和±1.09″，对滚转的标定重复性误差为±9.4″，对偏心的两个分量的标定重复性误差分别为±0.53 μm和±0.55 μm。

星敏感器；APS；标定；自准直仪；图像测量

0 引 言

星敏感器是以星空为运动参照系，以恒星为观测对象的高精度空间姿态测量装置。借助对星空中不同位置的恒星观测，星敏感器能够解算出自身相对于天球的旋转角，从而为各种航空航天飞行器提供准确的空间姿态信息，具有极大的应用价值[1]。与其他姿态测量装置，例如太阳敏感器、陀螺仪、磁力计等相比，星敏感器在高精度和无漂移上尤为杰出，它的姿态测量精度能够达到角秒级乃至亚角秒级[2-4]。

星敏感器相当于一个与微型计算机相连的电子相机[3-4]，它的成像组件包括前置的光学镜头和位于镜头后焦面处的图像传感器。图像传感器的选用目前以CMOS APS为主流。星敏感器的姿态解算过程可以分解为多个步骤，其中的任何一个步骤都有可能在姿态解算的结果中引入误差。本文主要关注星敏感器APS的空间位姿参量，分析它们在姿态解算过程中产生的影响，在此基础上提出了一种在装配过程中控制及标定这些参量的方法，并完成相应的装配标定系统的研制。

1 星敏感器姿态解算

浩瀚星空中分布着众多的恒星，满足一定星等和视场角的恒星都能被星敏感器捕获，从而在APS接收面(像面)上形成圆形亮斑像。尽管不同的星敏感器之间可能存在很多差异，但它们最基本的组成结构是共通的，如图1所示。本文主要涉及的星敏感器组件包括图1中的APS、基准镜、光学镜头。星敏感器以恒星的像为输入信号，经过一系列解算后输出姿态数据。姿态解算过程涉及三个坐标系，它们分别是：

3) 惯性坐标系。其为参考坐标系，即天球坐标系。恒星在惯性坐标系中的观测矢量是已知量。利用至少两颗恒星分别在星敏坐标系与惯性坐标系中的观测矢量，就能计算出星敏坐标系相对于惯性坐标系的旋转角，此即星敏感器的姿态。姿态的表示方法很多，包括姿态矩阵、欧拉角、四元数、旋转矢量等。姿态的计算方法分为静态确定性算法和动态状态估计算法，前者包括TRIAD算法、MLS算法、QUEST算法等，后者一般是卡尔曼滤波方法及其改进[5]。

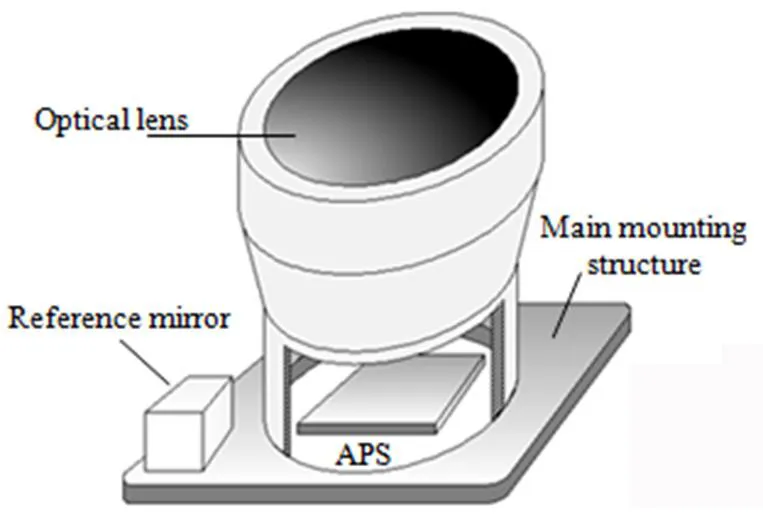
图1 星敏感器通用结构

在星敏感器的装配过程中，控制APS的空间位姿非常重要。如图2所示，在理想状态下，要求和完全重合，此时恒星在中的观测矢量可简单地表示为

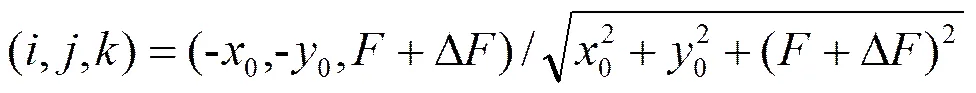
图2 理想状态下的APS

Fig.2 APS under ideal state

然而在实际情况下，如图3所示，由于APS有六个运动自由度，因此在六个自由度上均有可能偏离。其中，和称为倾斜，称为滚转，和称为偏心，称为离焦。在这种情况下计算恒星在中的观测矢量，需将中的质心坐标转换到中，再令其与中的等效针孔坐标相减并归一化，结果得：

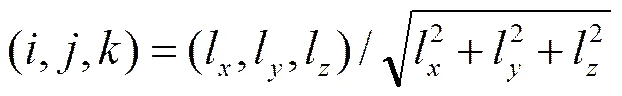
(2)

2 APS装配标定原理

APS的空间位姿主要影响观测矢量的计算精度，进而影响星敏感器最终的姿态解算精度。APS的空间位姿参量包括倾斜、滚转、偏心、离焦。在APS装配中，除了离焦因有特殊要求而不能太小，其它参量应尽量减小，在无法减小的情况下，则应以尽可能高的精度标定这些参量，最后使用式(2)计算观测矢量。

APS空间位姿参量的标定可以在星敏感器装配完成后借助星模拟器并利用成像方法来进行[6-8]。但本文提出的装配标定系统在APS的装配阶段就能对其多个空间位姿参量进行标定，具体内容如下：

(4)

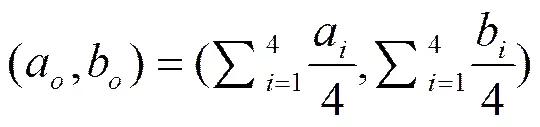
则：

(6)

图像测量系统由定位机构和光电相机组成，它所读取的坐标，来源于构成定位机构的两个正交连接的电控平移台：横坐标即横向平移台的移动量，纵坐标即纵向平移台的移动量。通常在光电相机读取的图像中标记一个像素，并定义平移台定位的坐标总是反映该像素对应的物点位置。通常为了提高图像测量的精度，光电相机读取的是放大像，经视频输出，图像被进一步放大，这往往会给寻找边线或圆周造成极大的不便，也会使取点分布不均而影响最小二乘拟合的结果。为此可从两个方面优化取点过程：

1) 起始点。第一次手动找到该点后，读取并保存其坐标，以后可根据坐标直接找到该点。

2) 后续点。可由起始点推算出来，令平移台自动移动到推算出来的位置，经手动微调后读取坐标。

图4显示了矩形(包括基准镜上表面和APS接收面)边线上的取点过程。出于计算倾角的需要，起始点有两个，规定都在左边线上，且第一个取在远离下端点处，第二个取在下端点附近。设起始点坐标分别为和，则左边线倾角为，atan2表示四象限反正切。后续各点按顺时针方向均匀分布在各边线上。设左边线长为，另一边线长为，则后续各点的坐标依次为

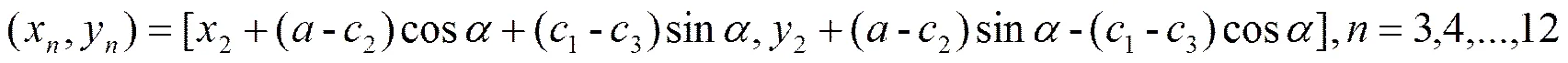
式中：

(8)

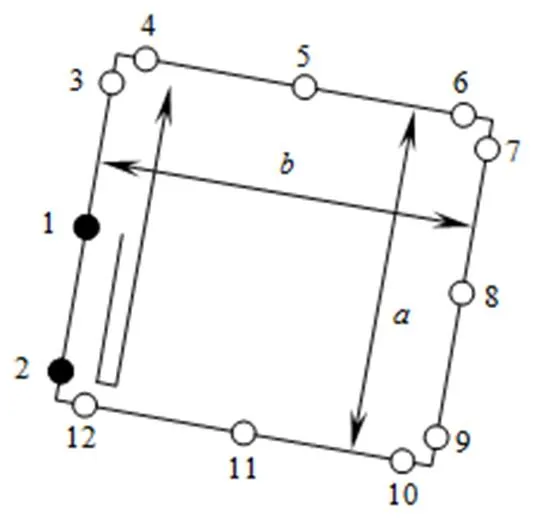
图4 矩形边线坐标读取

图5显示了圆周上的取点过程。规定起始点选取圆周上最左端的点，后续各点按顺时针方向均匀分布在圆周上。设起始点坐标为，圆周半径为，，则后续各点的坐标依次为

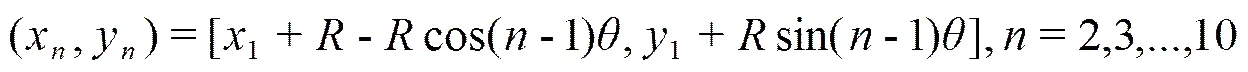
3 装配标定系统研制

图6给出了装配标定系统的组成结构。该系统的核心部件是自准直仪和图像测量系统(其又由定位机构和光电相机组成)。该系统还包含升降机构、角度调节机构，以及作为控制软件载体的计算机。图7给出了装配标定系统的实物模型。在构成图像测量系统时，定位机构在下，光电相机在上。光电相机的光轴应和测量表面垂直，光电相机到测量表面的距离应符合工作距离。在定位机构上连接旋转倾斜台，则能够调整三维角度以满足测量表面和光电相机光轴垂直的要求。将光电相机连接到电控升降台上，则能够调整高度以满足工作距离的要求。自准直仪共有两台，分别可自上而下及自右向左地测量平面法向偏差，分别称为竖向自准直仪(和光电相机共享同一个电控升降台)和侧向自准直仪(单独连接在另一个电控升降台上)。

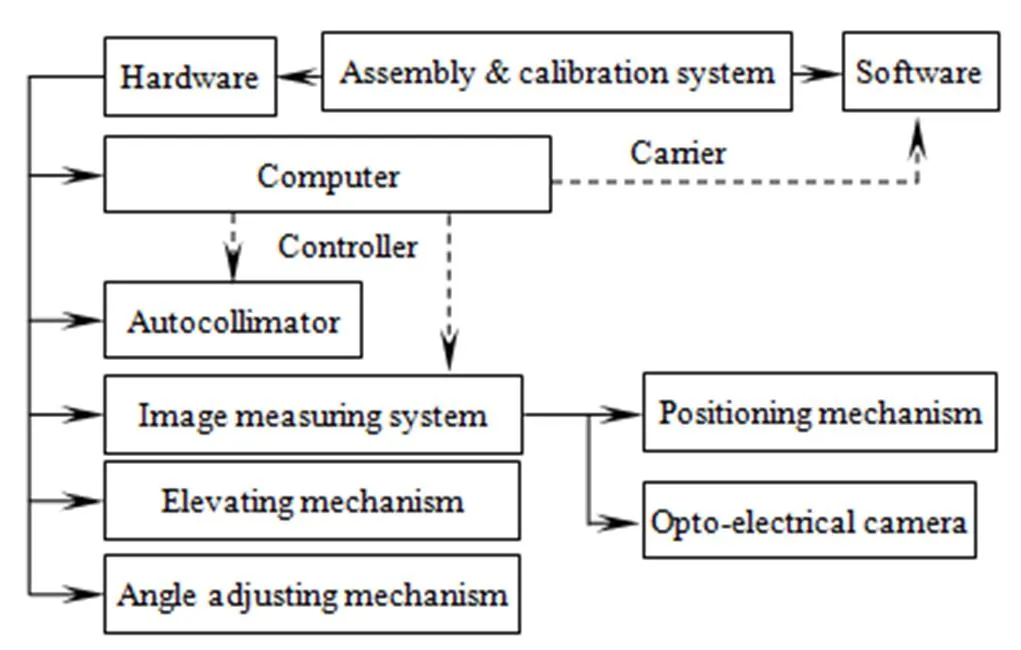
图6 系统组成

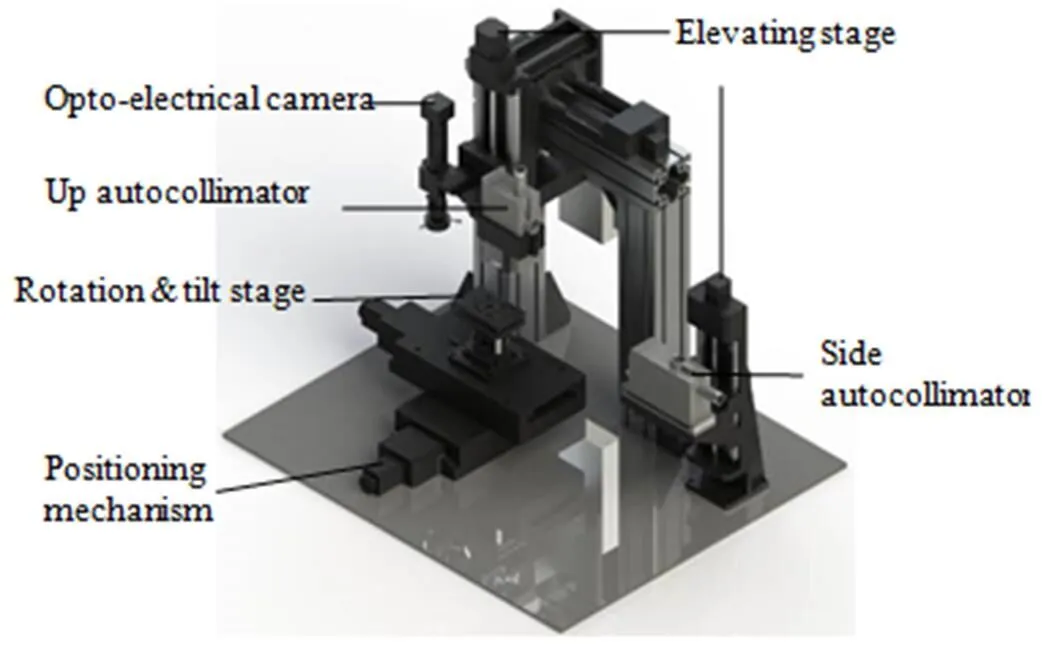
图7 系统模型

将连接了光电相机和竖向自准直仪的电控升降台固定在定位机构正上方的是一个龙门支撑架。支撑架连同上面的器件在重力作用下必然会产生一定形变。竖向自准直仪进行测量时，电控升降台保持静止，该形变可通过调节旋转倾斜台的角度来抵消。图像测量系统进行测量时，电控升降台往往需改变位置。在电控升降台的位置改变前，该形变依然可通过调节旋转倾斜台的角度来抵消。但是，在电控升降台的位置改变后，旋转倾斜台已被锁死，因此产生的形变改变量无法抵消，必须将其控制在较小的范围内。在不断地改良龙门支撑架的结构后，ANSYS的模拟(取电控升降台均匀分布的六个位置)表明形变被控制在微米量级，而形变改变量被控制在亚微米量级，如图8所示。

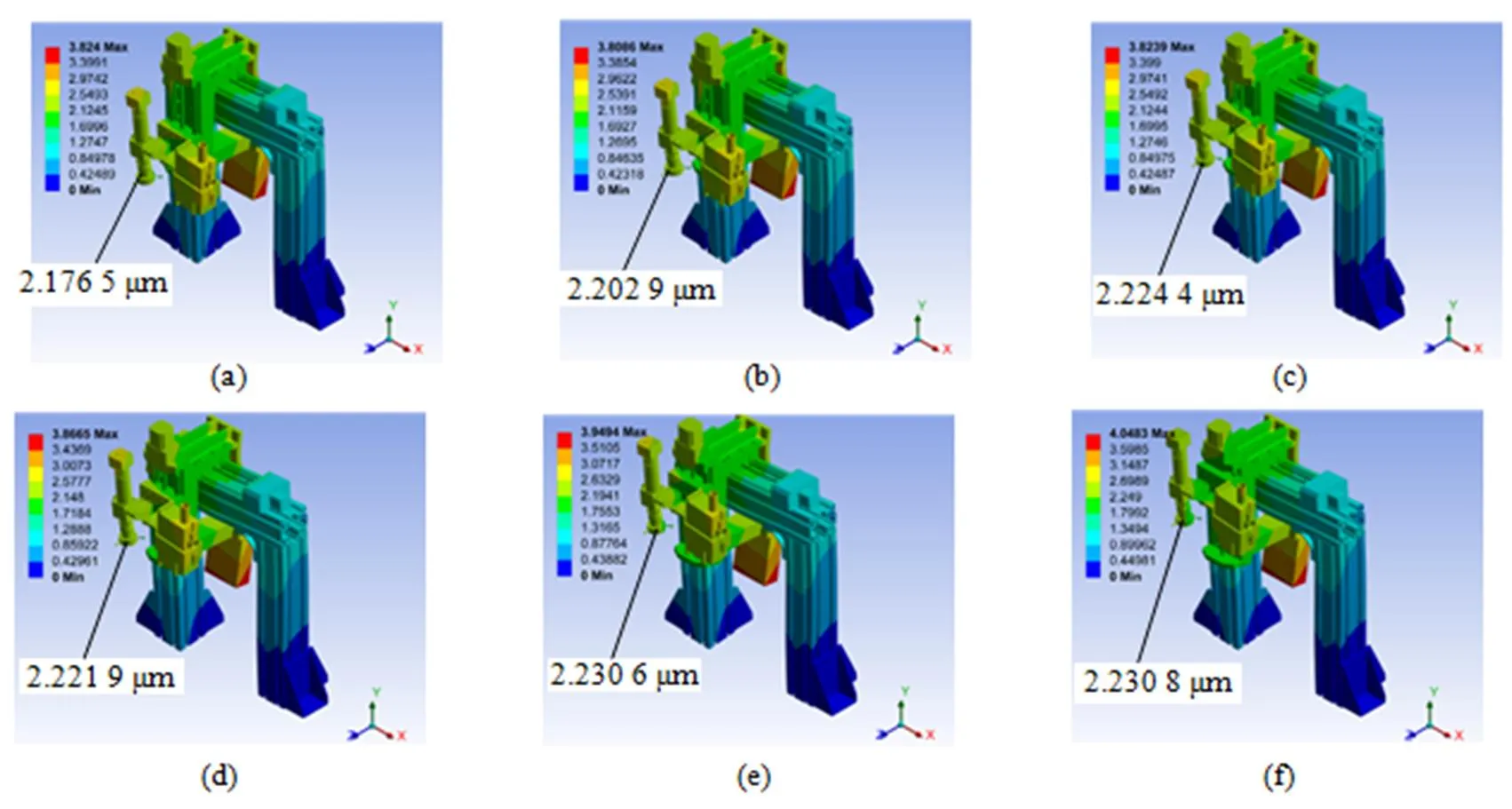
图8 支撑结构静态形变模拟

4 标定误差测试

本文的测试实验使用了上述装配标定系统和北京控制工程研究所研制的微型星敏MST系列。测试实验在气温、湿度、气压均接近恒定的超净室进行。在测试前，保证星敏组件稳固地连接到装配标定系统。

1) 倾斜。测量方法同第2节所述，测量结果如图9所示。在这20组数据中，均值3.6″，标准差1.05″；均值9.7″，标准差1.09″。这表明系统对倾斜的两个分量的标定重复性误差分别为±1.05″和±1.09″。

图9 倾斜测试

2) 滚转。测量方法同第2节所述，测量结果如图10所示。在这20组数据中，均值-4.6″，标准差9.4″。这表明系统对滚转的标定重复性误差为±9.4″。

图10 滚转测试

3) 偏心。测量方法同第2节所述，测量结果如图11所示。在这20组数据中，均值0.135 μm，标准差0.53 μm；均值-3.73 μm，标准差0.55 μm。这表明系统对偏心的两个分量的标定重复性误差分别为±0.53 μm和±0.55 μm。

图11 偏心测试

5 结 论

本文介绍了星敏感器的姿态解算过程，并重点分析了APS的空间位姿参量对计算观测矢量的影响。在此基础上，提出了一种在装配过程中控制及标定APS空间位姿参量的方法，研制了相应的装配标定系统。测试数据表明，该系统对倾斜的两个分量的标定重复性误差分别为±1.05″和±1.09″，对滚转的标定重复性误差为±9.4″，对偏心的两个分量的标定重复性误差分别为±0.53 μm和±0.55 μm。该系统同样适用于其他精密光电成像系统的图像传感器的装配标定。

参考文献：

[1] 刘垒，张路，郑辛，等. 星敏感器技术研究现状及发展趋势[J]. 红外与激光工程，2007，36(增刊)：529-533.

LIU Lei，ZHANG Lu，ZHENG Xin，. Current situation and development trends of star sensor technology [J]. Infrared and Laser Engineering，2007，36(Suppl)：529-533.

[2] Young E F，Mellon R，Percival J W，. Sub-Arcsecond Performance of the ST5000 Star Tracker on a Balloon-Borne Platform [C]// 2012 IEEE Aerospace Conference，Big Sky，MT，Mar 3-10，2012，1：1–7.

[3] Liebe C C，Dennison E W，Hancock B，. Active Pixel Sensor (APS) based Star Tracker [C]// 1998 IEEE Aerospace Conference，Snowmass at Aspen，CO，Mar 21-28，1998，1：119–127.

[4] Liebe C C. Accuracy Performance of Star Trackers – A Tutorial [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251)，2002，38(2)：587-599.

[5] 宋亮亮，张涛，梁斌，等. 基于星敏感器的卫星姿态确定方法研究[J]. 系统仿真学报，2010，22(增刊1)：1-6.

SONG Liangliang，ZHANG Tao，LIANG Bin，. Attitude Determination Method Based on Star Sensor [J]. Journal of System Simulation，2010，22(Suppl.1)：1-6.

[6] WEI Xinguo，ZHANG Guangjun，FAN Qiaoyun，. Star sensor calibration based on integrated modelling with intrinsic and extrinsic parameters [J]. Measurement(S0263-2241)，2014，55：117-125.

[7] XIONG Kun，WEI Xinguo，ZHANG Guangjun，. High-accuracy star sensor calibration based on intrinsic and extrinsic parameter decoupling [J]. Optical Engineering(S0091-3286)，2015，54(3)：034112.

[8] 钟红军，杨孟飞，卢欣. 星敏感器标定方法研究[J]. 光学学报，2010，30(5)：1343-1348.

ZHONG Hongjun，YANG Mengfei，LU Xin. Calibration Method of Star Sensor [J]. Acta Optica Sinica，2010，30(5)：1343-1348.

Assembly and Calibration System for APS of Star Sensor

LI Xiongfeng1，WANG Kaiwei1，BAI Jian1，LÜ Weizhen2

( 1. StateKeyLaboratoryofModernOpticalInstrumentation, ZhejiangUniversity, Hangzhou310027, China;2. BeijingInstituteofControlEngineering, Beijing 100190, China )

Star sensor is a kind of space attitude measurement device whose accuracy reaches arc-second degree, and its imaging module consists of optical lens and image sensor which mainly refers to CMOS APS. The assembly of APS of star sensor is focused, and the influence of spatial position and attitude parameters of APS on the calculation of observation vector is derived theoretically. Thus, a method to control and calibrate these parameters during the process of assembly is proposed, and a corresponding physical system is developed. Test data shows that using this system, the calibration repeatability errors of two components of tilt are ±1.05″ and ±1.09″, respectively, the calibration repeatability error of roll is ±9.4″, and the calibration repeatability errors of two components of eccentricity are ±0.53 μm and ±0.55 μm, respectively.

star sensor; APS; calibration; autocollimator; image measurement

1003-501X(2016)10-0030-06

V448.22

A

10.3969/j.issn.1003-501X.2016.10.006

2015-11-10；

2016-01-15

李雄风(1990-)，男(汉族)，浙江嘉兴人。硕士研究生，主要研究方向是光学精密装调。E-mail: swindlee@foxmail.com。