基于博弈论的航运安全监管对策研究
2016-11-11盛进路杨富华
盛进路,杨富华
(1.重庆交通交通大学 交通运输学院,重庆 400074; 2.国家内河航道整治工程技术研究中心,重庆 400074)
基于博弈论的航运安全监管对策研究
盛进路1,2,杨富华1
(1.重庆交通交通大学 交通运输学院,重庆 400074; 2.国家内河航道整治工程技术研究中心,重庆 400074)
为了解决我国航运安全监管存在的问题,运用博弈理论构建航运安全监管的博弈模型,探讨了安全监管过程中航运企业安全生产和政府部门监管之间的相互博弈机理,研究了博弈双方的静态均衡,给出了混合策略的纳什均衡,并进一步分析了博弈双方的动态演化过程,对航运企业安全生产行为策略选择和政府监管部门监管策略选择的条件和稳定性进行了深入分析。基于复制动态过程分析表明,在一定条件下博弈双方不存在进化稳定策略;局部稳定性分析表明,一定条件下存在局部均衡稳定,有限理性基础上的进化稳定策略与博弈双方的收益、系统所处的初始条件相关,并根据分析结果提出了安全监管对策。
航运;安全监管;演化博弈;复制动态;稳定策略
航运经济活动的安全状态直接关系到航运业的健康发展,更关系到人们的生命财产问题,具有广泛的社会影响。我国先后制订了以《中华人民共和国安全生产法》、《中华人民共和国港口法》、《中华人民共和国内河水上交通安全管理条例》等为主,百余部规章及规范性文件为补充的航运法律体系,航运安全生产法律法规已相对完善,然而险情事故却时有发生。仅2015年我国就发生了两起重大航运安全事故,一起是天津港爆炸事故,另外一起是“东方之星”客船翻沉事故,这给国家和社会带了极大的冲击,对于整个航运界更是影响深远。同时也使得政府监管部门在航运安全监管中所起的作用受到质疑。
目前已有学者围绕航运安全监管问题进行了相关研究,如文献[1]基于模糊综合评价方法构建了航运企业“航运安全”评价模型,对航运安全事故的主要致因进行了分析,划分了航运安全的等级;文献[2]构建了航运安全管理评价体系,从定量的角度分析了航运公司的安全管理体系;为了对航运安全状态进行检测,文献[3]构建了航运安全评价贝叶斯网络模型,对航运安全状态指数进行了精细化描述。也有学者从管理者的角度进行相关研究,如文献[4]通过对特定辖区危险货物运输的作业现状和发展趋势进行分析,提出了建立船载危险货物长效管理机制的构想;文献[5]分析了县域内河的航运安全监管现状,提出了构筑航运安全管理体系的具体建议;文献[6]对内河海事监管模式进行了探索等。然而从整体上看,政府部门和航运企业的行为选择研究较为鲜见。安全事故的发生,不仅仅是安全生产单方面的问题,任何一次安全事故对于监管部门和航运企业来说都隐含了本能的博弈心理,即风险规避和侥幸的利益动机。博弈论是研究博弈双方谋略或决策的理论[7-11],博弈理论在食品安全、煤矿安全、道路运输安全、航空安全等管理领域都取得了较好的应用价值。
基于以上论述,笔者从博弈论的角度,分析航运安全监管过程中利益方的博弈机理,试图通过统一的框架分析观察航运安全监管问题,为我国航运安全监管提供一个理论的视角。
1 模型构建
1.1 基本假设
水上交通安全监管机关主要有海事部门和港航部门等政府监管部门(以下统称监管者);进行水上交通安全生产的主体是航运企业(或称被监管者)。航运企业在进行生产活动时,出于对利益的追求,企业是否按照相关制度进行安全生产和政府部门的监管之间存在着相互的博弈,为此提出以下假设:
假设1 博弈参与方只有被监管者和监管者。
假设2 监管者和被监管者之间不存在合谋的可能;并且监管者是为了取得最大的社会效用,而被监管者则只关心利益最大化。
假设3 监管者在博弈中采取“监管”策略的概率为θ(0≤θ≤1),“不监管”的概率则为1-θ,监管者的监管成本为C1。
假设4 被监管者采取“安全生产”的概率为λ(0≤λ≤1),被监管者不按规定进行安全生产的概率为1-λ,被监管者进行安全生产的成本投入为C2。
假设5L为监管者能从被监管者安全生产中获得的收益;W为被监管者能从安全生产中获得的收益;H为被监管者进行安全生产时获得的便利或奖励(如企业诚信等级提高、特别服务等);T为被监管者不安全生产而受到的监管处罚(如罚款、企业信誉降低等,对监管者而言是等额的罚款收益、政府声誉收益);G为监管者不监管受到的损失;K为被监管者进行不安全生产时获得的超额利益。
1.2 博弈模型
在监管者和被监管者之间进行的无限次博弈中,被监管者有两种行为选择:一是按照有关法律、法规正规运行,即安全生产;二是其不完全遵守法律法规进行运行,即不安全生产,可将策略集简化为A1={安全生产,不安全生产}。监管者的行为选择为:一是对相关单位进行安全生产监管;二是不对相关单位进行安全生产监管,策略集可简化为A2={监管,不监管},监管者与被监管者的博弈树模型如图1所示。
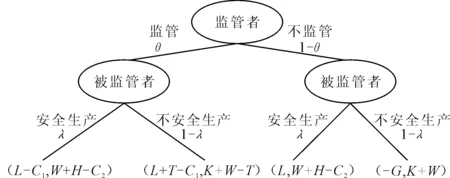
图1 监管者与被监管者的博弈树模型
显然,对于被监管者而言,未进行安全生产的超额利润较其进行安全生产得到的收益较高的,即K>0,否则被监管者没有必要冒险。同时假设监管者只要监管定能查处被监管者的不安全生产行为,根据以上假设和模型可构建两者的安全监管博弈矩阵,如表1所示。

表1 监管者和被监管者安全监管的博弈矩阵
2 静态均衡分析
基于上述博弈机理,监管者和被监管者是存在混合策略纳什均衡,则在给定被监管者安全生产概率λ的情况下,监管者监管和不监管的期望收益分别为
(1)
(2) 当监管和不监管的期望收益相等时,可以得到被监管者安全生产的最优概率,令I1=I2,则
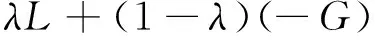
(3)
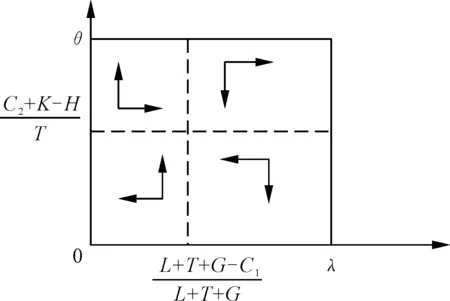
(4) 假定C1 在给定θ条件下,被监管者进行安全生产和不安全生产的期望收益分别为 (6) 当安全生产和不安全生产的期望收益相等时,可得到监管者监管的最优概率,令I3=I4,则 (7) (8) 式(8)表明,监管者监管行为选择,取决于被监管者从安全生产生产中获得的便利、被监管者进行安全生产的投入、不安全生产时获得的超额利益和进行不安全生产时受到的处罚。 综上可得,混合策略的纳什均衡为 (9) 3.1 进化复制动态分析 在复杂的社会环境下,被监管者和监管者之间决策者的完全理性显然具有一定局限性,这决定了双方在一开始往往不可能找到最优策略,随着一定规模群体中成员的反复博弈、不断摸索,其特征会表现出生物的进化特征,博弈过程呈现的是一种动态的均衡。对于被监管者而言 被监管者复制动态方程为 图2 航运企业群体博弈复制动态相位图 (12) 监管者的复制动态方程为 图3 政府部门博弈群体复制动态相位图 由此可见,监管者监管的成本大于监管的总收益时,监管者会选择不监管策略,而当监管者监管的成本小于监管的总收益时,监管者的策略选择取决于被监管者安全生产的概率,被监管者采用安全生产的概率越大,则监管者越可能采取不监管策略。 3.2 演化稳性分析 若将被监管者和监管者的种群复制动态关系用一个坐标平面表示,即可以得到复制动态关系和稳定性图,如4图所示。从图4可以看出,没有策略点满足复制动态的收敛性和干扰性。当监管者采取大于(C2+K-H)/T的概率进行监管,被监管者会采取安全生产策略,而当被监管者进行安全生产时,出于对监管成本的考虑,监管者会不监管。一旦监管者不监管,被监管者则不进行安全生产投入,博弈策略处于无限的循环往复当中,无法消除被监管者的不安全生产行为。 图4 复制动态关系和稳定性图 (14) 矩阵J的行列式为: (15) 矩阵J的迹为: (16) 根据雅可比矩阵局部稳定性分析,可得5个均衡点的局部稳定性情况,如表2所示。 表2 局部稳定性分析表 由表2可知,在博弈过程中,随着条件的变化,系统有3个局部的稳定均衡点,即(0,0)、(0,1)、(1,0)。可见其演化稳定性策略分别为:(不监管,不安全生产)、(不监管,安全生产)、(监管、不安全生产)。①(0,0)点对应的是被监管者采取不安全生产策略,监管者采取不监管策略。即被监管者获得的差额利润较大,同时监管者成本较高,成本大于了监管的收益和不监管导致的损失之和,宁可选择放弃监管,而被监管者则处于中间状态,既有选择安全生产的也有选择不安全生产的,但最终会向不安全生产演化。②(0,1)对应的是被监管者采取安全生产策略,监管者采取不监管策略。即当被监管者在从安全生产中获得的便利大于不安全生产的超额利润和付出的安全生产成本时,被监管者会毅然选择安全生产策略;而监管者则为中间状态,既有监管又有不监管策略,最终会向不监管演化。③(1,0)对应的被监管者选择不安全生产,监管者监管。被监管者不安全生产时获得的超额利润除去受到的处罚外还大于进行安全生产时获得的总收益,其宁可选择不安全生产,监管者则会因为监管成本较低,从监管中的获利更多而选择监管。 通过博弈理论构建了航运安全监管的博弈模型,分析了静态博弈下的均衡以及不同情形下的模型的进化稳定策略,得出如下结论和建议: (1)航运企业是否采取安全生产策略与安全生产成本、安全生产得到的便利、不安全生产时的超额利润以及不安全生产时受到的处罚直接相关。因此,政府在进行监管时,一方面应加强对不安全生产行为的处罚,使企业不安全生产成本增加,迫使航运企业采取安全自查,消除安全隐患,从而提高安全生产的概率;另一方面,采取降低超额利润的分配比例手段,使航运企业不安全生产的超额利润降低,同时积极引导安全生产行为,给予安全生产企业相应的便利,从而使市场形成安全生产导向。 (2)监管部门是否采取监管策略与监管部门从企业安全生产中获得的收益、从企业不安全生产中获取的处罚、不监管时受到的损失及监管的成本相关。监管成本过高时,会使监管部门放弃监管,因此一方面可以采用加大企业不安全生产的惩罚进行填补;另一方面,注重长效机制的建立,实施差异化监管,提高监管效率和资源利用率。此外应加强监管责任的落实,加大对渎职行为的惩处。 (3)注重构建第三方监督,使博弈双方的策略受到新条件的制约。加强对监管部门“不作为”的网络监督力度,通过舆论压力增强监管部门的积极作为;拓展企业不安全生产的曝光渠道,扩充企业不安全生产监督链条。 [1] 李振福,薛非.航运企业航运安全评价研究[J].中国安全科学学报,2009,19(4):102-107. [2] 胡甚平,许玲,席永涛,等.基于云模型的航运公司安全管理分级评价方法[J].中国安全科学学报,2013,23(10):140-144. [3] 李昊,张庆年.内河航运安全状态监测与指数体系研究[J].中国安全科学学报,2014,24(10):95-100. [4] 林永革.浅议建立船舶载运危险货物长效管理机制[J].中国海事,2008(5):47-49. [5] 刘国利.构筑内河航运安全管理体系[J].中国水运,2005(5):22-23. [6] 黄锦标.内河海事监管模式探索[J].世界海运,2010(12):28-31. [7] 李建民,郑中义,齐迹.海上危化品运输系统安全管理博弈模型[J].中国航海,2014(1):56-60. [8] 张良桥,马丛文.理性与有限理性:论经典博弈理论与进化博弈理论之关系[J].世界经济,2001(8):74-78. [9] THEODOROS S,KONSTANTINOS M,ALEXIOS M .A game theoretical method for cost-benefit analysis of malware dissemination prevention[J].Information Security Journal,2015,24(4):164-176. [10] ZHANG S K,ZHANG Y D. Introduction to game theory[J].Chinese Science Bulletin,2003,48(9):841-846. [11] 孙庆文,陆柳,严广乐,等.不完全信息条件下演化博弈均衡的稳定性分析[J].系统工程理论与实践,2003,23(7):12-15. [12] FRIEDMAN D. Evolutionary games in economics [J] Econometrica,1991,59(3):637-666. SHENG Jinlu:Associate Professor; college of Traffic and Transportation, Chongqing Jiaotong University, Chongqing 400074, China. Shipping Safety Regulation Strategy Based on Game Theory SHENGJinlu,YANGFuhua Game theory is applied to study shipping safety regulation of our country to solve regulation problem,setting up shipping safety supervision game model,relationship between players is probed,giving Nash equilibrium strategy. Behavior both sides is analyzed. The article analyzes the conditions and stability of the choice of the safe production behavior strategy and the supervision strategy choice of the government supervision department. Based on replicated dynamic process analysis ,under certain conditions, there is no evolutionary stabilization strategy. Local stability analysis shows that there exists no evolutionary stable strategy in certain condition. Evolutionary stable strategy is based on bounded rationality,game benefit,and system of initial conditions. According to the results,safety regulation suggestion is proposed. shipping;safety regulation;evolutionary game;replicator dynamics;stable strategy 2095-3852(2016)05-0548-05 A 2016-05-24. 盛进路(1976-),男,山东烟台人,重庆交通交通大学交通运输学院副教授. 长江航务管理局科技研发资金项目(201562);国家内河航道整治工程技术研究中心暨水利水运教育部重点实验室开放基金项目(SLK2015B10). U698 DOI:10.3963/j.issn.2095-3852.2016.05.007
3 博弈演化分析


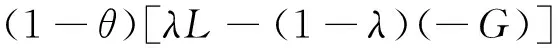


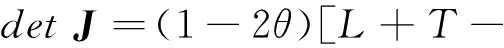


4 结论与建议
