基于风光互补的配电系统随机潮流研究
2016-11-11邵沈会李宝国鲁宝春
邵沈会,李宝国,鲁宝春
(辽宁工业大学 电气工程学院,辽宁 锦州 121001)
基于风光互补的配电系统随机潮流研究
邵沈会,李宝国,鲁宝春
(辽宁工业大学 电气工程学院,辽宁 锦州 121001)
针对风光电源接入电网造成不稳运行状况,建立了分布式电源配电系统的随机潮流计算模型,提出了一种基于半不变量法与Gram-Charlier级数展开相结合的改进混合随机潮流算法,并用“峰压比”指标来定量分析风电与光伏按不同比例接入时对配电系统的影响程度。通过IEEE-33节点配电系统算例仿真分析,验证了该算法的有效性以及“峰压比”指标的可行性。
风光互补;配电系统;随机潮流;半不变量;概率分布
随着新能源技术的快速崛起,大量强随机性弱可控性的分布式电源被不断地接入到电网中来,清洁高效的新能源电动汽车以及各种主动式负荷也将接入到配电网,致使配电系统出现分布式电源出力间歇式波动、负荷功率随机变化等不确定因素。传统的确定性潮流分析方法计及系统的各种不确定因素,需要对各种情况做大量运算,不仅计算量大,而且很难反映系统的整体状况。目前,随之衍生而来的随机潮流计算则能较好地解决这一难题。随机潮流[1-2](Probabilistic Load Flow,PLF)计算就是用相关的概率理论来描述系统的不确定性,建立系统的随机模型,研究相应的概率算法并且应用于工程实际,也称之为概率潮流计算。它能够充分考虑系统的负荷波动、发电机故障停运、线路随机故障、间歇性能源出力波动等电力系统运行中的各种随机因素,并得到系统稳态运行情况下的宏观统计信息[3],而且对电网存在的薄弱环节能做出量化分析。随机潮流广泛应用于短期以及中长期电网规划等,可以为规划和调度部门提供极具参考价值的信息,具有一定的理论意义和实用价值。因此本文对风电与光伏按不同比例接入配电网时的随机潮流进行了计算。
1 系统随机模型
1.1风电场出力随机模型
1.1.1风速随机模型
国内外提出了很多的模型来模拟风速的随机分布,如瑞利分布、Γ分布、耿贝尔分布、威布尔分布等。其中威布尔分布被公认为是描述风速分布最好的模型,因此本文采用风速的双参数威布尔分布模型,其概率密度函数为
式中:v表示风速;k称作威布尔分布的形状参数,反映风速分布的特点;c称作威布尔分布的尺度参数,反映该地区平均风速的大小。风速的分布图如图1所示。

图1 风速的双参数威布尔分布曲线图

1.1.2风力发电机输出功率随机模型
知道了风速的随机分布,就可以通过风力机组的输出功率与风速之间的关系得到输出功率的随机分布。风力机组有功出力与风速之间的关系如图2所示。

图2 风力发电有功出力与风速的关系
根据图2可以得到风力发电机有功出力与风速之间的函数表达式为
式中:Pr为风力发电机额定功率;vci为切入风速;vr为额定风速;vco为切出风速。
风力发电机有功出力的概率分布可由风速的概率分布和发电机的功率特性求出:
1) 当v≤vci∪v≥vco时,PW=0

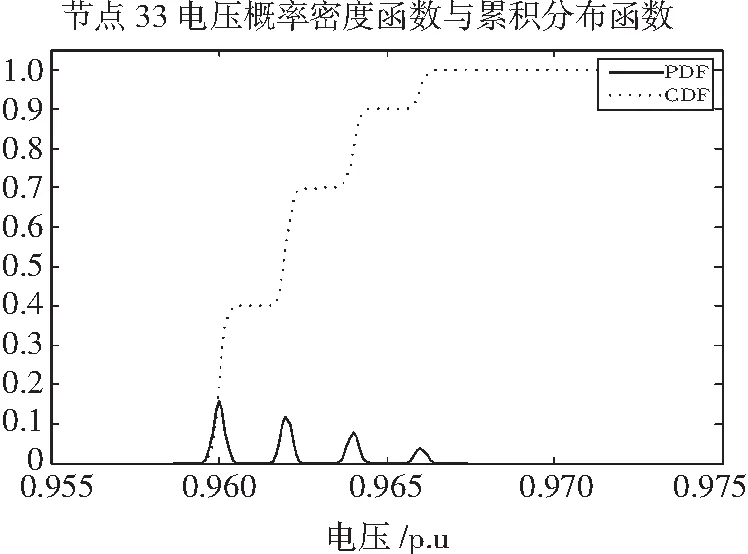
2) 当vci 3) 当vr≤v 由此可知,其有功出力的概率分布在风电机组零出力和额定出力点处是非连续的,因此,为了使随机潮流计算精度更加准确,将风电机在零出力和额定出力之间的概率分布离散化,如图3所示。 图3 风电机有功出力概率分布离散化示意图 对于离散点PW有 P(PW)=P(PW1 并网运行的风力发电系统大多采用异步发电机,并不产生无功,而为建立旋转磁场,需要向电网吸收无功功率,且通过并联补偿器保持功率因数不变,因此,可将风力发电机简化为PQ节点,即无功功率Q为 Q=Ptanφ 由有功出力与无功功率的关系可知,风电机组出力的概率分布可以用有功功率与无功功率及相应概率的离散数据来表示。 1.2光伏出力随机模型 1.2.1太阳能光照强度分布的随机模型 根据大量的历史统计数据显示,在若干小时的时间段内太阳光照强度近似服从Beta分布[5],其概率密度函数为 (1) 式中:r为某时刻的实际光照强度,W/m;rmax为这段时间内的最大光照强度,W/m;α和β均为Beta分布的形状参数;Γ为Gamma函数。 1.2.2光伏发电系统输出功率的随机模型 知道了光强的随机分布模型之后,便可由光伏发电系统的输出功率与光强的近似关系求出输出功率的随机分布,即 PM=A·r·η (2) 通过式(1)和式(2)可以得到太阳能电池方阵输出功率的概率密度函数: 光伏发电系统并网时,通常由并网逆变器自动投切来使其输出功率为单位功率因数,因此在潮流计算中可以将光伏发电系统看作无功出力为零的PQ节点。 本文采用的计算模型基于线性化潮流方程,考虑的随机因素包括风电出力、光伏发电出力的不确定性,常规发电机组故障停运出力的不确定性以及负荷功率波动的不确定性等,并将各节点视为相互独立的随机变量。系统的潮流方程可表示为 (3) 式中:W为节点注入量,包括各节点有功、无功;X为节点状态变量,包括各节点电压幅值和相角;Z为各支路潮流。 考虑到节点注入功率的随机性,将式(3)在基准运行点处线性化可得 (4) T0=G0S0 式中:J0为确定性潮流计算最后一次迭代的雅可比矩阵;S0称为灵敏度矩阵,通过对雅可比矩阵J0求逆得到;X0为基准运行点处状态变量的期望值,通过卷积运算可求式(4)的状态变量。 为减少计算量,本文采用半不变量法和Gram-Charlier展开级数相结合来取代卷积计算。 半不变量具有重要的可加性,能够避免复杂的卷积运算。随机变量的各阶半不变量与其原点距的关系为 k1=m1 式中:kr、mr分别为随机变量的半不变量和原点矩;r为阶数。由此,已知原点矩即可求其各阶半不变量,反之亦然。 Gram-Charlier级数展开式把随机变量的分布函数表达为由正态随机变量各阶导数组成的级数,而级数系数则由该随机变量的各阶半不变量组成。 根据Gram-Charlier级数展开理论,随机变量的概率密度函数f(x)和累积分布函数F(x)可分别表示为 用gv表示v阶规格化后的半不变量,即 Hγ+1(x)=xHγ(x)-γHγ-1(x),γ≥1 4含分布式电源的配电系统随机潮流计算流程 本方法只考虑各节点注入功率相互独立的情况,暂不考虑线路随机停运等问题。用半不变量结合Gram-Charlier级数展开求随机变量的概率分布,只有当随机变量的偏度系数γ1和峰度系数γ2都接近于0时,所求的概率分布才有效,否则其概率密度曲线会出现负值或大于1的值,从而使得概率密度曲线失真。当配电网中接入的分布式电源概率输出的波动性较大时,便会导致Gram-Charlier级数展开式的偏度系数γ1和峰度系数γ2远偏于0,使得此方法不能准确描述随机变量的概率分布。针对这一弊端,提出一种基于半不变量的改进随机潮流算法,计算流程如图4所示。 图4 改进的含分布式电源的配电网随机潮流计算流程 以IEEE-33节点配电网络[6]系统为例,在系统基础上加入分布式电源,通过MATLAB7.1来编制分布式电源接入配电系统后的随机潮流程序。仿真分析分布式电源接入种类与接入容量的不同对配电网潮流的影响,以便为配电网规划人员提供更全面有用的信息。IEEE-33节点配电网络接线如图5所示。 图5 IEEE 33节点配电系统接线图 5.1不同类型分布式电源接入对配电系统的影响 可分如下4种情况来讨论。 Case1:系统没有任何分布式电源接入,只有负荷的随机变化。 Case2:系统末端第33节点处接入一个额定功率为100 kW的风力发电机。 Case3:系统末端第33节点处接入一个额定功率为100 kW的光伏发电系统。 Case4:为了使得所接入的分布式电源总功率不变,在末端第33节点接入一个额定功率为50 kW的风力机和一个额定功率为50 kW的光伏发电系统。 对于Case1,首先用牛顿-拉夫逊法进行确定性潮流计算得到正常状态下的节点状态变量和支路潮流情况,并且可以作为随机潮流计算的期望值。 然后结合所编制的半不变量法和Gram-Charlier级数展开随机潮流程序便可求出各节点电压以及支路潮流的概率密度函数和累积分布函数。以系统末端节点33为例,取离散点步长为0.0001,通过MATLAB仿真得到其节点电压的概率密度函数曲线(PDF)和累积分布函数曲线(CDF)如图6所示。 图6 Case1情况下节点33电压的概率密度函数 对于Case2中风力发电系统,由已知数据可求出风速随机模型中风速的形状参数k=2.80,尺度参数c=5.14。风力发电机输出功率的随机参数k1=0.0091,k2=-0.0273。从而可求出风力发电随机出力的各阶矩,然后由矩与半不变量的关系即可得到其各阶半不变量。 对于Case3中光伏发电系统,由原始数据可得光强Beta分布的形状参数α=0.45,β=9.19,再通过矩与半不变量的关系可得光伏电池随机出力的各阶矩与各阶半不变量。 对于Case4中的风光混合发电系统,由于额定功率都缩小一半,相应的参数也要减小,同理,通过编程计算得到风光混合发电系统有功出力的各阶半不变量。 在求出风力发电机和光伏发电系统输出功率的各阶半不变量后,根据本文编制的基于半不变量法的Gram-Charlier级数展开随机潮流计算程序,可以分别求出Case2、Case3和Case4中各节点状态变量的各阶半不变量以及概率分布函数。这三种情况下节点33电压的概率密度函数和累积分布函数如图7~9所示。 图7 Case2情况下节点33电压的概率密度函数和累积分布函数 图8 Case3情况下节点33电压的概率密度函数和累积分布函数 图9 Case4情况下节点33电压的概率密度函数和累积分布函数 通过比较Case2和Case3可知,在额定容量相同的情况下,光伏发电随机出力使得节点电压的波动性比风力发电更大,同时光伏发电对系统末端节点电压的改善程度也比风力发电要大。通过比较分析Case2、Case3和Case4的概率分布图形可知,在额定功率相同的情况下,风光互补混合发电系统接入配电网时造成的节点波动情况较单一类型分布式电源接入时要小。 四种情况下节点33的前4阶半不变量以及偏度系数和峰度系数计算如表1所示。 表1 几种情况下节点33前4阶半不变量和偏度、峰度系数Table 1 Node 33 first 4 order semi invariant and skewness,kurtosis coefficient in several cases 由表1分析可知,节点电压的偏度系数γ1和峰度系数γ2的值越大,其概率密度曲线的波动性就越大,使得其畸变率越大。对于Case2、Case3和Case4三种情况可以看作风力发电与光伏发电容量的比例不同对33节点电压产生的不同影响。其不同容量比例时的节点电压波动情况如表2所示。 综上所述,当没有风电与光伏接入配电系统时,节点电压的随机波动符合正态分布。而当有风电与光伏接入时,虽然线路电压有所改善,但风电与光伏出力的随机性使得节点电压波动增大,概率密度曲线会出现小于零而累积分布函数曲线出现大于1的值。 表2 风力发电与光伏发电不同容量比时 节点33电压波动情况Table 2 Node 33 voltage fluctuation of wind power generation and photovoltaic power generation under different capacity 5.2“峰压比”指标的提出 由概率理论可知,峰度系数要比偏度系数能更加直观准确地反映曲线的畸变情况。本文考虑用不同种类分布式电源接入到配电系统所带来的节点电压变化量与对应的峰度系数的比值作为标准来衡量其对系统的影响程度,把它定义为峰压比,即 (5) 由于节点电压的波动幅度要比对应峰度系数小,因此ξ值越大,说明对系统的影响越小。根据表1再结合式(5)可以分别得到其峰压比如表3所示。 表3 三种不同情况下的ξ值Table 3 ξ value of three different cases % 从表3可知,在系统额定容量相同的情况下,Case4对应的峰压比要大于Case2对应的峰压比,同时Case2对应的峰压比又大于Case3对应的峰压比。所以说风光互补发电系统接入对配电系统最有利,其次是单独风电接入系统,而光伏发电对系统的影响要大一些。 5.3风电出力较大时改进的随机潮流算法应用 当系统风电出力过大时,其强随机性和波动性使得Gram-Charlier级数展开式中的偏度系数γ1和峰度系数γ2的绝对值远大于零,之前的随机潮流算法求得的概率分布将会严重失真。为此,采用改进随机潮流算法可以有效地处理分布式电源波动较大的情况。 由于风力发电机有功出力的概率分布在风电机组零出力和额定出力点处是非连续的,为了使随机潮流计算精度更加准确,将风电机在零出力和额定出力之间的概率分布离散化,离散化的结果如表4所示。 表4风电出力离散化结果 Table 4Wind power output discretization result 由此,可以根据离散结果求出其有功出力的各阶半不变量以及对应的状态变量的各阶半不变量,再由半不变量与矩的关系得到各阶矩,然后由Von Mises法拟合其概率分布,最后与状态变量对应的正态部分进行卷积得到最终的概率分布。应用此改进算法求得节点33的电压概率密度函数和累积分布函数如图10所示。 图10 改进的节点33电压概率密度函数与累积分布函数 对比图7和图10可知,应用改进的潮流算法节点33的电压波动得到了明显的改善,波动范围有所减少,而且其概率密度函数和累积分布函数曲线没有发生畸变。因此改进的含分布式电源的配电网随机潮流算法能够有效处理分布式电源波动性较大的情况。 本文通过半不变量和Gram-Charlier展开级数相结合的方法计算出配电网各节点电压和支路潮流的概率分布,并且针对风电出力波动较大时Gram-Charlier展开级数的概率分布失真的弊端,提出了一种改进的混合随机潮流算法。通过算例仿真的计算与分析证明了改进的混合随机潮流算法的有效性和“峰压比”指标的准确性。 [1] ACKERMANN T, ANDERSSON G, SODER L. Distributed generation: a definition[J]. Electric Power System Research, 2001, 57(3): 195-204. [2] BORKOWSKA B. Probabilistic load flow[J]. IEEE Transactions on Power Apparatus and Systems, 1974, 93(3): 752-759. [3] USAOLA J. Probabilistic load flow with correlated wind power injections[J]. Electric Power Systems Research, 2010, 80(5): 528-536. [4] 徐卫民, 张星琳, 孔新红. 三种计算风速威布尔分布参数的比较[J]. 江西电力, 2007, 31(1): 1-3. XU Weimin, ZHANG Xinglin, KONG Xinhong. Comparison for three methods to calculate weibull distribution parameters of wind speed[J]. Jiangxi Electric Power, 2007, 31(1): 1-3. [5] ABOUZAHR I, RAMAKUMAR R. An approach to assess the performance of utility-interactive photovoltaic systems[J]. IEEE Transactions on Energy Conversion, 1993, 8(2): 145-153. [6] KERSTING H W. Radial distribution test feeders[J]. IEEE Transactions on Power Systems, 1991, 6(3): 975-985. (责任编辑郭金光) Research on probabilistic load flow of distribution system based on wind and solar hybrid generation SHAO Shenhui, LI Baoguo, LU Baochun (Electric Engineering College, Liaoning University of Technology, Jinzhou 121001, China) Aiming at the unstable operation of power grid after the integration of wind and solar power source, this paper established the probabilistic load flow calculation model of distribution system with distributed power supply, proposed the improved hybrid probabilistic load flow algorithm based on the combination of semi-invariant and Gram-Charlier series expansion, and adopted ‘kurtosis-voltage-ratio’ index to make quantitative analysis of the influence of the integration with different proportion of wind and photovoltaic power on distribution system. Through the simulation of IEEE-33 node distribution system, it verifies the effectiveness of the method and the feasibility of ‘kurtosis-voltage-ratio’ index. wind and solar hybrid generation; distribution system; probabilistic load flow; semi-invariant; probability distribution 2016-03-26。 邵沈会(1990—),男,硕士研究生,研究方向为电力系统稳定性分析与控制。 TM744+.2 A 2095-6843(2016)04-0357-06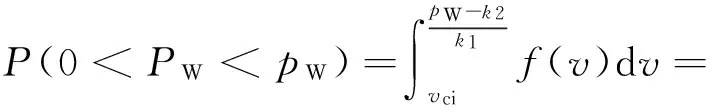




2 随机潮流计算模型

3 相关概率理论和算法研究


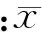


5 算例仿真分析









6 结 论
