List improper coloring of graphs of nonnegative characteristic

XU Yang

（College of Science and Information，Qingdao Agricultural University，Qingdao Shandong　266109，China）

List improper coloring of graphs of nonnegative characteristic

XU Yang

（College of Science and Information，Qingdao Agricultural University，Qingdao Shandong266109，China）

A graph G is called（k，d）∗-choosable if，for every list assignment L with|L（v）|= k for all v∈V（G），there is an L-coloring of G such that every vertex has at most d neighbors receiving the same color as itself.Let G be a graph embedded in a surface of nonnegative characteristic.In this paper，we prove that if G is a 2-connected graph，which contains no 5-cycles，adjacent 3-faces and adjacent 4-faces，then G is（3，1）∗-choosable.

list improper coloring；characteristic；cycle；Euler's formula

Article ID：1000-5641（2016）02-0051-05

0　Introduction

All graphs considered in this paper are finite，simple and undirected.For a graph G，we denote its vertex set，edge set，face set，and minimum degree by V（G），E（G），F（G）and δ（G），respectively.

A graph G is k-colorable with impropriety d，or（k,d）∗-colorable，if G has a vertex coloring φ using k colors such that each vertex has at most d neighbors receiving the same color as itself. A（k,0）∗-coloring is an ordinary proper k-coloring.A list assignment of G is a function L that assigns a list L（v）of colors to each vertex v∈V（G）.An L-coloring with impropriety d，or（L,d）-coloring，is a mapping φ that assigns a color φ（v）∈L（v）to each vertex v∈V（G）such that v has at most d neighbors receiving the same color as itself.A graph is k-choosable with impropriety d，or（k,d）∗-choosable，if there exists an（L,d）-coloring for every list assignment L with|L（v）|=k for all v∈V（G）.Note that（k,0）∗-choosability is just the ordinary kchoosability.

The notion of list improper coloring was introduced byˇSkrekovski［1］and，independently by Eaton and Hull［2］.They proved that every planar graph is（3,2）∗-choosable and every outerplanar graph is（2,2）∗-choosable.ˇSkrekovski proved in［3］that every planar graph without 3-cycles is（3,1）∗-choosable，and in［4］that every planar graph G is（2,1）∗-choosable if its girth g（G）≥9，（2,2）∗-choosable if g（G）≥7，（2,3）∗-choosable if g（G）≥6，and（2,d）∗-choosable if g（G）≥ 5 and d≥4.Lih et al.［5］proved that every planar graph without 4-cycles and k-cycles for some k∈｛5,6,7｝is（3,1）∗-choosable.Xu and Yu［6］proved that every toroidal graph containing no adjacent triangles and no 6-cycles and l-cycles for some l∈｛5,7｝is（3,1）∗-choosable.Zhang［7］proved that every toroidal graph containing no 5-cycles and 6-cycles is（3,1）∗-choosable.Chen et al.［8］proved that every graph embedded in a surface of nonnegative characteristic，which contains no k-cycles with a chord for all k=4,5,6，then G is（3,1）∗-choosable.

This paper investigates improper choosability for graphs of nonnegative characteristic. The characteristic of a surface is equal to|V（G）|-|E（G）|+|F（G）|for any graph G that is 2-cell embedding.In this paper，we use the method different from Chen et al.［8］which use discharge rules，and prove that if G is a 2-connected graph，which contains no 5-cycles，adjacent 3-faces，and adjacent 4-faces，then G is（3,1）∗-choosable.This can be regard as a complement to the result of［8］.

1　Preliminaries

Let G be a graph embedded in a surface of nonnegative characteristic.For x∈V（G）∪F（G），let d（x）denote the degree of x in G.A vertex（or face）of degree k is called a k-vertex（or k-face）.A vertex of degree at least k is called a k+-vertex.Let N（v）denote the set of neighbors of a vertex v in G.Two faces of a graph embedded in a surface are said to be adjacent if they share at least one common edge.A vertex v and a face f are said to be incident if v lies on the boundary of f.For x∈V（G）∪F（G），we use Fi（x）to denote the set of all i-faces that are incident or adjacent to x，and Vi（x）to denote the set of all i-vertices that are adjacent or incident to x.An edge xy with d（x）=i and d（y）=j is called an（i,j）-edge.For f∈F（G），we write if u1,u2,...,unare the boundary vertices of f in the clockwise order.A 3-face［u1u2u3］is called an（a1,a2,a3）-face if d（ui）=aifor i=1,2,3.

A graph G is said to be（3,1）∗-critical if G is not（3,1）∗-choosable，but every subgraph of G with fewer vertices is.Obviously，every（3,1）∗-critical graph is connected.Then，by Lih et al.［5］，the following lemma holds.

Lemma 1.1［5］If G is a（3,1）∗-critical graph，then the following facts hold.

（1）δ（G）≥3；

（2）There is no（3，3）-edge；

（3）There is no（3，4，4）-face.

Let Vi（or Fi）be the set of all i-vertices（or i-faces）of G，be the set of all 3-vertices of G that are not incident to any 3-face，and

Lemma 1.2If G is a（3,1）∗-critical graph without adjacent 3-faces，then

ProofBy Lemma 1.1（2）and（3），if a 3-vertex of G is incident to a 3-face，then this vertex must be adjacent to a 5+-vertex.For a vertex v∈V（G），d（v）≥5，let

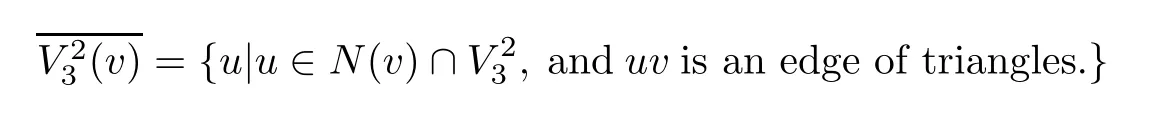
This completes the proof.

Lemma 1.3If G is a（3,1）∗-critical graph of nonnegative characteristic，then

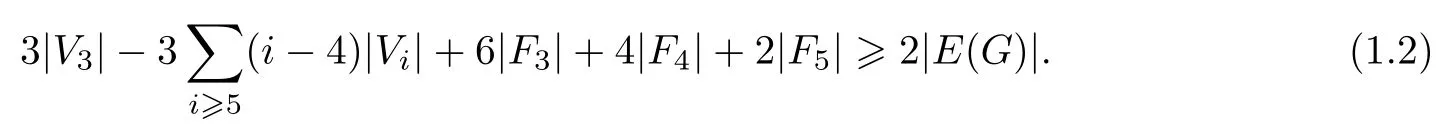
ProofBy the Euler-Poincare formula|V（G）|-|E（G）|+|F（G）|≥0,that is，

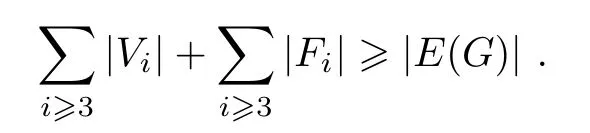
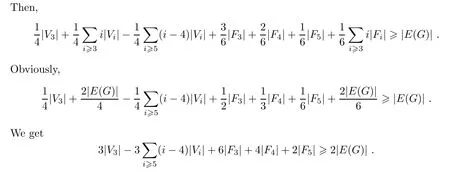
This completes the proof.

2　Main theorem

Let G be a graph embedded in a surface of nonnegative characteristic，we have the following main theorem.

Theorem 2.1If G is a 2-connected graph of nonnegative characteristic without 5-cycles，adjacent 3-faces and adjacent 4-faces，then G is（3,1）∗-choosable.

ProofSince G contains no 5-cycles，G contains no 3-cycles adjacent to 4-cycles.By G doesn't contains adjacent 3-vertices，adjacent 3-faces and adjacent 4-faces，then

［References］

［1］˘SKREOVSKI R.List improper colorings planar graphs［J］.Combinatorics Probability and Computing，1999（8）：293-299.

［2］EATON N，HULL H.Defective list colorings of planar graphs［J］.Bulletin of Institute Combinational Application，1999，25：79-87.

［4］˘SKREOVSKI R.List improper colorings of planar graphs with prescribed girth［J］.Discrete Mathematics，2000，214：221-233.

［5］LIH K W，SONG Z，WANG W，et al.A note on list improper coloring planar graphs［J］.Applied Mathematics Letters，2001，14：269-273.

［6］XU B G，YU Q.A note on（3,1）*-choosable toroidal graphs［J］.Utilitas Mathematica，2008，76：183-189.

［7］ZHANG L.A（3,1）*-choosable theorem on toroidal graphs［J］.Discrete Applied Mathematics，2012，160：332-338.

［8］CHEN Y Z，ZHU W Y，WANG W F.Improper choosability of graphs of nonnegative characteristic［J］.Computers and Mathematics with Applications，2008，56：2073-2078.

（责任编辑：李艺）

10.3969/j.issn.1000-5641.2016.02.007

非负特征图的列表不完全染色的研究

许洋

（青岛农业大学 理学与信息科学学院，山东青岛266109）

对每一个顶点v∈V（G），若任意给定k种颜色的列表，G都存在一个L-染色，使得G的每个顶点至多有d个邻接点与其染相同的颜色，则称图G为（k，d）∗-可选的.设G为可以嵌入到非负特征曲面的图.本文证明了若图G为2-连通的，且不包含5-圈、邻接的3-面和邻接的4-面时，G是（3，1）∗-可选的.

列表不完全染色；特征；圈；欧拉公式

2015-04

许洋，女，硕士，讲师，研究方向为图论及其应用.E-mail：xuyang 825@126.com.

O157.5Document code：A