一种海杂波背景下的目标跟踪数据关联方法
2016-11-11李亚安
陈 晓, 李亚安, 蔚 婧
(西北工业大学 航海学院, 陕西 西安, 710072)
一种海杂波背景下的目标跟踪数据关联方法
陈晓,李亚安,蔚婧
(西北工业大学 航海学院, 陕西 西安, 710072)
针对杂波背景下的目标跟踪问题, 采用最近邻滤波(NNF)算法和概率数据关联滤波(PDAF)算法对强海杂波背景下的水面舰船目标跟踪进行了理论分析与仿真。并针对密集海杂波环境, 在PDAF算法基础上引入二次距离加权概念, 对已有PDAF算法的关联概率值计算方法进行改进, 对不同密度的海杂波环境中的单目标跟踪进行了仿真。仿真结果表明, 该改进算法在密集海杂波环境中的跟踪性能有所提高, 能够更有效且可靠实现非机动目标的跟踪。
目标跟踪; 最近邻滤波(NNF)算法; 概率数据关联滤波(PDAF)算法; 海杂波环境
0 引言
利用雷达探测并跟踪水面舰船目标通常会受到海面杂波的影响[1]。海杂波的出现一方面干扰了雷达的正常工作, 使得雷达对水面目标的探测变得困难。另一方面, 密集海杂波会遮盖真实目标的回波, 导致雷达的探测、跟踪能力迅速下降。因此, 研究强海杂波背景下水面舰船目标的探测并跟踪具有重要的应用价值。
海杂波背景下水面舰船目标的探测和跟踪涉及到非平稳信号的检测和目标运动状态的估计。目标跟踪是信息融合的一个主要组成部分, 近年来在多个领域获得了广泛的关注, 一系列适用于目标跟踪的滤波和融合算法被相继提出。基于最近邻滤波(nearest neighbor filter, NNF)算法[2-4],提出了杂波环境下的目标跟踪算法——概率数据关联滤波(probabilistic data association filter,PDAF)算法[5-8]; 由于多目标跟踪的需要提出了联合概率数据关联算法[9-10]、多假设跟踪算法[11-12]及概率假设密度算法[13-14]等。在目标跟踪的融合算法方面, 最基本的关联算法为“最近邻”算法。该算法因计算简单, 实时性好, 在实际应用中获得了广泛关注, 其缺点是利用统计意义下的最近距离对目标进行状态更新, 在密集杂波环境下离预测位置最近的有效回波并不一定是目标的回波,从而导致误跟和失跟目标的。PDA算法考虑了关联门内的所有有效回波, 是用于杂波环境下单目标跟踪中较好的数据关联算法。但该算法忽略了有效量测和量测预测之间的关系, 在一定程度上扩大了量测噪声分布的随机性, 使得在后续的卡尔曼滤波过程中, 引起协方差矩阵的增大而导致跟踪门内落入更多的虚假量测值, 从而导致目标跟踪过程中出现误跟或者失跟现象。
针对杂波背景下的目标跟踪问题, 文中采用NNF算法和PDAF算法对强海杂波背景下的水面舰船目标跟踪问题进行了理论分析与仿真, 针对密集海杂波环境提出了利用距离加权的 PDA滤波算法, 对不同杂波密度下的跟踪算法进行仿真比较, 结果表明: 改进算法在一定程度上提高了密集杂波环境下的目标跟踪性能, 可更精确地实现密集杂波环境下的目标跟踪。
1 杂波环境下单目标跟踪问题描述
假设在海杂波环境中跟踪单目标, 每个离散时间间隔上得到的观测值都由若干个量测(如:真实目标回波、杂波)组成。设k时刻目标的状态向量为X(k ),则目标的运动模型
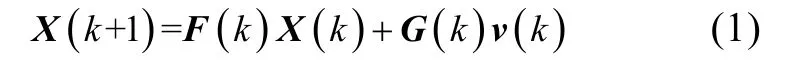
式中:F(k),G(k)分别为状态转移矩阵和噪声转移矩阵;v(k)是与目标初始状态统计独立的零均值高斯噪声向量,协方差矩阵已知。
得k时刻的测量方程

式中:H(k )为测量矩阵;w(k)为与所有其他噪声向量独立的零均值高斯噪声向量, 其协方差矩阵已知。在海杂波环境下, k时刻的量测集合可表示为, 其中, m表示量测数目。为前k次量测构成的累积集合。
在海杂波环境中, 由于量测的不确定性, 需要对量测和目标进行数据关联。数据关联的过程可以描述为, 利用某一算法确定跟踪门内的有效量测值来自于目标的概率, 从而实现目标状态的更新估计。
2 经典数据关联算法
2.1最近邻滤波算法
1973年Singer和Sea提出利用先验统计特性估计的最优跟踪滤波器, 即最近邻滤波器[2]。它的工作原理是利用跟踪门对量测数据进行门限过滤, 落入跟踪门的量测称为有效量测, 计算有效量测和目标预测位置之间的距离, 利用最近距离的有效量测对目标状态更新。其中跟踪门是目标跟踪空间中的一子区间, 中心位于被跟踪目标的预测位置, 跟踪门大小的设计保证以一定的概率接收有效量测, 落入跟踪门内的量测即作为有效量测, 即量测值 z(k+1)是否满足
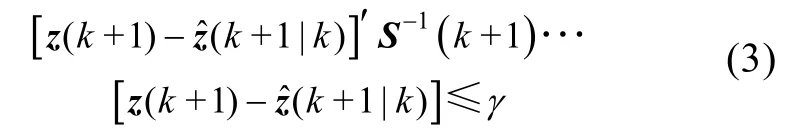
式中,S(k+ 1)表示k+1时刻的新息协方差矩阵,参数γ由χ2分布表获得。如果落入跟踪门内的有效量测只有 1个, 则该量测值直接被用于目标状态更新; 但若有多个量测值落在跟踪门内, 此时利用统计距离

使其达到最小的量测以用于在滤波器中对目标状态进行更新。NNF算法的优点是实时性好,计算量小且算法简单, 但在密集杂波环境下离目标预测位置最小的有效回波并不一定是目标的真实回波, 即NNF算法相关性能不完善, 可能出现所谓的误跟和丢失目标的情况。
2.2概率数据关联滤波算法
PDAF算法是一种全邻贝叶斯滤波算法[7],它考虑了落入跟踪门内的所有有效回波, 计算各有效量测来源于目标的概率, 然后利用关联概率值和有效量测对目标状态进行更新。该算法属于次优贝叶斯估计算法, 由于同时考虑了落入跟踪门内的所有有效量测, 因此该算法对杂波环境下的单目标跟踪出现误跟和失跟的概率较低, 计算量较小, 其滤波实现原理如下。
假设目标的状态方程和观测方程如式(1)和式(2)所示。目标起始完成后, 已知目标状态的估计和相应的协方差矩阵, 就可以预测下一个时刻目标的状态和量测。
k时刻落入跟踪门内的有效量测集合
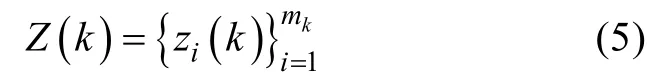
式中,Zk表示直到k时刻的所有有效量测的累积集合, 即

式中,mk为关联门内确认量测的数目。
以有效量测的累积集合Zk为条件,第i个有效量测zi(k)来自于目标的条件概率
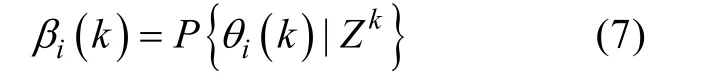
由事件定义可知, 所有事件是互斥的, 且是有限的, 所以, 则k时刻目标状态估计值
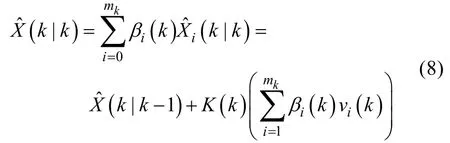
式中, vi(k)表示新息。
泊松杂波模型的参数化PDAF算法的关联概率
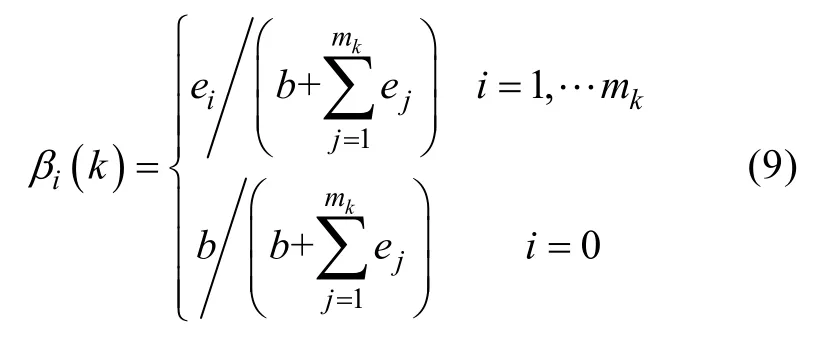
且

协方差更新为
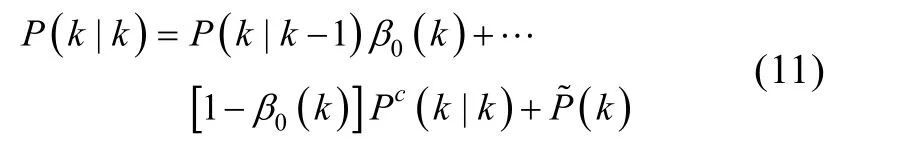
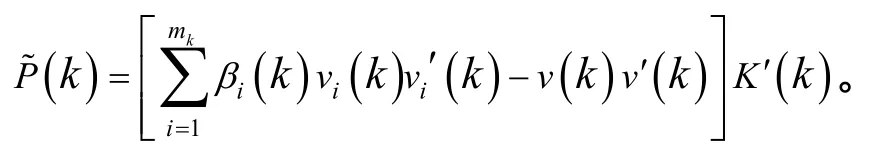
3 基于距离加权的PDAF算法
关联概率值是PDAF算法中的一个重要参数,它的计算结果直接影响着目标跟踪的性能。在目标跟踪过程中, 由于关联的不确定性, 会导致卡尔曼滤波协方差矩阵不断增大。
PDAF算法虽然是一种全邻滤波算法, 但也会使得这个问题加重, 而协方差的增大会导致更多的杂波落入跟踪门中, 这种恶性循环正是该算法有时误跟或者失跟的原因之一。
PDAF算法中的关联概率值分别来自于目标的正确量测概率和来自于杂波的虚假量测概率,但是没有明确有效量测和量测预测之间的关系,从一定程度上扩大了量测噪声分布的随机性。针对这一问题, 文献[15]通过对关联概率的距离加权将量测分布的先验信息明确的表达出来。但是该文献中的权值计算方法具有一定的局限性, 即当有效量测数为 1时(且有效量测为目标的预测值时), 权值会变为无穷, 从而导致滤波失败。此处对权值表达式做了一定的修改, 则k时刻有效区域内的第i个量测的权值
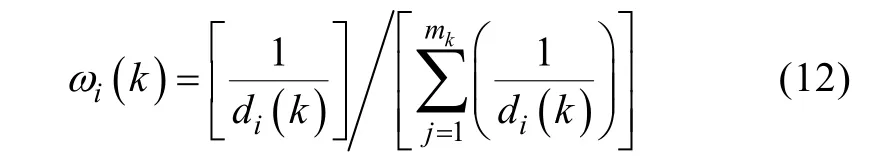
式中,di(k)是当前时刻第i个量测与预测中心之间的距离。用式(12)中的权值对关联概率进行修正, 可得修正后的关联概率
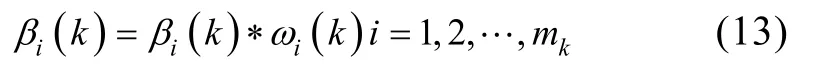
最后, 对关联概率进行归一化处理, 得
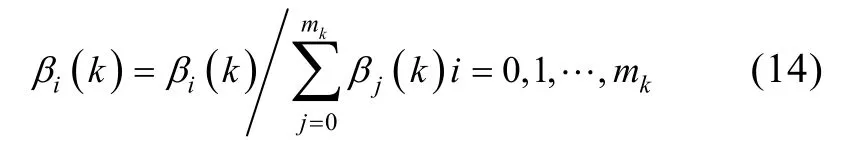
式(14)就是基于距离加权目标跟踪的关联概率值的计算公式, 利用距离加权对关联概率值进行改进, 对不同密度的海杂波环境下的目标跟踪进行仿真。
4 仿真结果与分析
4.1运动模型-CV模型
如果目标做匀速直线运动, 其运动状态可用匀速(CV)运动模型表示运动速度恒定, 取状态变量为,其中x和y表示目标不同运动方向的位置, 而x˙和y˙表示目标不同方向的速度。离散运动状态方程
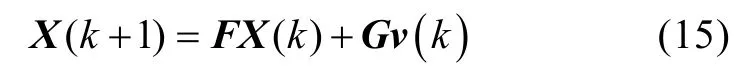
观测方程

4.2不同跟踪算法的仿真结果比较与分析
仿真1: 针对单目标匀速直线运动目标利用NNF算法和PDAF算法进行目标跟踪性能比较,仿真条件如上所述。
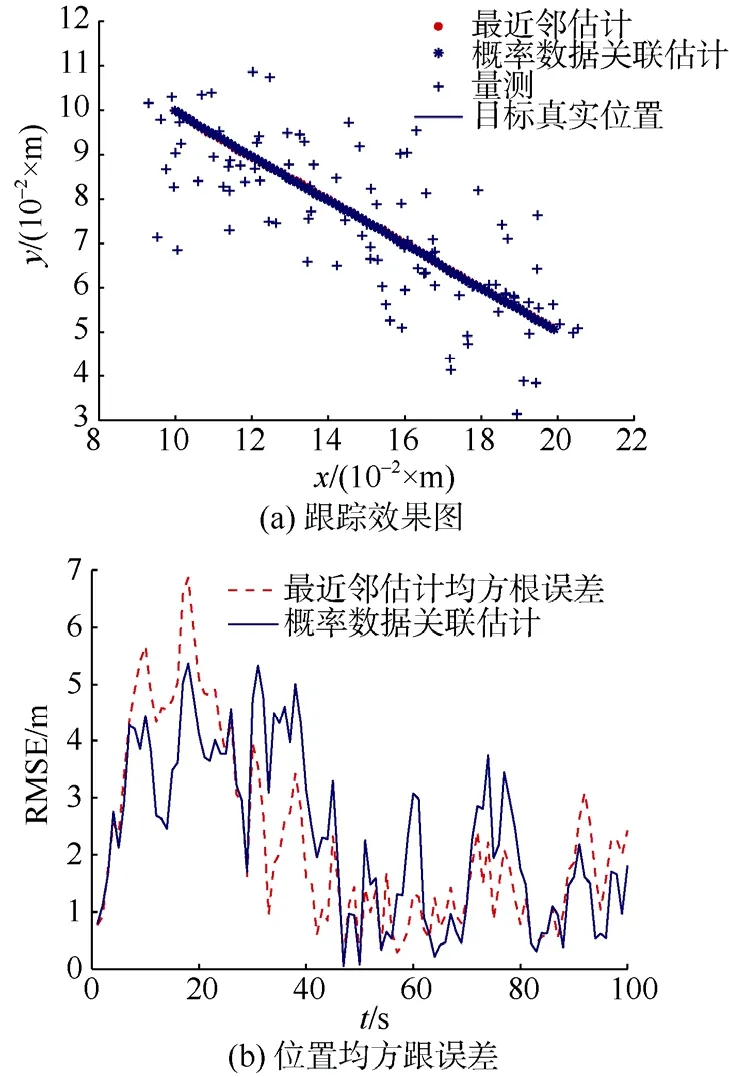
图 1 最近邻滤波器(NNF)算法与概率数据关联滤波(PDAF)算法跟踪比较(λ=1)Fig. 1 Tracking comparison between nearest neighbor filter(NNF) algorithm and probabilistic data association filter(PDAF) algorithm when λ=1

图2 NNF算法与PDAF算法的跟踪比较(λ=10)Fig. 2 Tracking comparison between NNF algorithm and PDAF algorithm when λ = 10
如图1所示, 在杂波密度λ=1时, 2种算法都可以成功实现高精度目标跟踪, 随着杂波密度的增大(如图2、图3所示), 2种算法的跟踪误差有所变大, 但PDAF算法跟踪效果好于最近邻滤波算法。因为NNF算法利用统计意义上与跟踪目标预测位置最近的有效回波对目标状态进行更新, 而杂波也有可能离预测位置最近, 这样就直接漏掉了正确的量测, 实际上, NNF算法忽略了虚假量测分布的随机性, 所以在密集杂波环境下该方法不适用。而PDAF算法利用关联概率值对落入跟踪波门内的有效回波进行加权, 得到等效回波,且利用有效回波对目标的状态进行更新, 所以在杂波环境下对单目标的误跟率较小。图中, 均方根误差用RMSE表示。

图3 NNF算法与PDAF算法跟踪比较(λ=50)Fig. 3 Tracking comparison between NNF algorithm and PDAF algorithm when λ=50
仿真2: 针对单目标匀速直线运动目标利用PDAF算法和改进PDAF算法进行目标跟踪性能比较, 仿真条件如上所述。
如图4所示, 在杂波密度1λ=时, 2种算法都可以成功实现单目标跟踪, 而且其跟踪误差差别很小, 但是随着杂波密度的增大(如图5和图6所示), 改进算法能够更快收敛到较小误差, 相对于PDAF算法, 误差有所降低, 当杂波密度再次增大时, 改进算法跟踪效果好于 PDAF算法, 从而在密集杂波环境中, 可以更好地实现高精度的目标跟踪。
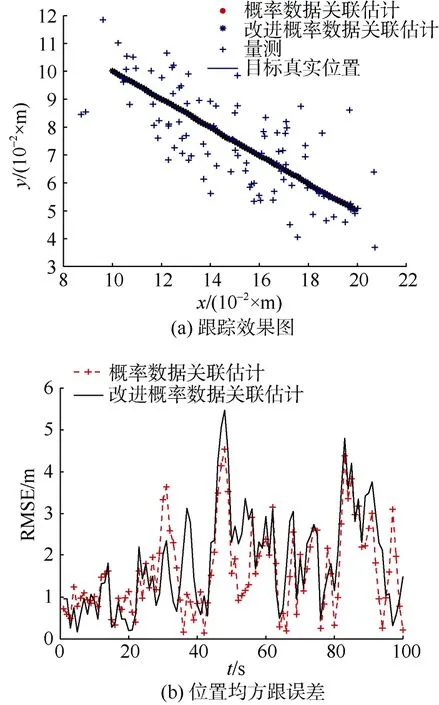
图4 PDAF算法与改进PDAF算法跟踪比较(λ=1)Fig. 4 Tracking comparison between PDAF algorithm and impro- ved PDAF algorithm when λ = 1
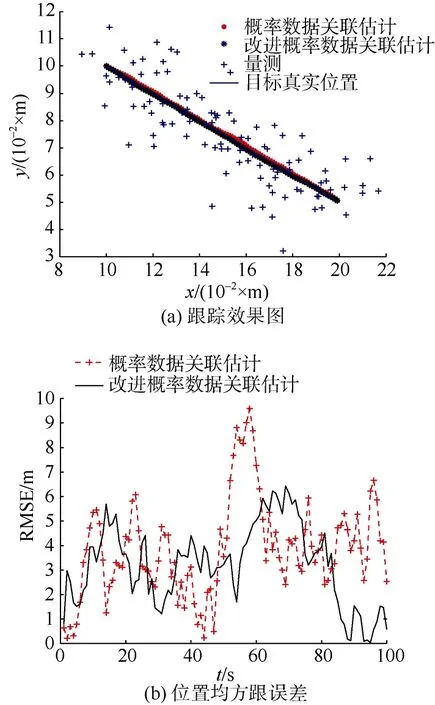
图5 PDAF算法与改进PDAF算法跟踪比较(λ=10)Fig. 5 Tracking comparison between PDAF algorithm and improved PDAF algorithm when λ=10
5 结束语
对于海杂波背景下的目标跟踪, 文中在对2种经典数据关联算法——NNF算法和PDAF算法理论研究的基础上, 针对杂波环境下非机动单目标跟踪进行了仿真研究, 并对其优缺点进行分析。同时在概率数据关联算法的基础上, 引入距离加权概念, 对关联概率值的计算进行二次加权处理, 提高了真假目标的关联概率, 通过对不同杂波环境下的非机动单目标跟踪进行仿真, 结果表明: 随着杂波密度的增大, 改进算法能够有效地提高目标的跟踪精度。文中对海杂波环境下非机动单目标的跟踪进行了仿真与分析, 为适应实际工程应用, 下一步需要对密集海杂波环境下的单机动目标的跟踪以及多目标的跟踪进行深入研究。
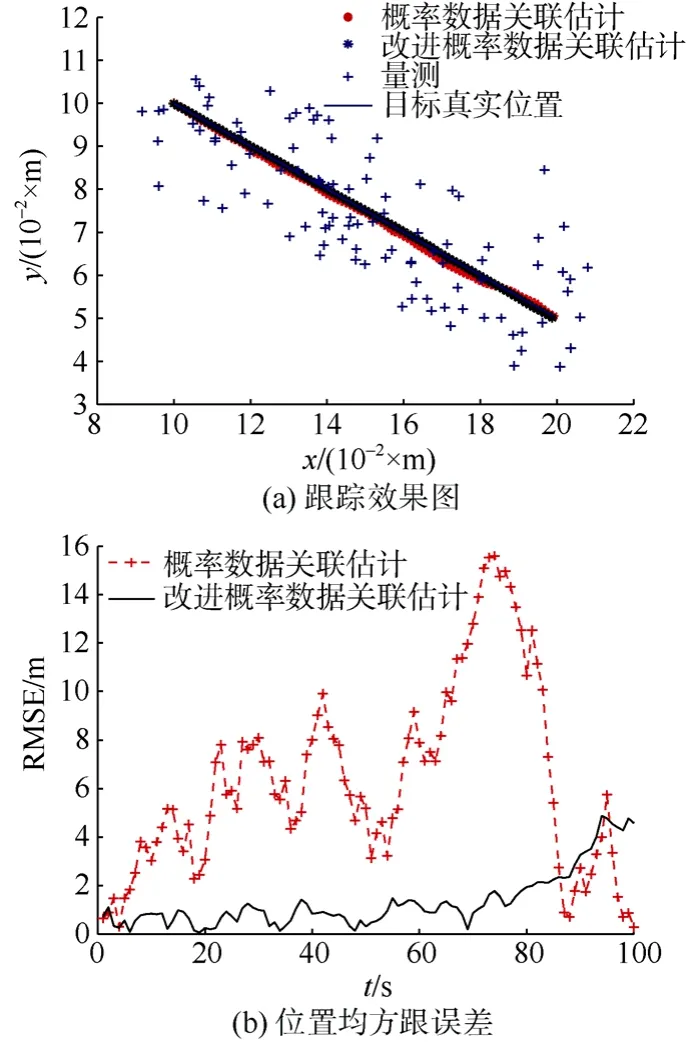
图6 PDAF算法与改进PDAF算法跟踪比较(λ=50)Fig. 6 Tracking comparison between PDAF algorithm and improved PDAF algorithm when λ=50
[1] 何友, 黄勇, 关键, 等. 海杂波中的雷达目标检测技术综述[J]. 现代雷达, 2014,36(12): 1-9. He You, Huang Yong, Guan jian, et al. An Overview on Radar Target Detection in Sea Clutter[J]. Modern Radar,2014, 36(12):1-9.
[2] Singer R A, Stein J J. An Optimal Tracking Filter for Processing Sensor Data of Imprecisely Determined Origin in Surveillance System[C]//Proceedings of the Tenth IEEE Conference on Decision and Control. Miami: Institute of Electrical and Electronics Engineers, 1971: 171-175.
[3] Lee D G, Song T L. Performance Analysis of NNF-class Target Tracking Algorithms Applied to Benchmark Problem[C]//5th Asian Control Conference, Melbourne: Institute of Electrical and Electronics Engineers, 2004: 1602-1607.
[4] Boumediene M, Ouamri A, Dahnoun N. Lane Boundary Detection and Tracking using NNF and HMM Approaches[C]//2007 IEEE Intelligent Vehicles Symposium. Istanbul: Institute of Electrical and Electronics Engineers ,2007: 1107-1111.
[5] Jaffer A J. Shalom Y B. On Optimal Tracking in Multiple Target Environments[C]//Proceedings of the Third Symposium on Non-Linear Estimation Theory and Its Applications. San Diego: Institute of Electrical and Electronics Engineers, 1972: 112-117.
[6] Boumediene M, Ouamri A, Dahnoun N, et al. Improved Kalman Filter Design for Three-dimensional Radar Tracking[J]. IEEE Transaction AES, 2001, 37(2): 727- 739.
[7] Kirubarajan T, Bar-Shalom Y. Probabilistic Data Association Techniques for Target Tracking in Clutter[J]. IEEE Proceedings of the IEEE, 2004, 92(3): 536-557.
[8] Bar-Shalom Y. Daum F. The Probabilistic Data Association Filter[J]. IEEE Control Systems Magazine, 2009, 29(6): 82-100.
[9] Shalom Y B, Fortmann T E. Tracking and Data Association[M]. Boston: Academic Press, 1988.
[10] Musicki D, Evans R. Joint Inregrated Probabilistic Data Assocation: JIPDA[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 1093-1099.
[11] Blackman S S. Multiple Hypothesis Tracking for Multiple Target Tracking[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 5-18.
[12] Ruan Y, Willett P. Multiple Model PMHT and its Application to the Second Benchmark Radar Tracking Problem[J]. IEEE Transactions on Aerospace and Electronic Systems,2004, 40(4): 1337-1350.
[13] Vo B N, Ma W K. Sequential Monte Carlo Methods for Multi-target Filtering with Random Finite Sets[J]. IEEE Transactions on Aerospace and Electronic Systems. 2005,41(4): 1224-1245.
[14] Mahler R. Multi-target Bayes Filtering Via First-order Multi-target Moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.
[15] Ni L Q, Gao S S, Xue L. Improved Probabilistic Data Association and Its Application for Target Tracking in Clutter[C]//2011 International Conference on Electronics, Communications and Control(ICECC). Ningbo: Institute of Electrical and Electronics Engineers, 2011: 293- 296.
(责任编辑: 杨力军)
A Method of Target Tracking Data Association in Sea Clutter Background
CHEN Xiao,LI Ya-an,YU Jing
(School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)
The problem of surface ship target tracking in strong sea clutter environment is theoretically analyzed and simulated by employing the nearest neighbor filter(NNF) algorithm and the probabilistic data association filter(PDAF) algorithm. Based on the PDAF algorithm, the concept of twice-weighted distance is introduced for the dense sea clutter environment to improve the correlation probability value calculation method of the existing PDAF algorithm, and the single target tracking in the sea clutter environment with different densities is simulated. Simulation results show that the improved algorithm can improve the tracking performance in dense sea clutter environment, hence realize the non-maneuvering target tracking more effectively and reliably. This research may provide reference for accurate tracking of surface ship targets in sea clutter background.
target tracking; nearest neighbor filter(NNF) algorithm; probabilistic data association filter(PDAF) algorithm;sea clutter environment
TJ630.34; TB566
A
1673-1948(2016)05-0334-06
10.11993/j.issn.1673-1948.2016.05.004
2016-06-29;
2016-07-22.
国家自然科学基金(51179157, 51409214); 陕西省自然科学基础研究计划(2016JQ6071).
陈晓(1986-), 女, 在读博士, 研究方向为水下目标跟踪及水声信号处理.
