基于信噪比优化的中段传感器预指派模型
2016-11-11杨媛媛盛卫东张寅生
杨媛媛,盛卫东,安 玮,张寅生,江 丹
(国防科技大学电子科学与工程学院,湖南 长沙 410073)
·工程应用·
基于信噪比优化的中段传感器预指派模型
杨媛媛,盛卫东,安玮,张寅生,江丹
(国防科技大学电子科学与工程学院,湖南 长沙 410073)
结合中低轨中段弹道目标连续跟踪这一特殊应用背景,从跟踪相机交接的再捕获确认到稳定跟踪的全程角度出发,提出了一种基于信噪比和跟踪精度联合优化的新的传感器预指派模型。并采用通过对粒子降维处理和位置矢量更新的实值粒子群优化算法,对所提模型的性能进行分析和比较。仿真实验表明,该模型的调度性能较之前的优化目标函数及二进制粒子群优化算法,更贴近导弹中段飞行情况的实际且性能有所改进,因而是一种更高效的调度模型。
信噪比优化;多传感器管理;实值粒子群优化;目标连续跟踪
0 引言
空间跟踪与监视系统(STSS)能够有效弥补天基红外系统(SBIRS)和地面预警雷达对中段弹道目标的观测缝隙,是实现对中段弹道目标探测的重要手段[1]。系统中传感器的优化调度是其亟待解决的重点问题之一,即在合理的时机、调用合适的凝视型相机、指向合适的空域,实现对目标的协同探测,从而最有效地完成系统任务。其本质是一个非线性最优化问题,即根据一定的准则,建立一个易于量化的目标函数,再加上传感器资源的约束条件,然后对目标函数进行优化以获得传感器对目标的有效分配[2]。
传感器调度研究主要集中在两方面:一是建立能反映应用特点的传感器优化调度模型,二是寻求合适的传感器调度模型求解方法。在传感器调度建模方面,王博等人提出了一种以目标跟踪精度作为优化目标的中段预指派传感器调度方法[3-4],在目标跟踪精度和计算时效性方面均具有较好的性能,其不足是缺乏对每一次调度引起的目标重捕获过程的考虑,而重捕获失败大大增加了目标交接丢失的风险。在该文献的基础上,本文不仅考虑了目标跟踪精度,还重点分析了影响目标重捕获性能的约束条件,建立了一种基于信噪比优化的中段传感器预指派调度模型,以兼顾目标重捕获性能和目标跟踪精度。在模型求解上,本文采用实值粒子群优化(RPSO)方法,通过降低粒子的维数和改进实值粒子群优化的位置更新式来减少运算量。仿真结果验证了本文方法的有效性。
1 基于信噪比优化的中段预指派模型
从中段传感器优化调度的角度,必须同时考虑目标重捕获和锁定跟踪两方面。
1.1目标重捕获阶段的约束分析
目标重捕获,是指在传感器调度过程中捕获传感器与跟踪传感器或者跟踪传感器与跟踪传感器交接过程初期对于导弹目标再次捕获成功的过程,是一个对目标空间截获、时间截获和能量截获的综合作用的过程,影响因素多。本文主要考虑目标能量截获的影响。目标能量截获与目标辐射强度、背景特性、载荷探测性能、接力传感器对目标的观测视角和探测距离、太阳/月亮杂散光等因素有关。本文拟采用目标信噪比衡量目标能量截获的影响,建立一种基于目标信噪比的重捕获优化函数。
1)信号
星载红外探测系统中,由辐射源到电压/电流的信号传输链[5]如图1所示。

图1红外系统信号传输链
由于目标距离卫星很远,其在传感器焦平面上属于“点”目标。在默认像元面积、光学系统焦距为1的情况下,点目标在探测器焦面上产生的电子数为:
N=(Aoτint/(hc))∫(I/R2)λητdλ
(1)
式中,Ao为光学系统入瞳面积,τint为积分时间,h为普朗克常数,c为光速,I为目标光谱辐射强度,R为距离,η为量子效率,τ为系统透过率。
2) 噪声
星载红外凝视探测系统的噪声主要包括背景噪声、杂散光、热噪声、读出噪声等。
①背景噪声
背景噪声是由探测器所观测的背景环境入射至探测器而形成的。在STSS系统中,根据传感器调度结果的不同,对目标的探测面临三种背景情况,具体如图2所示。

图2 传感器指向与背景类型示意图
图2中卫星在高度为H的轨道上飞行,地球半径为R,图中深灰色区域为云层,设其高度为h1,浅灰色区域为地球外层大气,设其高度为h2,跟踪传感器的指向设为Pt,在星体坐标系下俯仰角为e,其视场角为δ,可计算出跟踪传感器视场的范围,以视线切线高度h来表示,假定目标导弹T出现在凝视相机的视野中,可以根据视线的切线高度h得知其对应的背景类型:
(2)

②杂散光
杂散光是由月球、太阳等外部辐射源经过传感器遮光罩而进入探测器而形成的。特别是当被调度的传感器与月球、太阳的观测角过小时,杂散光可能导致传感器“致盲”甚至烧毁。这是由于太阳光直射入光学系统视场会使得跟踪传感器红外探测阵列饱和,难以探测到目标。为避开太阳直射光影响,跟踪传感器对目标探测应满足如下条件:
卫星在地影本影区内,没有日光可以到达卫星,此时对目标探测不受太阳影响;
卫星不在地影本影区内,日光可到达卫星,此时要保证星日矢量与传感器光轴的夹角ω大于太阳对跟踪传感器探测产生影响的临界角ωcri。
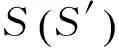
(3)

图3 太阳对跟踪传感器覆盖性能的影响
更进一步地分析,当ω>ωcri时,具体的杂光抑制要求为太阳辐射在工作波段内到达探测器表面的辐照度不高于传感器噪声等效辐照度,据文献[7]得红外传感器噪声等效辐照度ENEI为2.17×10-11W/cm2。
定义传感器系统的太阳辐射杂光抑制比为:
(4)
式中,Ed(ω) 为太阳辐射与光轴夹角为ω时入射到传感器像焦面的辐照度;E0为太阳辐射在工作波段的辐照度。对于3~5 μm的工作波段:
E0=2.17×10-11
且系统要求杂光抑制比R(ω)的量级为10-8,可解得30°为太阳规避角,即临界角ωcri,即要求ω>30°。
③热噪声
热噪声是探测器内电子的无规则运动引起的噪声,为:
(5)
式中,T为探测器的绝对温度,q为电荷量,R0为有效负载电阻。
④读出噪声
读出噪声描述了从焦面电子到放大电流到A-D转换整个过程中所有的电子学噪声[6],为:
(6)
式中,vro为探测器的读出噪声电压,Cint为探测器的等效积分电容。
因此,可以得出系统总噪声大小为:
(7)
因此,信噪比为:

(8)
约束条件为:太阳、月亮约束角必须大于某角度,否则相机损害;SNR必须大于某值,否则目标丢失。
1.2目标锁定跟踪阶段的约束分析
目标锁定跟踪阶段是指传感器交接重捕获成功后,保持高的立体跟踪精度稳定跟踪的过程,这一阶段是资源约束、任务约束和时间约束综合作用的过程,本文主要考虑传感器跟踪性能、传感器预期跟踪时长、卫星与目标的几何关系等约束条件,拟建立一个对跟踪精度与预期跟踪时长进行线性加权的优化函数。
在低轨红外预警星座中,对目标进行立体定位至少需要两颗卫星,从每颗卫星获得二维像平面观测,由四个观测方程组成观测方程组以求解目标的三维位置[8]。本文采用文献[8]考虑位置测量误差、欧拉角测量误差和像平面测量误差得出的目标跟踪精度,为:
(9)
1.3兼顾重捕获和跟踪精度优化的中段预指派模型
预指派实际上是对传感器资源进行静态管理调度,需要从目标预测轨迹全程角度考虑管理方法。本文首先从时间上对目标自由段预测轨迹进行量化;然后以所有量化步长的平均指标最小化作为预指派的优化目标,并建立预指派模型。对目标自由段预测轨迹的量化就是指以一定的步长将目标预测轨迹分为时长相等的若干段,如图4所示。

图4 目标预测轨迹量化

(10)
中低轨红外预警星座传感器预指派的目的就是从中段全程跟踪角度出发,力求给出一个高跟踪精度、高资源利用率且满足调度约束条件的传感器预指派方案。考虑到每一量化步长对目标可实现有效覆盖的虚拟传感器是不断变化的,因此预指派就是从某量化步长的备选传感器集合中选择若干个传感器对目标进行处理,是一个约束最优化问题,假定矢量集A=(A1,A2,…,AN)表示每一量化时段所选择的传感器组合,其选择由优化函数求解最优值决定,调度流程为:
步骤1:设初始步长τ=1,初始化矢量集A中各传感器资源当前的工作状态(关机或者正在跟踪目标);
步骤2:分别计算集合A1中各传感器组对估计目标的GDOP,并从中选出最优(GDOP最小)的元素Si(仅限于传感器的两两组合);
步骤3:分别计算集合A1中各传感器组对估计目标的SNR,并从中选出最优(SNR最大)的元素Sj(组合仅由单个传感器组成,因为当观测卫星数目大于2时,对目标跟踪精度的提高没有太大贡献);
步骤4:若Sj⊂Si,则选择Si进行调度,否则选择Sj∪Si进行调度;
步骤5:整理保存本步长预分配的调度结果及各目标的跟踪状态,τ=τ+1;
步骤6:当τ>tbal/Δt时,调度完毕。
2 基于实值粒子群优化的传感器调度求解方法
传感器的工作状态有两种,即等待状态和处理状态。假定第m个粒子的N维位置矢量可以表示为:
(11)

但考虑到采用BPSO算法进行传感器管理调度时各粒子的位置矢量均为1×N稀疏矩阵,存在冗余运算。为进一步降低运算量,提高传感器管理算法的性能,本文采用一种基于RPSO的传感器管理算法。
假定sij=1表示第i个传感器分配给第j个目标,sij=0则不存在这种分配关系。在传感器和目标的优化分配中,同时分配给每个目标的传感器个数都有一定限制,这种限制主要有以下两种:



3 仿真实验分析
星座轨道参数取28/4/2/1596/77.8[5](表示该星座共4个轨道面,每轨道面7颗卫星,轨道高度1596km,轨道倾角77.8°,相位因子为2)。目标参数如表1所示。
仿真时预测弹道的量化步长取50s,传感器观测间隔为1s,视线测量误差90μrad。仿真实验在配置为Cuo2 E8400 CPU、4G内存的台式机上进行,共50次Monte Carlo实验。
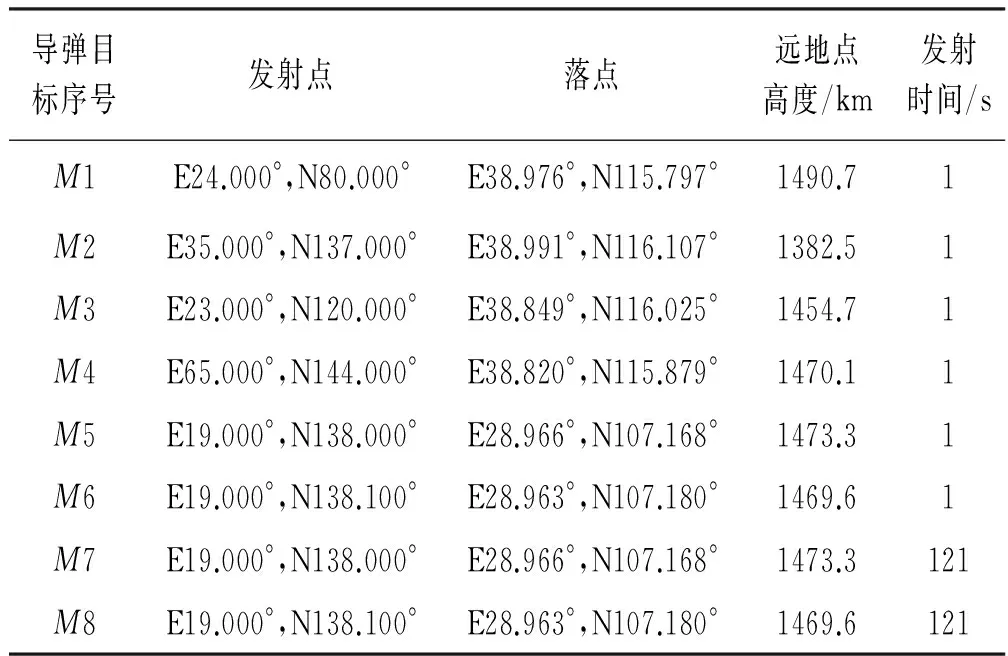
表1 目标参数
其次,对本文提出的中段传感器调度算法进行仿真验证,并与文献[10]进行对比。经多次统计的跟踪误差、计算耗时、目标重捕获丢失率等情况如图5、图6和表2、表3所示。

图5 以跟踪精度为优化函数的位置速度误差

图6 以信噪比为优化函数的位置速度误差

传感器调度优化函数GDOPSNR+GDOP预指派平均运算时间/s22.3732.11

表3 各调度方法目标丢失率
4 结束语
在基于跟踪精度的传感器预指派模型的基础上,本文结合中低轨天基传感器网络卫星和目标运动实际,提出了一种再捕获过程基于信噪比优化函数的调度模型。仿真结果表明,基于SNR、GDOP优化函数的传感器预指派模型虽然较单纯的GDOP优化函数调度计算耗时有所增加,但目标丢失率却显著降低,这一点从全预警星座效能的角度来说更具优势。本文提出的优化函数在目标跟踪位置(速度)误差上也有一定程度的改进。但该方法存在如下局限:模型在自由段目标跟踪初始阶段需要较长的调度计算时间且仅适用于目标不存在机动的情况,而对于存在机动的情况,则需采用实时调度方法;另外目标丢失率的降低对场景有着较强的选择性,此模型的普适性还需进一步研究。■
[1]武立华,盛卫东,安玮.一种基于单站仅测角观测的弹道射向估计[J].航天电子对抗,2012,28(5):44-46.
[2]Blackman S,Popoli R. Design and Analysis of Modern Tracking Systems[M]. Boston London:Artech House,1999:967-1065.
[3]王博,周一宇.低轨红外预警星座传感器资源调度算法研究[DB].硕博全文数据库,2010.
[4]王博,许丹,安玮,等.低轨星座传感器实时调度模型[J].应用基础与工程科学学报,2011(2):335-344.
[5]Cantella MJ.The infred&electro-optical systems handbook[M].Washington USA:SPIE Press,1993:159-205.
[6]陈维真,张春华,周晓东.空间目标的光度特性及其成像信噪比研究[J].红外技术,2007,29(12):716-719.
[7]牛金星,周仁魁,刘朝晖,等.天基红外探测系统的杂散光分析与计算[J].光学学报,2010,30(3):768-771.
[8]王博,周一宇,鲁建华,等.基于实值粒子群优化STSS系统传感器管理算法研究[J].系统仿真学报,25(7): 1135-1140.
[9]Jin N,Rahmat Y.Advances in particle swarm optimization for antenna designs:Real-Number,binary,single-objective and multiobjective implementations[J].IEEE Trans. on Antennas and Propagation,2007,55(3):556-567.
[10]王博,盛卫东,安玮,等. 基于粒子群优化的传感器预分配方法[J].信号处理, 2009,25(7):1135-1140.
Midcourse sensor pre-assignment model based on SNR optimization
Yang Yuanyuan, Sheng Weidong, An Wei, Zhang Yinsheng, Jiang Dan
(College of Electronic Science and Engineering,National University of Defense Technology, Changsha 410073, Hunan ,China)
Based on a special application background of continual midcourse object tracking, a novel sensor pre-assignment model based on SNR optimization combined the GDOP optimization model is proposed according to the whole course from the capture affirmance to the stable tracking. Furthermore, real-number particle swarm optimization is adopted that through dimensionality reduction and position vector improvement, and the proposed model is analyzed and compared in detail. The simulation results show that the optimization model is a more efficient algorithm compared with the optimized objective function and binary particle swarm optimization algorithm.
SNR optimization;multi-sensor management;RPSO;object continue tracking
2016-02-23;2016-04-14修回。
杨媛媛(1992-),女,硕士研究生,主要研究方向为多传感器管理调度。
TN97
A
