加速退化下光伏组件伪失效寿命分布估算

刘桂雄，余荣斌，徐　欢

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.广东产品质量监督检验研究院，广东 广州 510330)



加速退化下光伏组件伪失效寿命分布估算

刘桂雄1*，余荣斌1，2，徐欢1

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.广东产品质量监督检验研究院，广东 广州 510330)

开展了加速退化条件下光伏组件产品可靠度评估的研究，提出了新型的基于GLD的光伏组件的伪失效寿命分布估算方法。首先， 利用可决系数检验法(R2)优选最佳加速退化轨迹，得到样本组伪失效寿命值。然后，应用Bootstrap法产生自助样本扩充样本群，构建基于GLD的伪失效寿命分布模型，该模型无需预设先验分布，即可真实反映不同加速条件下光伏组件伪失效寿命分布形态。最后，以18 W小功率Mono-Si单晶硅光伏组件加速性能退化数据为例，估算了光伏组件在加速退化条件下的伪失效寿命分布和可靠度。结果表明：在加速退化条件下，本文方法得到的可靠度曲线与试验数据拟合结果很好，绝对误差基本在±300 h内，相对误差不超过±15%，满足工程预测精度需求。

光伏组件；加速退化；伪失效寿命；GLD分布；可靠度评估

1　引　言

对于高可靠性、长寿命的产品，可通过性能退化数据来对产品进行可靠性评估[1-3]，但由于时间、成本等方面的限制，往往难以获取足够的自然退化数据，开展基于加速退化的寿命预测方法研究成为解决其质量可靠性评估问题的重要途径[4-5]。目前加速退化数据寿命预测方法主要有退化量分布法、伪失效寿命法等。退化量分布法通过拟合各个时刻样本性能退化数据分布，估计分布参数随时间变化规律，建立退化模型来对预期寿命进行预测，方法简单，但需要样本各时刻退化数据服从相同分布形态前提条件，给实际应用带来不便；伪失效寿命法通过曲线拟合退化数据，预测产品伪失效寿命来对产品进行可靠性评估，其关键在于获取伪失效寿命分布，较好的反映伪失效寿命分布形态。Lu&Meeker首先建立了一般化非线性综合效应模型的伪失效寿命描述方法，但要求同一个样本族样品伪失效寿命分布形态相同[6]；文献[7]计算了不同加速应力下LED灯具的可靠度，但需预设伪失效寿命可能的分布形式并对其进行分布假设检验；文献[8-11]分别介绍了近年来在伪失效寿命法研究成果，但需一定数量样本及较多测量时刻，且必须预先假设伪失效寿命数据应服从某种特定分布。而在光伏组件可靠性评估方面，它作为光伏系统的核心部件，属于高可靠性、长寿命产品，其质量可靠性将直接关系到光伏电站发电效率以及电站使用寿命，目前国内外开展光伏组件性能退化可靠性评估研究较少，文献[12]提出了一种Atlas25plus光伏组件可靠性综合测试方案，本团队在文献[2]中研究了基于β分布统示法的光伏组件性能退化可靠度估算方法，但基于加速退化的光伏组件可靠度方法研究未见报道。为此，本文针对光伏组件产品加速退化条件下可靠度评估，研究了一种基于GLD的光伏组件伪失效寿命分布新型估算方法。

2　基于加速退化的光伏组件伪失效寿命分布估算

基于GLD的光伏组件伪失效寿命分布新型估算方法是利用R2(可决系数检验法)优选最佳加速退化轨迹，外推样本伪失效寿命值，无须假设退化轨迹满足相同形式要求；应用Bootstrap法产生自助样本扩充样本群，改善小子样下分布估算准确性问题；构建基于GLD的伪失效寿命分布模型无需预设先验分布，较好地反映出不同加速条件下光伏组件伪失效寿命分布形态。以18 W 单晶硅光伏组件加速退化数据为例估算光伏组件加速退化条件下伪失效寿命分布，也验证了该方法的有效性。图1所示为基于加速退化的光伏组件伪失效寿命分布估算流程图。

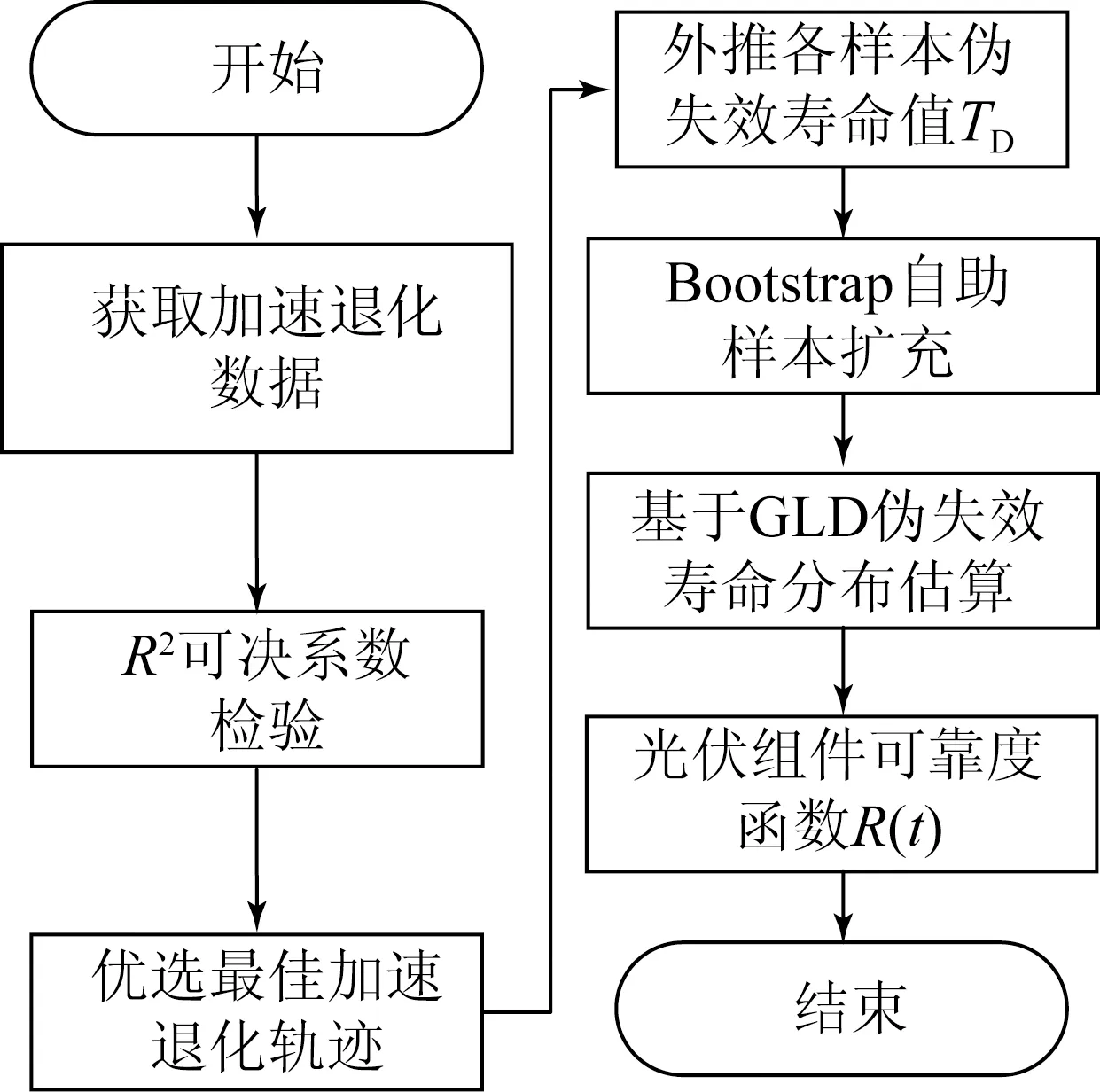
图1　加速退化下光伏组件伪失效寿命分布估算

Fig.1PV modules pseudo-failure lifedistribution estimate based on accelerated degradation data

2.1最优加速退化轨迹选取

加速退化轨迹描述设定加速条件下产品退化规律或失效过程，当不存在先验退化模型或因产品内在失效机理复杂无适当经验模型可用时，根据退化数据拟合退化轨迹是建立产品退化模型、评估可靠度的基础。产品退化轨迹可包括线性、凸形和凹形3种变化趋势，但考虑到很多常见的非线性退化轨迹(如凸形、凹形等)经过一定的变换之后都可以转化为线性轨迹，故研究重点多集中于线性轨迹的回归分析方法。

设fk(x)为第k个线性无关的确定函数，αk为回归参数，ε为随机误差，且有∑ε=0，则线性轨迹回归方程的一般表达式可描述为：

α0+α1X1+…+αn-1Xn-1+ε.

(1)

设获取加速退化数据Y=[y1y2…yn-1]T，α=[α0α1…αn-1]为待评估回归参数，ε=[ε0ε1…εn-1]为随机误差向量，服从标准正态分布，X为对应回归变量x构成变换函数fk(x)矩阵，则式(1)可以写成：

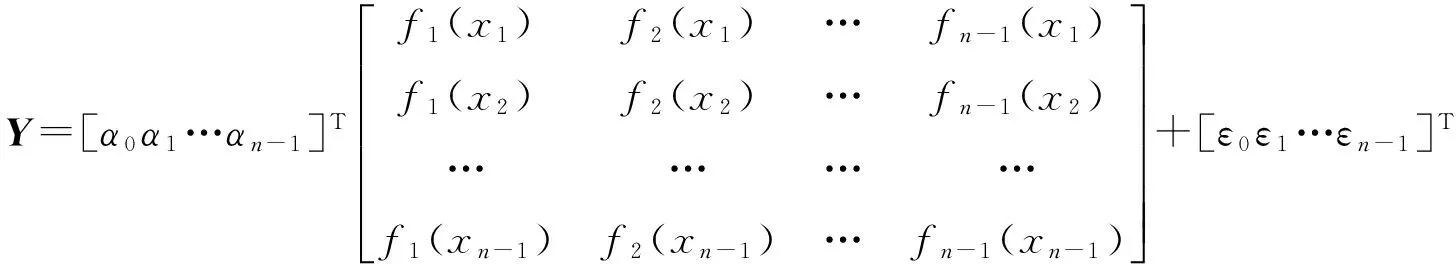
(2)

采用最小二乘估计法求得α、ε的估算值：

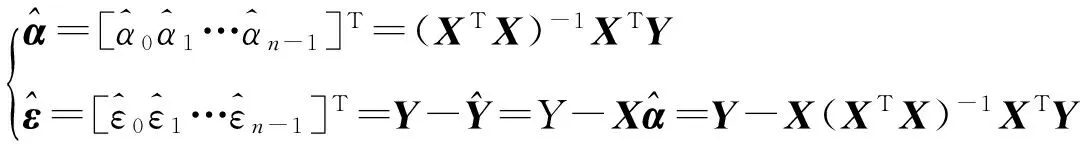
(3)

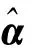
(4)

(5)

R2值反映回归方程中随机误差项对因变量影响程度，R2值越大，自变量对因变量影响程度越大，拟合效果也越好，则R2值最大的回归方程形态即为最优加速退化轨迹模型。

2.2Bootstrap自助样本扩充

由于试验成本、测试周期等方面原因，往往难以投入大量样本进行长时间试验，导致样本集TD容量偏小(小子样n<30)，故须考虑小子样条件下伪失效寿命分布预测准确性问题。

设样本观测数据X=(x1，x2，…，xn)服从某未知总体分布F，Fn为观测数据的经验分布函数，则Bootstrap法自助扩充步骤为[13]：

①将观测数据X=(x1，x2，…，xn)按从小到大顺序排列，可到X′ =(x(1)，x(2)，…，x(n))(x(1)≤x(2)≤…≤x(n))，令k=1，2， …，n-1，则由新统计量X′构造原样本经验分布函数：

(6)

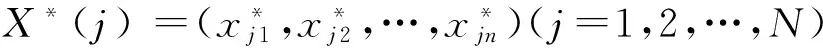
2.3基于GLD的光伏组件伪失效寿命分布估算

自助样本扩充能在保持与原样本总体分布特征一致前提下有效增加样本信息量，实现小子样“增量增息”，但总体分布形态仍为未知。当进行光伏组件伪失效寿命分布估算时，会面临难以获取其伪失效寿命先验分布而无法对其分布形态进行预设。提出一种基于GLD统示法的光伏组件伪失效寿命分布估算方法，在自助样本扩充基础上利用GLD统示法构建光伏组件伪失效寿命分布模型，无须预设先验分布。

若光伏组件伪失效寿命预测值TD服从GLD即广义λ分布，其分位数函数为Q(y)，y∈[0，1]，则TD=Q(y)产生一个随机变量：

Q(y)=λ1+[yλ3-(1-y)λ4]/λ2(0≤y≤1)，

(7)

其中：λ1、λ2为定位参数、尺寸参数，λ3、λ4为形状参数，则其概率密度函数表达式为：

(8)

与β统示分布类似，广义λ分布同样具有多态性，无须预设特定分布形态，合乎数据真实分布特性；但GLD具有拖尾性，较β分布更适于寿命分布的直接拟合[14-15]。此外，广义λ分布可用分位数函数进行定义，而分位数函数为寿命分布函数的反函数，便于建立与分布函数之间的关系，适合拟合寿命预测数据。

设μ代表均值，σ2代表方差，γ3代表偏度，γ4代表峰度，则广义λ分布的四阶距αk(k=1，…，4)可表示为：

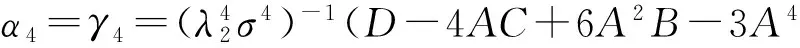
(9)

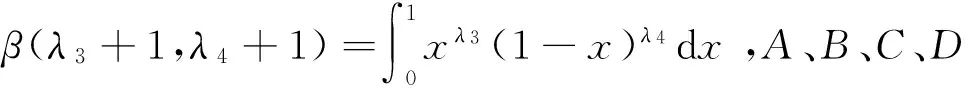
(10)

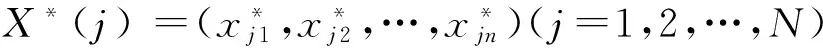
(11)

(12)

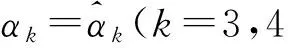
(13)

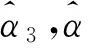
最后将求得参数λ1，λ2，λ3，λ4代入式(7)、(8)可得到GLD分位数函数及其概率密度函数表达式。

3　应用实例

为验证方法的有效性，向某光伏制造商定制了一批18 W小功率Mono-Si单晶硅光伏组件，每块组件由4片电池片连接封装而成，表1所示为试验用Mono-Si单晶硅组件样品典型规格参数。

表1　Mono-Si单晶硅组件样品典型规格参数

(a)ATLAS SEC2100试验箱(a)ATLAS SEC2100chamber(b)老化试验样品接线图(b)Sample wiring ofaging test

(c)Halm-cetisPV测试系统(c)Halm-cetisPV　(d)STC输出功率测试图(d)STC output power test

加速退化试验系统由全光谱耐候性老化试验箱ATLAS SEC2100、光伏组件模拟器测试系统halm-cetisPV组成。图2所示为试验设备及样品接线图。

Mono-Si单晶硅组件分为5块/组进行加速退化试验，每组样品试验时间为1 000 h，每隔100 h 取出放入光伏组件模拟器测试系统依据IEC61215-2005进行STC下输出功率Pd测试[16]。各组试验加速应力参数设置及试验顺序如表2所示。

表2　各组试验加速应力参数设置及试验顺序

表3所示为Mono-Si单晶硅组件输出功率Pd加速退化试验数据结果。首先利用表3加速退化数据进行线性回归拟合并优选最佳退化轨迹，曲线拟合及优选预测结果如表4所示。

表3　Mono-Si单晶硅组件输出功率Pd加速退化试验数据

表4　光伏组件最优退化轨迹模型及伪失效寿命预测

可以看出，由于样本伪失效寿命估测集TD容量偏小(小子样n<30)，直接按伪失效寿命法进行寿命分布拟合会带来较大误差，需在保持与原样本总体分布特征一致前提下有效增加样本信息量，实现小子样的“增量增息”。以试验序号①样本组为例，由于样本伪失效寿命估测集TD={x1，x2，…，xn}(n=5)为小子样，应用Bootstrap自助法对小字样进行扩充，重复抽样m=100，扩充后自助样本矩阵Xmn：

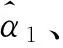
同理，可求得表5其它各样本组λ分布参数，将各组λ分布参数代入式(4)可得概率密度函数f(x)，见图3光伏组件伪失效寿命λ分布概率密度函数。

表5　光伏组件各样本组伪失效寿命λ分布参数

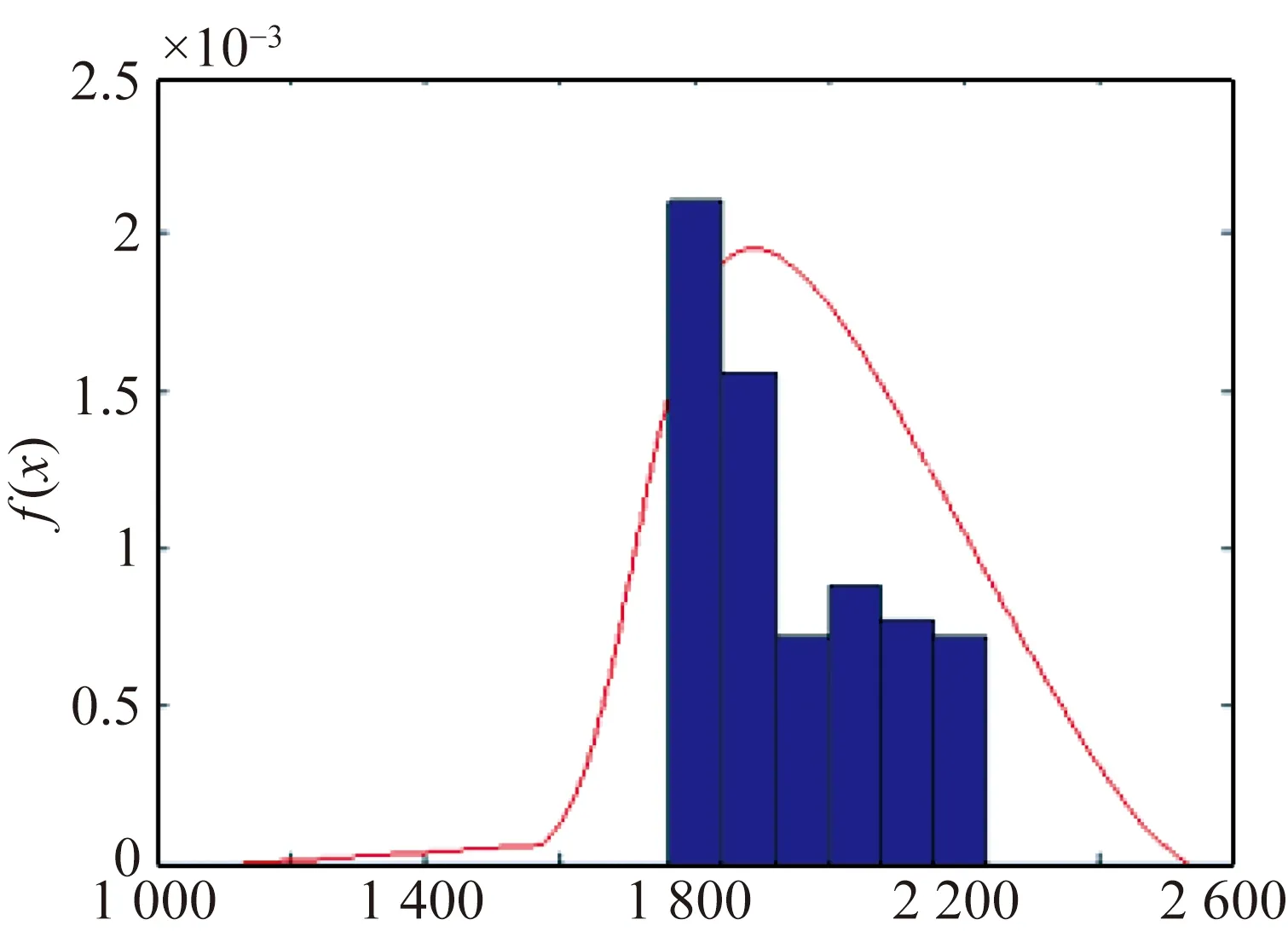
(a)试验序号①(a)Testsequence①

(b)试验序号②(b)Testsequence②

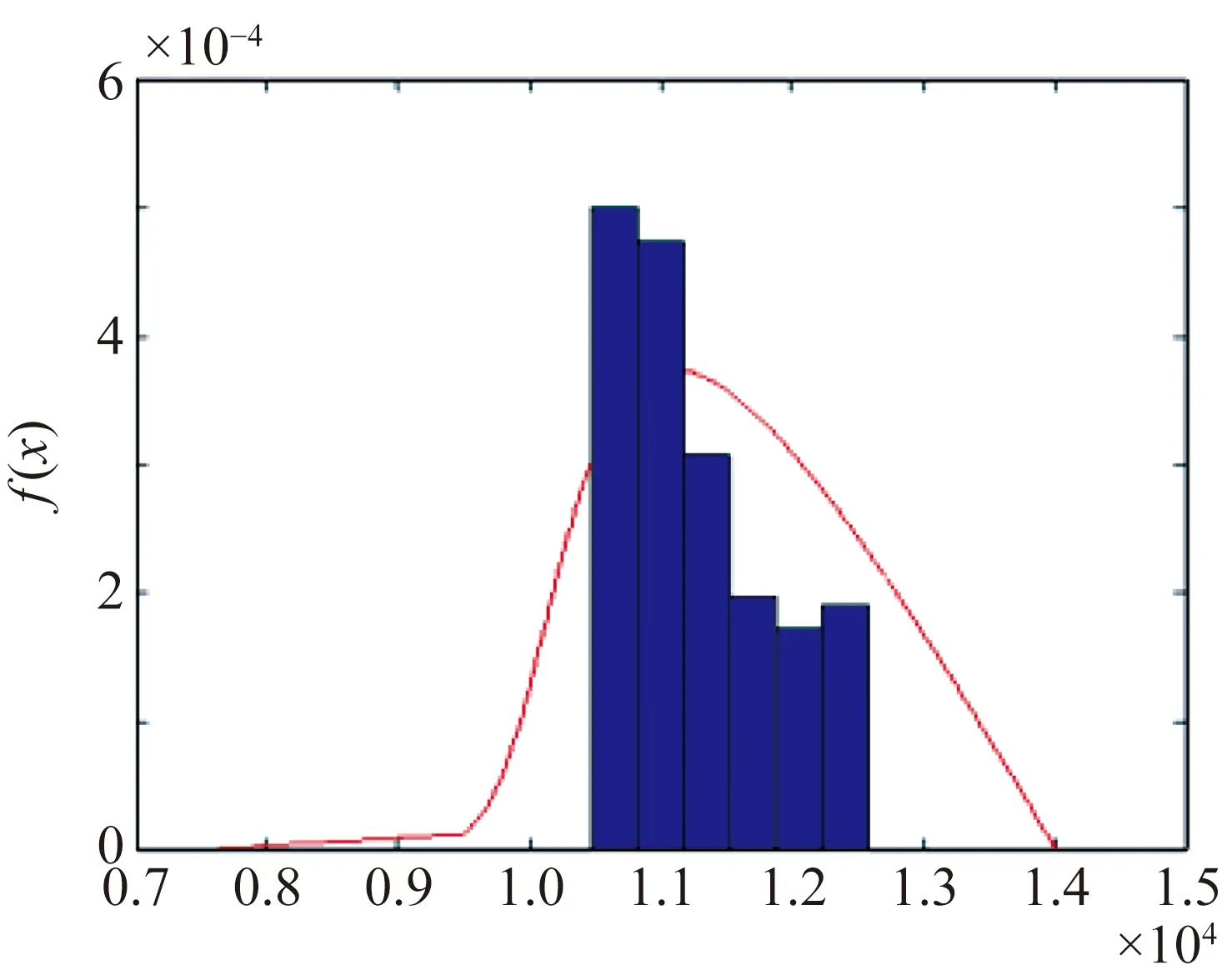
(c)试验序号③(c)Testsequence③

(d)试验序号④(d)Testsequence④

图3光伏组件伪失效寿命λ分布概率密度函数

Fig.3Probability density function of PV moduleλdistribution on pseudo-failure life

为验证光伏组件伪失效寿命分布估算的准确度，课题组在样本组①完成预定1 000 h加速退化试验后继续以原条件进行加速退化，直至达到预定失效条件：输出功率Pd≤80%×P0(P0为初始功率值)，可得该样本组失效寿命和可靠度统计结果，并与本文方法求得结果进行对比，其结果如图4所示。

图4　光伏组件可靠度拟合曲线比对图

可以看出，采用上述方法估算的伪失效寿命分布及其可靠度函数与试验数据统计结果拟合曲线贴合度较好，分析该方法估算结果与试验数据曲线绝对误差、相对误差，除可靠度值边界处外，估算伪失效寿命可靠度与试验数据拟合曲线绝对误差基本在±300 h内，相对误差不超过±15%，满足工程预测精度需求[17]。

4　结　论

本文针对光伏组件产品加速退化条件下可靠度评估，提出一种基于GLD的光伏组件伪失效寿命分布估算方法，利用R2系数优选最佳加速退化轨迹，得到样本组伪失效寿命值；并应用Bootstrap法产生自助样本扩充样本群，改善小子样下分布估算准确性问题；基于广义λ分布构建样本组伪失效寿命分布模型，无需预设先验分布，真实反映不同加速条件下光伏组件伪失效寿命分布形态，最后通过18 W单晶硅光伏组件加速退化应用实例，估算光伏组件加速退化条件下伪失效寿命分布和可靠度。结果表明：在加速退化条件下，利用本文方法得到伪失效寿命分布及其可靠度与试验数据拟合结果贴合度较好，拟合曲线绝对误差基本在±300 h内，相对误差不超过±15%，可满足工程预测精度需求。

[1]晁代宏，马静，陈淑英. 应用多元性能退化量评估光纤陀螺贮存的可靠性[J]. 光学 精密工程， 2011(1):35-39.

CHAO D H， MA J， CHEN SH Y.Assessment of storage reliability for FOGs by multivariate degradati-on data [J].Opt.PrecisionEng.， 2011(1):35-39.(in Chinese)

[2]余荣斌，刘桂雄，徐欢. 基于β分布统示法的光伏组件性能退化可靠度估算[J].仪器仪表学报，2015，11:2586-2593.

YU R B， LIU G X， XU H.β-distribution uniform expression for photovoltaic modules reliability evaluation based on degradation data distribution [J].ChineseJournalofScientificInstrument，2015，11:2586-2593.(in Chinese)

[3]刘桂雄， 何建林， 余荣斌. 光伏组件可靠性评估的研究现状与思考[J]. 现代制造工程， 2014(12):123-126.

LIU G X， HE J L， YU R B.Research status and ponderation of reliability evaluatingmethods on PV modules [J].ModernManufacturingEngineering， 2014(12):123-126.(in Chinese)

[4]CHEN Z H， ZHENG SH R. Lifetime distribution based degradationanalysis [J].IEEETransactionsonReliability， 2005，54(1):3-10.

[5]NELSON W B.AcceleratedTesting:StatisticalModels，TestPlans，andDataAnalysis[M].New York: John Wiley & Sons，2009:493-544.

[6]LU J C， MEEKER W Q. Using degradation measures to estimate a time-to-failure distribution [J].Technimetrics， 1993， 35(2): 161-174.

[7]肖承地， 刘春军， 刘卫东，等.基于加速性能退化的LED 灯具可靠性评估[J].发光学报， 2014(9):1143-1150.

XIAO CH D，LIU CH J， LIU W D，etal.. Reliability assessment of led lamp based on acceleration degradation test [J].ChineseJournalofLuminescence， 2014(9):1143-1150.(in Chinese)

[8]LEE T H， PARK K Y. Degradation analysis of anode-supported intermediate temperature-solid oxide fuel cells under various failure modes [J].JournalofPowerSources， 2015，276(1): 120-132.

[9]邓爱民，陈循，张春华，等. 基于性能退化数据的可靠性评估[J]. 宇航学报，2006(3):546-552.

DENG A M， CHEN X，ZHANG CH H，etal..Reliability assessment based on performancedegrada-tiondata [J].JournalofAstronautics， 2006(3):546-552.(in Chinese)

[10]郭伟玲，樊星，崔德胜，等. 一种基于伪失效寿命的LED 可靠性快速评价方法[J].发光学报， 2013(2):213-217.

GUO W L，FAN X， CUI D SH，etal..Rapid reliability evaluation method of LED based on pseudo-failure lifetime [J].ChineseJournalofLuminescence， 2013(2):213-217.(in Chinese)

[11]柳爱利，寇方勇，寇昆湖. 基于伪寿命分布的退化数据可靠性评估方法[J]. 火力与指挥控制， 2014(8): 102-105.

LIU A L， KOU F Y， KOU K H.Study on Reliability assessment of degradation date based on pseudo life distribution [J].FireControl&CommandControl， 2014(8): 102-105.(in Chinese)

[12]ALLEN F Z， DAVID P D.Photovoltaic moduleweather durability & reliability testing [J].SolarEnergyCompetenceCenter，AtlasMaterialTestingTechnologyLLC，2012.

[13]高攀东，沈雪瑾，陈晓阳，等. 基于自助法的小样本Weibull分布可靠性分析[J]. 机械设计与研究，2015，02:164-167.

GAO P D， SHEN X J， CHEN X Y，etal..Reliability analysis under weibulldistribution in small samples based on bootstrap [J].MachineDesignandResearch， 2015，02:164-167.(in Chinese)

[14]姜焰鸣， 刘桂雄.形状误差粒子群算法智能评定的β分布统示法[J].华南理工大学学报(自然科学版)，2012， 12:30-34+40.

JIANG Y M， LIU G X.β-distribution uniform expression for intelligent form error evaluationbased on particle swarm optimization algorithm [J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition)，2012， 12:30-34+40.(in Chinese)

[15]ZAVEN A， KARIAN.FittingStatisticalDistributions:TheGe-neralizedLambdaDistributionandGeneralizedBootstrapMethods[M]. USA: CRC Press， 2000.

[16]CEI/IEC 61215， Crystalline silicon terrestrialphotovoltaic(PV) modules-Design qualification and type approval [S].Geneva，Switzerland:IEC， 2005.

[17]张慰，李晓阳，姜同敏，等. 基于BP神经网络的多应力加速寿命试验预测方法[J].航空学报，2009(9):1691-1696

ZHANG W， LI X Y， JIANG T M，etal..Life-prediction of multi-stress accelerated life testing based on BP algorithm of artificial neural network [J].ActaaeronauticaETAstronauticaSinica，2009(9):1691-1696.(in Chinese)

导师简介：

刘桂雄(1968-)，男，广东揭阳人，教授，1990年、1995年于重庆大学分别获得学士、博士学位，主要研究方向为测试计量技术及仪器。E-mail：megxliu@scut.edu.cn

余荣斌(1977-)，男，江西景德镇人，博士研究生，高级工程师，1999年、2002年于华南师范大学分别获得学士、硕士学位，主要研究方向为产品可靠性检测。E-mail：robinyu@qq.com

(本栏目编辑：曹金)

(版权所有未经许可不得转载)

Estimation of pseudo-failure lifetime distribution forphotovoltaic modules based on accelerated degradation

LIU Gui-xiong1*， YU Rong-bin1，2， XU Huan1

(1.SchoolofMechanicalandAutomotiveEngineering，SouthChinaUniversityofTechnology，Guangzhou510640，China;2.GuangdongTestingInstituteofProductQualitySupervision，Guangzhou510330，China)*Correspondingauthor，E-mail：megxliu@scut.edu.cn

This paper focuses on the reliability evaluation of photovoltaic(PV) module products under accelerated degradation conditions. A method to estimate the pseudo failure life distribution of PV modules based on the Generalized Lambda Distribution(GLD) was proposed. Firstly， the determinative coefficient test method(R2) was used to select the best accelerated degradation path to obtain pseudo failure life values of samples. Then，the bootstrap method was taken to generate bootstrap samples to expand the sample group and to build a pseudo failure life distribution model based on GLD， which could truly reflect the pseudo failure life distribution of PV modules under different acceleration conditions without presetting the prior distribution， Finally， by taking accelerated performance degradation data of a 18 W small power Mono-Si silicon PV module as an example， the pseudo failure life distribution and reliability of PV modules were estimated under accelerated degradation conditions. The results show that this method obtains pseudo failure life distribution in accelerated degradation conditions， and reliability curves and the experimental data results fit well. Moreover， the absolute error of fitting curve is basically in 300 h， and the relative error is not more than 15%. These results meet the demand of engineering forecast precision.

photovoltaic modulus; accelerated degradation; pseudo-failure lifetime; GLD-distribution；reliability evaluation

2016-02-19；

2016-04-20.

国家质量监督检验检疫总局资助项目(No.2014QK050)；广东省科技厅公益研究与能力建设专项资助项目(No.2014A040401045)

1004-924X(2016)09-2183-09

TM914.4；TB114.3

A

10.3788/OPE.20162409.2183