被测件随机移相干涉面形测量方法
2016-11-10赵维谦李文宇邱丽荣
赵维谦,李文宇,赵 齐,邱丽荣,王 允
(北京理工大学 光电学院,北京100081)
被测件随机移相干涉面形测量方法
赵维谦,李文宇,赵齐,邱丽荣,王允*
(北京理工大学 光电学院,北京100081)
针对光学元件的面形测量,提出了一种被测件随机移相干涉面形测量法,用于降低移相干涉仪的成本,避免移相器老化产生的移相误差对面形检测精度的影响。该方法利用微位移驱动器驱动被测件在摩擦气浮复合导轨上移动进行随机移相并用相机采集若干幅干涉图;然后利用最小二乘迭代算法处理干涉图数据进而迭代出被测表面相位分布;最后进行一系列数据处理求解出被测件的面形结果。为了验证该方法的可行性,在实验室搭建了改进的斐索移相干涉系统,并选用一个凹面镜和一个平面镜作为被测件在搭建的系统上进行了实验测试,同时与同台仪器上的传统移相方法得到的测量结果进行了比对。结果表明:在激光光源波长λ为632.8 nm的情况下,凹球面镜面形PV值和RMS值与传统移相方式测量结果相差0.001λ,和0.002λ;平面镜面形PV值和RMS值与传统移相方式的测量结果相差0.002λ和0.003λ,面形数据基本一致。该方法避免了移相器老化引入移相误差,降低了仪器成本,测量精度高。
干涉测量;面形测量;被测件;移相器;随机移相;最小二乘迭代
1 引 言
在光学元件检测领域,光学元件表面形貌检测占有重要地位,目前主要利用光学干涉测量技术进行表面形貌检测。传统的光学干涉测量方法主要通过直接判读干涉条纹来测量被测面形,精度低、误差大。20世纪80年代,Bruning等人提出移相干涉技术,开启了光学测量领域的新时代[1]。随着激光技术、图像处理技术、光电探测、电子技术与计算机技术在光干涉计量测试领域的应用,移相干涉技术得到了飞速发展。由于具有高精度和高灵敏度等特点,该技术已成为光学元件面形检测领域最有效、最准确的手段之一[2-6]。移相干涉术的基本原理是在干涉仪的参考光和被测光之间引入一定的相移量,这时干涉条纹也会发生相对的移动。通过连续引入相移量,利用相机采集多幅对应相移量的干涉图,最后应用计算机技术按照一定的算法求得面形结果。根据移相干涉技术的基本原理,移相方式主要分为波长移相和移相器移相两大类[7-9]。其中,波长移相是指干涉系统中的激光光源波长可以连续变化,起到移相器的作用,简化了干涉系统的机械结构;移相器移相主要是推动参考镜移相的机械移相方式,可以较为准确地控制移相量,因此其应用更加广泛。目前,世界很多公司具备生产移相干涉仪的能力,其中最著名的便是美国的zygo公司,其生产的移相干涉仪已然成为行业标准。
移相器虽然移相精度较高,但是价格昂贵,并且一旦仪器老化会引入极大的移相误差[10],严重影响面形检测精度。基于此,本文提出了一种被测件随机移相干涉面形测量方法。该方法省去了昂贵的移相器,简化了移相结构,不再是参考镜移相,而是利用微位移驱动器驱动被测件在摩擦式气浮导轨上随机移相;然后利用最小二乘迭代算法迭代出原始相位分布,再经过一系列数据处理进而求解出被测件的面形结果[11-13]。为了验证该方法的可行性,改造了实验室搭建的斐索移相干涉系统,增加了微位移驱动器及控制器,编写了最小二乘迭代算法,并与同台仪器上五步移相法的测量结果进行比对,两个测量结果一致,从而证明方法可行。
2 被测件随机移相干涉系统及算法
2.1系统原理
本文以测量凹球面面形为例,构建了如图1所示的被测件随机移相干涉面形测量系统,该系统基于已有的斐索移相干涉仪,在硬件方面增加了驱动控制模块,在软件方面增加了最小二乘迭代算法模块。被测件随机移相干涉测量系统的光路走向为:准直透镜将点光源出射的光准直成平行光后照射在参考物镜上,由参考物镜会聚成测量光束照射在被测透镜表面。参考物镜的最后一个表面为参考面,参考镜处的箭头表示一路光在参考镜处原路返回,被测镜处的箭头表示透射光在被测镜面处原路返回。由参考面反射回来的光束和由被测球面表面反射回来的光束沿原光路返回后形成干涉条纹。本文通过微位移驱动模块推动被测件在导轨上移相来改变参考波面和被测波面之间的相对相位差。在移相过程中,相机采集若干(大于等于3幅)幅干涉条纹图,然后通过最小二乘迭代算法处理干涉条纹图像得到波前相位分布,因为涉及到反正切函数,相位被包裹在[-π,π],因此还需要对迭代出的相位分布进行解包裹和波面拟合等[14-17]。

图1 被测件随机移相干涉系统原理
Fig.1Principle of measured element randomly phase shifting interferometry system
2.2最小二乘迭代算法
由于本系统采用随机移相方式,传统的移相算法不再适用,所以本文利用最小二乘迭代算法来重构原始相位分布。
2.2.1根据已知的移相量求解相位分布
根据经典的双光束干涉理论,空间某点(x,y) 干涉场的光强分布为:
aj+bjcosδi+cjsinδi.
(1)
式中:i=1,2,…,N(N≥3)表示采集干涉图的帧序号,j=1,2…,M表示一帧干涉图里像素的序号,t表示理论光强。并且式(1)中有:
aj=Ai,j,
bj=Bi,jcosφj,
cj=-Bi,jsinφj,
(2)
其中:Ai,j是该像素光强的直流分量,也称为背景光;Bi,j是该像素的调制度;φj是该像素对应的被测相位;δi是第i帧干涉图对应的移相值。假定对于任意一个像素点,各帧干涉图在此像素的背景光强和调制度是一致的,由最小二乘法原理,理论光强与实际光强的最小值为:

(3)
根据最小二乘法则,若要使min取得最小值,式(3)代入移相值后求导得零,可以求解出干涉图中每一点的bj和cj,进而推导出N步移相法求解波面相位的一般式:

(4)
2.2.2根据已知的相位分布求解移相量
利用式(4)得到的相位分布,可以从相反的过程来求解各帧干涉图对应的移相量。依然假定对于任意一个像素点,各帧干涉图在此像素的背景光强和调制度是一致的,不发生变化。由双光束干涉理论有:
ai+bicosφj+cisinφj,
(5)
式中:
ai=Ai,j,
bi=Bi,jcosδi,
ci=-Bi,jsinδi.
(6)
和式(1)类似,得出第i帧干涉图中各点的理论光强与实际光强的最小二乘差值:
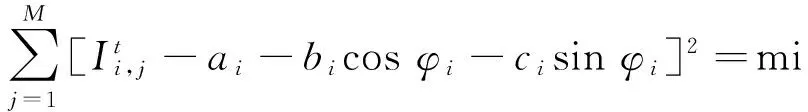
(7)
根据最小二乘法则,对式(7)求导使其得零并代入相位值,计算可求得bi和ci,进而得到第i帧干涉图对应的移相值为:

(8)
2.2.3开始迭代并设定收敛条件
首先设定一个初始移相值,代入式(1)求得相位分布;然后将式(1)中求得的相位代入式(2)中可以求得各帧干涉图对应的移相值;最后判断迭代是否满足收敛条件。如果不满足,则将本次迭代得到的移相值继续代入式(1)中,进行下一次迭代,直到满足条件为止。其中,收敛条件用来判断各帧干涉图间的移相值是否达到了精度要求,表达式为:
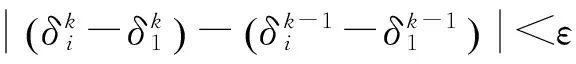
(9)
式中:k是迭代次数,ε是收敛阈值。按照上面的迭代可以精确求解出原始相位分布和移相量。
用上述迭代求解方法,可以求得精准的相位分布,但由于相位求解时涉及到反正切函数,所以求得的相位包裹在-π~π,因此还需要进行包裹相位解包裹和波面拟合等步骤,即可得到面形结果。
2.3系统装置
如图2所示,本系统主要包括干涉测量主机、装载被测件的五维调整架、摩擦气浮复合导轨、导轨移相驱动系统以及参考镜和被测件。测量时激光波长λ=632.8 nm。图2中的被测件随机移相主要涉及两个关键部分。第一部分是在斐索移相干涉系统的基础上增加了图2右边的移相驱动模块,该移相驱动模块主要包括压电陶瓷微位移驱动器和控制器,驱动器运行平稳,产生的机械振动很小,满足移相使用要求,并且其运行过程中可以产生22 N的推力,满足移相驱动需求。如图2所示,压电陶瓷微位移驱动器顶在气浮导套的中间。移相时,微位移驱动器推动导套移动,进而完成被测件移相。由于总移动量控制在一个波长以内,因此在球面面形测量时产生的离焦对面形的影响极小,可忽略不计[18]。第二部分是摩擦气浮复合导轨部分,摩擦气浮复合导轨的精度非常高,保证了移相的直线度和稳定性。

图2 被测件随机移相干涉系统
Fig.2Photo of measured element randomly phase shifting interferometry system
3 实验验证
为了验证该方法的可行性,分别选取了凹球面镜被测件和平面镜被测件在同台仪器上用被测镜随机移相方法和传统五步移相法进行测量比对实验,实验平台为光学隔振平台。
3.1凹球面镜面形测量结果
在图2所示的测量系统中,使用zygo标准物镜作为系统参考物镜,焦距f=150 mm,表面面形精度可达λ/20。图3的凹球面镜是实验被测件, 其曲率半径r=25 mm。
实验时,控制驱动器推动被测件移相,同时相机采集若干幅干涉图。接着将采集到的干涉图代入最小二乘迭代算法中,迭代出包裹相位分布。然后进行解包裹和波面拟合等数据处理,最后求得被测件的面形结果。这里的面形测量结果都是相对于参考面的想对面形。

图3 凹球面镜
图4是实验测量结果,从测量结果可以看出,两种移相方法测得的面形结果PV值仅相差0.001λ,RMS值仅相差0.002λ,面形结果非常接近,证明方法可行。

(a)随机移相

(b)传统五步移相
3.2平面镜面形测量结果
在图2所示的测量系统中,使用zygo公司提供的标准平面镜作为系统参考镜,其表面面形精度可达λ/20,图5的平面镜是实验被测件。

图5 平面镜

(a)随机移相

(b)传统五步移相
图6为平面镜面形测量结果,由结果可以看出,两种移相方法测得的面形结果PV值仅相差0.002λ,RMS值仅相差0.003λ,面形结果基本一致,证明方法可行。
对比上述两个不同被测件的实验结果可知,本文的被测件随机移相测量方法的面形结果与同台仪器上的五步移相法的测量结果基本一致,由此验证了本方法的可行性。
4 结 论
本文提出了一种被测件随机移相干涉面形测量方法,省去了移相器,避免了移相器老化带来的移相误差并且降低了成本。利用微位移驱动器推动气浮导套在摩擦气浮复合导轨上进行移动,完成被测件移相并采集若干幅干涉图,然后通过最小二乘迭代算法迭代出被测表面的包裹相位分布,再经过一系列数据处理解算出面形结果。为了验证该方法的可行性,在同一仪器上与传统五步移相方法进行比对,实验结果表明:对于凹球面镜,该方法与同台仪器的五步移相方法相比,PV值仅相差0.001λ,RMS值仅相差0.002λ;对于平面镜,该方法与同台仪器的五步移相方法相比,PV值仅相差0.002λ,RMS值仅相差0.003λ,由此证明了方法的可行性。不过,本文方法仍有待进一步的研究,比如导轨在移相过程中的影响分析、误差分析等。
[1]BRUNING J H, HERRIOTT D R, GALLAGHER J E,etal.. Digital wavefront measuring interferometer for testing optical surfaces and lenses [J].AppliedOptics, 1974, 13(11): 2693-2703.
[2]朱日宏,陈磊,王青,等. 移相干涉测量术及其应用[J]. 应用光学, 2006,27(2):85-88.ZHU R H, CHEN L, WANG Q,etal.. Phase-shift interferometry and its application[J].JournalofAppliedOptics, 2006,27(2):85-88. (in Chinese)
[3]黄根旺. 斐索型移相式激光干涉仪研究[D]. 哈尔滨:哈尔滨工业大学, 2011.
HUANG G W.ResearchonFizeauPhase-shiftingLaserInterferometer[D]. Harbin:Harbin Institute of Technology,2011. (in Chinese)
[4]于瀛洁,韦春龙,陈明仪. 移相式数字波面干涉仪中的几个技术问题[J]. 光学 精密工程, 2001,9(6): 584-587
YU Y J, WEI CH L, CHEN M Y. Technical problems in digital phase-stepping flatness interferometers[J].Opt.PrecisionEng., 2001,9(6): 584-587. (in Chinese)
[5]任寰,马力,刘旭,等. 多表面干涉情况下光学元件面形检测技术[J]. 光学 精密工程, 2013,21(5): 1144-1150.REN H, MA L, LIU X,etal.. Optical element test with multiple surface interference[J].Opt.PrecisionEng., 2013,21(5): 1144-1150. (in Chinese)
[6]曹华梁,程祖海,余亮英. 用干涉条纹图像重建反射镜的三维面形[J]. 光学 精密工程,2007,15(4):599-603.
CAO H L, CHEN Z H, YU L Y.Reconstruction of 3-D surface of mirror by processing fringe pattern[J].Opt.PrecisionEng., 2007,15(4):599-603. (in Chinese)
[7]于瀛洁,张本好,焦云芳. 波长移相干涉仪的算法研究[J]. 光学 精密工程, 2003,11(6): 560-566.
YU L J, ZHANG B H, JIAO Y F. Algorithms of the phase-shifting interferometer via wavelength tuning[J].Opt.PrecisionEng., 2003,11(6): 560-566. (in Chinese)
[8]吴栋,朱日宏,陈磊,等. 抗振型移相干涉仪中PZT移相器的改进[J]. 光学 精密工程, 2003,11(6): 567-571.
WU D, ZHU R H, CHEN L,etal..Improvement of PZT phase shifter in vibration-resistant phase-shifting interferometer[J].Opt.PrecisionEng., 2003,11(6): 567-571. (in Chinese)
[9]刘江,苗二龙,曲艺,等. 基于光强自标定移相算法检测光学面形[J]. 光学 精密工程, 2014,22(8): 2007-2013.
LIU J, MIAO E L, QU Y,etal.. Measurement of optical surface based on intensity self-calibration phase-shift algorithm[J].Opt.PrecisionEng., 2014,22(8): 2007-2013. (in Chinese)
[10]赵智亮,夏伯才,陈立华,等. 相移干涉测量中相移误差的自修正[J]. 光学 精密工程, 2013,21(5): 1116-1121.
ZHAO ZH L, XIA B C, CHEN L H,etal.. Self-correction of phase step error in phase shifting interferometry measurement[J].Opt.PrecisionEng., 2013,21(5): 1116-1121. (in Chinese)
[11]武迎春, 曹益平, 肖焱山. 任意相移最小二乘法迭代的在线三维检测[J]. 光学 精密工程, 2014,22(5): 1347-1353.WU Y CH, CAO Y P, XIAO Y SH.On-line three-dimensional inspection using randomly phase-shifting fringe based on least-square iteration [J].Opt.PrecisionEng., 2014,22(5): 1347-1353. (in Chinese)
[12]苏志德,史振广,苏东奇,等. 在随机和倾斜移相下光强归一化的迭代移相算法[J].光学学报, 2013,33(1): 0112001-1-7.SU ZH D, SHI ZH G, SU D Q,etal.. Iterative phase shifting algorithm with normalized intensity in the presence of random and tilt phase shifts [J].ActaOpticaSinica, 2013,33(1): 0112001-1-7. (in Chinese)
[13]苏志德,隋永新,杨怀江,等. 迭代最小二乘法用于非线性移相器的标定[J].应用光学, 2013,33(1): 0112001-1-7.
SU ZH D, SUI Y X, YANG H J,etal.. Calibration of nonlinear phase shifter with iterative least-square method [J].JournalofApplicedOptics, 2013,33(1): 0112001-1-7. (in Chinese)
[14]郭媛, 陈小天. 基于最小二乘相位解包裹改进算法的研究[J]. 中国激光, 2014, 41(5): 195-200.
GUO Y, CHEN X T. Study of improved phase unwrapping algorithm based on least squares [J].ChinaJournalofLasers, 2014, 41(5): 195-200. (in Chinese)
[15]李国栋,韦春龙,于瀛洁,等. 圆形域干涉图中的相位解包裹[J]. 光学 精密工程, 2000,8(5): 473-477.LI G D, WEI CH L, YU Y J,etal.. Phase-unwrapping for interferograms with circle field [J].Opt.PrecisionEng., 2000,8(5): 473-477. (in Chinese)
[16]单宝忠,王淑岩,牛憨笨,等. Zernike多项式拟合方法及应用[J]. 光学 精密工程, 2002, 10(3): 318-323.
SHAN B ZH, WANG SH Y, NIU H B,etal.. Zernike polynomial fitting method and its application [J].Opt.PrecisionEng., 2002, 10(3): 318-323.(in Chinese)
[17]WANG J Y, SILVA D E. Wave-front interpretation with Zernike polynomials [J].AppliedOptics, 1980, 19(9): 1510-1518.
[18]杨佳苗.激光差动共焦干涉元件参数测量方法与技术研究[D]. 北京:北京理工大学,2015.
YANG J M.LaserDifferentialConfocalandInterferenceMeasurementMethodandTechnologyforElementParameters[D]. Beijing:Beijing University of Technology,2015.(in Chinese)

王允(1984-),男,山东威海人,博士,讲师,硕士生导师,2013年于北京理工大学获得博士学位,主要从事精密光电测试技术与仪器装备方面的原理方法、关键技术以及仪器装备系统集成技术的研究及应用。E-mail:alotrabbits @163.com
(版权所有未经许可不得转载)
Surface measurement by randomly phase shifting interferometry of measured element
ZHAO Wei-qian, LI Wen-yu, ZHAO Qi, QIU Li-rong, WANG Yun*
(SchoolofOptoelectronics,BeijingInstituteofTechnology,Beijing100081,China)*Correspondingauthor,E-mail:alotrabbits@163.com
For the surface measurement of optical elements, a surface measurement method by the randomly phase shifting interferometry of measured element was proposed to reduce the cost of phase shifting interferometer and to avoid phase-shifting error caused by an aged phase shifter. A micro-displacement driver was used to drive a measured element to move on a friction type air-bearing slider to implement the random phase shift, meanwhile, several interfere grams were collected by a camera. Then, the interferograms were processed by least-square iteration algorithm and the phase distribution of the measured element surface was iterated. Finally, the surface measurement result was calculated by a series of data processing and the surfaces of measured elements were obtained. To verify the feasibility of the proposed method, a Fazi phase shift interferometer was improved and a concave spherical mirror and a plane mirror were used as measured elements to perform the comparative experiment between the article’s method with the traditional phase shifting method on the same instrument. Experimental results indicate that when the laser wavelengthλis 632.8 nm, the PV difference and the RMS difference between the two results are only 0.001λand 0.002λ, respectively for the concave spherical mirror. Moreover, those between the two results are only 0.002λ, and 0.03λ,respectively for the plane mirror. These surface data are basically consistent. Experimental results show that the measurement method avoids the phase-shifting error caused by the aged phase shifter, and it has high accuracy and low cost.
interferometry; surface measurement; measured element; phase shifter; randomly phase shifting; least-square iteration
2016-05-05;
2016-06-14.
国家重大科学仪器设备开发专项资助项目(No.61327010);国家自然科学基金青年基金资助项目(No.51405020)
1004-924X(2016)09-2167-06
TH741.3
A
10.3788/OPE.20162409.2167

赵维谦(1966-),男,新疆伊宁人,教授,博士生导师,1993年,2003年于哈尔滨工业大学分别获得硕士、博士学位,主要从事光学测量领域的研究。E-mail:zwq669@126.com
