涡轮转子叶片-轮盘的振动特性分析

杨修伟,黄 磊

(大连理工大学机械工程学院，辽宁 大连 116023)



涡轮转子叶片-轮盘的振动特性分析

杨修伟,黄 磊

(大连理工大学机械工程学院，辽宁 大连 116023)

针对航空发动机涡轮转子叶片-轮盘常出现故障的问题，分别对单个叶片和耦合叶片-轮盘(叶盘)在不同边界条件下进行振动特性分析，为叶片-轮盘的设计优化和振动安全性检验提供数值依据，并通过对比分析得出相关结论。

航空发动机；涡轮转子；叶片-轮盘；振动分析

1 引 言

涡轮转子叶盘是航空燃气涡轮发动机的重要组件，工作时受较高的振动交变、离心负荷等作用，容易产生故障。据相关统计，振动故障率占涡轮发动机总故障率的60%左右，而叶片振动故障又占振动故障率的70%以上。

关于叶盘的振动特性分析，国内外较多的是把叶片和轮盘作为孤立元件分别进行研究，如王文亮[1]等利用串接式加载技术分析了固定支撑机构的带冠叶片；张锦[2]在对带冠叶片分析时，利用了群论算法和链式加载技术相结合的方法，这种分析方法忽略了叶片与轮盘的耦合作用，不能反映叶片真实振动特性。在叶盘耦合的振动分析方面，有许多学者做了工作，如HADER[3]将厚壳扭曲的叶片简化为周向与径向的梁模型以估算叶盘离心力的刚度效应；刘廷毅[4]采用群论算法分析叶盘耦合动力特性的回转对称性。为避免叶盘振动故障的出现，有必要在叶片和轮盘的设计过程中应用有限元分析软件进行振动固有特性分析，分析振型、固有频率、振动应力分布[5-6]。

本文首先建立了某型号发动机涡轮叶片及其涡轮叶盘的三维立体模型，而后对模型进行相应简化，然后导入到ANSYS中，对其进行有限元模态分析，计算得出固有频率及其对应振型，结合振型特点，对其进行了分析，为以后叶片及叶盘的设计优化以及振动安全性检验提供了重要的数值依据。

2 三维模型的建立

2.1单个叶片建模

该叶片原型为某型航空发动机第一级涡轮叶片，叶身为扭转型曲面，按照实际部件进行相应的简化，利用三维设计软件建立了叶片的实体三维模型，如图1所示。

图1 单个叶片模型

2.2 涡轮叶盘结构建模

在涡轮叶盘的建模过程中，按照相似性的原则，按照一定比例缩小绘制模型。在不影响有限元分析结果的前提下，对轮盘的盘缘倒角、叶冠之间的间隙以及叶片榫头的大小等均进行简化。为了减小涡轮轮盘的厚度对涡轮叶盘结构影响，特采用涡轮叶盘整体建模的方式，这样既能减轻计算量，又保证了分析结果的准确性，参照文献[7]中叶片工作的属性，叶片属性如表1所示。

表1 叶片属性

本文所分析的涡轮叶盘主要分为两种，一种为带冠涡轮叶盘，另一种为不带冠涡轮叶盘，三维模型如图2所示。

图2 涡轮叶盘无冠(左)有冠(右)

3 有限元计算及分析

3.1 单个叶片计算分析

本文在单个叶片的计算分析中，根据部件的实际工作情况，分别考虑两种边界条件：简单边界条件，在第一道榫齿工作面(即叶片与轮毂的接触工作面)加载全约束；复杂边界条件，在第一道榫齿工作面加载全约束及叶冠位置周向两侧工作面加载周向位移协调(即法向位移约束)。对单个叶片进行网格划分，最小的边界尺寸为0.361180mm，节点数为42741，单元数为24518。首先，对叶片加载简单约束并计算其固有频率，结果如表2所示，部分位移振动云图如图3所示。

表2 简单边界条件下叶片的各阶频率(Hz)

图3 简单边界条件第五阶位移振动云图

对单个叶片模型加载复杂边界条件，计算其固有频率，其结果如表3所示，部分位移振动云图如图4所示。

表3 复杂边界条件下叶片前五阶频率(Hz)

图4 复杂边界条件第五阶位移振动云图

对比两种边界条件下的固有频率，结果如表4所示。

表4 简单与复杂边界条件下固有频率的对比

可以知道，随着阶次的增加，两种边界条件的相对频差逐步降低，即叶冠对单个叶片固有频率的影响降低；在复杂边界条件下加载的叶冠周向两侧工作面的法向约束，明显提高了叶片的固有频率，降低了因低阶激励而引起叶片共振的可能，故而复杂边界下叶片的固有频率要比简单条件大得多。对比图3和图4，简单条件下叶片振型的位移变形主要集中在叶身的中上部且变形较大，而复杂条件时，叶片振型的位移变形主要集中在叶身的中部且变形较小，而且由于叶根第一道榫齿工作面上加载了全约束，因此存在应力集中。

3.2 涡轮叶盘结构计算分析

主要对涡轮叶盘结构有限元简化模型进行模态计算分析，以带冠叶盘模型为例，计算叶盘的各阶固有频率。叶盘结构的网格划分情况如下：带冠叶盘单元数为49014，节点数为90266。计算带冠涡轮叶盘结构在不同边界条件的固有频率，其结果如表5所示。在相同的边界条件时，无冠涡轮叶盘固有频率与有冠涡轮叶盘固有频率的对比如表6所示。

表5 带冠叶盘在不同边界条件的各阶频率

表6 无冠叶盘与有冠叶盘在限制内轮毂条件时各阶频率

阶次有冠固有频率(Hz)无冠固有频率(Hz)相对频率(%)15116.26010.717.4825140.96053.517.7535142.06055.417.7645315.56285.418.2555316.26286.618.26

图5 带冠叶盘在限制内圈时第五阶云图

图6 带冠叶盘在限制内轮毂时第五阶云图

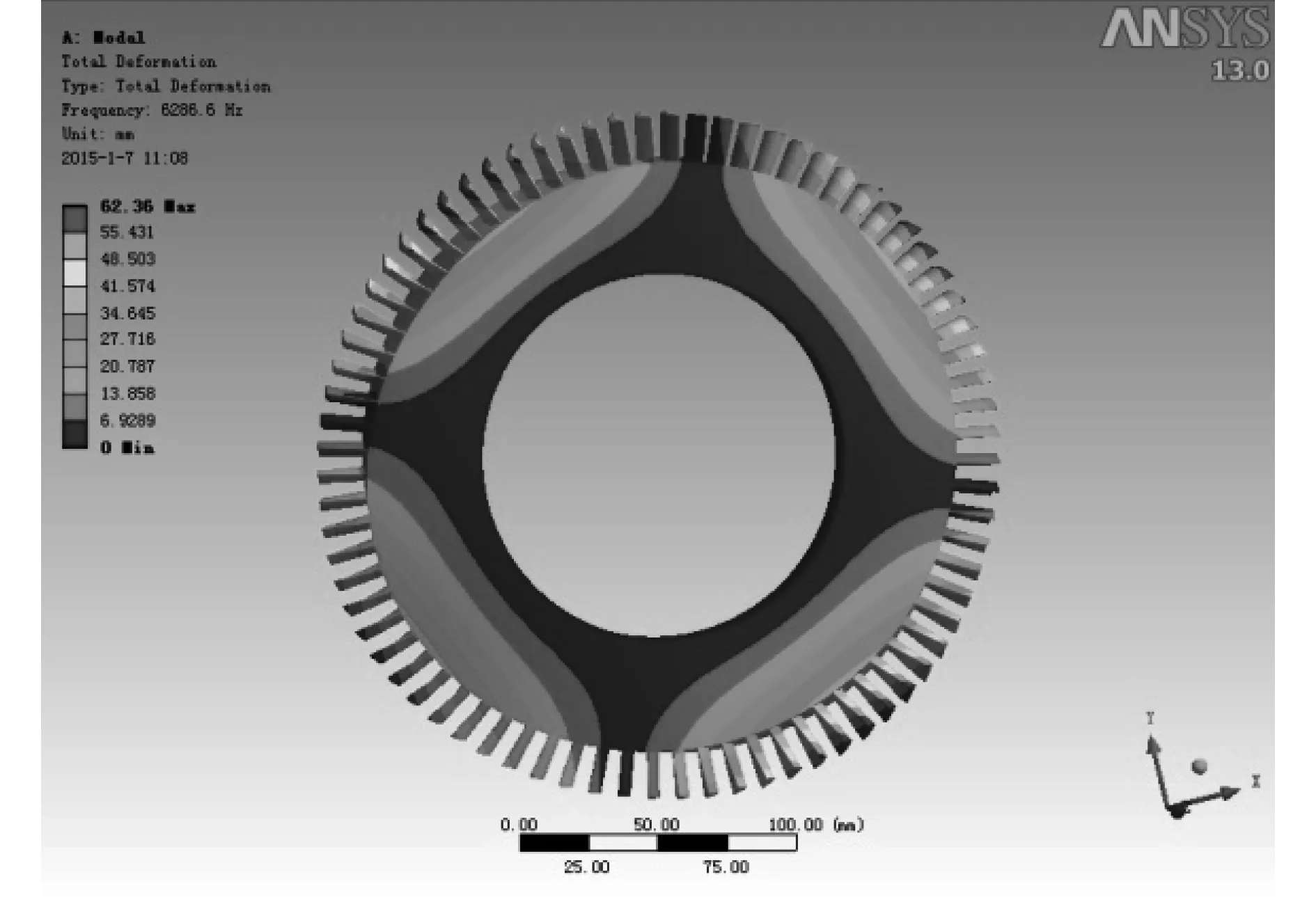
图7 无冠叶盘限制内轮毂时第五阶云图

如图5与图6所示，分析的涡轮叶盘结构的位移云图呈现出伞状、扇形发散状以及复合振动的情况。从图6所示的位移振动云图可以看出，涡轮叶盘存在正交的模态，这也体现了典型盘类结构模型的共有特征。如图6和图7所示，无冠叶盘与带冠叶盘在相同的边界条件下，无冠叶盘位移振动幅度要远大于带冠叶盘，这说明带冠叶盘显著增强了叶盘结构的刚性，使得叶盘振动位移情况明显减弱。此外，无冠叶盘的各阶振型特点在带冠叶盘的振型中都有体现。

根据表5的结果，可以看出，涡轮叶盘在限制内圈的边界条件时，与限制内轮毂边界条件相比，轮盘的整体频率有较大提高。这主要是由于叶盘被限制内圈时，导致涡轮叶盘的整体刚性提升。同时， 涡轮叶盘限制内圈与限制内轮毂的各阶相对频率逐步增大，且叶盘在限制内轮毂时，各阶频率变化不大，这表明单纯地限制轮盘内轮毂对于提高轮盘整体刚性作用不大。

根据表6的结果，可以看出，在相同的边界条件时，无冠涡轮叶盘结构的固有频率要高于有冠叶盘，这也验证了实际情况中叶盘结构的固有频率受几何尺寸、材料属性、载荷等因素的影响，相同的边界条件下，有冠叶盘固有频率不一定比无冠叶盘频率高。

4 结 论

本文分析了某航空发动机高压涡轮转子单个叶片固有频率、在复杂边界条件下的动频及振型和相对应力分布特性，计算了涡轮叶盘有冠和无冠结构在不同边界条件下的固有频率以及各阶振型，得出如下结论：

(1)叶片在复杂边界条件时，各阶的固有频率与简单条件下相比有显著的提高。由于复杂边界条件下增加了叶片周向工作面的法向位移约束，增加了叶片整体的结构刚性，使得叶片的固有频率大大提高，有效降低了因低阶次激振力而引起叶片共振的可能。

(2)通过对无冠和有冠的涡轮叶盘分析可以得出，叶冠增加了叶盘的整体刚性，使得在相同的边界条件下，有冠叶盘的位移应变更小。此外，涡轮叶盘在限制内圈时，涡轮叶盘的整体刚性提升较大，而单纯地限制轮盘内轮毂对于提高轮盘整体刚性影响不大。此外，由于受几何尺寸、材料属性等影响，相同的边界条件下，有冠叶盘固有频率不一定比无冠叶盘频率高。

[1]王文亮,陈向均,李祚长,等.串接式BENFIELD对接加载约束子结构法-带冠涡轮叶片和压气机叶片的动力分析[J].宇航学报,1984,(4):12-14.

[2]张锦.环向圈连带冠叶片的动态分析[J].航空学报,1991,(9):474-481.

[3]HADER N.Shaft flexibility effects on the forced response of a bladed-disk assembly[J]. Mechanical Engineering Department,1988,(6):102-109.

[4]刘廷毅.叶片-轮盘-轴系统的耦合振动分析[J].燃气涡轮试验与研究,1996,(1):30-34.

[5]伍登峰,张松林.某型发动机高压涡轮盘-叶耦合共振特性分析[J].航空发动机,2004,30(1):55-58．

[6]孟庆迪,罗贵火.某型发动机涡轮盘整体振动模态的有限元分析[J].振动工程学报,2004,17(5):113-115．

[7]罗泽明,郑丽,丁伟.基于ANSYS的某型航空发动机涡轮叶片的振动特性分析[J].现代机械,2014,(02):36-39.

Vibration Characteristic Analysis of Turbine Rotor Blade-Wheel

Yang Xiuwei, Huang Lei

(School of Mechanical Engineering, Dalian University of Technology, Dalian 116023, Liaoning, China)

In order to solve the failures of turbine rotor blade-wheel of aero-engine, the vibration characteristics of singer blade and blade-wheel under different boundary conditions are analyzed to provide a numerical basis for vibration safety inspection and design optimization of blade-wheel. Lastly, the relevant conclusions are drawn through the comparative analysis.

aero-engine; turbine rotor; blade-wheel; vibration analysis

2016-06-16

杨修伟，男，山东省沂南县人，大连理工大学硕士研究生，研究方向：机电一体化，机械设计及理论。

V232.4

B

10.3969/j.issn.1674-3407.2016.03.004