Adaptive Dynamic Feedback Tracking Control for a Robot-camera System with Unknown Parameters

LIANG Zhen-Ying　WANG Chao-Li　CHEN Hua　LI Cai-Hong

Adaptive Dynamic Feedback Tracking Control for a Robot-camera System with Unknown Parameters

LIANG Zhen-Ying1WANG Chao-Li2CHEN Hua3LI Cai-Hong4

The tracking problem of nonholonomic mobile robots with uncertainties is investigated in this paper.An uncertain model of the nonholonomic kinematic system is presented based on the visual feedback and the state and input transformations for a kind of mobile robots in chained form with uncertainties.Two transformations are exploited based on the idea of backstepping and the structure of tracking error system.Then，both an adaptive control law and a dynamic feedback robust controller are designed to track the desired trajectory by using Lyapunov direct method and the extended Barbalat Lemma.The asymptotic convergence of a closed-loop error system is proved rigorously.Finally，simulation results demonstrate the effectiveness of the proposed strategies.

Adaptive control，chained system，feedback，mobile robot，tracking control

The tracking control is a complicated problem due to coupled and nonlinear system dynamics［12-16］.In［12］，adaptive force tracking controllers were proposed which not only ensure the entire state of the system to asymptotically converge to the desired trajectory but also ensure the constraint force to asymptotically converge to the desired force. In［13］，Wang et al.proposed a robust adaptive tracking controller which not only can guarantee robustness to parametric and dynamics uncertainties but also can reject any bounded，immeasurable disturbances entering the system. Based on Lyapunov′s direct method and backstepping technique in［6］and［15］，the time-varying global adaptive controllers were presented which simultaneously solved bothtracking and stabilization for mobile robots with unknown kinematic and dynamic parameters.

Visual feedback is an important approach to improve the control performance for robots and manipulators since it mimics the human sense of vision and allows for operating on the basis of noncontact measurement and unstructured environment.Since the late 1980s，tremendous effort has been made to visual servoing［16-21］and vision-based manipulations.In order to develop an adaptive tracking controller for a mobile robot that compensated for the parametric uncertainty in the camera and the mobile robot dynamics，the feedback from an uncalibrated，fixed（ceilingmounted）camera was used in［16］.In［18］，a visual servo tracking controller was developed for a monocular camera system mounted on an underactuated WMR subject to nonholonomic motion constraints.In［19］，a new controller for controlling a number of feature points on a robot manipulator was presented to track desired trajectories specified on the image plane of a fixed camera.Recently，［20］presented a dynamic feedback tracking controller for the nonholonomic WMR of unicycle type with unknown camera parameters.In［11］，a series of new chained models of nonholonomic mobile robots with uncalibrated visual parameters were shown.In［21］，the trajectory tracking control problem of another kind of uncertain dynamic nonholonomic mobile robot（called type（1，1）robot）was addressed where a new adaptive torque tracking controller was presented for tracking error model. For type（1，2）robot，which has two steering wheels and one castor wheel with unknown visual parameters，a new and simple robust stabilization controller［11，22］was designed for a particular case. However，the corresponding tracking problem has not been discussed.Comparing with［16］，in this paper，we design an adaptive dynamic feedback controller to compensate for the unknown camera parameter.Based on Lyapunov direct method and the idea of back-stepping technique，two transformations are chosen.The controllers can make the mobile robot tracking the desired trajectory in the image space and work-space.

The paper is organized as follows.Section 1 addresses robot-camera system configuration.In Section 2，an uncertain chained form model is presented，and the tracking problems are proposed.Section 3 addresses the designs of adaptive and dynamic feedback tracking controllers forthe uncertain kinematic error system and gives the rigorous proof of the asymptotical convergence of the closed-loop error system.Then，the tracking problems in work-space of the mobile robot are presented.In Section 4，simulation results are provided to illustrate the effectiveness of the proposed control strategy.Finally，the major contributions of the paper are summarized in Section 5.

1　Robot-camera system

In this section，we will address robot-camera system configuration.

In Fig.1，a robot-camera system is shown.It is assumed that a pinhole camera is fixed to the ceiling，the type（1，2）mobile robot is under the camera.The movement of the mobile robot can be measured by using a fixed camera.It is assumed that the camera plane runs parallel to the mobile robot plane，and the camera can capture images throughout the entire robot workspace.In the robot-camera system，three coordinate frames exist，namely the inertial frame X-Y-Z，the camera frame i-j-k and the image frame i1-o1-j1.Assume that the i-j plane of the camera frame is parallel to the plane of the image coordinate plane.The direction of corresponding coordinate axis is identical.But the coordinate of the original point of the camera frame with respect to the image frame is defined by（Oc1，Oc2）. C（cx，cy）is the crossing point between the optical axis of the camera and X-Y plane.

Fig.1　Wheeled mobile robots with monocular camera

1.1Robot kinematic system

In Fig.1，the type（1，2）mobile robot［7］is in the X-Y plane which has two steering wheels（conventional centered orientable wheels）and one castor wheel（conventional offcentered orientable wheel）.P is the mid-distance point between the centers of these two steering wheels，with i2aligned along the line joining their centers.A and B are the center points of two steering wheels respectively.L is the distance between point P and point A（or point P and point B）.It is also the distance between point P and the joint point of the castor wheel.θ denotes the angle between i2axis and X axis，β1and β2denote the angles between the orientation of the plane of steering wheels and i2axis respectively.Assume that the geometric center point and the mass center point of the robot are the same.The nonholonomic constraints are described［7］by

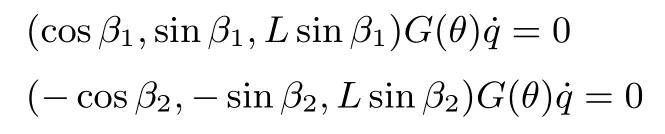
where q=（x，y，θ）T，and

Then the nonholonomic kinematic system［7］can be given by

where v1is the velocity of the robot，v2and v3are the angular velocities of two steering wheels respectively.

For system（1），if sin（β2-β1）=0，then β1=β2=0 or β2=β1+kπ（k=±1，±2，···）.Consider the two nonholonomic constraints along the wheel plane given by［7］.One obtains that the type（1，2）mobile robot is stopped（i.e.，v1=0）or this robot is vestigial to type（2，0）robot. The tracking and stabilization problems are discussed in many papers such as［20-21］.

For system（1），if sin（β2-β1）/=0，choose the state-input transformation［3］as

We obtain the following chained system

System（3）is called canonical chained form system［8］.Generally，（x，y）in（1）needs to be measured for feedback.The encoders can be used to do it.However，over-shoot and low precision are their main drawbacks.Camera is a convenient sensor to implement non-contact and unstructured measurement.The data from a camera can be used for the robot tracking problem.

1.2Camera system model

In Fig.1，the coordinate of the mass center P is（x，y）for the robot with respect to X-Y plane.Suppose that Pm（xm，ym）is the coordinate of（x，y）relative to the image frame.Pinhole camera model yields

where α1and α2are positive constants and dependent on the depth information，focal length，scale factors［16］defined as follows

where z∈R1represents the constant height of the camera optical center with respect to the task-space plane，f∈R1is a constant representing the camera′s focal length，the positive constants denoted by ρ1，ρ2∈R1，represent the cameras constant scale factors（in pixels/m）along their respective Cartesian directions，respectively［16］.And

where θ0denotes the angle between j axis and X axis which represents the constant，anticlockwise rotation angle of the camera coordinate system with respect to the task-space coordinate system.

Therefore，the kinematic system in the image frame can be rewritten as

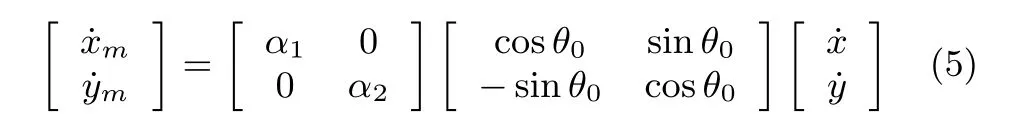
In this paper，it is assumed that（x，y）in（1）is measured by using a camera with uncalibrated visual parameters shown in Fig.1.The pose of the mobile robot in the workspace is（x，y，θ）.the pose of the robot in the image plane is（xm，ym，θm）.Then，by using the state and input transformations in Section 2，a kinematic model with unknown visual parameters will be deduced in the following section.

Remark 1.The first formula H（θ0）on this page is a rotation matrix which is different from that denoted by R（θ0）in［16］.In our paper，H（θ0）is a matrix of anticlockwise rotation，but R（θ0）in［16］is a matrix of clockwise rotation.

2　Problem formulation

In this section，we will present an uncertain chained system by using（5）and using the state and input transformations for type（1，2）mobile robot with unknown visual parameters.Then，we will propose the tracking problem for the uncertain chained system and type（1，2）mobile robot.

For system（1），suppose sin（β2-β1）/=0，and consider（5）.We have［22］

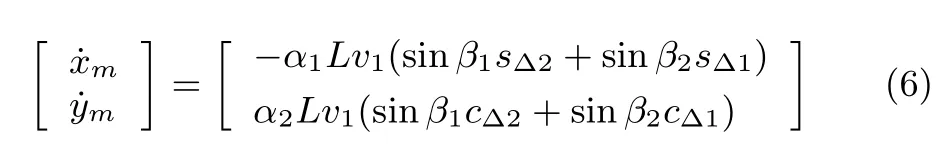
where

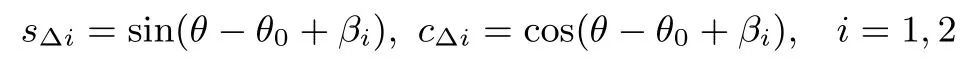
Considering kinematic system（1）in the robot workspace，we have

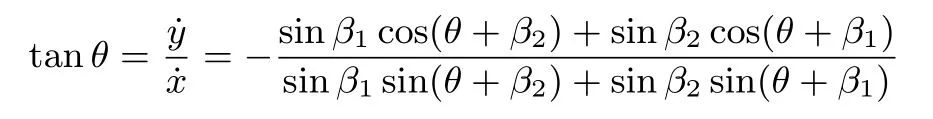
Then，

Now，considering（6）in the image space，we have

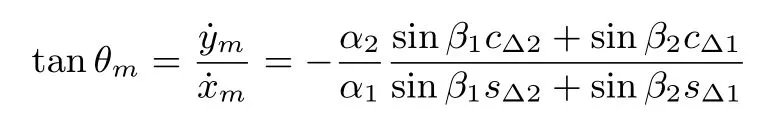
Hence，we obtain the following relationships

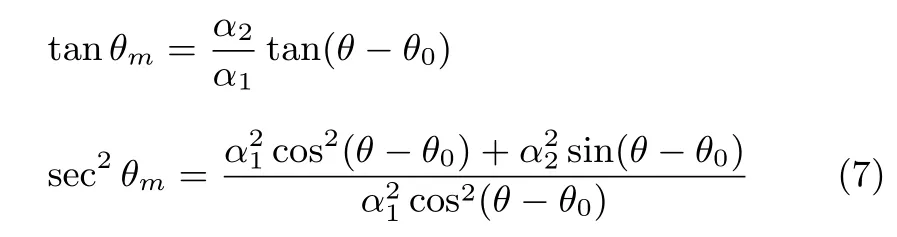
After taking the time derivative of（7），we have that

Therefore，we obtain

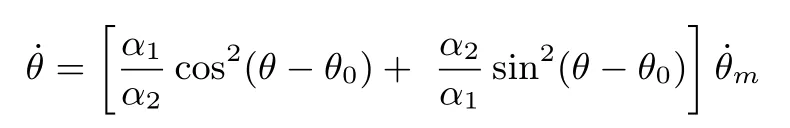
If α1=α2=α，we have˙θm=˙θ and θm=θ-θ0+kπ（k=0，±1，±2，···）.Then，the nonholonomic kinematic system with uncalibrated parameters in the image-plane can be described by the following system

where θmis expressed by θ.For i=1，2，denote

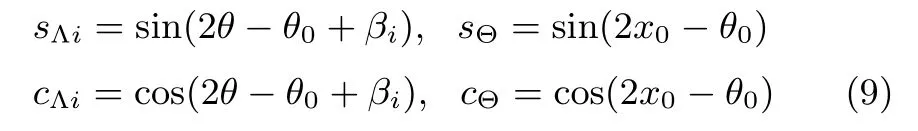
and consider the following expressions

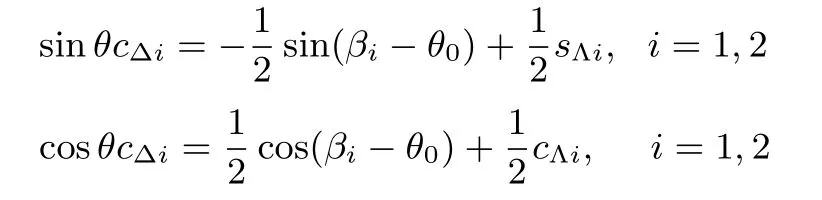
Then，note that

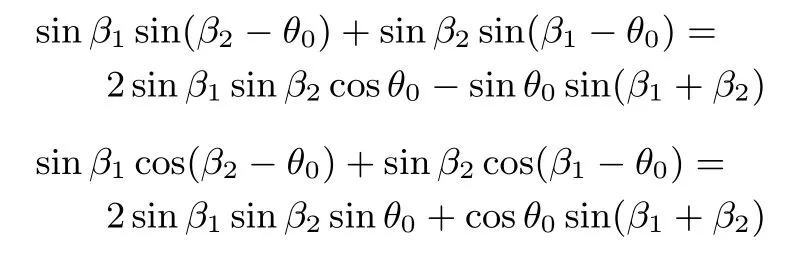
and

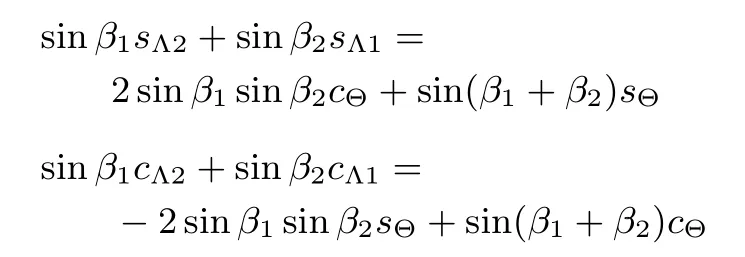
Hence，by taking the following state and input transformations

One obtains the uncertain chained system［22］

where u0=v1sin（β2-β1）and sin（β2-β1）/=0.

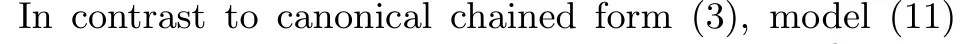
has two new parameters α and θ0.In practice，they are usually uncalibrated.Comparing with model（3），the first term on the right side of each equation of（11）is identical except uncertain coefficient gains.Note that the second and third terms on the right side of the second equation are dependent on x1，x2，x3and x4.Therefore，（11）does not satisfy the so-called triangular structure［8］which is required in many papers.So（11）is called an uncertain chained system.

For uncertain system（11），the tracking problem is how to design u0，u1and u2such that the trajectory（x0，x1，x2，x3，x4）can track a desired reference trajectory（x0r，x1r，x2r，x3r，x4r）.In the work-space of type（1，2）mobile robot，the adaptive dynamic tracking problem is how to design adaptive control law and dynamic feedback control to make the trajectory q=（x，y，θ）tracking a desired reference trajectory qr=（xr，yr，θr）in the work-space of the robot with the help of the reference trajectories in the image space.

3　Tracking controller design

In this section，our objective is to design adaptive dynamic feedback tracking controllers to solve the tracking problem for uncertain chained system（11）and the type（1，2）mobile robot in the work-apace.In order to design the controller，three Assumptions and a Lemma are needed as follows.

Assumption 1.Uncertain chained system（11）satisfies u0/=0.

Assumption 2.θ0is known，and α1=α2=α are unknown.There exist two constantsandα¯ such that

Assumption 3.xir（i=0，1，···，4）are bounded.u0r（u0r/=0），u1r，u2rand their derivatives are all bounded too.

Remark 2.System（11）is based on the assumption sin（β2-β1）/=0.This means u0/=0 for（11）.

Remark 3.For Assumption 2，α1=α2=α means that the scale factor along i1axis is the same with that one along j1axis.Some CCD cameras are made like this. However，α1=α2=α are limitations.As for the tracking problem of the case α1/=α2and unknown，we will further investigate it in the future.

Remark 4.Assumption 3 is rational.Commonly，the positive upper and lower bounds of the scale factor can be estimated in advance.In practice，the robot often has the same structure feature with a reference target when the robot tracks the reference trajectory.

Remark 5.Consider system（11）under Assumptions 1～3.By substituting θ-θ0for θ，（11）will become the system with θ0=0.This implies that the direction of j axis is identical to that one of X axis.Hence，we only need to discuss the case:θ0=0，α1=α2=α are unknown for（11）.

Based on the Assumptions 1～3 and the analysis above，system（11）can be rewritten as

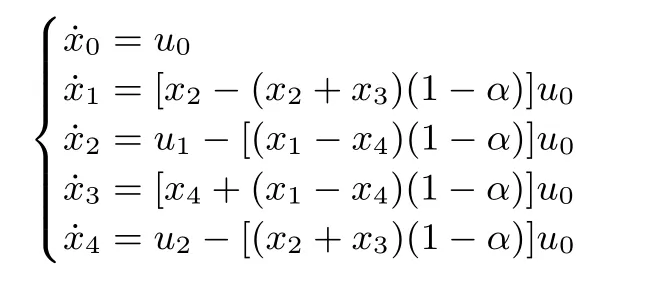
where α is the unknown camera parameter，u0，u1and u2are the control inputs to be designed.It can also be rewritten as

where

The desired reference system for（12）is

where

Denote

By using（12）and（13），the following kinematic tracking error system is obtained

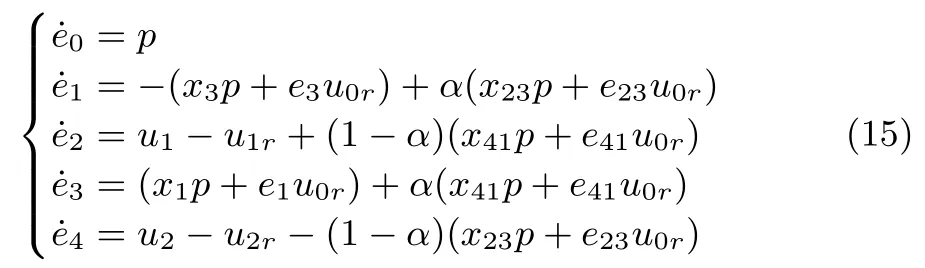
where p:=u0-u0r.

Based on the idea of backstepping and the structure of model（15），choose two new transformations as

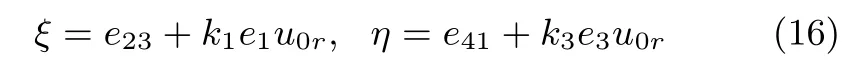
where k1and k3are positive constant control gains.Then，we have

Choose the Lyapunov function candidate

where k0is a positive constant gain.˜α is the parameter error defined as=α-.is the estimation of α.

By using（16），we have

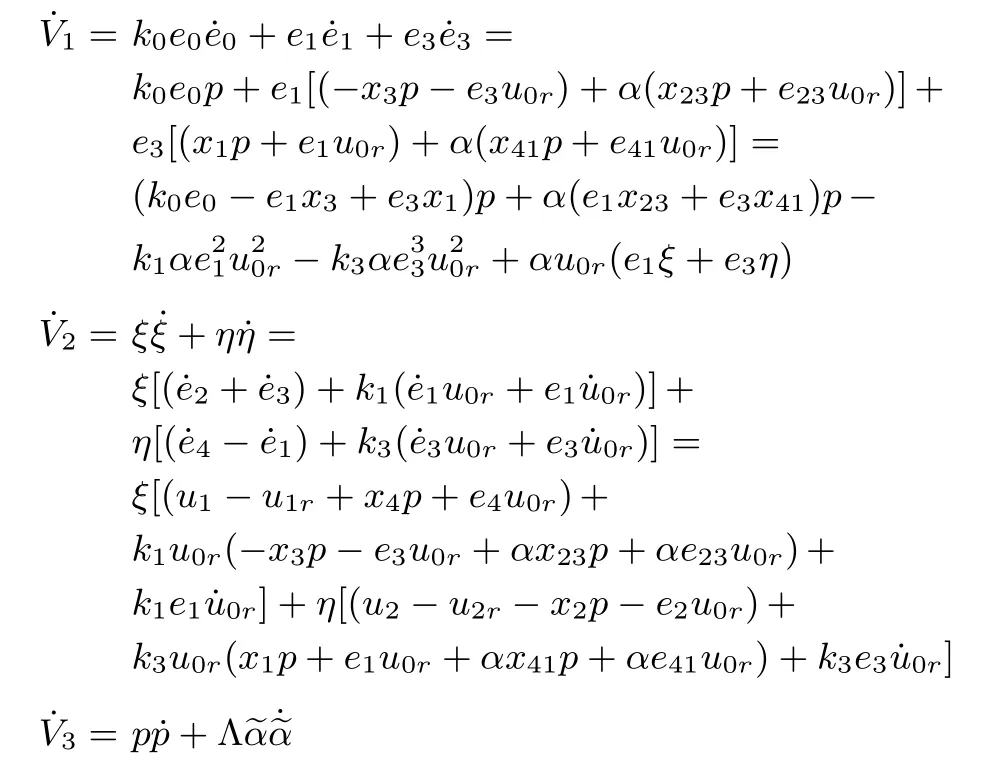
Hence，the time derivative of V along the solution of（15）satisfies

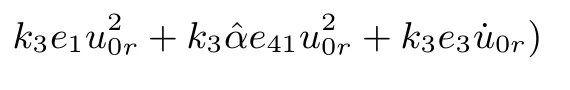
Take the adaptive law and dynamic feedback controller as follows

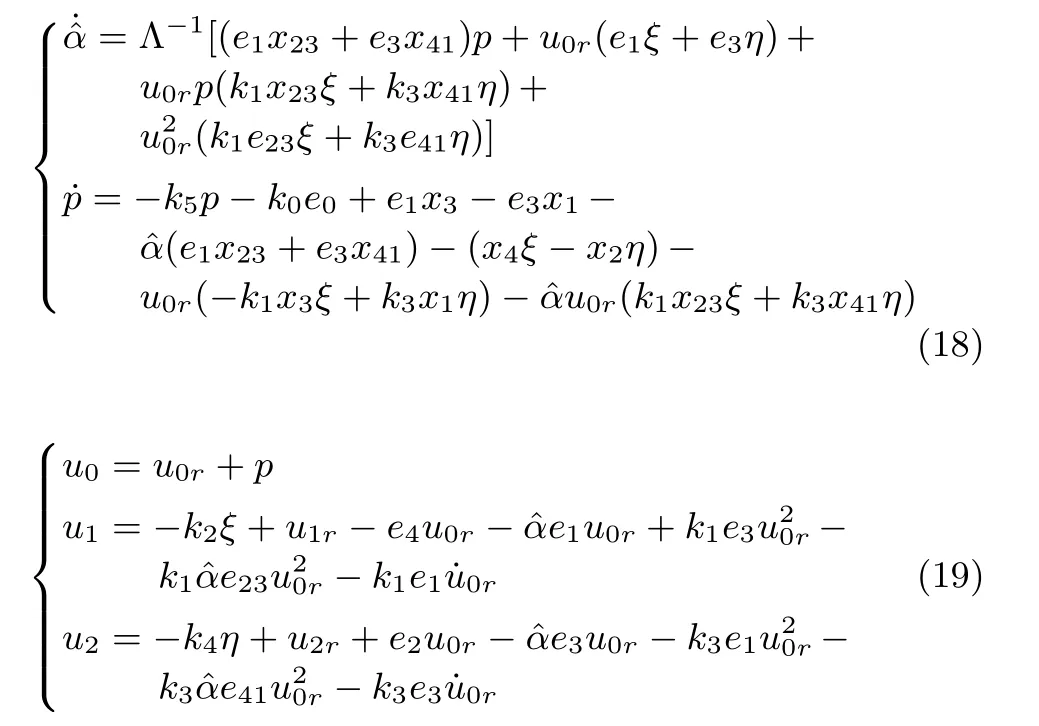
One obtains

where ki（i=1，2，3，4，5）are positive constant control gains.

Now，in order to prove the convergence of ei（i=0，1，2，3，4），an important lemma is introduced as follows.It is called“the extended Barbalat theorem”.Its proof was given in［23］.

Lemma 1.If the differentiable function f（t）has a finite limit as t→∞，and（t）can be divided into two parts，one is uniformly continuous and the other is convergent to zero as t→ ∞，then→ 0，and the part of the uniform continuity tends to zero，too［23］.

Theorem 1.Under Assumptions 1～3，the adaptive law（18）and dynamic feedback controller（19）can guarantee that all the variables of the closed-loop system（15），（18）and（19）are bounded.In addition，p and kinematic tracking errors ei（i=0，1，2，3，4）asymptotically converge to zero.

Proof.Considering（17），（20）and Assumptions 1～3，we find that the Lyapunov function V（t）is nonincreasing and converges to a limiting value（limV（t）≥ 0）.This means that e1，e3，ξ，η and p are all bounded.Then，e2，e4are all bounded too by using（16）.xi（i=1，2，3，4）are bounded further by Assumption 3.In view of（15），（18）and（19）again，we have˙ei（i=0，1，2，3）andare all bounded too.So，is uniformly continuous. By using Lemma 1，we obtain that˙V tends to zero and

Consider that u0ris bounded and u0r/=0 in Assumption 3.We have（e1，e3）→0 as t→∞.By the definitions of ξ and η，one obtains（e2，e4）→ 0 as t→ ∞.Using the Extended Barbalat Theorem in Lemma 1 on the second equation of（18），we have→0 and k0e0→0 where k0is a bounded control gain.Hence，we have ei→0（i=0，1，2，3，4）asymptotically as t→∞.

Remark 6.For the uncertain chained system（12），the tracking problem can be solved by using the control law u0，u1and u2.However，in practice，the controllers usually arev1，v2and v3in the robot running place for（1）or（8）.By using（8）and（10），they can be deduced as follows.

Theorem 2.Under the Assumptions 1～3，ei→ 0（i=0，1，2，3，4）ensure the trajectory（x，y，θ）of type（1，2）mobile robot in the task-place tracking the reference trajectory（xr，yr，θr）by using the controllers（18）and（19），or using control law（18），（19）and（21）.

Proof.For（10），we have

where H-1（θ0）=HT（θ0）.

Consider the second and forth equations in（10）.We have

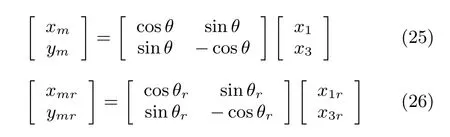
It is obvious that

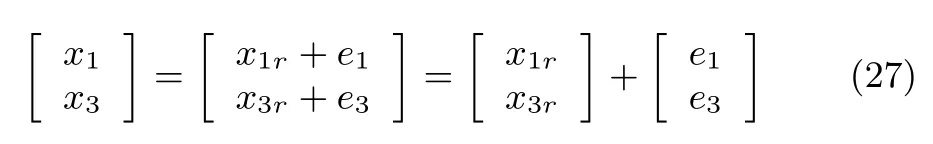
Substracting（26）from（25），we obtain the following relationship

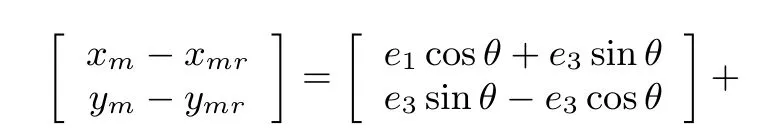
Then，for（24），we have

Note that θ=x0=x0r+e0=θr+e0.Then，we have θby relationships（28）and（29）.

To sum up，under the Assumptions 1～3，the trajectory（x，y，θ）for type（1，2）mobile robot in the task-space can track the reference trajectory of（xr，yr，θr）by using controller（18），（19）and（21）.Simulation results are addressed in the next section.

4　Simulation

In this section，the simulations have been implemented mainly for the states ei（i=0，1，2，3，4）of the error system（15），the adaptive law（18），the control law（19），the tracking errors=（xm-xmr，ym-ymr，θm-θmr）in the image frame，and the tracking errors（ex，ey，eθ）=（x -xr，y-yr，θ-θr）in the task-space for type（1，2）mobile robot.Two cases are considered for the different choices of the bounded control gains ki（i=0，1，2，3，4，5）.Given a sensor noise on the velocities，the tracking simulations results are also implemented and addressed in Case 3.

Case 1.Consider（12），（15），（18）and（19）.Then，take the initial error value［e0（0），e1（0），e2（0），e3（0），e4（0）］=［0.2，0.4，0.1，-0.2，0］for the configuration of（15）.Further，choose the parameters as θ0=π/3，u0r=0.1，u1r=1，u2r=1.5，k0=500，k1=12，k2=20，k3=15，k4=18，k5=20 and the control gain Λ=1.The trajectories of error states ei（i=0，1，2，3，4）and the control inputs ui（i=0，1，2）are plotted in Figs.2～4 respectively.The estimatesof the parameterand the dynamic feedback factor p are plotted respectively in Figs.5 and 6.In addition，the control laws v1，v2and v3in the task-space are also plotted in Figs.7 and 8 by using（12），（15），（19）and（21）.

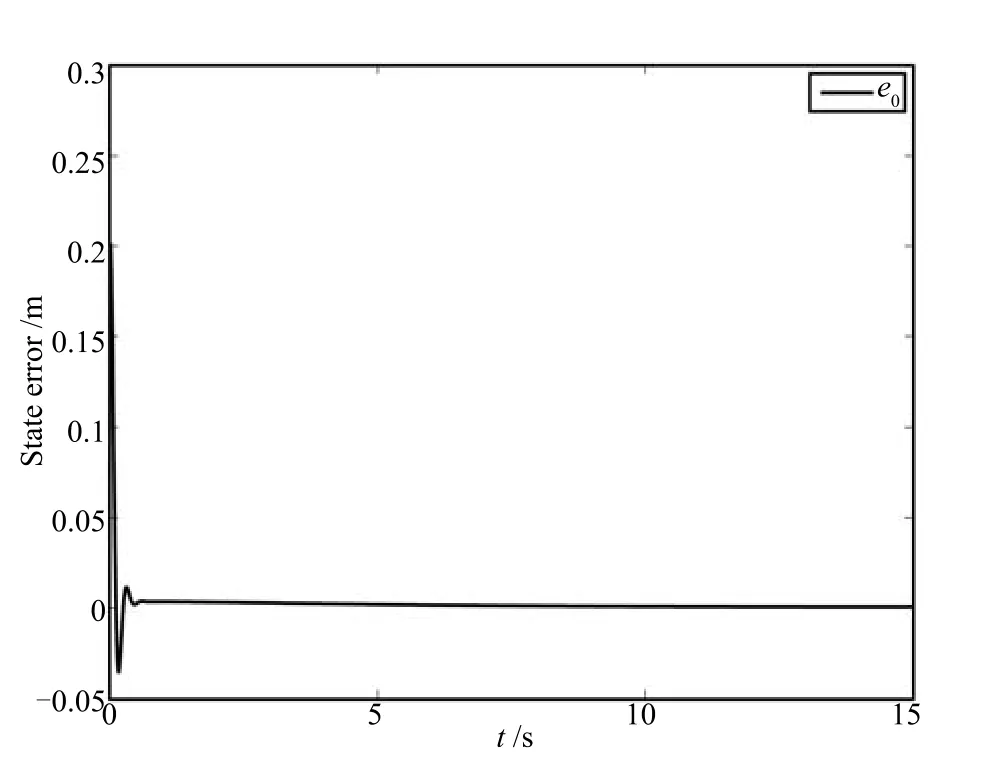
Fig.2　The trajectory e0with respect to time for Case 1

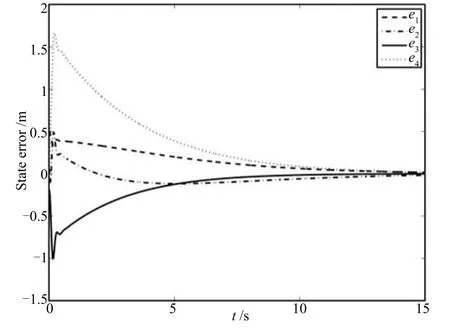
Fig.3　The trajectories of ei（i=1，···，4）for Case 1

Fig.4　The trajectories of ui（i=0，1，2）for Case 1

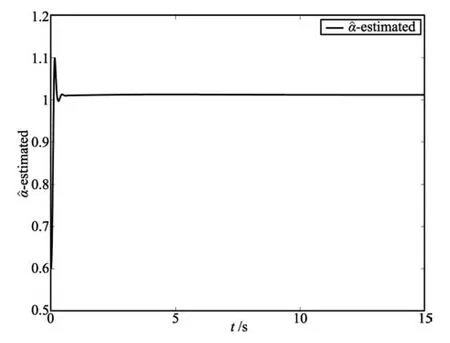
Fig.5　The trajectory ofwith respect to time for Case 1

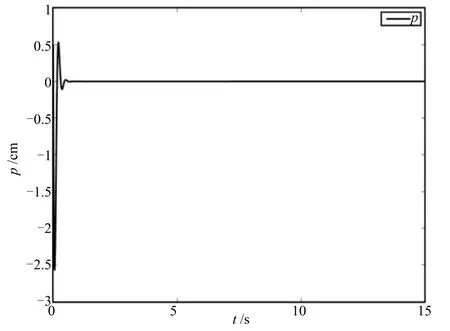
Fig.6　The trajectory of p with respect to time for Case 1

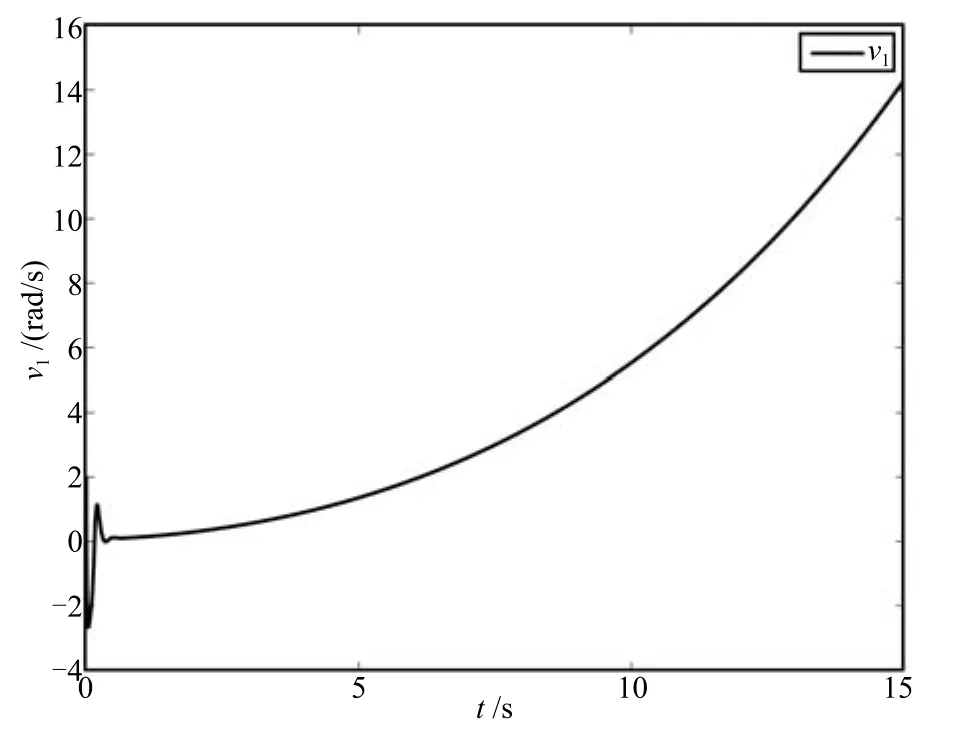
Fig.7　The velocity v1of the mobile robot for Case 1

Fig.8　The velocities v2and v3of the mobile robot for Case 1

Assume that the reference trajectory of the mobile robot in the image frame is chosen as xmr=2cosθr，ymr=sinθr.Then，x1r=cos2θr，x3r=cosθrsinθrby（22）.The tracking error trajectories for exm=xm-xmr，eym=ymymrand eθm=θm-θmrin the image space are presented in Fig.9.By using（4），（10），（15）and（29），the tracking error trajectories for ex=x-xr，ey=y-yrand eθ=θ -θrin the robot work-space are addressed in Fig.10.

Case 2.Given the initial error values［e0（0），e1（0），e2（0），e3（0），e4（0）］=［0.2，0.4，0.1，-0.2，0］.Then，the parameters such as θ0，u0r，u1r，u2r，α，Λ and the reference trajectory of the mobile robot in the image frame are the same as in Case 1.However，choose k0=900，k1=22，k2=30，k3=25，k4=38 and k5=50.Then，ei（i=0，1，2，3，4）areplotted in Fig.11.The tracking error trajectories forandin the image space are presented in Fig.12. The tracking error trajectories for ex，eyand eθin the robot work-space are addressed in Fig.13.

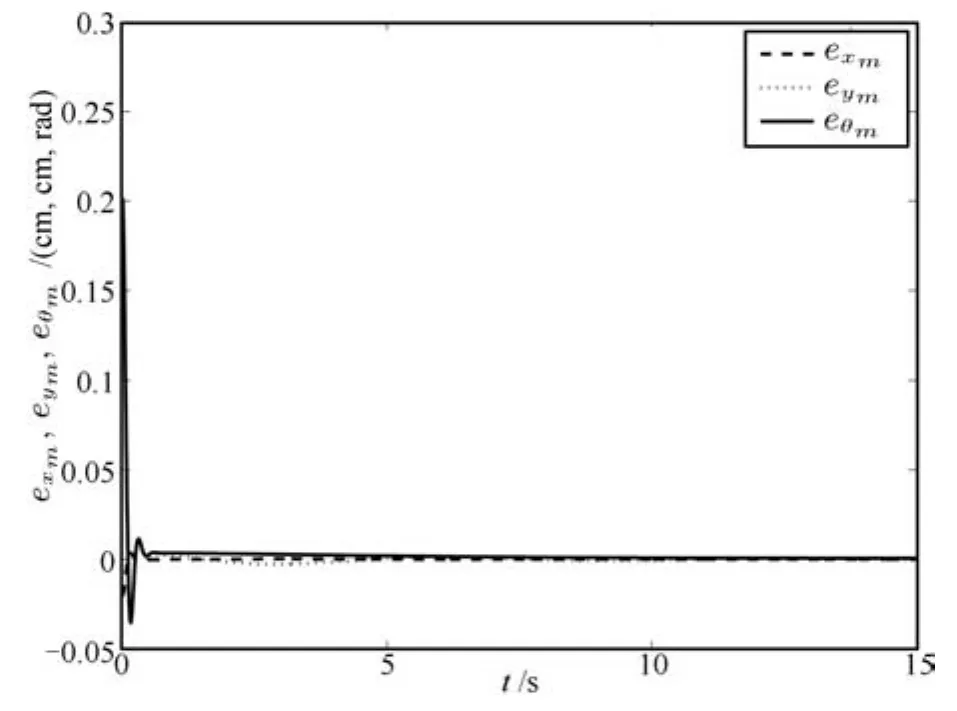
Fig.9　The tracking error trajectories for exm，eymand eθmin the image frame for Case 1

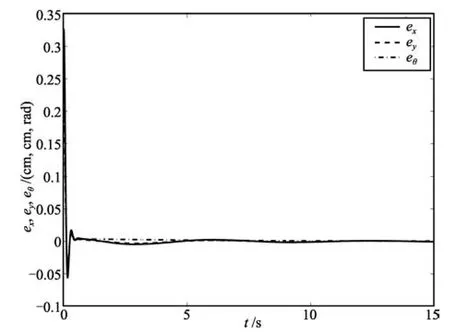
Fig.10　The tracking error trajectories for ex，eyand eθin the robot task-space for Case 1

Fig.11　The tracking errors in the robot task-space for Case 2

Case 3.For the type（1，2）mobile robot，assume v1=v2=v3=0 in the initial state.The initial values for system（8）are［xm（0），ym（0），θ（0），β1（0），β2（0）］=［0，0，0，0.2，0.1］.Given a sensor noise on the velocities∆v1=1，∆v2=2，∆v3=1.By using（8），we have［xm，ym，θ，β1，β2］=［0.0165，0.0042，-0.0046，0.4，0.2］when t0=0.1s（without loss of generality，t0is a finite constant）.Then，［x0，x1，x2，x3，x4］=［-0.046，0.0165，0.7831，0.0041，5.7007］by（10）.Take the reference trajectories in the image space xmr=2cosθr，ymr=sinθr.β1r=θrand β2r=2θr.Considering（22），the reference states are［x0r，x1r，x2r，x3r，x4r］=［0.05，1.9975，0.1498，0.0499，7.9775］when t0=0.1s.So，at this moment，we get new initial values［e0（t0），e1（t0），e2（t0），e3（t0），e4（t0）］=［-0.056，-1.9810，0.6333，-0.0458，-2.2096］.Choose the controllers（18）and（19）where k0=1200，k1=30，k2=40，k3=50，k4=46 and k5=100.Then，ei（i=0，1，2，3，4）converge to zero asymptotically.The trajectories are plotted in Fig.14. The tracking error trajectories for exm，eymand eθmin the image space are presented in Fig.15.The tracking error trajectories for ex，eyand eθare addressed in the robot work-space in Fig.16.

Fig.12　The tracking errors in the image frame for Case 2

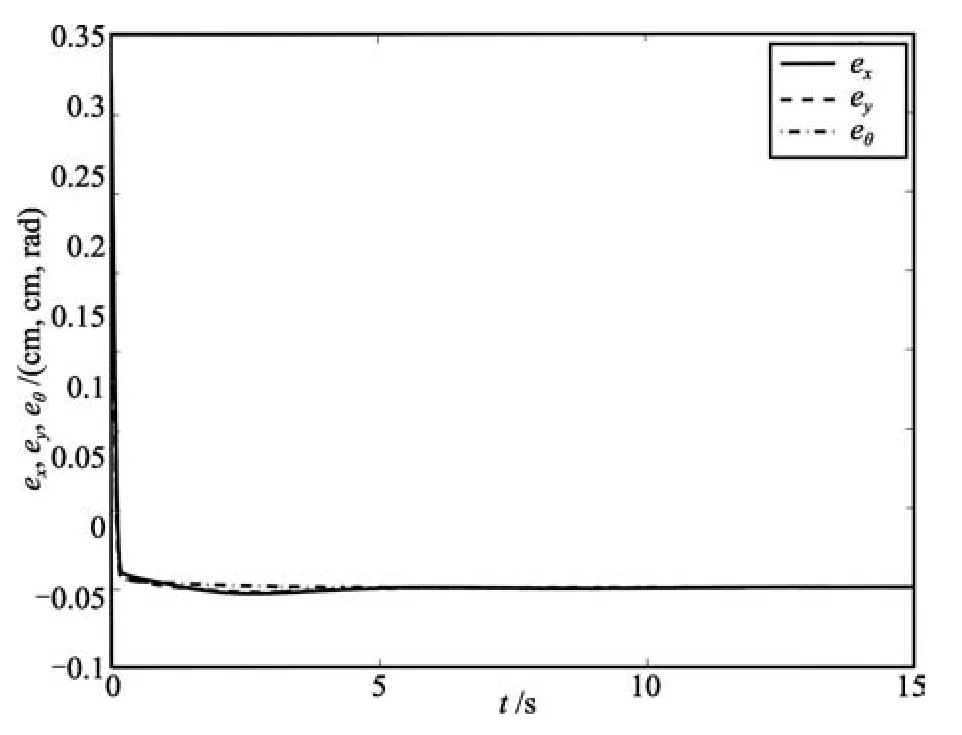
Fig.13　The tracking error trajectories for ex，eyand eθin the robot task-space for Case 2

Remark 7.Comparing the tracking errors in Case 1 with those in Case 2，we find that the bigger gains ki（i=0，1，···，5）make the better convergence.However，they could not be big enough in the practice.Considering the tracking control problems in［16］，an adaptive controller isdesigned to compensate for uncertain camera and mechanical parameters in the kinematic and dynamic systems for type（2，0）mobile robot.The tracking errors for X-coordinate and Y-coordinate converged to zero within ten seconds.In our paper，two transformations are exploited based on the idea of backstepping with the help of camerarobot system.An adaptive control law and dynamic feedback robust controllers are designed to track the desired trajectory for the type（1，2）robot by using Lyapunov direct method and the extended Barbalat Lemma.The tracking errors for X-coordinate and Y-coordinate can also converge to zero within 10 seconds（see Figs.12 and 13）.Simulation results（Figs.2～13）demonstrate the feasibility of the proposed adaptive and dynamic feedback laws.

Fig.14　The tracking errors in the robot task-space for Case 3

Fig.15　The tracking errors in the image frame for Case 3

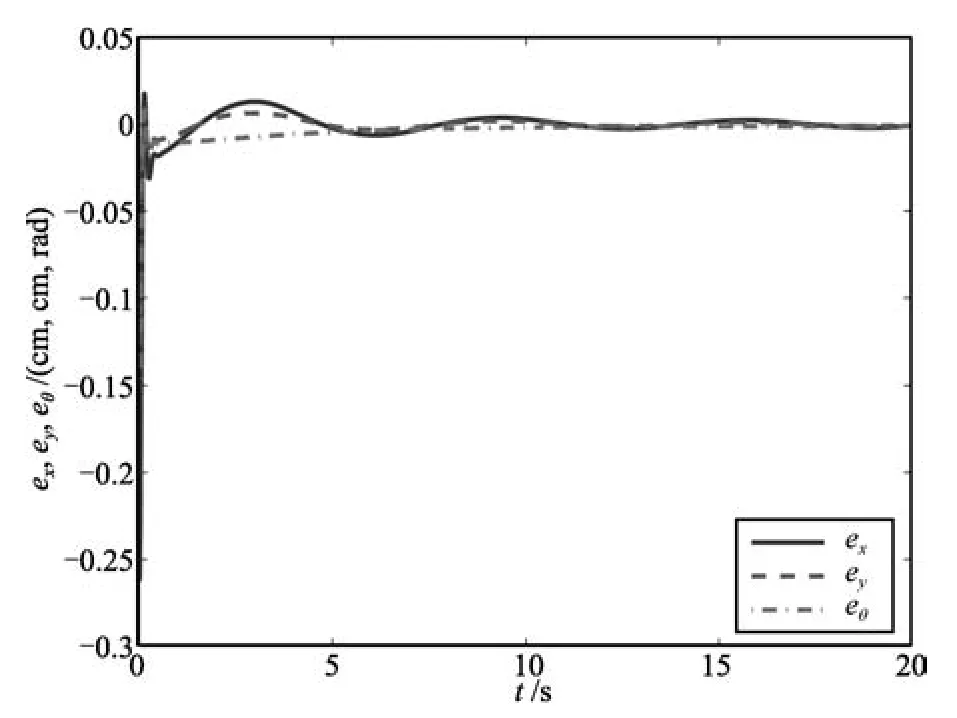
Fig.16　The tracking error trajectories for ex，eyand eθin the robot task-space for Case 3

5　Conclusions and future work

Based on the visual servoing feedback and the transformations for the canonical chained form of type（1，2）mobile robot，we present an uncertain chained model of nonholonomic kinematic system.Then an adaptive law and dynamic feedback controller has been proposed for the kinematic error system of the nonholonomic mobile robot. The asymptotical convergence of closed-loop error system is rigorously proved by Lyapunov stability theory and the extended Barbalat Lemma.Simulation results illustrate the performance of the proposed controller.

In this paper，the adaptive dynamic feedback tracking controller is investigated for known θ0，but α1=α2=α are unknown.As for other cases，such as θ0，α1and α2all unknown，they will be dealt with in the future.In addition，dynamics tracking control problems with uncertain parameters are not neglected，and we will further investigate them.

References

1 Kolmanovsky I，McClamroch N H.Developments in nonholonomic control problems.IEEE Control Systems Magazine，1995，15（6）:20-36

2 Wang C L.Semiglobal practical stabilization of nonholonomic wheeled mobile robots with saturated inputs.Automatica，2008，44（3）:816-822

4 Pang Hai-Long，Ma Bao-Li.Adaptive unified controller of arbitrary trajectory tracking for wheeled mobile robots with unknown parameters.Control Theory and Applications，2014，31（3）:285-292（in Chinese）

5 Cao K C.Global κ-exponential tracking control of nonholonomic systems in chained-form by output feedback.Acta Automatica Sinica，2009，35（5）:568-576

6 Ma B L，Tso S K.Unified controller for both trajectory tracking and point regulation of second-order nonholonomic chained systems.Robotics and Autonomous Systems，2008，56（4）:317-323

7 Campion G，Bastin G，Dandrea-Novel B.Structural properties and classification of kinematic and dynamic models of wheeled mobile Robots.IEEE Transactions on Robotics and Automation，1996，12（1）:47-62

8 Jiang Z P.Robust exponential regulation of nonholonomic systems with uncertainties.Automatica，2000，36（2）:189-209

9 Ma Bao-Li.Robust smooth time-varying exponential stabilization of dynamic nonholonomic mobile cart with parameter uncertainties.Acta Automatica Sinica，2005，31（2）:314 -319（in Chinese）

10 Wang C L，Liang Z Y，Jia Q W.Dynamic feedback robust stabilization of nonholonomic mobile robots based on visual servoing.Journal of Control Theory and Applications，2010，8（2）:139-144

11 Liang Z Y，Wang C L.Robust stabilization of nonholonomic chained form systems with uncertainties.Acta Automatica Sinica，2011，37（2）:129-142

12 Dong W J.On trajectory and force tracking control of constrained mobile manipulators with parameter uncertainty. Automatica，2002，38（9）:1475-1484

13 Wang Y N，Peng J Z，Sun W，Yu H S，Zhang H.Robust adaptive tracking control of robotic systems with uncertainties.Journal of Control Theory and Applications，2008，6（3）: 281-286

14 Allen P K，Timcenko A，Yoshimi B，Michelman P.Automated tracking and grasping of a moving object with a robotic hand-eye system.IEEE Transactions on Robotics and Automation，1993，9（2）:152-165

15 Do K D，Jiang Z P，Pan J.Simultaneous tracking and stabilization of mobile robots:an adaptive approach.IEEE Transactions on Automatic Control，2004，49（7）:1147-1152

16 Dixon W E，Dawson D M，Zergeroglu E，Behal A.Adaptive tracking control of a wheeled mobile robot via an uncalibrated camera system.IEEE Transactions on Systems，Man，and Cybernetics—Part B:Cybernetics，2001，31（3）: 341-352

17 Jia Bing-Xi，Liu Shan，Zhang Kai-Xiang，Chen Jian.Survey on robot visual servo control:vision system and control strategies.Acta Automatica Sinica，2015，41（5）:861-873（in Chinese）

18 Chen J，Dixon W E，Dawson M，McIntyre M.Homographybased visual servo tracking control of a wheeled mobile robot. IEEE Transactions on Robotics，2006，22（2）:406-415

19 Wang H S，Liu Y H，Zhou D X.Dynamic visual tracking for manipulators using an uncalibrated fixed camera.IEEE Transactions on Robotics，2007，23（3）:610-617

20 Wang C L，Mei Y C，Liang Z Y，Jia Q W.Dynamic feedback tracking control of non-holonomic mobile robots with unknown camera parameters.Transactions of the Institute of Measurement and Control，2010，32（2）:155-169

21 Yang F，Wang C L.Adaptive tracking control for dynamic nonholonomic mobile robots with uncalibrated camera parameters.In:Proceedings of the 8th Asian Control Conference.Kaohsiung，China:IEEE，2011.269-274

22 Liang Z Y，Wang C L.Robust exponential stabilization of nonholonomic wheeled mobile robots with unknown visual parameters.Journal of Control Theory and Applications，2011，9（2）:295-301

23 Samson C.Control of chained systems application to path following and time-varying point-stabilization of mobile robots.IEEE Transactions on Automatic Control，1995，40（1）:64-77

Liang Zhen-Ying，Wang Chao-Li，Chen Hua，Li Cai-Hong.Adaptive dynamic feedback tracking control for a robotcamera system with unknown parameters.Acta Automatica Sinica，2016，42（10）:1595-1604

10.16383/j.aas.2016.e110097

The control of nonholonomic systems has a great deal of attention over the past twenty years［1-2］.In［3］and some references therein，it is shown that many systems with nonholonomic constraints can be transformed，either locally or globally，to chained systems by using coordinate and state-feedback transformations.Several new control strategies were developed around the important nonholonomic chained models［4-6］.A wheeled mobile robot（WMR）is one of the well-known systems with nonholonomic constraints［7］.In the control of nonholonomic WMR，it is usually assumed that the states are available using sensor measurements.But in practice，there exist uncertainties，such as uncalibrated parameters in the kinematic models，mechanical limitations，noise and so on.In recent ten years，the study of nonholonomic systems with uncertainties has［8-11］.Adaptive strategies were often used to control the dynamic nonholonomic systems with modeling or parametric uncertainties［12-13］.

considerable attention.Many strategies have been investigated to stabilize the uncertain nonholonomic systems

Manuscript June 6，2015；accepted May 25，2016

Supported by National Natural Science Foundation of China（61374040，61304004，61473179），Scientific Innovation Program（13Z Z115），Hujiang Foundation of China（C14002），Graduate Innovation Program of Shanghai（54-13-302-102），and the Natural Science Foundation of Shandong Province（ZR2013FM012，ZR2014FM007）

Recommended by Associate Editor HOU Zeng-Guang

1.School of Science，Shandong University of Technology，Zibo 2550492.Optical-Electrical and Computer Engineering Department，University of Shanghai for Science and Technology，Shanghai 2000933.Mathematics and Physics Department，Hohai University，Changzhou Campus，Changzhou 2130224.School of Computer Science and Technology，Shandong University of Technology，Zibo 255049

LIANGZhen-Yingher Ph.D.degree from the Department of Control Science and Engineering，University of Shanghai for Science and Technology in 2011.She

her master degree and bachelor degree in mathematics from Liaoning Normal University in 1991 and Shandong Normal University in 1986，respectively.Currently，she is an associate professor at the Science School，Shandong University of Technology.Her research interest covers nonlinear controls，robust controls，and visual servoing feedback control.

of this paper. E-mail:lzhenying@126.com

WANG Chao-Lihis Ph.D. degree in control theory and engineering at Beijing University of Aeronautics and Astronautics in 1999，and

his master and bachelor degrees in applied mathematics at Lanzhou University in 1992 and 1986，respectively.Currently，he is a professor in the Department of Electrical Engineering，University of Shanghai for Science and Technology.His research interest covers nonlinear control，robust control，robot dynamic and control，visual servoing feedback control，and pattern identification.E-mail:clclwang@126.com

CHEN Huahis bachelor degree from the Department of Mathematics，Yangzhou University in 2001，

his master degree from the Department of Management Sciences and Engineering，Nanjing University in 2009，and

his Ph.D.degree from the Department of Control Science and Engineering，University of Shanghai for Science and Technology in 2012.Currently，he is an associate professor in the Mathematics and Physics Department，Hohai University，Changzhou Campus.His research interest covers saturated control for nonlinear systems，motion control of nonholonomic mobile robots，and analysis and control of fractional-order systems. E-mail:chenhua112@163.com

LI Cai-Hongher bachelor degree in automation from the School of Information Engineering，Southwest University of Science and Technology in 1993，and

her master degree in control theory and control engineering from the College of Information Science and Engineering，Shandong University of Science and Technology in 2000.She

her Ph.D.degree in detection technique and automatic device from the School of Control Science and Engineering，Shandong University in 2007.Currently，she is a professor at the College of Computer Science and Technology，Shandong University of Technology.Her research interest covers intelligent mobile robot，artificial intelligence in the mobile robot，coverage path planning for the mobile robot，and the applications of chaotic theory in the path planning. E-mail:lich@sdut.edu.cn