一种基于因子图模型的半监督社区发现方法

黄立威　李彩萍　张海粟　刘玉超　李德毅　刘艳博

一种基于因子图模型的半监督社区发现方法

黄立威1李彩萍1张海粟2刘玉超3李德毅4刘艳博1

社区发现是社交网络分析中一个重要的研究方向.当前大部分的研究都聚焦在自动社区发现问题，但是在具有数据缺失或噪声的网络中，自动社区发现算法的性能会随着噪声数据的增加而迅速下降.通过在社区发现中融合先验信息，进行半监督的社区发现，有望为解决上述挑战提供一条可行的途径.本文基于因子图模型，通过融入先验信息到一个统一的概率框架中，提出了一种基于因子图模型的半监督社区发现方法，研究具有用户引导情况下的社交网络社区发现问题.在三个真实的社交网络数据（Zachary社会关系网、海豚社会网和DBLP协作网）上进行实验，证明通过融入先验信息可以有效地提高社区发现的精度，且将我们的方法与一种最新的半监督社区发现方法（半监督Spin-Glass模型）进行对比，在三个数据集中F-measure平均提升了6.34%、16.36%和12.13%.

社交网络，半监督社区发现，因子图，社交网络分析，概率推理

引用格式黄立威，李彩萍，张海粟，刘玉超，李德毅，刘艳博.一种基于因子图模型的半监督社区发现方法.自动化学报，2016，42（10）:1520-1531

社交网络中，用户由于共同的兴趣和特征结成群体，群体体现了关系的局部聚集特性.在网络科学研究中，人们把用户视为节点，关系视为边，群体视为社区［1］.社区通常由功能相近或性质相似的网络节点组成，在一定程度上反映了用户自发、无序行为背后的局部弱规则性和全局有序性.对社交网络的社区结构的深入研究不仅有助于揭示相对独立而又相互关联的社区如何形成错综复杂的社交网络，帮助人们更好地理解系统在不同层次上的结构和功能特性，而且具有很多的实用价值，例如通过发现网络中的社区揭示具有共同兴趣或相似社会背景的社会团体.因此，社区发现已成为社交网络分析领域中一个非常重要的研究方向.

目前大部分社区发现的研究都是面向自动社区发现问题，即根据网络结构，通过算法自动地发现网络中的社区，是一种无监督的方法.但自动的社区发现通常存在两个重要的问题：

1）在面对具有链路缺失或具有噪声数据的网络时，自动社区发现的性能会大大下降［2］，很难有效地揭示网络中的真实社区结构；

2）类似于流行的模块度优化的社区发现方法［3］，通过近似优化方法最大化模块度来发现社区，通常得不到最优的社区划分［4］.

导致第一个问题的原因通常是，社区发现的时候仅仅考虑了当前的网络信息，其前提是将网络作为一个正确的、完全的网络处理，但通常情况下，我们获得的网络包含了大量包括错误连接在内的噪声数据，网络连接通常也是不完全的.在这样的情况下，即使最好的自动社区发现方法在遇到具有噪声的网络时其性能也会急剧下降.第二个问题是由于通过优化方法最大化模块度得到的是一个近似解，导致发现的社区是多种多样的，即使模块度的值差得很小，也可能导致差异非常大的社区划分，不能得到一个最优的划分结果，也很难发现特定情境下满足特定需求的社区结构.

在数据挖掘领域，针对具体的任务，往往会考虑加入用户引导或约束到挖掘任务中，提高数据挖掘的性能.事实上，在社交网络环境下，已知部分社区划分信息的情况也普遍存在，例如我们可能已知部分用户属于某一个社区，或者已知两个用户属于相同或不同的社区.通过将这些信息融入到社区划分中，进行半监督的社区发现，往往可以有效提高社区划分的准确度，提高噪声环境下社区划分的鲁棒性，而且还能帮助发现满足特定需求的社区划分.

在本文中，我们针对两种类型的先验信息，即已知部分节点的社区划分以及用户之间存在的成对的必须连接约束（Must-link constraints）和不能连接约束（Cannot-link constraints），研究半监督社区发现问题，提出了一种基于因子图模型的半监督社区发现方法，将原始的社交网络与两种先验信息融合到一个统一的半监督概率框架中，既可以使得发现的社区满足先验条件，又可以符合网络的整体社区结构.本文提出的模型具有高的适应性，因为通过定义更高阶的因子特征函数，我们可以将两个以上节点之间的约束融合到社区发现问题中.文献［5］研究了利用因子图模型进行社区发现的问题，但并没有考虑先验信息.据我们所能得到的信息，本文是第一次从概率推理的视角研究半监督社区发现问题，或许能够为我们进一步探索社区发现的不确定性提供一些有用的启发.

1　相关工作

2002年，Girvan和Newman［6］提出一种分裂式层次聚类方法，简称GN算法.在该方法中，作者为网络中的每条边定义了一个边介数（Edge betweenness）的量，一条边的边介数定义为网络的所有最短路径中经过该边的路径数目占最短路径总数的比例.边介数反映了相应的边在整个网络中的桥接作用，当按照边介数由高到低依次删除边时，网络分裂的速度要远快于随机删除连边时的网络分裂速度.因此，Girvan等提出一个迭代过程，每次迭代过程中通过计算网络中每条边的介数然后去除介数最大的边，一直到网络中所有的边被去除，每个节点自成一个社区，迭代过程停止.这种方法面临的困难在于切割位置的选择，即选择合并或分裂停止的时机，该问题的本质在于缺乏一种度量网络划分质量的有效手段.为解决网络划分质量度量这一本质问题，Newman等提出了著名的模块度（Modularity）的概念［3］.模块度选择一个假定不存在社区结构的网络（一般使用配置模型产生）作为参照网络，给定一个网络划分，通过对比原有网络和参照网络中处于该划分的各个分量内部边的比例，给出一种度量网络划分质量的手段.一般认为，对于同一个网络的不同划分，模块度越高，该划分越能体现网络固有的社区结构.如此一来，网络社区发现问题变成了一个模块度优化问题，即从网络的所有可能划分中寻找一个划分，使该划分具有最大的模块度，该划分的各个分量视为社区.模块度的提出很大程度上推动了社区发现的研究，研究人员开始探索基于模块度优化的算法.Brandes等指出模块度优化问题是一个NP难问题［7］，因此，人们引入各种启发式的模块度优化方法，如贪婪算法［8］、极值优化方法［9］、模拟退火［10］和谱聚类［11］等.

目前模块度优化方法已成为复杂网络社区发现的基准方法，并得到广泛的应用.然而，进一步的研究发现模块度优化方法在处理各种具体网络时存在一些问题：1）文献［12］发现由于随机波动模块度方法中所采用的参照网络也会呈现出伪社区结构，从而对模块度方法中采用参照网络提出了质疑，并基于统计显著性给出了相应的改进办法；2）文献［13］指出对于给定的网络，模块度优化方法存在一个固有的分辨率，使得模块度优化方法不能识别出该分辨率以下的社区，这就是所谓的“分辨率限制”问题.因此，小社区往往会被大的社区吸纳，从而淹没在大的网络社区中而无法被识别出来；3）文献［14］发现模块度优化方法不能很好地处理节点度分布高度差异的网络，而真实网络中的节点度分布往往服从幂率分布，研究通过引入尺度（Rescaling）变换解决了该问题.

进一步的研究表现，真实世界中的网络社区之间普遍存在重叠节点，这些节点在不同社区间起着桥梁作用，在社区中发挥着重要影响，是社区间信息扩散的媒介和社区演化的推手.鉴于这个问题，人们开始着眼于重叠社区结构的研究.最初，Palla等在Nature上发表论文［15］，指出了社区重叠这一重要现象，并提出了一种基于完全子图渗流（Clique percolation）的重叠社区发现方法.随后，该算法被扩展应用到有向网络、有权网络和二部网络等.直到现在，完全子图渗流算法依然是重叠社区发现研究中应用最为广泛的方法之一.

社区演化是社区发现研究中的另一个重要问题.演化是真实网络所具有的基本特性，社区演化是网络自身结构和在其上频繁发生的交互过程相互作用的结果.社区演化分析主要研究社区随时间变化的情况，并分析导致社区演化的原因以及内在的机制.文献［16］基于他们提出的完全子图渗流社区发现方法研究社区演化，得到一个有趣的结论：小社区的稳定性是保证其存在的前提，而大社区的动态性是其存在的基础.文献［17］通过扩展模块度研究异构关系网络中随时间演化的、多尺度社区结构.更多社区发现的研究可以参考文献［1］.

目前半监督社区发现的研究还较少.事实上，半监督社区划分与传统数据挖掘中的半监督聚类密切相关，Ma等［18］通过组合对称的非负矩阵因子分解和半监督聚类方法，融合成对的约束进行半监督社区发现.Allahverdyan等［19］通过融合部分已知的社区标签到社区发现中，分析了先验信息对于社区发现的影响.Eaton等［2］分别考虑已知部分社区标签和成对约束的两种情形，提出一种半监督的Spin-Glass模型，进行社区发现，可以有效地抵消噪声带来的影响.Liu等［20］提出了一种基于离散势理论的半监督社区发现算法，考虑了已知部分节点社区标签的先验信息.Li等［21］提出一种基于极值优化的半监督社区发现方法，这种方法利用了成对节点之间的社区约束信息.Yang等［22］基于隐空间相似性提出一种统一的半监督框架，可以在多种社区发现模型中融入社区先验信息.针对半监督信息难以获取的问题，Yang等［23］提出一种主动链路选择框架，研究了如何标注最不确定或最具信息量的先验信息，从而可以通过更少的先验信息达到相同的社区发现效果.但以上的研究中，都没有考虑同时融合多种先验信息的情形，本文提出的方法可以同时融入多种先验信息到一个统一的概率框架中，并通过优化方法确定不同的信息的权重.

2　问题定义

为了融合先验信息到社区发现中，我们基于因子图模型，对社交网络中的半监督社区发现问题进行建模，提出一种基于因子图的半监督社区发现方法（Factor graph-based semi-supervised community detection，FG-SSCD）.为了更清晰地对问题进行描述，首先我们给出社区发现的定义：

定义1（社区发现）.给定社交网络G=（V，E，A，Y）以及期望的社区集合L=｛l1，l2，···，lK｝，其中V是所有用户的集合，|V|=N，E⊂V×V是所有用户关系的集合，A是网络对应的邻接矩阵，Y是所有用户的社区标签，在一般的社区划分问题中，它在初始阶段是未知的，L表示所有社区标签集合.社区发现的目标是为每个用户vi确定其社区标签yi，yi∈｛l1，l2，···，lK｝，表示vi属于的社区.

在半监督社区发现问题中，通常考虑两种形式的先验知识：1）已知部分节点的社区标签；2）成对节点之间的必须连接和不能连接约束.在两种先验信息之间不存在冲突的前提下，本文研究的问题是如何同时考虑这两种信息，将其融入到一个统一的概率模型中，引导我们进行半监督社区划分.因此可以给出本文研究的半监督社区发现问题的定义.

定义2（半监督社区发现）.给定社交网络G=（V，E，A，Y），期望的社区集合L=｛l1，l2，···，lK｝，必须连接约束的集合M=｛（xi，xj）｝和不能连接约束的集合C=｛（xi，xj）｝，约束侵犯代价矩阵W 和其代表每个约束被侵犯需要付出的代价，也可以理解为每个约束的重要性权重，以及部分已知的用户社区标签YL和未知的用户社区标签YU，满足YU∩YL=∅，YU∪YL=Y.半监督社区发现的目标是针对未确定社区划分的用户vi，预测它们的社区标签yi，yi∈｛l1，l2，···，lK｝，即vi所属于的社区.

此外，针对每个社区lk存在一个变量集合Xk，用于表示社区lk中的用户集合.

3　基于因子图模型的半监督社区发现方法

3.1模型建立

在本节中，考虑融合先验信息到社区划分问题中，借鉴Tang等［24］提出的部分因子图模型的思想，建立一个基于因子图的半监督社区发现模型FGSSCD，将半监督的社区发现问题建模到一个统一的框架中.

本文接下来给出FG-SSCD模型的一个简单例子.如图1所示，左侧的图展示了一个网络示例，包含了5个用户｛v1，v2，···，v5｝以及相应的社会关系.右侧的图是由左侧的网络作为输入所建立的FG-SSCD模型，图中观测变量是网络中给定的用户｛v1，v2，···，v5｝，模型的隐变量即每个用户的社区标签｛y1，y2，···，y5｝，假设整个网络中的用户划分为两个社区，即社区标签为｛1，2｝，网络中已知用户v1，v2，v5的社区标签，分别为1，1，2，需要预测用户v3，v4的社区划分.为了对模型进行更加清晰的描述，下面对模型的基本要素分别进行详细介绍：

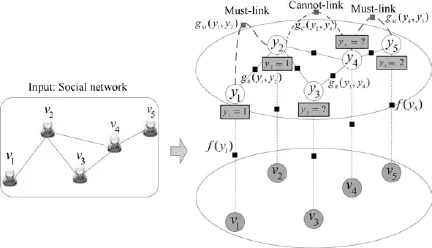
图1　FG-SSCD模型的图结构Fig.1　Graphical structure of FG-SSCD

1）变量节点

模型中包含了两类变量节点，分别为：隐变量和观测变量.

隐变量节点：模型中包含一个隐变量的集合｛y1，y2，···，yn｝，是不能直接观测到的，在图中用白色的圆圈表示，代表每个用户vi的社区标签，是问题需要预测的值.

观测变量节点：模型中包含一个观测变量的集合｛v1，v2，···，vn｝，在图中用灰色的圆圈表示，每一个观测变量由条件概率分布P（vi|yi）所产生，在模型中，当给定社区划分的情况下，随机变量V的产生是条件独立的，即

2）因子节点

根据用户自身的特征，用户之间存在的社会关系以及在社区发现中的约束，可以在模型中定义相关的因子函数：

节点特征因子：f（yi）是定义在单个隐变量上的节点特征因子，其表示在给定节点社区标签yi产生观测数据vi的概率P（vi|yi）.

关联特征因子：g（yi，yj）是定义在节点对之间的关联特征因子，反映了隐变量之间存在的关联，在本文模型中，仅仅考虑了成对的关联，根据不同类型的关联，定义了三类关联特征因子gR（yi，yj）、gM（yi，yj）和gC（yi，yj）·gR（yi，yj）表示用户之间由于存在的社会关系所定义的关联特征函数，gM（yi，yj）是根据用户之间存在的必须连接约束所定义的关联特征函数，gC（yi，yj）是根据用户之间存在的不能连接约束所定义的关联特征函数，我们将gM（yi，yj）和gC（yi，yj）也称为约束势函数.

根据Hammersley-Clifford定理［25］，一个具体的社区标签配置的概率能够使用吉布斯分布［26］所表示，因此我们可以得到：

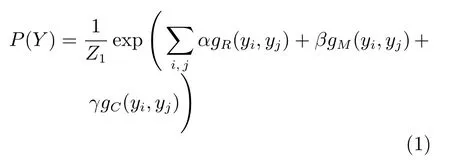
其中，α，β，γ分别表示特征函数gR，gM和gC所占的权重，Z1是归一化因子，也称为划分函数（Partition function），其形式为：

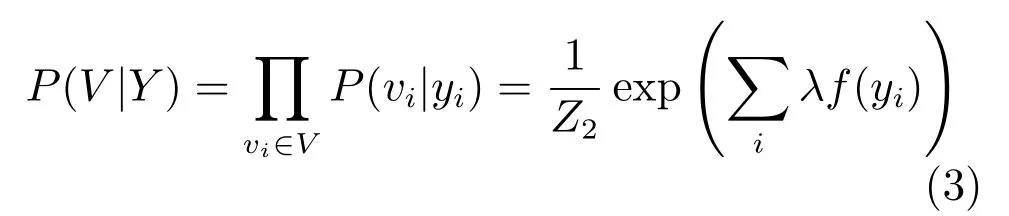
同样，λ表示特征函数f的权重，Z2是归一化因子，其形式为：

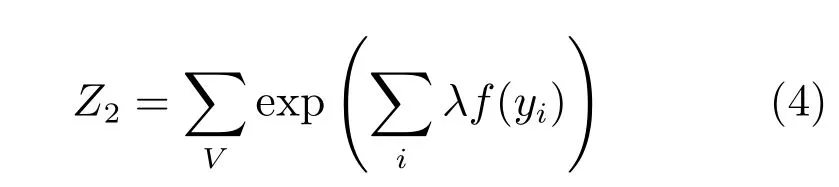
根据贝叶斯理论，条件概率分布P（Y|V）可以表示为：

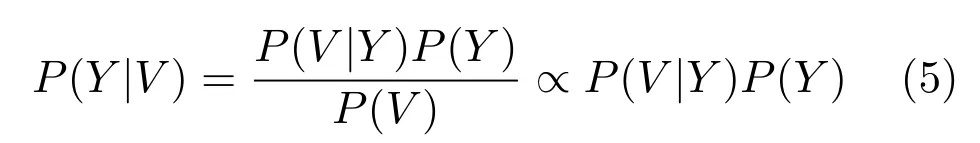
结合式（1）和（3），可以进一步得到：

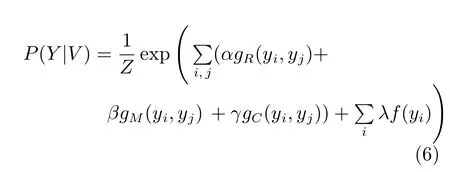
其中，用θ=｛α，β，γ，λ｝表示所有参数的集合，Z是归一化因子，可以表示为：

3.2因子函数定义

在给出模型的通用框架之后，我们进一步对模型中的因子函数进行定义.

我们针对网络中的每条边（yi，yj）定义一个边特征函数gR（yi，yj），用于表示边上的（即有关联的）两个节点选择同一个社区的可能性.其取值不仅仅与用户之间的关系权重有关，而且与每个用户的邻居个数有关，借鉴文献［5］中对边特征函数的定义，我们将其定义为：

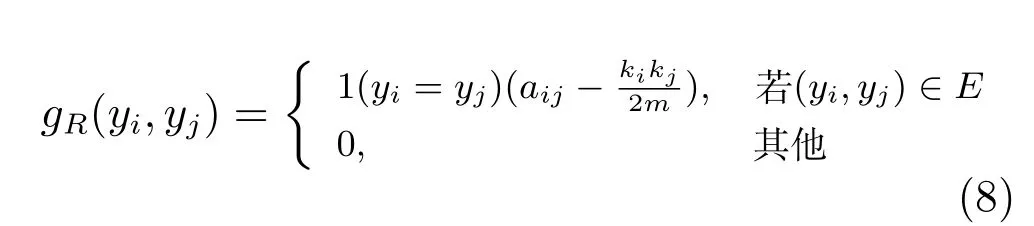
其中1（·）是指示函数，即如果对应的条件满足则函数取值为1，否则取0.其中ki是节点vi与所有邻居的边的总权重，即是节点vi的邻居集合，m是网络的总权重，即从定义可以看出，边特征函数gR（yi，yj）具有如下直观的含义：如果两个节点之间的权值越大，且两节点与它们各自邻居的权重相对网络的总权重越小，则两节点属于同一社区的概率越大.不难发现，gR（yi，yj）的定义事实上是借鉴了模块度的定义.

对于先验信息中的约束条件，我们定义了两种关联特征函数gM（yi，yj）和gC（yi，yj），借鉴Basu等［27］在使用隐马尔科夫随机场（Hidden Markov random field，HMRF）进行半监督聚类时选择Potts势［28］定义约束势函数的方式，将gM（yi，yj）和gC（yi，yj）分别定义为：

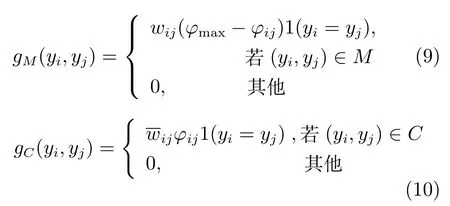
其中ϕij为用户vi，vj在网络中的距离，通常可以是最短路径，本文使用随机游走路径，ϕmax为网络中的节点最大距离.本文在约束关联特征函数中考虑了用户之间的距离，因为如果两个用户距离很近，他们更可能属于同一个社区，应该以更大的概率满足必须连接约束条件，以及更小的概率满足不能连接约束条件；反之亦然.因此对二者的定义正好可以确保社区划分以更大的概率满足约束条件.

根据模块度的定义，通过将所有边特征函数gR（yi，yj）的乘积最大化足以保证社区结构达到与模块度最优化相同的最大显著性，但是由于通过这种方式得到的各个社区之间并无差别，该算法并不能反映每个用户的主体行为.因此，我们通过定义节点特征函数，描述了一个节点vi选择加入某个社区的可能性，反映了用户自身的主体性.代替考虑用户与用户所属社区中的所有用户的相似度，我们简单地使用其相邻用户所属于的社区来反映单个用户的社区偏好：

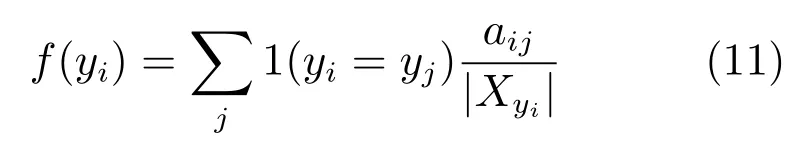
从定义可以看出，节点具有更大的概率与其更亲密的邻居具有相同的社区标签.我们注意到节点特征函数中的变量yi和|Xyi|的值应该直到整个网络的社区划分确定后才能被获得，因此我们简单地使用｛yi｝的中间结果计算节点特征函数.因此一旦yi和|Xyi|的值确定之后，节点特征函数都是常量.

3.3参数估计

接下来我们需要对模型中的参数θ=｛α，β，γ，λ｝进行评价.在我们的问题中，已知部分用户的社区划分，需要预测剩余用户的社区划分.我们需要通过整个网络的结构，融合成对用户之间的约束，部分用户的社区标签，来决定整个网络的社区划分.这里，我们使用Y|YL表示由部分用户标签推导而来的一个社区划分，通过采用log最大似然估计方法，得到log似然目标函数l（θ），如式（12）所示.

最大化目标函数，便可以获得估计的参数配

置θ∗，即：

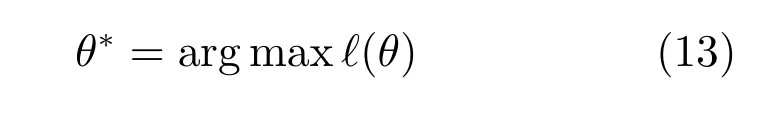
在本文中，我们采用梯度下降方法，对参数进行优化，参数的更新过程为：

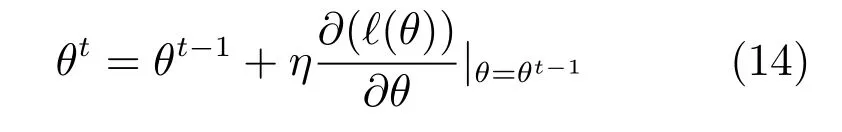
其中，η为所有参数θ的迭代步长，以λ为例，针对目标函数求λ的偏导数，如式（15）所示.

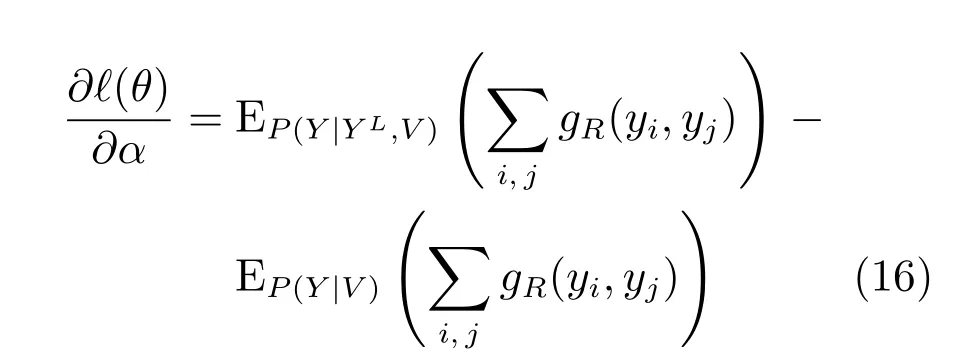
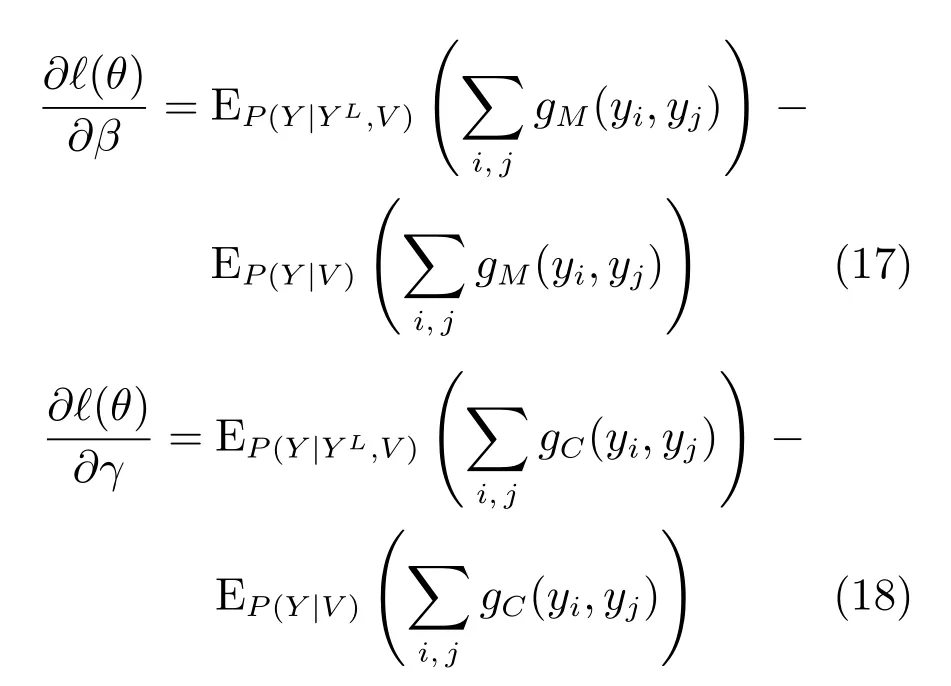
为了计算梯度，需要计算边缘概率分布 P（yi，yj|YL，V），P（yi|YL，V），P（yi，yj|V）和P（yi|V）.由于需要计算归一化因子Z，使得计算精确的期望值非常困难.此外，模型中的图结构是任意的，可能包含环路，因此本文选择迭代信念传播算法（Loopy belief propagation，LBP）［29］来近似计算梯度值.此外，我们针对每个用户vi定义的节点特征因子f（yi），不仅仅取决于yi的值，而且与其相邻的用户的社区划分以及vi所属社区的大小相关，这就导致我们在计算f（yi）的时候需要整个网络的社区划分，但这是本文需要求解的问题，这两者之间是矛盾的.针对这个问题，我们采取了一种近似方法.在模型训练的初始阶段，对于网络中未知社区划分的用户，我们采用K最近邻居方法，选择与其距离最近的K个用户的社区标签，来决定用户的初始社区划分，然后计算每个用户的节点特征因子f（yi），对于K值的选择，通常根据网络的规模、网络的稀疏程度，以及已知社区划分的用户在网络中的分布决定.而在使用LBP计算期望的每次迭代过程中，我们既使用Sum-product方法计算节点的边缘概率P（yi，yj|YL，V），P（yi|YL，V），P（yi，yj|V）和P（yi|V），又使用Max-product计算整个网络中隐变量的当前最佳配置Y∗，从而得到中间阶段整个网络的社区划分，然后重新计算每个用户的节点特征因子f（yi），即每次迭代之后，f（yi）的值随着社区划分的改变而变化.参数估计的具体过程如算法1所示.

算法1.FG-SSCD模型的参数学习算法

输入.社交网络G=（V，E，A，Y），期望的社区集合L=｛l1，l2，···，lK｝，已知的用户社区标签YL，必须连接约束的集合M=｛（xi，xj）｝和不能连接约束的集合侵犯约束代价W 和以及学习速率η；

输出.模型参数θ=｛α，β，γ，λ｝

算法步骤:

对于每个未知社区标签的用户，用K最近邻居方法初始化社区标签YU，计算f（yi）初始化θ

重复

1）使用LBP计算各个期望值

3）按照下式，使用学习效率η更新参数θ:

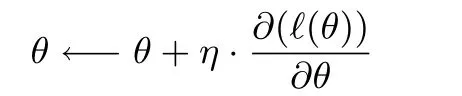
4）使用LBP计算未知社区划分用户的社区标签YU，重新计算f（yi）

直至参数θ 取值收敛

3.4模型推理

接下来，根据学习所得到的参数θ，我们需要推断每个未知社区标签用户的社区标签，所采用的方法就是寻找使目标函数最大化的一个标签配置，即：

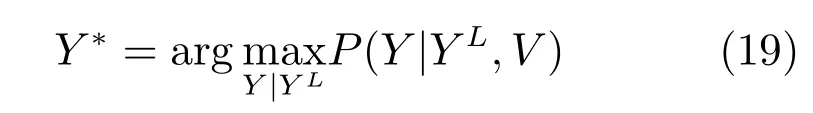
这里我们需要再一次使用LBP算法，通过此算法计算出未知社区标签用户的社区标签.通过计算边缘分布函数P（yi|YL，V），然后取此边缘分布函数取得最大值的变量值，作为未知社区标签用户的社区标签，从而获得社交网络的最终社区划分.

值得注意的是，虽然文章研究的问题的前提是两种先验信息之间不存在冲突，但是我们同时也考虑了更多的情况.对于两种先验信息，如果从一种直接可以推出另一种，或者说两种数据提供的信息是等价的，表明此时存在信息冗余，我们仅仅利用类标签信息；若二者存在冲突，表明此时存在噪声数据，我们忽略所有相冲突的先验信息.此外，分析我们的概率模型中加入的两类先验信息，对于已知的用户社区标签，因为是作为训练的标记数据，最终得到的社区划分一定符合这些信息；但对于必须连接和不能连接约束，通过定义约束势函数，因为是尽量从概率的角度满足约束，因此不能确保最终得到的社区划分一定满足这两类约束条件.通过以上两种方式，确保在我们的方法中，不会出现两种先验信息相互冲突的情况.

4　实验分析

本文从两个方面对提出的半监督社区发现方法进行评价，一个是考虑在具有噪声的网络中，评价本文提出的社区发现方法的鲁棒性，另一个是与其他社区发现方法进行比较，展现本文提出方法的有效性.

4.1数据集

本文选择了3个真实的数据集进行实验，其中包括两个较小的数据集-Zachary社会关系网络和海豚关系网，以及一个大的数据集-DBLP协作网.这3个数据集都拥有清晰的社区结构，能够方便对试验结果进行验证.

Zachary社会关系网是社交网络分析领域中经常被用到的一个小型测试网络.20世纪70年代，Wayne Zachary花了三年时间（1970～1972年）观察美国一所大学空手道俱乐部成员间的社会关系，然后构造了一个俱乐部成员社会关系网（Zachary′s karate club network）.网络中的每个节点代表一个俱乐部成员，如果两个成员经常一起出现在俱乐部活动（如空手道训练、俱乐部聚会等）之外的其他场合，代表在俱乐部之外他们可以被称为朋友，则两个成员之间存在连边，整个网络包含34个节点，78条边.在调查过程中发现，因为俱乐部教练Mr.Hi（v1）与主管John A.（v34）之间的争执，该俱乐部被分裂为了2个各自以他们为核心的小集团.Zachary社会关系网是常用于检验社团发现算法有效性的网络［1，3，9］，该网络真实社团结构如图2所示，图中不同颜色的节点代表分裂后的不同集团的成员.

海豚关系网也是社交网络分析领域中常被使用到的一个真实网络［30］.Lusseau等花了7年的时间，通过对新西兰Doubtful Sound峡湾栖息的一个海豚群体（该群体由2个家族共62只宽吻海豚组成）进行观察，构造了一个海豚关系网.网络中的节点表示一个海豚，边代表两个海豚之间存在频繁的接触，最终的网络包含了62个节点和159条边.其真实社区结构如图3所示，不同家族的海豚成员使用不同的颜色进行区分，较大的海豚家族拥有了42个成员节点，而较小的家族仅仅拥有20个节点.

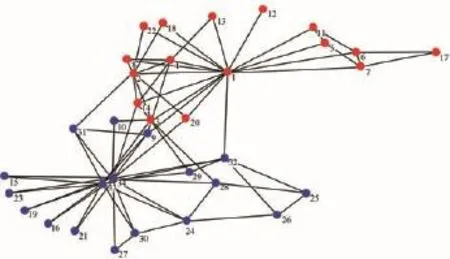
图2　Zachary网络的真实社团结构Fig.2　Community structure of Zachary′s karate club network

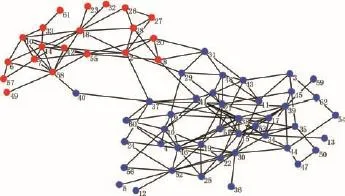
图3　海豚关系网的真实社团结构Fig.3　Community structure of dolphin social network

第三个是DBLP数据集，我们使用Yang等［31］提取的DBLP共同作者关系网络，网络中的两个作者至少合作过一篇文章，则他们之间具有一条连边.整个网络包括317080个节点，1049866条边，平均聚类系数为0.6324.数据集中包含了Ground-truth社区，节点被划为13477个社区.数据能够在斯坦福网络分析平台1被下载.

注意，在3个数据集中，根据已知的社区划分设置我们的模型中期望的社区集合，即将社区个数设置为已知的社区标签的数据.

4.2度量指标

为了度量社区发现的质量，我们选择成对F-measure（Pairwise F-measure）［32］作为度量指标，Basu通过将信息领域中的F-measure引入到半监督聚类中，提出成对F-measure的定义，用来度量半监督聚类算法的质量.本文选择成对F-measure来测试社区发现算法的质量.我们首先给出社区发现中的准确率和召回率的定义：

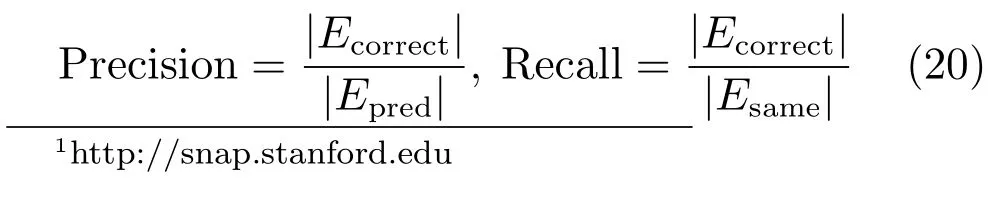
其中，Epred是预测到的社区内的节点对的集合，Esame是真实情况下社区内的节点对的集合，Ecorrect=Epred∩Esame是正确预测的在社区内的节点对的集合，因此我们可以得到成对F-measure的定义：

显然F-measure越大，表示社区发现的预测结果越好.

4.3抗噪声能力评价

大量的工作已经证明［1，3，6，8，30］，在网络数据真实地反映了社交网络中用户之间真实关系的情况下，包括模块度优化方法在内的很多社区发现方法都可以很好地发现网络中的社区结构.但是通常情况下，真实的社交网络中常常包含一些错误的或缺失的用户关系，例如在Twitter和微博中，存在很多广告用户，相比真实用户之间的关注关系，他们对真实用户的关注有很大的区别，甚至可以当作噪声连接；再如，在Facebook中，生活中亲密的朋友可能并未在网络中建立朋友关系，存在缺失的连边，因此并未获得完全的社会关系.在这些情况下，使得我们发现的社区常常难以反映网络的真实社区结构.因此，在本小节中，我们希望在噪声环境下，验证通过融入先验信息到社区发现中是否可以有效地提高预测的精度.

在实验中，首先通过在真实的社交网络中随机地加入和删除用户关系，来增加噪声，然后在各种噪声比例下，通过加入不同程度的用户引导信息，进行半监督的社区发现，进而比较不同情形下社区发现的F-measure值.对于先验信息的融入，我们区分两种情况，分别为仅仅考虑已知部分用户社区标签的情况，以及同时考虑已知部分用户社区标签和增加用户约束的情况.下面我们首先在两个网络中，分别给出在几种情况下进行半监督社区划分的例子.

图4（a）中给出了没有噪声的情况下，Zachary社会关系网络中通过融合5个已知用户（7、13、15、27和28）的社区标签，使用我们的半监督社区发现方法FG-SSCD预测得到的社区划分，得到的F-measure结果为0.9462，有1个节点（10号）产生了误分.图4（b）中是没有噪声的情况下，海豚社会网中通过融合5个已知用户（14、22、31、37和50）的社区标签，我们的半监督社区发现方法预测得到的社区划分，F-measure得到的结果为0.9723，有2个节点（29号和40号）产生了误分.

为了加入噪声数据到网络中，我们随机选择一定比例的节点对，如果它们之间没有连接，我们使其产生连接，如果它们之间存在连接，则删除这个连接.当在 Zachary网络中加入5个噪声数据（增加了5个新的连接（13，14）、（17，31）、（20，25）、（22，34）、（10，26）），加入5个已知类标签（4，5，16，24，26），此外加入5个约束（必须连接约束：（5，17）、（4，22）、（16，29），不能连接约束：（14，33）、（7，25））的情况下，图5（a）中给出了 FG-SSCD 模型获得的社区划分，得到的 F-measure结果为 0.9462，仅仅 1个节点（31号）产生了误分.在海豚社会网中，当加入5个噪声数据（增加了5个新的连接（3，24）、（9，37）、（14，46）、（28，52）、（47，62）），加 入5个 已 知 类 标 签（7，17，44，46，60），此外加入10个约束（必须连接：（34，45）、（24，40）、（20，26）、（3，38）、（48，51）、（8，58）、（9，29），不能连接：（15，55）、（2，25）、（7，50））的情况下，FG-SSCD模型获得的社区划分如图5（b）所示，F-measure为0.9432，有3个节点（40，47，54）产生了误分.

图4　FG-SSCD模型发现的社区结构（无噪声）Fig.4　Community structure from FG-SSCD（without noise）

以上几种情况下，不管有无噪声数据，在两个网络中进行的半监督社区发现，都取得了较高的F-measure值，获得了较好的社区发现结果.为了进一步验证我们的半监督社区发现方法在噪声环境下的有效性，我们选择了两种著名的无监督的社区发现算法进行对比，以验证融入先验信息对于社区发现的影响.

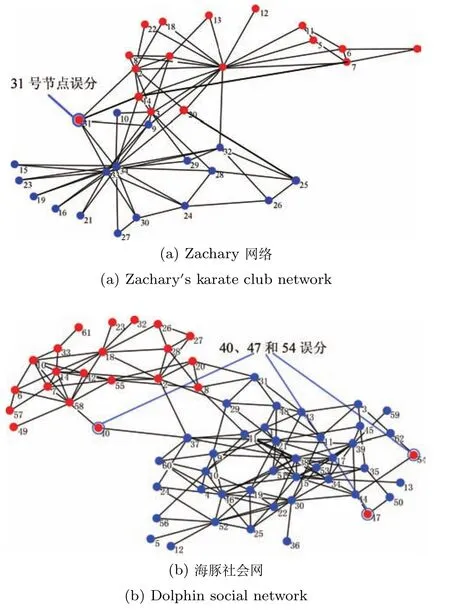
图5　FG-SSCD模型发现的社区结构（有噪声）Fig.5　Community structure from FG-SSCD（with noise）

1）快速Newman算法（Fast-Newman，FN）［8］，FN算法是Newman等提出的一种基于模块度优化的贪婪算法.该算法是在使得模块度不断增加的基础上进行，即每次合并沿着使模块度增多最大和减小最少的方向进行.在Zachary和海豚社会网的实验中，根据实际存在的社区个数，我们将FN算法的社区个数指定为2，而在DBLP中，最终社区个数根据模块度最大值设置.

2）基于信息论的算法（Information-theoretic approach，IT）［33］，这种方法将社区发现过程转化为一个信号通信过程.通过在信息过程中对网络结构信息进行信号编码和解码，信息丢失最少时，编码后得到的社区结构为最优的社区划分.这种方法并没有设定发现社区的个数.

我们将网络中的噪声比例分别设置为2%、4%、6%、8%、10%，由于我们的方法是随机产生噪声和先验信息，因此我们在不同比例的噪声环境下，选择50次的平均结果作为实验的最终结果进行比较.图6中给出了不同噪声比例下，分别执行FN和IT算法，以及融入不同比例的先验信息的情况下通过FG-SSCD模型，得到的社区划分实验对比结果.从图中可以看出，在Zachary和海豚社会网中，IT算法的性能显著低于其他算法，这是因为IT并没有预先设定社区个数.事实上，社区个数也是一种先验信息，这从另一个侧面也反映出先验信息有利于提高社区发现的鲁棒性.三个不同的网络中，在无噪声环境下，我们的方法通过融合先验信息未必能获得比FN算法更好的社区划分.可是在添加噪声数据之后，在不同的噪声比例下，通过我们的方法，融合不同比例的先验信息，都能显著地提高社区发现的精度，而且先验信息越多，得到的预测精度越高.因为现实世界的网络中，通常都包含了大量的噪声，因此通过融入先验信息到社区发现中，能够提高社区发现算法的鲁棒性，发现的社区更能够有效地揭示现实世界的网络中的真实社区结构.

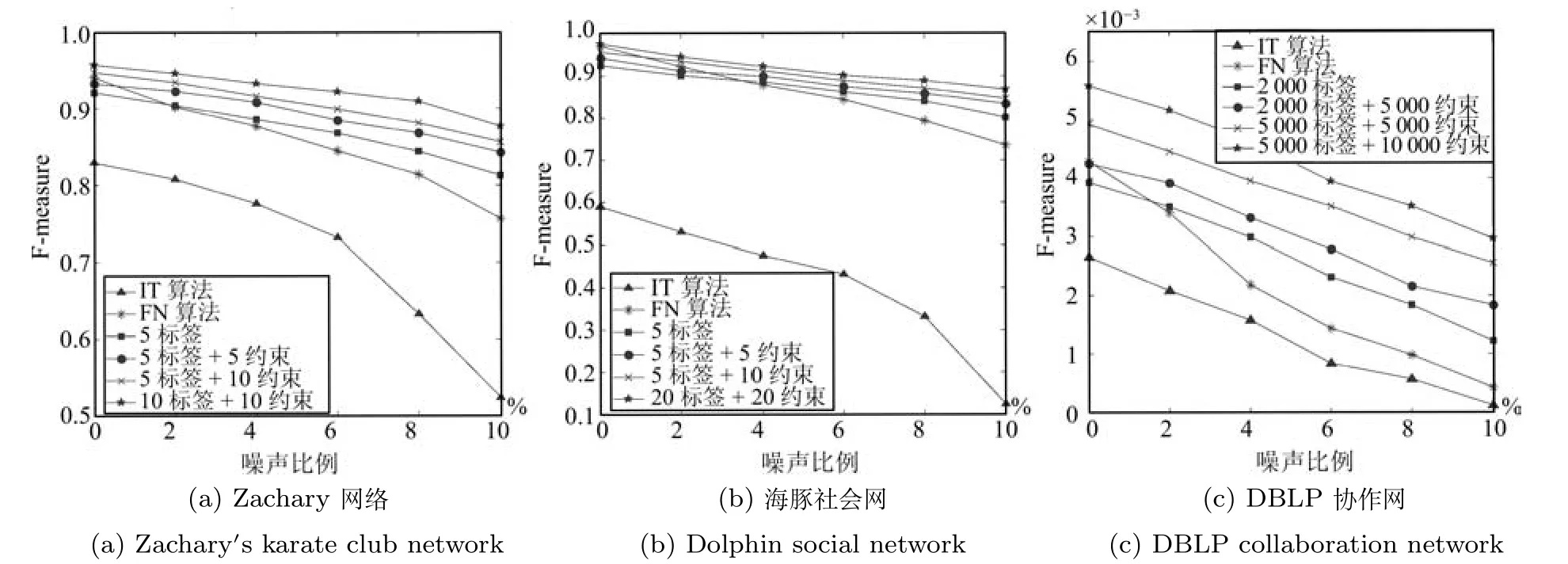
图6　不同噪声比例下的社区发现预测精度对比Fig.6　The prediction accuracy with different noise rate

4.4有效性评价

为了体现我们提出的半监督社区发现算法的有效性，我们选择Eaton等最新提出的半监督的Spin-Glass模型［2］与我们的FG-SSCD模型进行对比，半监督的Spin-Glass模型既可以融入已知的节点社区划分，又可以考虑节点之间的约束，在后面的内容中我们将其简称为Spin-Glass模型.由于在Eaton等的实验中并没有同时考虑两种先验信息，为了与FG-SSCD模型进行对比，在我们的实验中同时将两种信息融入到Spin-Glass模型中，这样可以在考虑了相同的先验信息的情况下将FG-SSCD模型与Spin-Glass模型的社区划分结果进行对比.此外，Spin-Glass模型中的参数设置与文献［2］相同，全部为1.

我们分别在三个网络中，在设置不同的噪声比例的情况下，对每一项实验独立重复50次，然后取F-measure的平均值，图7给出了我们提出的半监督社区发现算法与半监督的Spin-Glass模型的比较结果.从图中可以看出，在网络中有噪声的情况下，不管是Zachary网络还是海豚社会网中，本文的结果一致优于Spin-Glass模型的社区发现结果.三个网络中，本文算法得到的平均F-measure比Spin-Glass模型分别提高了6.34%、16.36%和12.13%.因为两种半监督社区发现方法都融入了相同的先验信息，相比Spin-Glass模型通过用户的经验知识设置参数以确定各类信息的权重，本文方法通过自动优化特征因子函数的权重，可以自动确定各种信息对于社区划分的贡献程度，有助于提高社区划分的精度.

5　结论

本文研究了社区发现这一社交网络分析中长期关注的问题，但当前大部分的研究都聚焦在如何在网络中自动发现社区的问题，在大量具有数据缺失或噪声的网络中，自动社区发现方法往往难以发现网络中的真实社区结构.而通过在社区发现中融合先验信息，进行半监督的社区发现，可以有效地提高社交网络中社区发现的预测精度.在本文中，基于因子图模型，通过融入先验信息到一个统一的概率框架中，本文提出一种半监督的社区发现模型-FGSSCD模型，研究具有用户引导情况下的社交网络社区发现问题.在三个真实的社交网络数据中进行实验，实验表明通过融入先验信息可以有效地提高社区发现的精度.另外，与一种最新的半监督社区方法（半监督的Spin-Glass模型）进行对比，实验结果显示我们的FG-SSCD模型可以实现更好的社区划分.

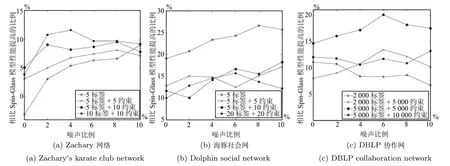
图7　不同噪声比例下，与Spin-Glass模型相比较，FG-SSCD模型F-measure值提高的比例Fig.7　The percent improvement in F-measure of our approach against Spin-Glass model with different noise rate

References

1 Fortunato S.Community detection in graphs.Physics Reports，2010，486（3-5）:75-174

2 Eaton E，Mansbach R.A spin-glass model for semisupervised community detection.In:Proceedings of the 26th AAAI Conference on Artificial Intelligence.Toronto，Ontario，Canada:AAAI，2012:900-906

3 Newman M E J，Girvan M.Finding and evaluating community structure in networks.Physical Review E，2004，69（2）: 026113-1-026113-15

4 Good B H，De Montjoye Y A，Clauset A.Performance of modularity maximization in practical contexts.Physical Review E，2010，81（4）:046106-1-046106-19

5 Yang Z，Tang J，Li J Z，Yang W J.Social community analysis via a factor graph model.IEEE Intelligent Systems，2011，26（3）:58-65

6 Girvan M，Newman M E J.Community structure in social and biological networks.Proceedings of the National Academy of Sciences of the United States of America，2002，99（12）:7821-7826

7 Brandes U，Delling D，Gaertler M，Gorke R，Hoefer M，Nikoloski Z，Wagner D.On modularity clustering.IEEE Transactions on Knowledge and Data Engineering，2008，20（2）:172-188

8 Newman M E J.Fast algorithm for detecting community structure in networks.Physical Review E，2004，69（6）: 066133

9 Duch J，Arenas A.Community detection in complex networks using extremal optimization.Physical Review E，2005，72（2）:027104

11 White S，Smyth P.A spectral clustering approach to finding communities in graph.In:Proceedings of the 2005 International Conference on Data Mining.New York，USA:IEEE，2005，5:76-84

14 Shen H W，Cheng X Q，Fang B X.Covariance，correlation matrix，and the multiscale community structure of networks. Physical Review E，2010，82（1）:016114-1-016114-9

17 Mucha P J，Richardson T，Macon K，Porter M A，Onnela JP.Community structure in time-dependent，multiscale，and multiplex networks.Science，2010，328（5980）:876-878

18 Ma X K，Gao L，Yong X R，Fu L D.Semi-supervised clustering algorithm for community structure detection in complex networks.Physica A:Statistical Mechanics and its Applications，2010，389（1）:187-197

19 Allahverdyan A E，Ver Steeg G，Galstyan A.Community detection with and without prior information.EPL（Europhysics Letters），2010，90（1）:983-995

20 Liu D，Liu X，Wang W J，Bai H Y.Semi-supervised community detection based on discrete potential theory.Physica A:Statistical Mechanics and its Applications，2014，416: 173-182

21 Li L，Du M，Liu G F，Hu X G，Wu G Q.Extremal optimization-based semi-supervised algorithm with conflict pairwise constraints for community detection.In:Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining.New York，USA:IEEE，2014.180-187

22 Yang L，Cao X C，Jin D，Wang X，Meng D.A unified semi-supervised community detection framework using latent space graph regularization.IEEE Transactions on Cybernetics，2014，45（11）:2585-2598

23 Yang L，Jin D，Wang X，Cao X C.Active link selection for efficient semi-supervised community detection.Scientific Reports，2015，5:9039-1-9039-12

24 Tang W B，Zhuang H L，Tang J.Learning to infer social ties in large networks.Machine Learning and Knowledge Discovery in Databases.Berlin Heidelberg:Springer，2011，6913: 381-397

25 Hammersley J M，Clifford P.Markov fields on finite graphs and lattices.1971.

26 Geman S，Geman D.Stochastic relaxation，Gibbs distributions，and the Bayesian restoration of images.IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6（6）:721-741

27 Basu S，Bilenko M，Mooney R J.A probabilistic framework for semi-supervised clustering.In:Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York，USA:ACM，2004.59-68

29 Murphy K P，Weiss Y，Jordan M I.Loopy belief propagation for approximate inference:an empirical study.In:Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence.San Francisco，CA，USA:Morgan Kaufmann Publishers Inc.，1999.467-475

30 Lusseau D，Schneider K，Boisseau O J，Haase P，Slooten E，Dawson S M.The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations.Behavioral Ecology and Sociobiology，2003，54（4）: 396-405

31 Yang J，Leskovec J.Defining and evaluating network communities based on ground-truth.Knowledge and Information Systems，2015，42（1）:181-213

32 Basu S.Semi-supervised Clustering:Probabilistic Models，Algorithms and Experiments［Ph.D.dissertation］，University of Texas at Austin，USA，2005.

33 Rosvall M，Bergstrom C T.An information-theoretic framework for resolving community structure in complex networks.Proceedings of the National Academy of Sciences of the United States of America，2007，104（18）:7327-7331

黄立威北京市遥感信息研究所工程师. 2014年获得解放军理工大学指挥信息系统学院博士学位.主要研究方向为数据挖掘和机器学习.本文通信作者.

E-mail:dr_huanglw@163.com

（HUANG Li-WeiEngineer at Beijing Institute of Remote Sensing.He received his Ph.D.degree in computer science from PLA University of Science and Technology in 2014.His research interest covers data mining and machine learning.Corresponding author of this paper.）

李彩萍北京市遥感信息研究所高级工程师.2015年获得装备学院博士学位.主要研究方向为系统仿真.

E-mail:alninglcp@sina.com

（LI Cai-PingSenior engineer at Beijing Institute of Remote Sensing. She received her Ph.D.degree from PLA Institute of Equipment in 2015. Her main research interest is system simulation.）

张海粟中国人民解放军国防信息学院副教授.2012年获得解放军理工大学博士学位.主要研究方向为数据挖掘.

E-mail:zhanghaisu@139.com

（ZHANG Hai-SuAssociate professor at the Institute of National Defense Information.He received his Ph.D. degree in computer science from PLA University of Science and Technology in 2012.His main research interest is data mining.）

刘玉超中国指挥与控制学会副秘书长. 2012年获得清华大学计算机科学与技术系博士学位.主要研究方向为数据挖掘和机器学习.

E-mail:yuchao_liu@163.com

（LIU Yu-ChaoDeputy secretarygeneral at Chinese Institute of Command and Control.He received his Ph.D.degree from the Department of Computer Science and Technology，Tsinghua University in 2012.His research interest covers data mining and machine learning.）

李德毅中国电子系统工程研究所研究员.中国工程院院士.国际欧亚科学院院士.1983年获得英国爱丁堡Heriot-Watt大学博士学位.主要研究方向为人工智能.E-mail:lidy@cae.cn

（LI De-YiProfessor at the Institute of Electronic System Engineering.He is currently an academician of Chinese Academy of Engineering，a member of the International Eurosian Academy of Science.He received his Ph.D.degree in computer science from Heriot-Watt University in Edinburgh，UK.His main research interest is artificial intelligence.）

刘艳博北京市遥感信息研究所工程师. 2013年获得国防科技大学硕士学位.主要研究方向为遥感信息应用.

E-mail:liuyanbonudt@163.com

（LIU Yan-BoEngineer at Beijing Institute of Remote Sensing.She received her master degree in automation from National University of Defense Technology.Her main research interest is remote sensing information application.）

A Semi-supervised Community Detection Method Based on Factor Graph Model

HUANG Li-Wei1LI Cai-Ping1ZHANG Hai-Su2LIU Yu-Chao3LI De-Yi4LIU Yan-Bo1

Community detection is an important research direction of social network analysis.Most of the current studies focused on automated community detection.However，in networks having missing data or noise，the ability for an automated community detection algorithm to discover true community structures may degrade rapidly with the increase of noise.On the other hand，semi-supervised community detection provides a feasible way for solving the above problem by incorporating priori information into the community detection process.In this paper，based on the factor graph model，by incorporating the priori information into a unified probabilistic framework，we propose a factor graph-based semisupervised community detection method.We evaluate the method with three different genres of real datasets（Zachary，Dolphins and DBLP）.Experiments indicate that incorporating priori information into the community detection process can improve the prediction accuracy significantly.Compared with a latest semi-supervised community detection algorithm（semi-supervised spin-glass model），the F-measure of our method is on average improved by 6.34%，16.36%and 12.13% in the three datasets.

Social networks，semi-supervised community detection，factor graph，social networks analysis，probability reasoning

Manuscript May 5，2015；accepted January 19，2016

10.16383/j.aas.2016.c150261

Huang Li-Wei，Li Cai-Ping，Zhang Hai-Su，Liu Yu-Chao，Li De-Yi，Liu Yan-Bo.A semi-supervised community detection method based on factor graph model.Acta Automatica Sinica，2016，42（10）:1520-1531

2015-05-05录用日期2016-01-19

国家重点基础研究发展计划（973计划）（2014CB340401），国家自然科学基金（61035004，61273213，61305055）资助

Supported by National Basic Research Program of China（973 Program）（2014CB340401），National Natural Science Foundation of China（61035004，61273213，61305055）

本文责任编委周志华

Recommended by Associate Editor ZHOU Zhi-Hua

1.北京市遥感信息研究所北京1008542.中国人民解放军国防信息学院武汉4300103.中国指挥与控制学会北京1000484.中国电子系统工程研究所北京100039

1.Beijing Institute of Remote Sensing，Beijing 100854 2.Institute of National Defense Information，Wuhan 430010 3.Chinese Institute of Command and Control，Beijing 100048 4.Institute of Electronic System Engineering，Beijing 100039