轨姿控推进系统用电磁阀性能仿真研究

杨亦婷，李进贤，张博斌

（1.西安航天信息研究所，陕西西安710025；2.西北工业大学航天学院，陕西西安710072；3.航天动力技术研究院，陕西西安710025）

轨姿控推进系统用电磁阀性能仿真研究

杨亦婷1，李进贤2，张博斌3

（1.西安航天信息研究所，陕西西安710025；2.西北工业大学航天学院，陕西西安710072；3.航天动力技术研究院，陕西西安710025）

轨姿控推进系统采用电磁阀控制内部流体通路的开启与断流，从而实现其重复启动和脉冲工作。在轨姿控推进系统快速稳定工作问题的研究中，电磁阀的性能对推进系统至关重要。针对轨姿控推进系统用电磁阀，基于电磁学及运动学等基本原理，建立了电磁阀动态数学模型，利用Matlab Simulink软件进行了动态仿真，得到了电磁阀动态响应特性；采用CFD软件对阀门内部流场进行数值模拟仿真，获得了精确的静态流阻特性，直观展现了电磁阀动态流场，为电磁阀的性能优化和轨姿控推进系统的性能提高提供依据。

轨姿控推进系统；电磁阀；仿真

0　引言

轨姿控推进系统广泛应用于各类航天器和导弹武器，其主要作用是为航天器飞行过程中变轨和姿态控制提供控制力和控制力矩［1］。在液体轨姿控推进系统中，为了保证发动机的正常启动和关机、稳态工作时的工作稳定性和再次工作的重复性，要求电磁阀的工作性能具有足够的快速性、稳定性和重复性。

对电磁阀进行动态特性研究时，准确建立电磁阀的数学模型是难点。本文采用磁路分析法建立了所研究电磁阀的动态数学模型，在建立运动方程时，除了考虑摩擦力、液压力等阻力外，还研究了电磁阀在运动过程中受到的稳态及瞬态液动力，真实还原了电磁阀的受力状态，建立了较为准确的数学模型，并利用Matlab Simulink软件进行了动态仿真研究，得到了电磁阀的动态响应特性；采用CFD软件对阀门内部流场进行数值模拟仿真，获得了精确的静态流阻特性，直观地展现了电磁阀的运动状态，给出了电磁阀在运动过程中内部流场压力的变化情况，并对结果进行了分析研究。

1　电磁阀工作原理

应用在液体轨姿控推进系统中的电磁阀一般为螺管式电磁阀［2］，主要由阀体、阀芯、线圈、圆柱弹簧以及蝶形弹簧等组成，其结构简图如图1。

图1　螺管式电磁阀结构简图Fig.1　Structural sketch of solenoid valve

当电磁阀通电后，挡铁和阀芯之间产生电磁吸力，阀芯在电磁吸力作用下克服阀芯上的各种阻力，使阀芯向左运动，电磁阀打开。当发出关机指令时，电磁阀断电，电磁吸力消失，阀芯在弹簧力和液压不平衡力的作用下克服剩磁吸力以及摩擦阻力向右运动，切断阀芯与阀座之间的通路，电磁阀关闭。

2　电磁阀动态过程建模与仿真

2.1电磁阀数学模型的建立

电磁阀的工作过程涉及到电力、磁力、机械力及液力的耦合作用，其数学模型由电路方程、磁路方程和运动方程组成［3-5］。为准确建立电磁阀的数学模型，在运动方程中考虑稳瞬态液动力的影响，真实还原电磁阀的受力状况。

2.1.1电路方程

根据电磁感应定律，有

根据电压平衡定律，有

式中：e为感应电动势；N为线圈匝数；Φ为通过线圈中的磁通量；U为控制电压；R为线圈电阻。

2.1.2磁路方程

由于铁芯和阀芯材料的磁导率远大于空气的磁导率，铁芯和阀芯的磁阻远小于气隙磁阻，因此磁路的总磁阻可近似为气隙磁阻。根据基尔霍夫磁压定律，可得出磁路计算的数学模型，即

式中Rδ为磁力线经过气隙的磁阻。气隙磁阻为

式中：gmax为初始气隙长度；x为阀芯位移；μ0为真空中的磁导率；S为有效气隙面积。

根据麦克斯韦电磁吸力公式，电磁阀的电磁吸力公式为

2.1.3运动方程

电磁阀阀芯部分在工作过程中受到电磁力、弹簧力、摩擦力、液动力和液体压力的共同作用，则根据牛顿第二定律，电磁阀的运动方程为

式中：m为电磁阀运动部件的质量；BV为黏性摩擦系数；Bf为瞬态液动力阻尼系数；Fso为弹簧的预紧力；K为弹簧刚度；Kf为稳态液动力刚度；Fp为液体压力。

对于液体压力，有

式中：p1为入口压强；p2为出口压强；S1为入口面积；S2为出口面积。

对于出口压强，可由通过阀口的流量求得，即

式中：q为电磁阀体积流量；Cd为流量系数；d为出口流通直径；ρ为流体密度。

2.2电磁阀动态特性仿真

电磁阀是一个典型的动态非线性系统，在其工作过程中，电路系统、磁路系统和机械系统都在快速发生变化。采用Simulink能快速、准确地创建该电磁阀动态系统的计算机模型，进行仿真计算［6］。根据电磁阀电路、磁路及运动方程，建立的电磁阀整体仿真模型如图2所示。本文所研究电磁阀的技术参数见表1。

图2　电磁阀仿真模型Fig.2　Simulation model of solenoid valve

表1　电磁阀技术参数Tab.1　Technical parameters of solenoid valve

针对表1所列参数，对电磁阀开启和关闭过程进行仿真计算，输入电压为28 V，作用时间为0.2 s，仿真时间为0.3 s，计算得出电磁阀动态响应特性曲线如图3所示。图中分别给出了电流、电磁吸力及阀芯位移随时间变化的曲线。

如图3所示，电磁阀从线圈通电到最后阀芯达到闭合位置的过程称为电磁阀的开启过程。该过程可分为吸合触动过程和吸合运动过程［3］。由于电磁铁是一个带铁心的线圈，它具有一定的电感值。当线圈加上电压后，线圈的电流从零开始上升，磁通Φ也随着增加。磁通的增长在线圈中要产生感应电势，它总是阻止电流的增长，因此电流不可能跃变至稳定值，而是按指数曲线的规律逐渐增长直至稳定值。随着电流的增长，阀芯的吸力也逐渐增加，当吸力大于反力后，阀芯开始运动，此时对应的电流称为吸合触动电流。电流由零上升到吸合触动电流所需的时间称为吸合触动时间t1。这段过程如图3（a）中所示的OA段，即为吸合触动过程。

图3　电磁阀响应特性曲线Fig.3　Dynamic response characteristics of solenoid valve

由于阀芯运动引起电感变化，因而产生反电势，这个反电势是阻止电流上升的，故阀芯运动开始时电流不但不继续上升，反而逐渐下降。阀芯运动速度越快，产生的反电势也越大，电流下降也越快。从阀芯开始运动到最后达到闭合位置所需的时间称为吸合运动时间t2。这段过程如图3（a）中所示的AB段，即为吸合运动过程。吸合触动时间与吸合运动时间之和称为吸合时间，即为电磁阀的开启响应时间T1。由仿真结果知，该型电磁阀的开启响应时间为0.034 s。阀芯运动终了后，线圈电流继续按指数曲线上升至额定值。

电磁阀从线圈断电到阀芯回到原始位置的过程称为关闭过程，与开启过程类似，可分为释放触动过程和释放运动过程，两个过程所用时间之和即为电磁阀的关闭响应时间T2。由仿真结果知，电磁阀的关闭响应时间为0.036 s。

通过将该仿真模型计算所得的响应特性与同类型电磁阀动态特性［7］对比可知，该计算结果与同类电磁阀响应特性一致，所建模型精确可行。

3　电磁阀内部流场建模与仿真

3.1内部流场几何模型的建立

根据所研究电磁阀的基本结构，流体在电磁阀内的流动过程为：电磁阀通电打开后，流体先从入口流入阀腔，之后从阀腔端部六个均布的斜60度的圆孔流出阀腔，随后流向出口。因此，可根据流体的流动过程建立电磁阀内部流场的三维模型。在理解电磁阀内部流体流动的基础上，通过Solidworks软件建立电磁阀内部流场的几何模型，如图4所示。流体流入圆柱型阀腔后，经由6个均布的流通孔后流出阀腔，之后流向出口。

图4　电磁阀内流场Solidworks模型Fig.4　Solidworks model of flow field in solenoid valve

3.2静态流场数值计算与结果分析

3.2.1计算初始条件

对于本电磁阀，完全开启状态的阀芯开度为0.4 mm，在计算过程中，保持入口质量流率为45.5 g/s不变。选用肼作为流体介质，通过改变电磁阀的阀芯开度，得到阀门在不同状态下的流动参数，从而拟合出其静态流阻特性。阀门入口及出口的直径均为2.5 mm，入口压强为2.2 MPa。

3.2.2计算结果与分析

表2列出了由数值计算得出的在阀门开度从0.05 mm到0.4 mm变化时，对应的阀门出入口的压降值，并以表中数据为基础进行分析研究。

表2　阀芯开度与对应压降值Tab.2　Valve core opening versus pressure drop value

由表2可以看出，随着阀芯开度的增加，阀门出入口压降是增大的，且在阀门开度较小时，压降随阀芯开度增加的增大幅度较明显。

由流体力学可知，通过阀口的流量公式为：

式中：qv为通过阀门的体积流量，可通过qv=m./ρ求得；Cd为流量系数；Av为阀门有效流通面积；d为阀门流通直径；x为阀芯开度；Δp为阀门出入口压差；ρ为流体密度。

由上述流量公式以及表2中列出数据可计算得出在不同阀芯开度下，流量系数Cd与阀芯开度x之间的对应关系。将计算所得的数据进行拟合得出流量系数Cd与阀芯开度x的数学关系式如下：

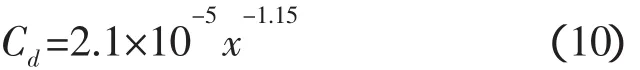
该公式给出了该螺管式电磁阀的静态流阻特性。

3.3动态流场数值计算与结果分析

3.3.1计算初始条件

设置电磁阀初始阀芯开度为0.05 mm，选择肼作为阀腔内流体介质，入口质量流量为45.5 g/s，入口压力为2.2 MPa，阀芯质量为0.0123 kg，阀门入口及出口的直径均为2.5 mm。阀芯在耦合力作用下使阀门开启，时间步长为0.000 1 s，总位移为0.35 mm，直至电磁阀完全打开，仿真结束。计算网格由Fluent软件的前处理器Gambit来生成，采用结构化网格与非结构化网格相结合的划分方式。网格更新方法采用动网格技术中的弹性光顺法和局部网格重划法［8］，使用UDF文件对阀芯运动方式进行定义［9］。

3.3.2计算结果与分析

由数值模拟可以得到电磁阀在开启过程中内部流场压力与速度随时间的变化情况。图5所示为电磁阀运动过程中内部流场分别在0 ms，15 ms以及30 ms时的压力云图。

图5　t=0 ms，15 ms，30 ms内流场的压力云图Fig.5　Pressure nephogram of internal flow field at t=0 ms，15 ms，30 ms

从内流场压力云图可以看出，电磁阀流场分布关于z轴对称，同时随着电磁阀的打开，入口压强开始减小，而出口压强则较为平稳。内流场中存在明显的高压区和低压区。在0 ms时，高压区压力最高可达到1.22 MPa，低压区压力约为1 MPa，之后随着电磁阀阀芯开度的增大，高压区压力逐渐减小，且流体从阀芯打开的缝隙流向出口的过程中，会在出口处形成一个压强漩涡，且漩涡内部压强较高，约为1.16 MPa，而外缘区域压强较低，约为1.08 MPa，并且随着电磁阀阀芯开度的增大，该区域范围会逐渐扩大。同时，随着电磁阀的打开，流体从六个圆孔流出阀腔时，在阀腔底端会逐渐形成了一个压强局部最大区域。

4　结论

考虑轨姿控推进系统用电磁阀在运动过程中受到的稳瞬态液动力，建立了准确的电磁阀数学模型，通过Matlab Simulink软件进行仿真计算，分析得到了电流、电磁吸力、阀芯位移等可表征电磁阀动态特性的参数的变化规律；采用CFD软件对阀门内部流场进行数值模拟仿真，获得了精确的静态流阻特性，给出了电磁阀在运动过程中内部流场压力的变化情况，进一步了解了电磁阀内部的流动状态，有助于对电磁阀进行优化设计，使其动态响应特性尽量达到最优状态，从而提高整个轨姿控推进系统的工作性能。

［1］OWEN David.Apollo spacecraft propulsion systems designphilosophies，AIAA2010-8813［R］.USA：AIAA，2010.

［2］朱宁昌，刘国球.液体火箭发动机设计［M］.北京：中国宇航出版社，2009.

［3］杨玉涛，张小栋.高速电磁阀模型建立及响应特性研究［J］.测控技术，2008，27（6）.

［4］刘忠，刘卫萍，何谦.高速开关电磁阀动态响应建模与仿真［J］.湖南师范大学自然科学学报，2009，32（3）：53-57.

［5］蔡伟，郑贤林，张志利，等.液压电磁阀故障机理分析与瞬态特性仿真 ［J］.仪器仪表学报，2011，32（12）：2726-2733.

［6］郭立君.柴油机高压共轨燃油系统仿真研究与优化［D］.哈尔滨工程大学，2012.

［7］戴佳，黄敏超，余勇，等.电磁阀动态响应特性仿真研究［J］.火箭推进，2007，33（1）：40-48. DAI Jia，HUANG Minchao，YU Yong，et al.Simulation on the dynamic response characteristics of solenoid valve［J］.Journal of rocket propulsion，2007，33（1）：40-48.

［8］江帆，黄鹏.Fluent高级应用与实例分析［M］.北京：清华大学出版社，2008.

［9］郑丽.大流量减压器的特性研究及内部流场动态仿真［D］.国防科学技术大学，2007.

［10］李荣，冯永保，刘杰，等.基于Fluent的电磁阀内部流场的三维仿真与分析［J］.液压与气动，2013（10）：96-98.

（编辑：王建喜）

Simulation research on performance of solenoid valve for orbit and attitude control propulsion system

YANG Yiting1，LI Jinxian2，ZHANG Bobin3
（1.Xi'an Institute of Aerospace Information，Xi'an 710025，China；2.College of Astronautics，Northwestern Polytechnical University，Xi'an 710072，China 3.Academy of Aerospace Solid Propulsion Technology，Xi'an 710025，China）

In the orbit and attitude control propulsion system，the solenoid valve controls the opening and closing of the fluid passage to achieve the goal of repeated start and pulse operation.It is essential to research the dynamic characteristic ofthe solenoid valve in the stabilityresearch of the orbit and attitude control propulsion system.The dynamic mathematical model of the solenoid valve was established based on fundamental principles ofelectromagnetism and kinematics.The simulation of the dynamic process was conducted by means of Matlab Simulink，by which the dynamic characteristics of the solenoid valve were obtained.CFD was used in the numerical simulation of the flow field in the solenoid valve and the accurate static flow resistance was acquired，which showed the movement state of the solenoid valve visually，and provided a theoretical reference for performance optimization of the solenoid valve and performance improvement of the orbit and attitude control propulsion system.

orbit and attitude control propulsion system；solenoid valve；simulation

V434-34

A

1672-9374（2016）02-0019-06

2015-12-10；

2016-02-25

杨亦婷（1990—），女，硕士研究生，研究领域为火箭发动机情报研究