基于分型转折点的证券时间序列分段表示法
2016-11-10彭佳星肖基毅
彭佳星 肖基毅
基于分型转折点的证券时间序列分段表示法
彭佳星1,2,3肖基毅1
证券时间序列是证券交易价格的一组观测数据,是一种有其自身显著的特点的时间序列,针对这些特点我们提出一种基于分形理论与K线图形特点的分段方法,经过理论分析与实践证明其划分的证券时间序列分段有其合理性。在对时间序列数据压缩率很高的情况下,还能保持较好的拟合误差,并能较好地描述证券时间序列的走势特征。
分型;转折点;证券时间序列
一、引言
证券时间序列是按证券交易时间先后排列的一系列证券交易价格观测数据,其观测值按固定的时间间隔采样。证券时间序列属于金融时间序列的一种,因为证券交易金额大交易频率高而受研究者大量关注。
面对海量、高维的证券数据,直接在原始数据上处理难度很大,因此,需要研究合适的数据表示形式,以规约简化数据。目前常见的时间序列特征表示形式有域变化表示法、符号表示法、奇异值分解法、分段聚合近似表示方法(piecewise aggregate approximation,PAA)和分段直线表示法(Piecewise Linear Representation,PLR)等[1]。由于域变换表示法大多基于点距离,无法刻画时间序列的重要特征—动态属性;符号表示法更适应在文本数据挖掘和生物信息等领域中得到较多应用;奇异值分解法时间复杂度高,且从数据集中任意增加或删除一条记录,都要重新运算,不适合证券时间序列数据的动态增加;分段聚合近似表示方法根据是通过对时间序列进行平均分割并利用分段序列的均值来表示原时间序列的方法,极大值、极小值、形态特征等数据容易丢失,不利于体现证券时间序列的趋势特征[2-3]。
PLR算法有不少应用于证券时间序列的实验,一类如詹艳艳等基于斜率的分段法,根据斜率的变化把证券时间序列分成多个序列[4]。这类方法用于证券时间序列分段有一个显著的缺点,同一趋势段会因为涨跌幅度变化较大的而分为多个段,不利于趋势的理解。另一类是以Pratt为代表的重要点分段法,根据序列中反趋势的幅度,用序列分段中的上涨趋势中的最大值或下跌趋势的最小值,与反趋势中某个值的比率小于某个临界值R来判断是否构成反趋势段,从而达到分段的目的[5];以及田野等的改进的重要点分段法,这类方法比基于斜率的分段法能更好的描述证券时间序列的走势特征[6]。
二、问题描述及分型转折点的定义
(一)问题的定义
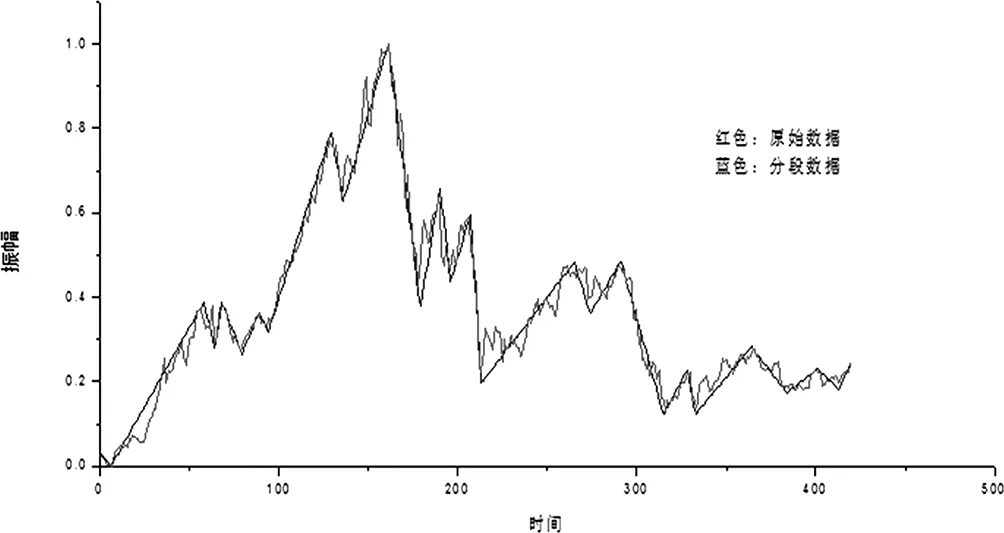
定义1(证券时间序列)证券时间序列是证券交易记录值和交易时间组成的有序集合。记为X= 定义2(时间序列的模式表示)假设证券时间序列是X= X(t)=f(w)+e(t) (2.1) 其中,w是证券时间序列的模式,f(w)是证券时间序列的模式表示,e(t)是证券时间序列与它的模式表示之间的误差。 定义3(证券时间序列的分段线性表示)假设证券时间序列是X= (2.2) 分段方法的目标是对证券时间序列进行降维,减少序列中点的个数的同时保留时间序列数据关键特征,分段直线表示法的重点就在于分段点的选取。 (二)证券时间序列的分形特征与分段评价标准 分形(Fractal)的概念是美籍数学家本华·曼德博首先提出的。以海岸线为例,作为曲线,其特征是极不规则、极不光滑的,呈现极其蜿蜒复杂的变化。我们不能从形状和结构上区分这部分海岸与那部分海岸有什么本质的不同。这种几乎同样程度的不规则性和复杂性,说明海岸线在形貌上是自相似的,也就是局部形态和整体态的相似。 证券交易时间序列数据也具有这样的自相似性,我们从证券交易的日K线图上看到的图形概貌,与从月K线图、日K线、30分钟K线图上看到的图形几乎有同样程度的不规则性和复杂性。国内一些研究也表明,中国股票市场也具有分形特征[7]。这个特征表明证券时间序列中局部与整体之间有一些相似的结构特性,如果这种结构特征能在特征表示法中体现出来,对于证券数据挖掘是很有利的。 目前大多数时间序列特征表示法,追求拟合误差e(t)的最小化。然而证券时间序列特征表示法中,对趋势特征的保留程度,也是衡量特征表示优劣的指标。本文中把拟合误差和趋势特征的保留程度一起作为参照指标。 根据证券数据分形特征的自相似性,以及证券K线图形的拓扑结构,本文提出一种证券数据新型分段方法,命名为分型转折点分段法。 分段思路:根据证券时间序列的拓扑结构特点,所有的转折点必然存在视觉上的高低点,这些高低点可以构成各个趋势段的顶和底。顶和底的出现在图形上会有一定的条件限制,找出序列所有顶和底,就可以确定分段点。这样的分段适合月线、日线、分钟线等各个时间度量单位的证券时间序列。 (一)基本定义 分型转折点分段线性表示法建立在时间序列图形分析的基础之上。 证券时间序列描述的是股票等有价证券的交易价格观测值,记录股票交易在等长时间间隔内的价格数据,常见时间间隔大小为:年、季、月、周、日、60分钟、30分钟、15分钟、5分钟、1分钟。根据分形理论,不同时间间隔的观测值拓扑图形都有一定的自相似特点,通过观测的视觉经验也能看出证券时间序列的自相似性。 本文重点关注某一个时间间隔内观测值的最高价和最低价,用K(i)top表示时间序列第i个观测值的最高价,用K(i)botton表示时间序列第i个观测值的最低价。观测值的图形表示可以用最高价到最低价的垂直连线表示,并命名为K线(也是对证券理论中K线的一种简化)。 (二)两个观测值的组合关系 1、非包含。一根K线的高点比另一根高(低),低点也比另一根高(低),则说这两根K线是非包含的。 定义一:如果K(i+1)top>K(i)top and K(i+1)bottom>K(i)bottom,或者K(i+1)top 2、包含。前一根K线的高低点在后一根K线的高低点范围之内,或者后一根K线的高低点在前一根K线的高低点范围之内,则说这两根K线存在包含关系。 定义二:如果K(i)top>=K(i+1)top and K(i)bottom<=K(i+1)bottom,则说K(i)包含K(i+1);如果K(i)top<=K(i+1)top and K(i)bottom>=K(i+1)bottom,则说K(i+1)包含K(i)。这两种情况都构成包含关系。 (三)证券时间序列的方向(2个非包含关系的观测值决定了方向) 非包含关系的2根K线后一根的高点比前一根高,低点也比前一根高,称为向上(上涨)。非包含关系的2根K线后一根的高点比前一根低,低点也比前一根低,称为向下(下跌)。 定义三:当2个观测值为非包含关系时,如果K(i)top 定义四:当2个观测值为非包含关系时,如果K(i)top>K(i+1)top and K(i)bottom>K(i+1)bottom,则序列的方向是向下(下跌)的。 (四)合并存在包含关系的观测值 1、当序列方向是向上时(存在包含关系的2根K线之前的K线的方向,可以是经过包含关系处理的),以2根K线中的高点的较高者为高点,以2根K线中低点的较高者为低点,合并为1根K线。 2、当K线方向是向下时,以2根K线中的高点的较低者为高点,以2根K线中低点的较低者为低点,合并为1根K线。 定理一:对存在包含关系K线合并时,如果前面序列是向上的,K(合)top=Max(K(i)top,K(i+1)top),K(合)bottom=Max(K(i)bottom,K(i+1)bottom);如果前面序列式向下的,K(合)top=Min(K(i)top,K(i+1)top),K(合)bottom=Min(K(i)bottom,K(i+1)bottom)。 (五)3根K线组合关系(包含关系已作合并处理) 时间序列中存在包含关系的K线做了合并处理之后,3根K线的组合关系只可能是以下四种情况: 顶分型:第二根K线的高点是3根K线高点中最高的,低点是3根K线低点中最高的。 底分型:第二K线低点是相邻三K线低点中最低的,而高点也是相邻三K线高点中最低的。 顶分型的最高点叫该分型的顶,底分型的最低点叫该分型的底。 上升K线:三根K线的高点依次升高,低点依次升高。 下降K线:三根K线的高点依次降低,低点依次降低。 (六)K线的分型 所有的时间序列转折点都必定是顶分型或者底分型(包含关系已经合并),顶、底分型是时间序列走势发生转折的必要非充分条件。 顶分型:第二根K线的高点是3根K线高点中最高的,低点是3根K线低点中最高的。 底分型:第二K线低点是相邻三K线低点中最低的,而高点也是相邻三K线高点中最低的。 顶分型的最高点叫该分型的顶,底分型的最低点叫该分型的底。 (七)分型转折点分段方法 转折点一定有顶分型或者底分型,但顶、底分型要构成转折点需要在视觉上形成一定的转折效果,对数据压缩有帮助,这里引入时间窗的方法,要求顶、底之间满足:顶、底之间不少于N根K线(不包括顶、底所在的K线)。N值越小,分段点越多,压缩率越高;反之,N值越大,分段点越少,压缩率越低。由于趋势的存在,N取值对分段点的影响并不是很大。 由分型到分段确认的几种情况: 先由前两根K线定方向,向上则第一根为底,向下则第一根为顶。包含则再根据下一根K线确定方向。 如果先出顶分型,接下来,如果再出一顶分型则:顶+顶取其中高者为顶;如果一样高,则前者为顶。此时顶仍未确定。等待下一个分型。 如果再出一底分型则:顶+底,1、符合分段要求则为1段,先保存下来。顶已经确定,等待底的确定。2、不符合,则前顶仍未确定。等待下一个分型。 反之,先出底分型,接下来,如果再出一底分型则:底+底取其中低者为底;如果一样高,则前者为底。此时底仍未确定。等待下一个分型。 如果再出一顶分型则:底+顶,1、符合分段定义则为1段,先保存下来。底已经确定,等待顶的确定。2、不符合,此时底仍未确定。等待下一个分型。 3、第一个K线如果不在第一个分型中,则该K线与第一个分型构成一个分段;最后一个分型与最后一个K线构成未定分段。 (一)实验数据 本文中的实验数据来自同花顺方正证券泉友通交易软件。 数据源:选取上证指数420个(2014.10.20-2016.7.5)交易日观测值,包括最高价和最低价,形式为K= (二)实验方法 本文通过使用基于K线分型转折点算法分段,输入为同花顺交易软件导出的股票日K线数据,输出为各个分段点价格和时间。 基于K线分型转折点算法流程如下: 图1 分型转折点算法流程图 (三)实验结果 实验股票时间序列420个,分型转折点分段算法参数N取值5时(即顶底之间不少于5根K线),数据压缩率为94%,拟合误差为0.629。可以直观地看出,压缩后的序列很好地保留了序列总体的走势,如图2 图2 分型转折点分段与原始数据比较 本文针对证券时间序列分段方法提出了一种新的思路,这种分段方法基于证券时间序列本身的特征构造分型,根据分型特征构造分段。实验表明,该分段方法压缩比率很高时,还能很好的保留原是序列的走势结构,是一种很好的分段方法。(作者单位:1.南华大学计算机科学与技术学院;2.衡阳师范学院计算机科学与技术学院;3.智能信息处理与应用湖南省重点实验室) [1]李海林,郭崇慧.时间序列数据挖掘中特征表示与相似性度量研究综述[J].计算机应用研究,2013年5月,1285-1291. [2]Keogh,E,Chakrabarti,K,Pazzani,M,Mehrotra,S.Dimensionality reduction for fast similarity search inlarge time series databases.Knowledge and informationSystems[J],2001,3(3),263-286 [3]Keogh,E.A fast and robust method for pattern matching in time series databases,Proceedings of 9th International Conference on Tools with Artificial Intelligence[C],1997,578-584. [4]詹艳艳,徐荣聪,陈晓云.基于斜率提取边缘点的时间序列分段线性表示方法[J].计算机科学,2006,139-142. [5]Pratt,K.B,Fink,E.Search for patterns in compressed time series.International Journal of Image and Graphics[J],2002,2(1),89-106. [6]田野.改进的基于重要点的时间序列数据分段方法.微型电脑应用[J],2012,48-51. 彭佳星(1974-),男,湖南衡阳人,研究方向:数据挖掘。 肖基毅(1962-),男,湖南新田人,教授,硕士生导师,研究方向:数据挖掘与智能信息系统。
三、分型转折点分段方法
四、实验结果及分析


五、结论
