三相逆变器的结构能控性分析

李湘峰，屈莉莉

（佛山科学技术学院自动化系，广东佛山528000）

三相逆变器的结构能控性分析

李湘峰，屈莉莉

（佛山科学技术学院自动化系，广东佛山528000）

针对三相四线制逆变器的结构能控性问题，将其建模为一类状态变量变化连续的混杂系统，同时将混杂系统模型与图论方法结合起来，提出了适用于电力电子变换器结构能控性分析方法，并利用该方法分析了三相四线制逆变器的结构能控性，最后用切换线性系统能控性理论与仿真，验证了图论方法分析的可行性与正确性。

三相四线制逆变器；结构能控性；切换线性系统

任何有效的控制策略均是建立在系统能控基础之上的，能控性分析在系统设计中占据着至关重要的地位。电力电子变换器能控性问题，大多是从电路学角度进行分析并提出解决方案［1-2］，或是在状态空间平均模型下运用线性系统能控性理论进行研究并指导设计［3］。也有学者从拓扑学、图论角度对开关变换器控制特性进行分析［4］，并提出将拓扑学图论用于电路设计与故障诊断［5］。然而，这些研究大部分忽略了变换器模态切换的动态过程，其研究结果具有一定的局限性。

电力电子变换器实际上是一类包含连续状态变量和离散开关变量的混杂系统。为此，胡忠波等人将切换线性系统理论引入DC-DC变换器的分析与控制［6-8］，运用切换线性系统理论对DC-DC变换器进行建模以及研究其能控性。切换线性系统电力电子变换器能控性理论是一种较系统且有效的能控性分析方法，为电力电子变换器的结构能控性提供理论支持。结构能控性的概念由LINCT于1974年首次提出［9］，他指出系统结构能控是系统在常值意义下能控的先决条件，并建议将状态方程转换为有向图的形式以便于对系统结构能控性进行分析。结构能控性分析不仅适用于线性系统，而且适用于分散控制系统［10-11］、切换线性系统［12］等，同时也适用于电力电子系统的分析与设计。

对于电力电子变换器这类系结构多变且系统参数不精确的非线性系统，较难用经典控制理论来判别系统的能控性。此外，电力电子系统电路参数总是需要根据实际情况进行调整的比如考虑系统响应、需要更改输出电感、考虑纹波需要更改输出电容等，而主电路拓扑一旦选定不会轻易更改。由此可知，在设计初期研究系统是否能控时，关心系统是否结构能控具有较大的实践意义。本文拟从图论角度考察切换线性系统结构能控性判定原则，并以此对三相四线制逆变器的结构能控性进行分析。

1　切换线性系统的结构能控性

电力电子变换器存在多种工作模态，不同的工作模态对应着不同的电路拓扑，注意到系统状态变量是随着时间与输入的改变而连续变化的，体现出连续时间动态特性。离散事件动态特性和连续时间动态相互作用使得电力电子电路呈现出典型混杂系统动态特性，因此可将电力电子变换器建模成切换线性系统，这样更能反映其本质，方便分析系统的结构能控性。一般来说，切换线性系统数学模型可表示为

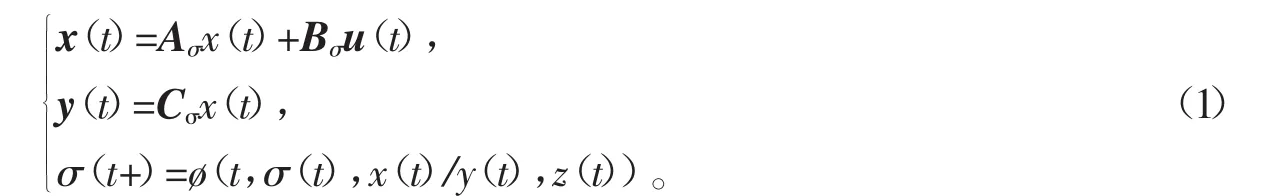
其中，x∈Rn为系统状态向量；u∈Rp为系统输入向量；y∈Rq为系统输出；Aσ为系统状态系数矩阵；Bσ为系统输入矩阵；Cσ为系统输出矩阵；z（t）为外部输入信号，如外部干扰、状态观测器的输出等；σ∈m为控制变换器各模态交替工作的切换信号；m∈N+为系统工作模态个数。

本文主要讨论开关变换器的结构能控特性，与系统输出方程及控制方程无关，因此只需研究如下所示状态方程

结构能控性分析方法所考虑的一般是系统结构不发生变化的情况，即系数矩阵中非零项的位置与个数不发生变化。而电力电子变换器工作时电路工作模态不断更替，且各个子模态状态方程中非零项的数目和位置是不一致的，也就是说系统在工作期间，其系统结构是不断变化的。从模型（1）可以看出，系统同时拥有多个子系统，即拥有多组［，若将其依次描述为图的形式将获得多组能控性图，图间联系难以建立。

为了将这这些图合并以方便研究系统的结构能控性，可将系统为变形为

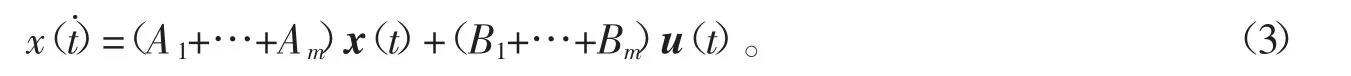
式（2）与（3）所示系统能控特性存在一定的联系，他们之间的关系可由下述推论来描述。

推论若式（3）所示系统是能控的，则式（1）所示切换线性系统亦是能控的。

证明对于式（3）所示系统，其能控性矩阵可表示为

展开式（4）可得

已知系统（3）能控，则能控性矩阵（4）秩为n，已知式（1）所示切换线性系统能控性矩阵可表示为

显然，对式（6）所示能控性矩阵做适当线性变换能得到式（5），由于线性变换不改变矩阵的秩，即rank（Qc1）=rank（Qc），而rank（Qc1）=n。因此根据切换线性系统能控性理论可知式（1）所示切换线性系统是结构能控的。由此可知，可将式（2）所示系统转变为式（3）所示系统进行能控性分析。

2　三相四线制逆变器结构能控性分析

电力电子变换器是典型的切换系统，同时，在电力电子变换器设计初期，能确定的只是电路的拓扑结构，而很多参数都是待定的。因此，只能根据电路的拓扑结构研究其结构能控性问题，图1为三相四线制逆变器电路。

图1　三相四线制逆变器电路结构

根据电力电子变换器潜电路分析软件分析结果可知，图1中拓扑结构的逆变器共有8个有效工作模态，选取状态变量为ib、ic分别为三相输出电感电流，ua、ub、uc分别为三相输出电容电压，可得其状态系数矩阵与系统输入矩阵如下

式（9）转换为能控性图如图2所示。

图2可视为由三颗“仙人掌”构成，为了便于研究系统的结构能控性，可对图2有向边进行适当删减，从而得到其简化形式如图3所示。

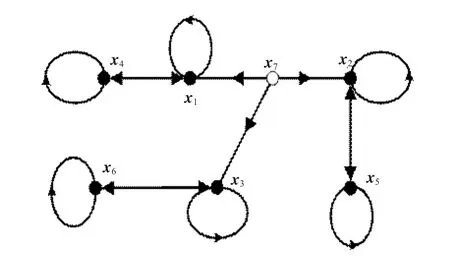
图2　结构能控性图

图3简化后的结构能控性图

图3中，x7为原点，x1～x6是状态变量。从图3知，系统由（x7→x1→x4）、（x7→x2→x5）、（x7→x3→x6）3条“茎”组成，其中状态变量x1、x2、x3、x4、x5、x6分别位于3条“茎”上，因此系统是结构能控的。

3　仿真分析

能控性在实际运行中表现为系统是否能跟踪给定。针对三相四线制逆变器是否能控的问题，可利用仿真软件Matlab/Simulink来检验前述理论分析的正确性。

逆变器仿真参数设置如下：输入电压Vin=700V，三相输出滤波电感L=3mH，滤波电容C=2.2μF，线路等效电阻r=100mΩ。仿真时为检验逆变器能控特性，将三相逆变器的平衡点设置为｛22A，11A，11A，220V，220V，220V｝，即设置三相输出电压对称，有效值为220V，选择三相负载分别为Ra=10 Ω，Rb=20Ω，Rc=20Ω，对于三相四线制逆变器采用PID控制，可得其仿真结果如图7所示。

图4三相逆变器仿真结果

图4a所示为三相四线制逆变器输出电压与输出电流波形，图4b所示为输出电流与电流给定之间的差值，图4c所示为输出电压与电压给定之间的差值。从图4仿真结果可以看出，对于三相四线制逆变器，其状态变量可以通过适当的控制收敛到给定的平衡点，即系统是结构能控的。

4　小结

本文所采用的有向图是由状态方程得到的，相比直接从电路得到的有向图包含更多的信息量，因而更能反映出系统运作的本质。同时，由于该图论法不需要电路的精确参数，而特别适合于设计初期电力电子变换器的结构能控性分析。但系统结构能控只是确定了系统存在能控的可能性，并不保证对于任何结构参数系统均是能控的，为此对于参数具体化的系统仍需用切换线性系统能控性理论检查其能控性。此外，结构能控性图示法不仅能判别系统在结构上是否存在能控的可能性，对于不可控的系统还能找出不可控的状态变量以及不可控的原因，从而为系统的改进提供直观的图形参考，这将为电力电子电路拓扑设计提供一定的理论指导。

［1］彭力，白丹，康勇，等.三相逆变器不平衡抑制研究［J］.中国电机工程学报，2004，24（5）：174-178.

［2］孙驰，马伟明，鲁军勇.三相逆变器输出电压不平衡的产生机理分析及其矫正［J］.中国电机工程学报，2006，26（21）：57-64.

［3］向礼丹.嵌入Boost电路的矩阵变换器（BoostMC）基础理论研究［D］.湘潭：湘潭大学，2008.

［4］VEERACHARY M， SENJYU T, UEZATO K. Signal flow graph nonlinear modelling of interleaved converters ［J］. IEE ProcElectr Power Appl， 2001， 148（5）： 410- 418.

［5］涂文娟，丘东元，张波.DC/DC谐振开关电容变换器潜电路发生的一般规律分析［J］.电工技术学报，2007，22（12）：98-104.

［6］］HU Zongbo， ZHANG Bo， DENG Weihua. Output controllability of switched power converters as switched linear systems［C］//IEEE 4th IPEMC’04. Xi’an： IEEE， 2004： 1665- 1668.

［7］］XIAO Wenxun， ZHANG Bo， QIU Dongyuan. Control strategy based on discrete- time Lyapunov theory for DC- DC converters［C］//The 33rd Annual Conference of the IEEE Industrial Electronics Society（IECON）. Taipei： IEEE， 2007： 1501- 1505.

［8］SUN Zhengdong， SHUZHI S G. Switched Linear Systems： Control and Design［M］. Germany： Springer- Verlag， 2005： 3- 18.

［9］CHING- TAI LIN. Structural Controllability［J］. IEEE Transactions on Automatic Control， 1974， 19（3）： 201- 208.

［10］K H， Y T. Graph- theoretic approach to controllability and localizability of decentralized control systems ［J］. IEEE Transactions on Automatic Control， 1982， 27（5）： 1096- 1108.

［11］RECH C， PERRET R. About structural controllability of interconnected dynamical systems ［J］. Automatic， 1991， 27（5）：877- 881.

［12］LIU Xiaomeng， LIN Hai， CHEN BM. Graphic interpretations of structural controllability for switched linear systems［C］//201011th International Conference on Control Automation Robotics &Vision（ICARCV）. Singapore： IEEE， 2010： 549- 554.

【责任编辑：任小平renxp90@163.com】

Study on structural controllability of three-phase three-w ire inverter

LI Xiang-feng，QU Li-li

（School of Automation Engineering，Foshan University，Foshan 528000，China）

In order to study the controllability of three-phase three-wire inverter，the inverter was modeled as a type of hybrid system which had no abrupt change of the state variables.Thereafter，based on the hybrid system model，the structural controllability of the three-phase three-wire inverter was studied by the graph theory approach.The research results show that the three-phase three-wire inverter is structural controllable. Simulations based on simulink was conducted to verify the correctness of the analysis.

three-phase four-wire inverter；structural controllability；switched system

TM464

A

1008-0171（2016）05-0006-05

2016-06-06

国家自然科学基金资助项目（51277030）；广东省自然科学基金资助项目（2016A030310241）；广东省高等学校高层次人才资助项目（2050205-194）

李湘峰（1983-），男，湖南邵阳人，佛山科学技术学院讲师，博士。