基于导数光谱融合建模的红外光谱定量分析方法

李志刚彭思龙杨妮王巧云吕江涛呼晓飞(东北大学信息科学与工程学院，沈阳089)　(中国科学院自动化研究所，北京0090)(上海市计量测试技术研究院，上海00)

基于导数光谱融合建模的红外光谱定量分析方法

李志刚*1彭思龙2杨妮3王巧云1吕江涛1呼晓飞1
1(东北大学信息科学与工程学院，沈阳110819)2(中国科学院自动化研究所，北京100190)3(上海市计量测试技术研究院，上海201203)

设计了基于奇摄动技术的导数光谱估计器并提出基于不同阶次导数光谱空间的融合建模定量分析方法。方法充分利用导数光谱信息空间、区间最小二乘法和融合建模的优点，挖掘光谱深层次信息进行融合建模。分别利用麦汁浓度范围4．23～18．76°P(柏拉图度)的啤酒红外光谱公共数据集和配制的浓度为0．04%～5%范围的葡萄糖溶液实测光谱数据集进行定量分析方法的对比实验。实验结果表明，融合建模定量分析方法能获得最小的预测均方根误差(RMSEP)，其值分别为0．121和0．087，能够准确地进行定量分析。与其它建模方法相比较，基于导数光谱的融合建模方法所建立的预测模型具有明显优越的性能。

定量分析;奇摄动技术;导数光谱;区间偏最小二乘;融合建模

1　引言

目前，光谱分析技术广泛应用于食品、药品、环保监测以及医疗诊断分析等领域［1～11］。如何挖掘光谱信息，建立精确、稳定的分析模型是应用领域中最为关切的问题。因此利用光谱进行定量分析的关键是从光谱中充分提取建模所需的有效信息［12，13］。光谱定量分析中最常用的预处理方法是导数光谱［14］。导数光谱不但可以消除基线漂移的影响，还可在一定程度上能够区分混叠谱峰，提高光谱的分辨率［15～18］。但是，导数运算过程中不可避免地放大了高频噪声成分，使其在实际应用中受到了很大的束缚。SG(Savitzky-Golay)算法是获取导数光谱方面里程碑式的突破［19］。但是其数据截断的缺陷，多项式阶次与数据窗口宽度参数缺乏标准化选取方法的不足，以及噪声抑制能力的欠缺，使其不适用于处理带有高噪声的实测光谱。

针对从噪声光谱中获取高质量导数光谱的难题，本研究设计了基于奇摄动技术的导数光谱估计器DSE(Derivative spectra estimator)，为建模分析提供丰富有效的导数光谱信息。此外，波长和变量选择也是提高建模分析质量的常用手段，但其缺陷是存在丢失有用信息的风险。融合建模方法则通过一系列子模型的加权融合技术形成最终的融合模型，即有效抑制了干扰信息的影响又最大程度避免了信息丢失的风险［20］。但是，目前的融合模型均为单一光谱空间的子模型融合，对光谱信息挖掘不足。本研究提出并实现了基于不同导数光谱信息空间的融合建模策略DSF-iPLS(Derivative spectra fusion interval PLSmodeling)，在各自导数光谱信息空间子模型加权融合的基础上，再次进行不同阶次导数光谱信息空间模型的二次融合，深度挖掘光谱信息，形成最终的融合模型，进一步了提升模型的质量。

2　数据与方法

2．1光谱数据集

为了测试DSE的基本性能以及验证DSF-iPLS在光谱定量分析中的普遍应用效果，利用两个含有噪声的溶液光谱数据集进行验证。数据集1，实验室配制的23个葡萄糖水溶液，溶剂是去离子水，浓度在0．04%～5%之间。葡萄糖水溶液的红外光谱由带有衰减全反射ATR采样附件(ZnSe cell)的Perkin-Elmer Spectrum GX FTIR光谱仪采集得到，全反射16次。谱图的全谱采集范围为4000～650 cm-1，光分辨率和扫描次数分别为4 cm-1和16次。葡萄糖的指纹吸收波段分布在1200～900 cm-1范围。实验环境温度为(23±1)℃，湿度为42%RH。光谱如图1所示。从图1可见，光谱存在较严重的噪声，因此全谱范围建模方法在避免信息丢失的同时不可避免的受到其它因素和噪声的干扰。图2清晰地显示出不同浓度的葡萄糖溶液的红外吸收特性。建模过程中，数据集的划分采用KS(Kennard-Stone)算法，选取70%的样本作为校正集，剩余的样本作为验证集［21］。

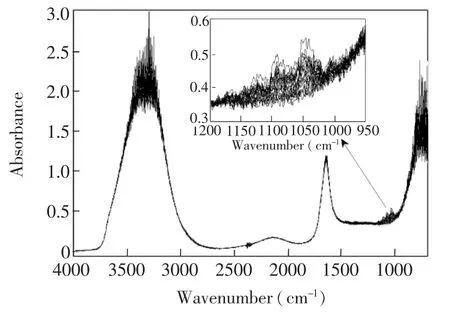
图1　葡萄糖水溶液23个样本红外光谱Fig．1　Infrared spectra of 23 glucose solution samples Insert:Infrared absorption band of glucose．

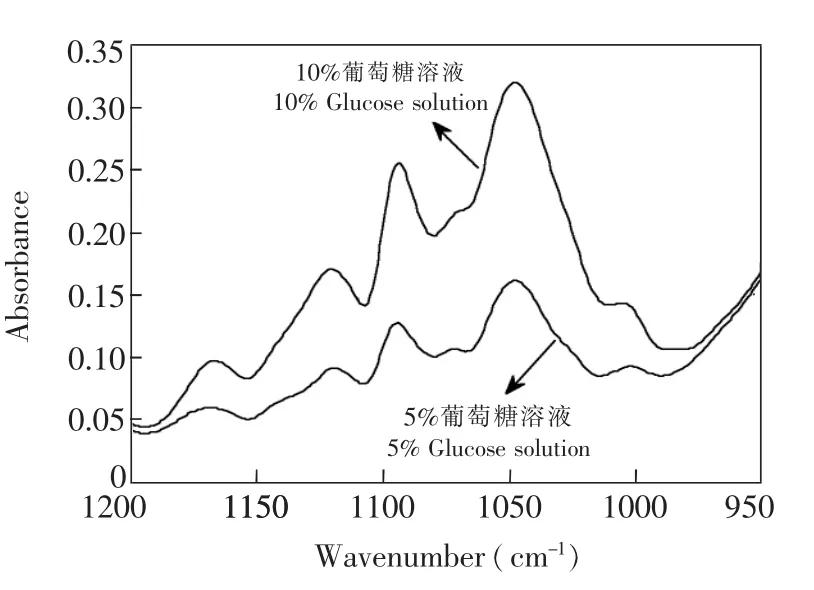
图2　不同浓度葡萄糖的红外吸收谱Fig．2　Absorption spectra of different concentrations of glucose solution

数据集2由60个啤酒样本构成，由Nrgaard教授提供，是近红外与可见共同存在的光谱数据集。啤酒原麦汁浓度范围4．23～18．76°P(柏拉图度)，它是啤酒质量控制的重要指标之一。近红外光谱(包括可见光区域)通过NIR系统分光光度计采集(型号6500)，采集环境温度25℃。分光光度计具有一个分离检测系统，在400～1100 nm范围，用硅(Si)探测器，在1100～2500 nm则用硫化铅(PbS)探测器。通过利用30 mm石英样品池采集未稀释的脱气啤酒的近红外与可见光区域透射光谱信息［22］。光谱波长范围从400～2250 nm，间隔2 nm，光谱数据转换成吸收光谱，每个样本波长数为926。啤酒数据集光谱如图3所示。

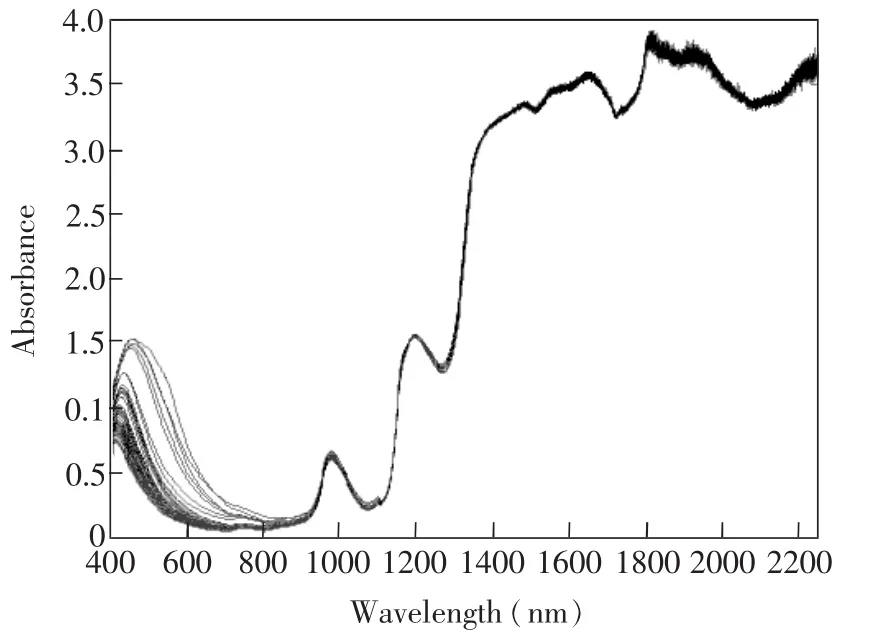
图3　60个样本啤酒光谱Fig．3　Spectra of sixty beer samples

在400～700 nm的可见光区域，由于样本中同时存在淡啤酒和浓啤酒，因此存在大量变量。在1350 nm以上区域主要是水吸收，高吸收导致了高噪声。在970 nm位置，主要是水OH的二倍频峰(羟基峰)，光谱其它部分主要是CH和NH伸缩振动的倍频峰。光谱低端主要是大量的变量而高端主要是测量噪声。建模过程中，啤酒数据集按照原麦汁浓度从低到高进行排序，从第二个样本开始每隔三个样本取一个(即2，5，59，……)作为测试集，其余样本作为校正集，即40个为校正样本，20个为预测样本［23］。

2．2基于奇摄动技术的导数光谱估计器

光谱分析应用领域中导数光谱有着广泛的应用。而实测光谱常带有噪声，基于直接数值差分方法求取信号导数的运算过程中不可避免地放大了噪声成分，难以实际应用。SG(Savitzky-Golay)算法如前文所述，其不适用于处理含有高噪声的实测光谱。奇摄动是一种求解微分方程渐进解的方法。依据多尺度的特征，奇异摄动技术可以将复杂问题分解为简单问题进行处理，广泛的应用在化学、物理与信号处理等领域。针对实测光谱高质量导数谱获取的难题，依据文献［24］设计了基于奇摄动技术和泰勒级数的高精度、抗扰性强的导数光谱估计器DSE。假设信号u(v1)在任意v1的值是已知的。令v1=v+Δv，Δv是足够小。已知u(v)以及其n阶导数，根据泰勒级数u(v1)近似表达为:方程(1)意味着一个信号可由其极小邻域内的信号及其各阶导数高度近似。反之，如果令u(v1)=(v)是实测含噪光谱信号，而其不含噪声的光谱信号u(v)以及其n阶导数未知。令Δv=ε，作为摄动参数;令xi(v)=ui－1(v)，其中ui－1(v)是i－1阶导数，截取到三阶近似，则方程(1)转换为如下线性微分方程，

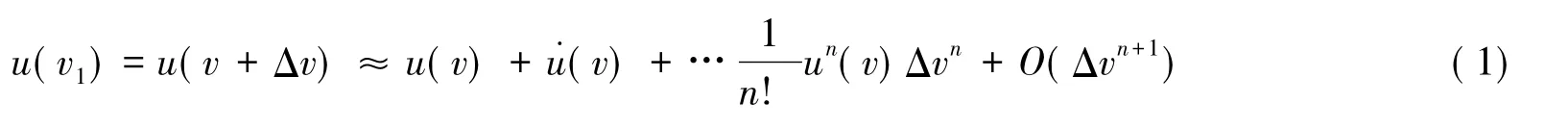
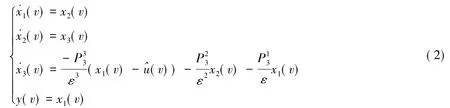
因此，x1是(v)的零阶导数(平滑)信号。此外，(v)只出现在最后的微分方程中，信号中大量的加性噪声经过连续的积分环节后被消除。当摄动参数ε足够小时，xi可以精确估计(v)的零阶导数、一阶导数和二阶导数。DSE只有一个调节参数，克服了参数选择的限制，利于进一步实现算法优化。

2．3参数选择与计算

DSE实际应用中，越大，消噪能力越好。但摄动参数选取不当会产生严重的信号失真。本文利用预测均方根误差RMSEP(Root Mean Square Error of Prediction)和交叉验证均方根误差RMSECV(Root mean square error of cross validation)两个模型评价指标作为参数ε选取的标准。在SG算法中，通过大量实验来确定多项式阶次和窗口宽度参数。窗口点数实验范围为3～81个，多项式阶次实验范围为0～5。在建立PLS模型时，要避免主成分个数选择不当引起的过拟合或欠拟合。因此，主成分的选择需要在最小化预测残差平方和PRESS(Prediction residual error sum of squares)与降低模型复杂度之间寻求一个折中。葡萄糖溶液和啤酒数据集的显著度水平都选择为0．25［25］。利用RMSEP、RMSECV、决定系数R2(Coefficient of determination)以及相对分析误差RPD(Ratio of performance to standard deviate)作为模型的主要评价指标。

2．4导数光谱信息空间融合建模

融合建模已经成为提升模型品质的常用方法。通过区间的优化组合，各类叠加、融合的建模算法被广泛的应用与研究［26，27］。这些算法一定程度上提高了模型的稳健性和预测性能，但是多数算法是利用区间偏最小二乘法iPLS(Interval partial least squares)实现同一光谱空间不同区间组合方式的融合建模，因此存在一定的局限性，对光谱信息挖掘不足。主要代表性的此类算法有叠加偏最小二乘法SPLS (Stacked partial least squares regression)和双层叠加偏最小二乘法DSPLS(Dual stacked partial least squares)［28，29］。本研究将重点研究利用不同阶次的导数光谱信息空间进行融合建模的策略DSF-iPLS，深入挖掘光谱在不同导数空间的信息特征，达到进一步提炼光谱特征信息，提高模型性能的目的。本研究利用DSE获得导数光谱信息，在同一个导数光谱信息空间内部进行子区间划分及独立建模，然后对此空间所建立的子区间模型进行加权融合，形成对应于该导数光谱信息空间的初级融合模型。这个加权过程称为DSF-iPLS内加权，子区间模型的RMSECV被用来评估每个子区间模型的预测性能，内部加权的子模型的权值表达为:

其中，ekj代表第k阶导数谱空间的第j个子模型对应的PLS交叉校验误差，ekj=RMSECVkj，k=0，1，2，j=1，2，……，m。其后，将不同阶次导数光谱信息空间所对应的初级融合模型作为新的子模型进行不同导数光谱信息空间的外部加权融合，得到最终的预测模型。DSF-iPLS外部加权的权值表达为:

在此过程中，交叉验证误差仍然作为评价建模效果的指标，其中ek=RMSECVk，k=0，1，2。其中wk≥0且w0+w1+w2=1。最终融合模型的模型精度评价指标为RMSEP，计算公式如下:其中，nrest是测试集样本数，yref是实际值，ypre是模型预测值。

3　结果与讨论

3．1葡萄糖配制溶液实验结果

在各阶次导数谱空间，进行iPLS内部加权融合建模，权值主要依赖各个子区间模型的RMSECV值，主要目的是既不丢失建模信息，又通过赋予干扰信息区间极小的权重充分抑制干扰信息。依据内部融合模型的RMSEP以及RMSECV评价指标，确定零阶导数光谱空间的区间数(Interval number)为10个子区间;一阶导数光谱空间为25个子区间;二阶导数光谱空间为14个子区间。各导数光谱空间的区间iPLS建模效果如图4～6所示，图中，灰色柱为子区间PLS建模所对应的RMSECV值，是下一步融合建模的关键指标。曲线则为多个样本导数谱的平均谱线。为了更好说明DSF-iPLS全谱融合的优势，以零阶导数谱(平滑)为例，显示融合过程中间环节的建模效果，即光谱子区间建模效果。将整个光谱波数范围分为10个子区间。区间偏最小二乘模型的RMSEP值如图7所示，其中预测性能最好的区间数为第9区间，其RMSEP值为0．183。

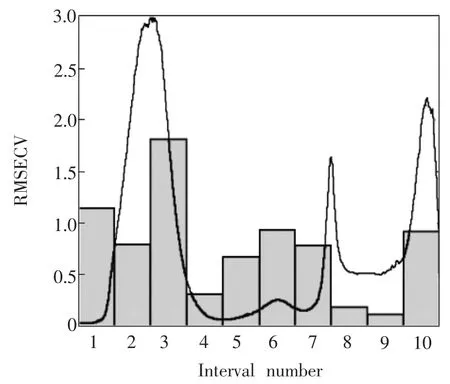
图4　葡萄糖零阶导数谱(平滑)iPLS模型RMSECVFig．4　Rootmean square error of cross validation(RMSECV)for intervalmodels of zero-order derivative spectra of glucose

图5　葡萄糖一阶导数谱iPLS模型RMSECV(A)和二阶导数谱iPLS模型RMSECV(B)Fig．5　RMSECV for intervalmodels of first-order derivative spectra(A)and second-order derivative spectra (B)of glucose

葡萄糖溶液导数光谱融合建模(DSF-iPLS)与未经过任何预处理的PLS模型以及SPLS，DSPLS等不分区间的全谱融合模型的预测性能比较，实验结果见表1，DSF-iPLS全谱融合模型提供最低的RMSEP值0．121，远低于平滑谱子区间建模的最优建模结果0．183。葡萄糖配制溶液光谱定量分析实验的统计结果初步验证了DSF-iPLS方法的有效性和优越性，其预测性能超过了SPLS和DSPLS算法。

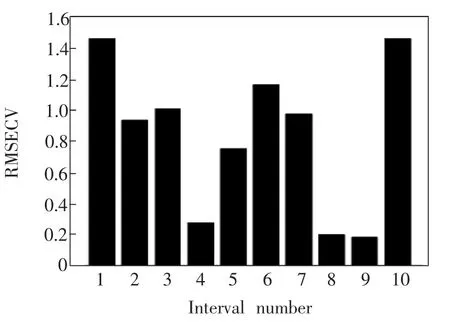
图6　葡萄糖平滑谱区间偏最小二乘(iPLS)模型预测性能Fig．6　Rootmean square error of prediction(RMSEP)for intervalmodels of zero-order derivative spectra of glucose

表1　葡萄糖溶液数据集DSF-iPLS与其他方法建模结果Table 1　Analysis results of glucose dataset by derivative spectra fusion interval partial least squares(DSF-iPLS) and othermethods

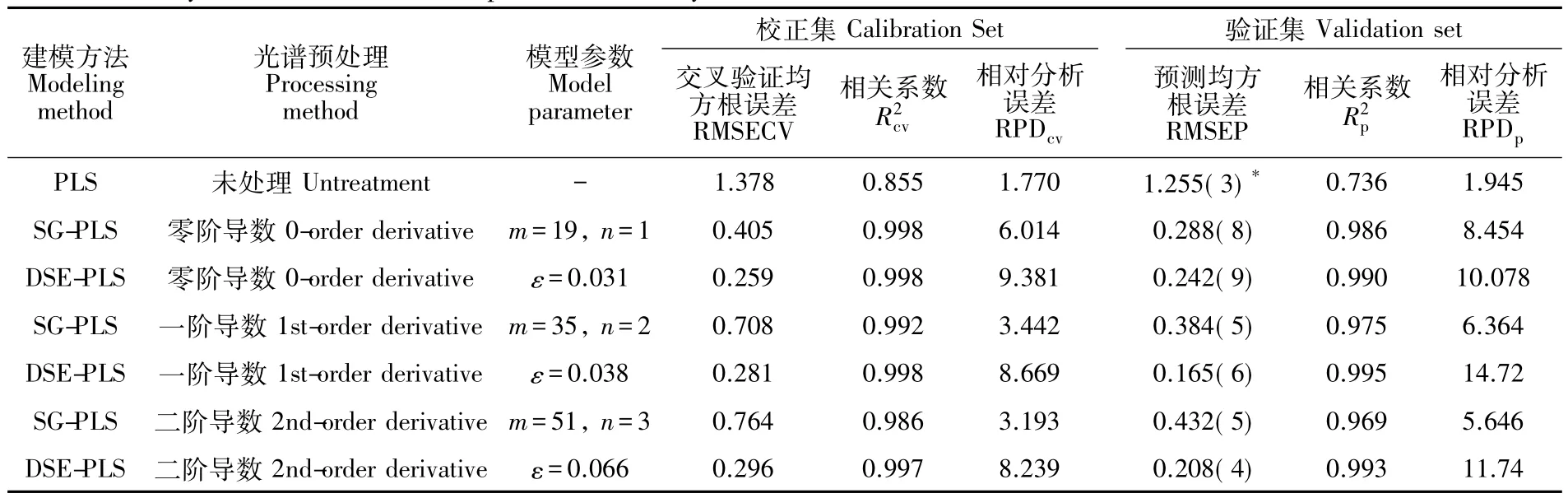
表2　啤酒数据集建模分析结果Table 2　Analysis results of the beer spectra data set by PLS

3．2啤酒光谱实验结果

为了进一步系统详尽地验证基于DSE的DSF-iPLS的性能，以啤酒光谱数据集作为研究对象。首先，验证原始光谱的PLS模型对啤酒原麦汁浓度的预测性能;然后，分别利用SG和DSE方法获取啤酒光谱的零阶导数光谱空间、一阶导数光谱空间和二阶导数谱空间，在各自导数光谱空间建立全谱PLS预测模型并进行比较。较低的RMSEP和RMSECV值代表更好的预测能力，较高的R2和RPD(RPDcv:校正集RPD值，RPDp:测试集RPD值)则说明模型具有较强的鲁棒性和适用性。一般而言，RPD＞3的模型认为是较为成功的模型，RPD＞5则可用于质量控制等领域。比较结果见表2，原始光谱PLS模型，预测结果不理想。DSE-PLS模型优于传统SG-PLS模型。SG方法导数光谱PLS模型RPDcv＜5，显然这类模型不适合应用在定量分析领域。在上述验证结论基础上，对DSF-iPLS与SPLS和DSPLS进行比较。DSF-iPLS确定零阶导数光谱空间为12个子区间;一阶导数光谱空间为20个子区间;二阶导数光谱空间为8个子区间。将上述3个不同阶次导数光谱空间所建立的初级融合模型，进行不同阶次导数光谱空间外部融合，得到最终融合模型。实验结果见表3，3种不同PLS集成建模方法预测能力有较大差别。对于预测模型来说，RMSEP值越低，表明模型预测能力越好。实验结果表明SPLS、DSPLS方法与PLS方法相比较RMSEP有所降低，模型预测能力有所改善。在所有提到的方法中，DSF-iPLS能够获得最低的RMSEP，具有最优越的预测性能。

表3　啤酒数据集DSF-iPLS与其它方法建模结果Table 3　Analysis results of beer data set by DSF-iPLSand othermethods

4　结论

实测光谱中存在大量不相关的信息和噪声，DSF-iPLS将光谱分割成若干建模子区间，依据每个子区间不同的建模效果赋予子区间模型不同的权重进行融合建模，加强了有效信息区间的权重;弱化了噪声区间和干扰区间的权重，最大程度上避免了有效信息丢失的风险。同时，不同导数光谱信息空间的融合又为进一步挖掘光谱特征信息开辟了空间，扩充了样本空间信息含量，从而能够获取更好的预测能力。然而，在这一领域仍然有许多问题需要进一步研究。未来的工作将继续完善和开发基于不同阶次导数光谱信息空间的融合建模策略，设计更加合理的子模型筛选与加权机制，构建性能更优越的融合模型。

References

1Ribeiro JS，Ferreira M M C，Salva T JG．Talanta，2011，83(5):1352－358

2Jaiswal P，Jha SN，Borah A，Gautam A，Grewal M K，Jindal G．Food Chem．，2015，168:41－47

3HeiseH M，Marbach R．Anal．Chem．，1989，61(18):2009－2015

4LIYan，WU Ran-Ran，YU Bai-Hua，WANG Jun-De．Spectroscopy and Spectral Analysis，2006，26(10):1846－1849李燕，吴然然，于佰华，王俊德．光谱学与光谱分析，2006，26(10):1846－1849

5ZUO Qi，CHEN Yao，SHICai-Xia，CHEN Zeng-Ping．Chinese J．Anal．Chem．，2015，43(11):1656－1663左奇，陈瑶，石彩霞，陈增萍．分析化学，2015，43(11):1656－1663

6WANG Lei，GUO Shu-Xia，DAI Yin-Zhen，YANG Liang-Bao，LIU Guo-Kun．Chinese J．Anal．Chem．，2015，43(1): 33－39王磊，郭淑霞，戴吟臻，杨良保，刘国坤．分析化学，2015，43(1):33－39

7Polshin E，Aernouts B，Saeys W，Delvaux F，Delvaux F R，Saison D，Hertog M，Nicolai B M，Lammertyn J．J．Food Eng．，2011，106(3):188－198

8Giovenzana V，Beghi R，Guidetti R．J．Food Eng．，2014，142:80－86

9Shen F，Ying Y B，Li B B，Zheng Y F，Hu JG．Food Res．Int．，2011，44(5):1521－1527

10Liao，Chien-Sheng，Slipchenko M N，Wang P．Light-Sci．Appl．，2015，4:e265

11SUN Yuan-Tao，ZHANG Hong-Tian．Chin．J．Lumin．，2015，36(3):366－369孙远涛，张洪田．发光学报，2015，36(3):366－369

12GAO Rong-Qiang，FAN Shi-Fu，YAN Yan-Lu，ZHAO Li-Li．Spectroscopy and Spectral Analysis，2004，24(12):1563－1565高荣强，范世福，严衍禄，赵丽丽．光谱学与光谱分析，2004，24(12):1563－1565

13LIU Wei，ZHAO Zhong，YUAN Hong-Fu，SONG Chun-Feng，LI Xiao-Yu．Spectroscopy and Spectral Analysis，2014，34(4):947－951刘伟，赵众，袁洪福，宋春风，李效玉．光谱学与光谱分析，2014，34(4):947－951

14Rinnan，van den Berg F，Engelsen SB．TRAC-Trend．Anal．Chem．，2009，28(10):1201－1222

15KharintsevSS，Kamalova D I，Salakhov M K．Appl．Spectrosc．，2000，54(5):721－730

16Wang SC，Lin C J，Chiang SM，Yu SN．Anal．Chem．，2008，80(6):2097－2104

17Ojeda C B，Rojas F S．Anal．Chim．Acta，2009，635(1):22－44

18Rojas F S，Ojeda C B．Microchem．J．，2013，106:1－16．

19Savitzky A，Golay M JE．Anal．Chem．，1964，36(8):1627－1642

20Mevik B H，Segtnan V H，Ns T．J．Chemometr．，2004，18(11):498－507

21Kennard RW，Stone L A．Technometrics，1969，11:137－148

22Nrgaard L，Saudland A，Wagner J，Nielsen JP，Munck L，Engelsen SB．Appl．Spectrosc．，2000，54(3):413－419

23Indahl U．J．Chemometr．，2005，19(1):32－44

24Li ZG，Ma ZH．Circ．Syst．Signal Process．，2014，33(2):589－598

25Haaland D M，Thomas E V．Anal．Chem．，1988，60(11):1193－1202

26Breiman L．Mach．Learn．，1996，24(1):49－64

27Moreira JM，Soares C，Jorge A M，Sousa JF．ACM Comput．Surv．，2012，45(1):10－40

28NiW D，Brown SD，Man R．J．Chemometr．，2009，23(10):505－517

29Bi Y M，Xie Q，Peng S L，Tang L，Hu Y，Tan J，Zhao Y H，Li CW．Anal．Chim．Acta，2013，792:19－27

This work was supported by the National Natural Science Foundation of China(No．11404054)，and the Natural Science Foundation of Hebei Province(Nos．F2016501138，F2014501127)

Quantitative Analysis Method of Infrared Spectra Based on Derivative Spectra Fusion M odeling

LIZhi-Gang*1，PENG Si-Long2，YANG Ni3，WANG Qiao-Yun1，LJiang-Tao1，HU Xiao-Fei1
1(College of Information Science and Engineering，Northeastern University，Shenyang 110819，China)2(Institute of Automation，Chinese Academy of Sciences，Beijing 100190，China)3(Shanghai Institute of Measurement and Testing Technology，Shanghai 201203，China)

A derivative spectral estimator(DSE)based on singular perturbation techniquewas designed and a quantitative analysis method based on derivative spectra information space，termed derivative spectra fusion interval partial least squares(DSF-iPLS)modeling was proposed．DSF-iPLSmainly focused on obtaining final fusion model bymaking full use of derivative spectra information．The glucose spectra datasetwith concentrate ranging from 0．04%to 5%and the beer spectra dataset with the original extract concentration ranging from 4．23 to18．76°P(Plato)were used to evaluate the effectiveness of the proposed quantitative analysismethod．The experiment results indicated that DSF-iPLSmodel for two infrared spectra datasets provided theminimum rootmean square error of prediction(RMSEP)and the valueswere 0．121 and 0．087，respectively．Compared with other single model，DSF-iPLSmodel based derivative spectra could provide more excellent predictive performance．

Quantitative analysis;Singular perturbation technique;Derivative spectra;Interval partial least squares;Fusion modeling

28 September 2015;accepted 15 December 2015)

10．11895/j．issn．0253-3820．150765

2015-09-28收稿;2015-12-15接受

本文系国家自然科学基金(No．11404054)和河北省自然科学基金项目(No．F2016501138，F2014501127)资助

*E-mail:lizgqhd@163．com