基于样本差异的多标签分类器评价标准预估
2016-11-09余圣波
张 敏 余圣波
(重庆大学计算机学院软件理论与技术重庆市重点实验室 重庆 400044)
基于样本差异的多标签分类器评价标准预估
张敏余圣波
(重庆大学计算机学院软件理论与技术重庆市重点实验室重庆 400044)
评价标准是分类器的重要指标。对于多标签学习,常用的评价标准有Hamming Loss、One-error、Coverage、Ranking loss和Average precision。多标签分类器给出分类结果的同时并未给出评价标准值,通常采用事后验算的方法评估评价标准。这样往往不能及时有效地发现评价标准值变化之类的问题,同时评估评价标准值需对测试样本进行标记。针对这一问题,分别从样本分布差异和样本实例间差异提出两种评价标准预估方法。分析上述两种方法的特点,提出第三种评价标准预估方法。实验表明,这三种评价标准预估方法具有良好效果,可用于迁移学习等。
多标签学习评价标准样本分布样本实例线性拟合
0 引 言
多标签学习是机器学习和数据挖掘技术中的一个研究热点。与单标签学习相比,多标签分类中的样本可以同时归属多个类别。多标签学习是一种更符合真实世界客观规律的方法,其广泛地应用于各种不同的领域,如图像视频的语义标注[1-3]、功能基因组[4,5]、音乐情感分类[6]以及营销指导[7]等。多标签学习主要有两个任务:多标签分类和标签排序[8],前者的任务就是要为每一个样本尽可能地标注出所有与其相关的标签,从而达到一个多标签自动分类的目的;后者则是对于待测样本按标签与其相关程度由高至低输出全部标签。
现有的多标签数据的学习方法主要分为两大类:问题转换法和算法适应法[9]。问题转换的方法就是通过改造数据将多标签学习问题转化为其他已知的单标签学习问题进行求解,该方法不受特定算法的限制,目前已成熟的单标签分类算法有支持向量机、k近邻方法、贝叶斯方法和提升方法等。算法适应方法是通过直接改造现存的单标签学习算法,使之能够适应多标签数据的处理,该类方法代表性的学习算法有ML-kNN(Multi-Label k-Nearest Neighbor)[10]、RankSVM(Ranking Support Vector Machine)[11]、AdaBoost.MH(multiclass,multi-label version of AdaBoost based on Hamming loss)[12]和BoosTexter (A Boosting-based System for Text Categorization)[13]等。在本文中,使用ML-kNN分类算法得到多标签评价标准值。ML-kNN是kNN算法的扩展,其性能优于BoosTexter、AdaBoost.MH和 RankSVM。
多标签学习的评价指标不同于传统的单标签学习,单标签学习常用的评价标准有准确度、精度、召回率和F值[14]。对于多标签学习,常用的评价标准有Hamming loss、One-error、Coverage、Ranking loss和Average precision。其中,Hamming loss主要衡量预测所得标签和样本实际标签不一致的程度,结果越小越好;One-error描述样本预测隶属度最高的标签不在实际标签的概率,结果越小越好;Coverage描述了在标签排序函数中,从隶属度最高的标签开始,平均需要跨越多少个标签才能覆盖样本所拥有的全部标签,结果越小越好;Ranking loss衡量样本所属标签隶属度低于非其所属标签隶属度的概率,结果越小越好;Average precision描述了对样本预测标签的平均准确率,结果越大越好。
目前要得到多标签学习评价标准有两个常用方法。一个常用的方法是观察训练样本集中的评价标准值,训练样本集中的评价标准值与测试样本集中的评价标准值无明确关系,但是通过对训练样本集中的评价标准值的观察,估计测试样本集中的评价标准值有一定意义。对于Hamming loss、One-error、Coverage和Ranking loss,这些评价标准关于测试样本集的值往往高于或等于这些评价标准在训练样本集中的估计值,那么关于训练样本集的这些评价标准值过高,其在测试样本集中的评价标准估计值也不会低。对于Average precision评价标准,其关于测试样本集的估计值往往低于或等于其在训练样本集中的估计值,那么Average precision在训练样本集中的估计值太低,其在测试样本集中的估计值也不会高。另一个常用的方法是标记测试样本,与分类结果对比,得到测试样本的评价指标值,然后利用统计学的知识,将计算出来的评价指标值推广到一般情况。这种方法需要标记测试样本,标记样本有时候会比较昂贵,但其得到的评价指标估计值比较客观。可以看出,想得到关于测试样本集的确切评价指标值,往往需要对测试样本进行标记,那么是否可以不对测试样本进行额外的标记就估计出关于测试样本的评价指标值呢?
本文提出基于测试样本与训练样本差异来估计关于测试样本的评价指标的方法。样本差异可以从宏观和微观两个角度来考虑,样本分布差异是样本差异的宏观体现,样本实例间差异是样本差异的微观体现。这样可以通过收集到的测试样本与训练样本的对比估计出评价指标值,从而避免标记样本的昂贵成本,使得多标签分类器可以在给出分类结果的同时给出评价标准估计值,可以应用于迁移学习等领域。
1 基于样本分布差异的多标签评价标准预估
1.1MMD统计量
通常情况下,分类器都假设样本分布在整个分类过程中不会发生变化。当训练样本集和测试样本集的分布有差异时,由训练样本集得到的分类器不再适用于测试样本集。如单标签贝叶斯分类器,当训练样本集和测试样本集的分布有差异时,先验概率发生变化,此时由训练样本集得到的贝叶斯分类器不适用于测试样本集。那么如何衡量两组样本的分布差异呢?
设有一组训练样本集记为A(x1,x2,…,xm),其服从分布p;一组测试样本记为B(y1,y2,…,yn),其服从分布q。如何判断p和q是否相同,过去主要采用参数统计的方法,首先需要确定它们的分布模型,之后通过参数假设的方法推断它们是否包含相同的参数。文献[15]提出了将分布嵌入再生核希尔伯特空间的方法。文献[16]提出了衡量两组样本差异的核方法,即最大均值差异MMD(Maximum Mean Discrepancy)的度量方法。其中:
(1)
式中,F为将测量空间映射到实数域的一类函数,k(·)为核函数。
(2)
式中,K为一常数,且|k(x,y)|≤K,x∈A,y∈B。
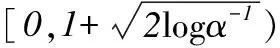
1.2MMD与评价标准的关系
为了确定MMD统计量与多标签评价标准Hamming loss、One-error、Coverage、Ranking loss和Average precision 的关系,使用参数估计的方法估计评价标准。从评价标准和MMD统计量的实验数据可以看出,MMD与Hamming loss、One-error、Coverage、Ranking loss和Average precision有良好的线性关系。然而,针对不同的评价标准,相关性程度也不相同。可将使用MMD估计多标签评价标准值问题假设为:
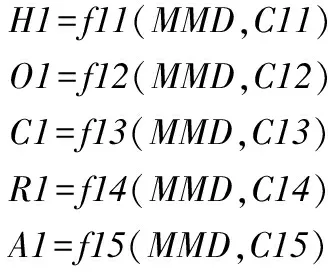
(3)
其中H1、O1、C1、R1和A1分别为Hamming loss、One-error、Coverage、Ranking loss和Average precision的估计值。C11、C12、C13、C14和C15为参数列表;f11、f12、f13、f14和f15为线性函数。为了确定参数估计中的相关参数和使得评价标准与评价标准估计值的误差最小,使用最小二乘法。下面以评价指标Hamming loss为例进行求解,其他指标的求解过程与Hamming loss相似。设有z1组实验数据(mmdi,hlossi),i=1,…,z1,它们相互独立,其中mmdi和hlossi分别为第i次实验得到的MMD统计值和Hamming loss值。记:
则残差平方和为:
Q1=‖Y-X×C11‖2=(Y-X×C11)′(Y-X×C11)

2 基于样本实例间差异的多标签评价标准预估
2.1MMR统计量
MMD关注的是训练样本集和测试样本集的分布差异,是一个宏观的统计量。样本差异可以从宏观和微观两个角度进行考虑。样本实例间差异是样本差异的微观体现。为此,提出基于样本实例间差异的多标签评价标准估计。
k近邻算法kNN(k-nearest neighbor)是一种基于样本实例的单标签分类器。k近邻算法意味着每个样本都可以用与它最近的k个邻居来表示,其基本思想是:找到离该样本最近的k个邻居,如果这k个邻居大多数属于某一个类别,那么这个样本也应该属于这个类别。k近邻分类算法的数学模型如下:设一组训练样本集记为A(x1,x2,…,xm),一组测试样本集记为B(y1,y2,…,yn),为了求得B中每个样本yi的标签,对每个测试样本做如下处理:求得训练样本集A中与yi最接近的k个样本,然后由这k个样本投票得到yi的标签。对k近邻算法的一个明显改进是对k个近邻进行距离加权。离测试样本越近的训练样本,其权值越大。可以看出,在k近邻算法中,若近邻与测试样本的平均距离越小,则分类结果的可信度越高。使用kNN算法得到一个分类结果,该分类结果的可信度可以由k近邻组成的邻域大小做出估计。此处,选择k=1的特殊情况。如果对测试样本B中的每一个样本yi,与其在A中的最近邻样本xj的距离d(yi,xj)足够小,那么以xj的标签作为yi的标签有较高的可信度;反之,与其在A中的最近邻样本xj的距离d(yi,xj)比较大,那么以xj的标签作为yi的标签具有较低的可信度。
由此假设,B中样本与A中样本的最小距离影响kNN算法分类结果可信度。通过观察B中每个样本到A中样本的最小距离,可以得到B中样本的kNN分类结果可信度。由这个估计得到对多标签分类器评价标准的估计。本文提出了MMR(Mean Maximum Resemblance)统计量,MMR为B中样本到A中样本最小距离的均值。
MMR(A,B)=mean(minx∈Ad(x,y))
(4)
MMR的计算方法如下:
Step1对yi∈B,i=1,2,…,n,计算其与训练样本集的最小距离:
md(yi)=minxj∈Ad(xj,yi)
=minxj∈A(xj-yi)×(xj-yi)′j=1,2,…,m
(5)
Step2求均值:
(6)
Step3标准化:
(7)
在Step3中使用最大跨度作为标准化分母,使得MMR尽量不受训练样本集的影响。MMR越大,表示测试样本集与训练样本集实例间的差异越大,随之关于测试样本集的Hamming loss值、One-error值、Coverage值和Ranking loss值越大,Average precision值越小;MMR越小,表示测试样本集与训练样本集实例间的差异越小,随之关于测试样本集的Hamming loss值、One-error值、Coverage值和Ranking loss值越小,Average precision值越大。
MMR性质:MMR(A,B)=0,当且仅当对于测试样本集中的每一个实例,在训练样本集中都可以找到与之相同的实例,使得它们的距离为0,即MMR(A,B)=0。MMR(A,B)不是一个对称的统计量,即MMR(A,B)≠MMR(B,A)。一个特例是A真包含B时,有MMR(A,B)=0,MMR(B,A)≠0。MMR的计算时间复杂度为O(mn+m2)。
2.2MMR与评价标准的关系
为了确定MMR和多标签评价标准的关系,使用参数估计的方法估计评价标准。从多标签评价标准和MMR统计量的实验数据可以看出,Hamming loss、One-error、Coverage、Ranking loss、Average precision和MMR统计量也有良好的线性关系。然而,对于不同的评价标准,相关性程度也不同。因此,跟利用MMD统计量估计评价标准类似,可将评价标准估计问题假设为:

(8)
其中H2、O2、C2、R2和A2分别为Hamming loss、One-error、Coverage、Ranking loss和Average precision的估计值;C21、C22、C23、C24和C25为参数列表;f21、f22、f23、f24和f25为线性函数。为了确定参数估计中的相关参数和使得评价标准与评价标准估计值的误差最小,亦使用最小二乘法。下面以Hamming loss为例进行求解,其他评价指标的求解过程与Hamming loss相似。设有z2组实验数据(mmrj,hlossj),j=1,2,…,z2,它们相互独立,其中mmrj和hlossj分别为第j次实验得到的MMR统计值和Hamming loss值。记:
则残差平方和为:
Q2=‖Y-X×C21‖2=(Y-X×C21)′(Y-X×C21)

3 基于MMD和MMR的多标签评价标准预估
MMD关注的是训练样本集和测试样本集的分布差异,是一个宏观的统计量;MMR关注的是训练样本集中的实例和测试样本集中的实例之间的差异,是一个微观的统计量。它们可以相互补充,共同估算出关于测试样本集的评价标准值。
由利用MMD线性拟合评价标准和MMR线性拟合评价标准,可以得出Hamming loss、One-Error、Coverage、Ranking loss和Average precision分别与MMD和MMR的相关方程及参数。利用这些参数,可以得出这些评价标准与MMD和MMR的相关方程。由于MMD和MMR都与这些评价标准有良好的线性关系,故将使用MMD和MMR预估多标签评价标准问题假设为:

(9)
其中H3、O3、C3、R3和A3分别为Hamming loss、One-error、Coverage、Ranking loss和Average precision的估计值。c311、c312、c313、c321、c322、c323、c331、c332、c333、c341、c342、c343、c351、c352和c353为参数列表;f31、f32、f33、f34和f35为线性函数。下面以Hamming loss为例进行参数求解,其他评价标准的参数求解过程与Hamming loss相似。

(10)
线性方程f31的详细表达式如下:
H3=c311+c312×MMD+c313×MMR
(11)
4 实验及分析
4.1实验说明
在实验中共使用两组数据集,分别描述如下:
UJIndoorLoc数据集是一个基于WLAN/WiFi指纹的多建筑多层室内定位数据集。 该数据集有两组数据,分别叫做UJI_training和UJI_test。UJI_training含有19 937个训练样本,UJI_test含有1111个测试样本。
Turkiye学生评价数据集由 Gazi University提供。该数据集有两组数据,分别叫做Tu_training和Tu_test。Tu_training收集于2013年,有5820个学生评价数据;Tu_test收集于2014年,有5820个学生评价数据。这两组数据有差异。
共进行16次试验,分别记为Task1,Task2,…,Task16。采用ML-kNN多标签分类器得出关于测试样本集的评价标准值。
4.2样本差异与MMD、MMR的关系
Task1~Task6使用相同的训练样本集,得到相同的分类器。从UJI_training set中随机抽取1200个样本作为Task1至Task6的训练样本集。从UJI_test set中进行两次随机抽取200个样本分别作为Task1和Task2的测试样本集。从UJI_training set中(除Task1的训练样本集)进行两次随机抽取200个样本分别作为Task3和Task4的测试样本集。从Task1和Task3的测试样本集中各随机抽取100个样本,再将它们合并,作为Task5的测试样本集;从Task2和Task4的测试样本集中各随机抽取100个样本,再将它们合并,作为Task6的测试样本集。然后,得到MMD值和MMR值,使用ML-kNN得到Hamming loss、One-error、Coverage、Ranking loss和Average precision的值。实验结果如表1所示。从表1可以看出,UJI_training set和UJI_test set存在差异。不同地点采取的数据可能存在差异。

表1 Task1~Task6实验结果
Task7-Task12使用相同的训练样本集,得到相同的分类器。从Tu_training set中随机抽取1200个样本作为Task7至Task12的训练样本集,从Tu_test set中进行两次随机抽取200个样本分别作为Task7和Task8的测试样本集。从Tu_training set(除Task7的训练样本集)中进行两次随机抽取200个样本分别作为Task9和Task10的测试样本集。从Task7和Task9的测试样本集中分别随机抽取100个样本,再将它们合并,作为Task11的测试样本集。从Task8和Task10的测试样本集中分别随机抽取100个样本,再将它们合并,作为Task12的测试样本集。然后,得到它们的MMD值、MMR值和多标签评价标准值,实验结果如表2所示。从表2可以看出,Tu_training set和Tu_test set两组数据存在差异。Tu_training set采集于2013年,Tu_test set采集于2014年。
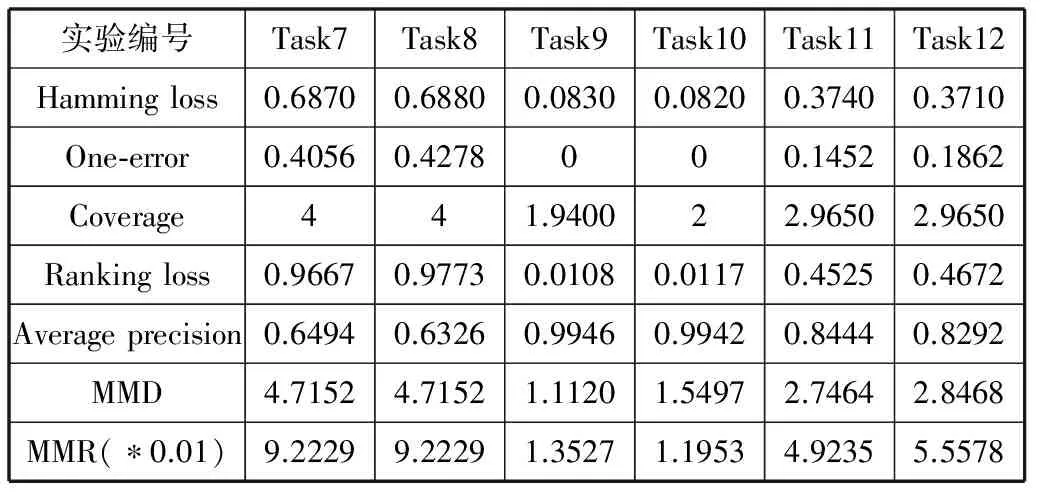
表2 Task7~Task12实验结果
从表1和表2可以看出,MMD能正确反映两组样本分布的差异, MMD值越小,表示训练样本集和测试样本集的分布差异越小,从而Hamming loss、One-error、Coverage、Ranking loss的值越小,Average precision的值越大。MMD值越大,表示训练样本集和测试样本集的分布差异越大,从而Hamming loss、One-error、Coverage、Ranking loss的值越大,Average precision的值越小。MMR能正确地反映两组样本实例间的差异,MMR越大,表示训练样本集实例和测试样本集实例之间的差异越大,从而Hamming loss、One-error、Coverage、Ranking loss的值越大,Average precision的值越小。MMR越小,表示训练样本集实例和测试样本集实例之间的差异越小,从而Hamming loss、One-error、Coverage、Ranking loss的值越小,Average precision的值越大。
4.3评价标准估计
Task13采用UJIndoorLoc数据库。从UJI_training set中随机抽取801个样本作为Task13的训练样本集。为保证数据的平衡性,从UJI_training set(除Task13的训练样本集)中随机抽取1111个样本和UJI_test set作为一个新的测试样本集,记为Test samples1。从Test samples1中随机抽取90个样本作为Task13的测试样本集。重复20次,然后得到MMD值、MMR值和多标签评价标准值。利用4-折交叉验证得到评价标准的估计值。
Task14采用UJIndoorLoc数据库。从UJI_training set中随机抽取1200个样本作为Task14的训练样本集。为保证数据的平衡性,从UJI_training set(除Task14的训练样本集)中随机抽取1111个样本和UJI_test set作为一个新的测试样本集,记为Test samples2。从Test samples2中随机抽取250个样本作为Task14的测试样本集。重复20次,然后得到MMD值、MMR值和多标签评价标准值。利用4-折交叉验证得到评价标准的估计值。
评价标准估计的实验结果如表3所示,其中EM(D)为使用MMD估计评价标准的误差均值,EM(R)为使用MMR估计评价标准的误差均值,EM(D,R)为使用MMD和MMR估计评价标准的误差均值。

表3 Task13~Task14实验结果
从表3和表4可以看出,针对不同的评价标准,MMD的表现不同。其中,对于Hamming loss、One-error、Ranking loss和Average precision,MMD的表现良好。对于Coverage,MMD的表现要比其他评价标准差。针对不同的评价标准,MMR的表现也不同。对于Hamming loss、One-error、Ranking loss和Average precision,MMR的表现良好。对于Coverage,MMR的表现要比其他评价标准差。综合使用MMD和MMR估计评价标准的误差均值一般在单独使用MMD和MMR估计评价标准的误差均值之间。对比表3和表4可以看出,训练样本集和测试样本集中的样本数目越多,估计评价指标的误差均值越小。
Task15采用Turkiye Student Evaluation Data Set。从Tu_training set中随机抽取801个样本作为Task15的训练样本集。将Tu_training set(除Task15的训练样本集)和Tu_test set作为一个新的测试样本集,记为Test samples3。从Test samples3中随机抽取90个样本作为Task15的测试样本集。重复20次,然后得到MMD值、MMR值和多标签评价标准值。利用4-折交叉验证得到评价标准的估计值。
Task16采用Turkiye Student Evaluation Data Set。从Tu_training set中随机抽取1200个样本作为Task16的训练样本集。 将Tu_training set(除Task16的训练样本集)和Tu_test set作为一个新的测试样本集,记为Test samples4。从Test samples4中随机抽取250个样本作为Task16的测试样本集。重复20次,然后得到MMD值、MMR值和多标签评价标准值。利用4-折交叉验证得到评价标准的估计值。评价标准估计的实验结果如表4所示。
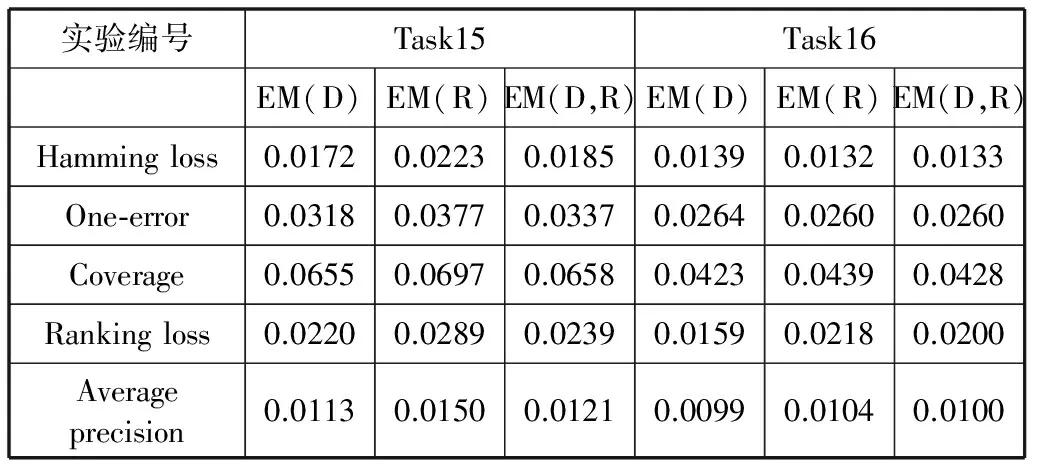
表4 Task15-Task16实验结果
表4得出的信息与表3得出的信息相同。针对不同的评价标准,MMD和MMR的表现不同。其中,对于Hamming loss、One-error、Ranking loss和Average precision,MMD和MMR的表现良好;对于Coverage,MMD和MMR的表现要比其他评价标准差。综合使用MMD和MMR估计评价标准的误差均值一般在单独使用MMD和MMR估计评价标准的误差均值之间。训练样本集和测试样本集中的样本数目越多,估计评价指标的误差均值越小。
通过上述实验结果可以看出,使用MMD线性估计评价标准和使用MMR线性估计评价标准的效果良好。综合使用MMD和MMR线性估计评价标准的效果良好。因此,使用这三种方法估计评价标准是有一定意义的。MMD度量训练样本集和测试样本集之间的分布差异,MMR度量训练样本集实例和测试样本集实例之间的差异,与分类器无关,因此适用于所有的分类器。但由于分类器的性能不同,评价标准估计误差会有一定的波动。
5 结 语
目前并没有专门针对多标签分类器评价标准进行良好估计的方法。本文针对这一问题,提出多标签学习评价标准估计方法。从样本分布差异得出MMD线性估计评价标准的方法,从样本实例间差异得出MMR线性估计评价标准的方法。MMD着眼于两组样本的分布差异,是一个宏观的统计量;MMR着眼于两组样本实例间的差异,是一个微观的统计量。接着综合使用MMD和MMR线性估计多标签分类器的评价标准,其误差均值在单独使用MMD线性估计评价标准和MMR线性估计评价标准的误差均值之间。实验表明,这三种估计方法具有良好的效果,可用于迁移学习等。
[1] Zhang M L, Zhou Z H. ML-kNN:A lazy learning approach to multi-label learning [J]. Pattern Recognition, 2007,40(7):2038-2048.
[2] Xu X S, Jiang Y, Peng L, et al. Ensemble approach based on conditional random field for multi-label image and video annotation[C] // Proceedings of the 19th ACM International Conference on Multimedia, Scottsdale, USA, 2011:1377-1380.
[3] Wang J D, Zhao Y H, Wu X Q, et al. A transductive multi-label learning approach for video concept detection [J]. Pattern Recogintion,2011, 44(10-11):2274-2286.
[4] Nicolo C B, Claudio G, Luca Z. Hierarchical classification:combining Bayes with SVM [C] //Proceedings of the 23rd International Conference on Machine learning, Pittsburgh, USA, 2006:177-184.
[5] Li G Z, You M Y, Ge L, et al. Feature selection for semi-supervised multi-label learning with application to gene function analysis [C] //Proceedings of the 1st ACM International Conference on Bioinformatics and Computational Biology, Niagara Falls, USA, 2010:354-357.
[6] Sanden C, Zhang J Z. Enhancing multi-label music genre classification through ensemble techniques [C] //Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR’ 11), Beijing,China, 2011:705-714.
[7] Zhang Y, Burner S, Street W N. Ensemble pruning via semi-definite programming [J]. Journal of Machine Learning Research, 2006,7(7):1315-1338.
[8] Tsoumakas G, Katakis I, Vlahavas I. Mining multi-label data[M]2nd ed. Data Mining and Knowledge Discovery Handbook, Springer, 2010:667-685.
[9] Grigorios T, Ioannis K. Multi-label classification:an overview [J]. International Journal of Data Warehousing and Mining, 2009,3(3):1-13.
[10] Zhang M L, Zhou Z H. A k-nearest neighbor based algorithm for multi-label classification [C] //Proceedings of the 2005 IEEE International Conference on Granular Computing. Beijing:IEEE, 2005,2:718-721.
[11] Elisseeff A, Weston J. A kernel method for multi-labelled classification [C] //Proceedings of the Advances in Neural Information Processing Systems. Cambridge:MIT Press,2002:681-687.
[12] Schapire R E, Singer Y. Improved boosting algorithm using confidence-rated predictions [J]. Machine Learning,1999,37(3):297-336.
[13] Schapire R E, Singer Y,Carbonell J,et al. BoosTexter:a boosting based system for text categorization [J]. Machine Learning,2000,39(2-3):135-168.
[14] Sebastiani F. Machine learning in automated text categorization[J]. ACM Computer Surveys, 2002,34 (1) :1-47.
[15] Alex S, Arthur G, Le S, et al. A hilbert space embedding for distributions[C] //Proceedings of the 18th International Conference on Algorithmic Learning Theory, 2007:13-31.
[16] Arthur G, Karsten M B, Malte R, et al. A kernel method for the two-sample-problem[C] //Proceedings of the Advances in Neural Information Processing Systems 19, 2007:513-520.
[17] 陈昊. 加权K-NN及其应用[D].保定:河北大学,2005.
ESTIMATING EVALUATION METRICS OF MULTI-LABEL CLASSIFIERS BASED ON SAMPLES DIFFERENCE
Zhang MinYu Shengbo
(Software Theory and Technology Chongqing Key Lab,College of Computer Science,Chongqing University,Chongqing 400044,China)
Evaluation metrics play an important role in classifiers.Popular evaluation metrics used in multi-label learning include Hamming loss,One-error,Coverage,Ranking loss and Average precision.While the classification results are obtained from multi-label classifier,the values of evaluation metrics will be derived later,usually the evaluation metrics are assessed in the way of checking afterwards.However this sometimes cannot find the problem of the variation in values of evaluation metrics timely and effectively,meanwhile it is necessary to mark the test samples when estimating the values of evaluation metrics.To solve this problem,this paper put forward two methods of estimating the evaluation metrics based on the difference in sample sets distribution and on the difference between instances in sample sets respectively.After analysing the characteristics of above two methods,we propose the third estimating method for evaluation metrics.Experiments show that the proposed three methods all have good effects.They can be used in transfer learning and others.
Multi-label learning Evaluation metricsSamples distributionSamples instancesLinear fitting
2015-04-22。中央高校基本科研业务费专项资金项目(CDJZR12180005);重庆自然科学基金项目(CSTC2011BB2063)。张敏,讲师,主研领域:机器学习。余圣波,硕士。
TP3
A
10.3969/j.issn.1000-386x.2016.09.064
