基于邻域几何特征约束的植株三维形态配准方法研究
2016-11-09马福峰张志毅
马福峰 耿 楠 张志毅
(西北农林科技大学信息工程学院 陕西 杨凌 712100)
基于邻域几何特征约束的植株三维形态配准方法研究
马福峰耿楠*张志毅
(西北农林科技大学信息工程学院陕西 杨凌 712100)
为提高不同角度多次测量得到的植株点云配准速度和精度,提出一种基于植株点云邻域几何特征约束改进的三维形态配准方法。首先,针对点云量大并缺少拓扑信息,选取关键点集并估计其中每个点的支撑邻域来拟合出支撑曲面,进一步计算出邻域几何特征。其次,采用特征相似度的方法实现点云的初始配准。最后,在初始配准的基础上,加入两个新的夹角几何特征约束匹配点对改进ICP算法进行配准优化。利用bunny、兵马俑模型点云对算法的精度和通用性进行测试,并在实际应用中验证了配准效果和算法鲁棒性。结果表明,与传统的特征配准方法相比,该方法配准速度提高约10%以上,精确配准误差约为传统算法误差的1%。
三维形态配准几何特征特征相似度迭代最近点算法
0 引 言
虚拟植株研究、植株的三维形态重构以及植株三维形态可视化是当前国内外农业生成信息化研究的重点领域。为了能够获得植株完整的三维形态的点云模型,三维形态的配准也成为了热门的研究领域。近年来,由于物体的表面特征在配准过程中表现出的优势,基于特征的配准方法越来越受到重视。在特征配准中主要是搜索有效的匹配特征点对,当前用于相应匹配点寻找问题的方法旨在减少用来寻找匹配点的点对数量:(1) 通过在数据点集中采样;(2) 使用特征提取方法[1,2]。准确快速获取特征点对成为基于特征三维形态配准算法研究的重点。
三维形态配准一般包括初始配准和精确配准。针对初始配准算法,研究者利用不同的几何特征做了大量的研究。Zhang等[3]利用点云中心提出中心重合法。罗先波[4]和吴敏[5]等通过在模型表面添加标签来突出其特征,提出标签法。戴静兰等[6]利用每片点云三维形态坐标在空间中拟合曲面的法向量作为点云的主方向,并根据该几何特征构造坐标系,提出主方向贴合方法。Diez[8]等分别利用点云的曲率和法向提出基于轮廓线法和利用分层的法向空间采样的方法实现点云初始配准。Dai等[9]也提出基于局部几何特征来完成初始配准。综上,现有的初始配准主要采用基于几何特征的配准,主要包括以下步骤:(1) 提取待配准点集的几何特征;(2) 根据几何特征相似性确立匹配点对;(3) 根据建立的对应关系计算坐标变换参数,并进行初始配准。
常用的精确配准方法是由Besl等[10]和Chen等[11]提出的迭代最近点ICP(Iterative Closest Point)算法,但是经典的ICP算法计算效率低,并且其配准过程是一个迭代收敛的过程,算法的效率受点云初始位姿的约束,也容易陷入局部最优[12,13]。由于它的突出优点,ICP算法又非常具有吸引力,因此国内外研究者在ICP算法基础上,通过引入几何特征来改进算法,并做了大量工作。Chen和Mediomni等[14]提出了用点云的切平面来逼近点云,该方法选取了点到匹配点处的切平面的距离来代替点到点的距离,但是该算法速度较慢,并且物体表面变化明显时会影响收敛。Du等[15]首先通过ICA(Independent Component Analysis)获得点云初始位置,并把放射变换和原始ICP相结合提出放射ICP(Affine ICP)算法。Zhu等[16]提出一个基于双向距离场的配准算法。Jiang等[17]提出了一种基于夹角的点云配准方法,它通过选择点云中的任意点与其邻近点法向之间的夹角作为配准的几何信息,但是,选取特征不明显的点估计法向时可能受到噪声的干扰。Du[18]提出了一种新的局部几何特征描述子“放射形状分布”来表达每个点和它的邻域的随机空间划分,该方法在点集中存在较大的离异值和丢失点的情况下能够检测到对应点对,并求得潜在的点云间坐标变换。但是,该方法对位姿抖动敏感。当然也有很多研究者从不同的最优策略出发,在试探性的变换下应用一个目标函数测量待拼接点云的不同。Myronenko[19]提出了相关点漂移算法(CPD),该方法使用一个点集来表达高斯混合模型,并且把点云配准问题转换为拟合模型到点集的问题。类似的,鲁棒的点云配准方法(RPM-GMM)[20]使用高斯混合模型来最小化两个点集之间的距离。尽管这些方法在许多应用中很成功,但是,如果在点集中离异值和噪声点占得比例过大,这些方法的性能将会严重退化[21]。以上算法主要应用于工业和医学领域,并且都是在尽量减少配准过程中的迭代次数。
由于存在树枝之间的交叉和遮挡的影响,不同角度获得的植株点云结构比较复杂。本文通过对目前三维形态配准方法的分析,并结合植株点云的特征对ICP算法做了以下改进研究:
首先,在初始配准过程中,在选取点云中关键点集的基础上,拟合关键点集的点的邻域曲面计算出几何特征,提出了一种新的几何特征相似度度量函数。根据特征的相似度建立特征匹配点对,并计算变换矩阵实现点云的初始配准,能够快速缩小平移旋转错位。
其次,在精确配准的过程中,通过加入两个相邻匹配点与初始配准后坐标系原点组成的矢量之间的夹角,以及匹配点法向之间的夹角两个几何特征来改进ICP算法,以提高配准的速度和精度。本文方法不需要在测体表面做标记信息,仅通过估计点云自身隐含的几何特征就能够实现点云的精确配准,并且对点云初始位置没有要求。
1 基于几何特征植株三维形态配准方法
三维扫描仪在不同的视角获得物体点云的过程中存在着旋转和平移错位,因此不同视角下的点云在两套坐标系下点坐标的测量值间存在误差。使用最小二乘方法对误差进行求解建模,能够计算出误差最优解[6,10]。基于邻域几何特征约束的植株三维形态配准方法是由邻域几何特征的估计和提取、初始配准和精确配准组成。在初始配准过程中通过特征相似度建立匹配点之间的对应关系。
1.1特征点集提取和特征估计
根据获得的点云邻域,为了方便提取空间中的三维点云数据的几何特征[1],由于在不同局部坐标系下获得物体的点云中特征点之间的相互位置和拓扑关系并没有改变,利用这种空间特征的拓扑不变性就可以找到匹配的特征点对。
点云的邻域特征主要包括邻域点数量、邻域质心、点位于邻域的法向和曲率。其前三个特征是比较明显的,且较容易计算。法向和曲率在消除错误匹配点对和搜索最佳匹配对中发挥重要作用。对于散乱的点云数据,使用最小二乘拟合方法求解法向量和曲率的速度快,且抗干扰性强。本文使用拟合曲面来获得法向量[22,23]。为了适应不同曲面的局部形状要求,根据文献[24,25]利用最小二乘拟合曲面求解曲率,用二次曲面来表征局部区域,用式(1)-式(4)来计算每个点处的主曲率k1、k2、平均曲率H及高斯曲率K:
(1)
(2)
(3)
(4)
此方法计算得到的曲面法矢量的方向具有不一致性,法向方向的不一致影响到曲率计算和消除错误匹配对,因此需要对不协调的法向进行调整。本文使用了Hoppe等[26]提出的“法向传播思想”处理法向方向不一致问题。然后,进一步计算得到曲面的第一和第二基本量L=fxxn,N=fyyn,M=fxyn,E=fxfx,F=fxfy,G=fyfy,代入式(1)-式(3),其中:fx、fy、fxx、fyy、fxy是曲面的偏微分。
1.2基于特征相似度的匹配点对确立以及加权采样
1.2.1加权采样
首先对于曲面不规则的模型都有凸起的区域,这部分区域更有利于特征的提取。本文为了方便提取点云数据特征,对曲面的凸点和凹点加以定义,并去除影响配准精度的凹点,如图1所示。

图1 p是邻域内的点,q是邻域重心,n为点处的法向
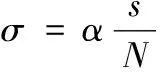
1.2.2特征相似度定义
(5)
本文利用距离函数对每个配准点对进行特征相似度的度量。利用该点的支撑邻域构造该点的特征空间来做两点之间的相似性的判定,该空间是包含所有特征点的高斯曲率均值、平均曲率均值、两个主曲率的均值、法向量夹角的均值的5维空间。
(6)

1.3初始配准

改进初始配准算法步骤如算法1所示。
算法1改进的三维点云数据初始配准算法
输入:
P={pi∈R3}:目标点云数据集。
Q={qi∈R3}: 参考点云数据集。
算法
1: for p∈{pi}do
2: Nk=operaNear(p)and ci=center(Nk)
3: 对每个支撑域拟合曲面,计算主曲率k1、k2、高斯曲率K、平均曲率H、法向n。
4: end for
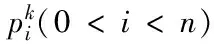
10: end for
11: 根据特征相似度进一步确立特征匹配点,
12: 进一步使用四元数法计算坐标变换矩阵R和T。
13:将坐标变换矩阵R和T代入三维目标数据点集,完成初始配准。
输出:
1.4精确配准
算法2改进后精确配准ICP算法
输入:
Z=[3,9,12,16,50,100,180]
V=φ
算法:
1:for zi∈Zdo
2:while ((dk-dk+1)<γ)
3:for p∈FirPfdo
5:end for
7:if((sinφ<τ1)&&(sinθ<τ2)&&(|cosφ-cosθ|<τ3))
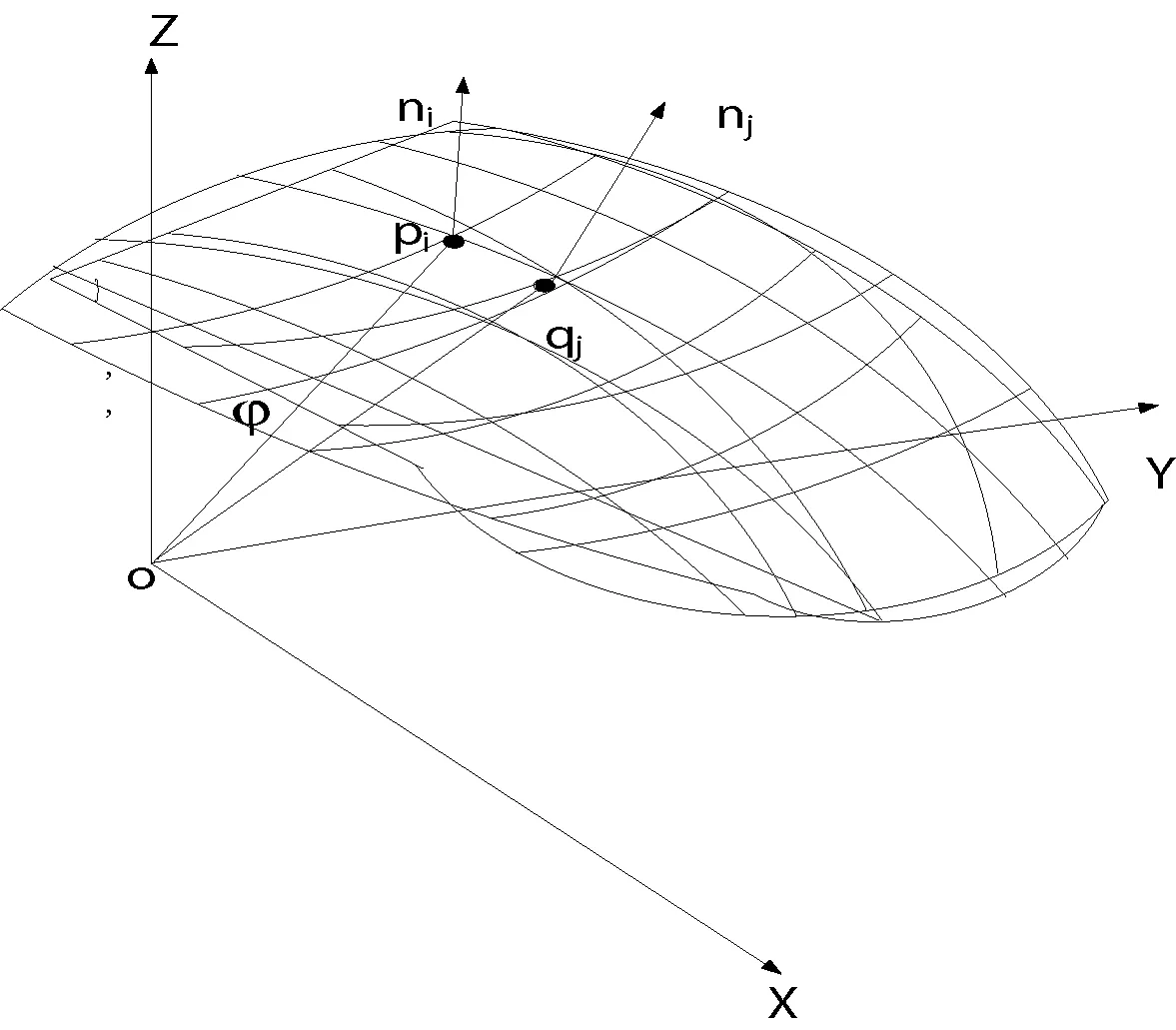
8:if(V.num 10:end if 11:end if 12:if FirPf和FirQf配准误差太大 13:估算变换Tran(R,T)=[QR|QT]T,使得误差趋于最优: 14:应用变换:FirQf(l+1)=Tran(R,T)·FirQf(l), 15:else 16:stop 17:end if 18:对目标点集应用变换,完成精确配准。 图2 初始配准后两个几何特征 19:end while 20:end for 输出:配准后的点云。 本文通过加入φ和θ这两个特征来改进ICP迭代的过程,根据判断这两个特征来进一步优化匹配点对,提高ICP算法的效率。将该方法称为改进的ICP算法,如图2所示。 本实验使用斯坦福大学[27]计算机图形实验室提供的bunny的标准三维点云以及自制设备[28]实际测量兵马俑模型和植株获得的点云。图3是不同视角下获得的点云,其中图3(a)中点云有40 225个三维点,图3(b)中点云有40 096个三维点,图3(c)中点云有90 678个三维点,图3(d)中点云有104 748个三维点,图3(e)、(f)为从不同侧面获得植株模型点云,包含116 386个三维点。实验环境为:系统为Win7,CPU为Intel(R)Core(TM)2.67 GHz,内存为4.00 GB,软件:Microsoft Visual Studio 2010+OpenGL,语言:C++。实验的阈值设定。本文所选取的阈值为:τ1=0.1,τ2=0.2,τ3=0.005,α的值为0.6,考虑到实际点云难以完全满足该约束条件,阈值的选取可以根据实际情况做相应的微调。 图3 不同角度获得的点云 2.1算法对比试验 本实验结合四种算法进行对比实验:1) 采用传统的初始配准算法[6];2) 经典的ICP算法配准[10,11];3) 传统初始配准+经典ICP算法[6];4) 本文提出的算法。为了进行对比,同一组点云被用来作为输入。配准结果如图4所示,配准误差和效率如表1所示。 图4 不同算法点云配准效果比较 算法配准误差d/mm运行时间/s传统初始配准算法6.0132489.43经典ICP算法3.40153258.57初始配准+经典ICP算法1.2036542.14改进初始配准+改进ICP算法0.0124838.46 可以看出:经典ICP算法没有优化点云的初始位置,出现了局部最优的状况,导致配准的精度较低,配准的速度也较慢。本文算法由于在配准之前提取了关键点,并且对点集进行了加权抽样和配准对的优化,减少了配准的数量,即使增加了计算量,计算的时间复杂度也大大降低,同时精度也得到了提高。 2.2不同匹配点对的对比试验 据本文算法设置Z=[3,9,12,16,50,100,180],得到相应的匹配点对,并根据不同的匹配点对计算变换进行配准。经过对Stanford大学提供的点云数据进行试验,验证了该算法在不同特征点对下的配准效果,如图5所示。由表2分析可以看出,只要有三个正确的匹配点就足以计算出最优变换,随着点对的增加,其配准误差变化不大,但是其配准耗时却随着点对的增加不断增加。 图5 bunny不同匹配点对下配准效果对比图 匹配点对数配准误差d/min运行时间/s30.0134736.2390.0124838.46120.0124240.01160.0114342.56500.0104167.311000.0091370.181800.0091190.54 图5(a)所示为原始点云的位姿,图5(b)为使用3对匹配点对情况下配准后的位姿,可以看出,虽然有一定的效果,但是存在偏差,两片点云没有完全重合。图5(c)、(d)是分别在9和12对匹配点下进行的实验,达到了良好的配准效果。图5(e)、(f)、(g)是分别在50、100和180对匹配点下进行的配准,与(c)、(d)相比配准效果相差不大,不过增加匹配点数在一定程度上增加了配准的鲁棒性。图5(h)是在没有提取特征点情况下的配准效果图,与其相比可以反映出本文所提出的算法的性能。 2.3在噪声环境下不同匹配点对的对比试验 为说明该算法的抗噪性能,本实验仍然设置Z=[3,9,12,16,50,100,180],并在相同的实验环境下对含有噪声的兵马俑模型的点云数据进行配准,如图6所示。配准耗时和配准误差如表3所示。 图6 兵马俑模型的含噪声点云数据不同匹配点对下配准效果对比图 匹配点对数配准误差d/mm运行时间/s30.0544840.3190.0513246.23120.0504249.05160.0494353.41500.0404183.211000.0401391.231800.04001113.53 结合图5和图6(b),分析表2和表3可知,特征点对的增加可以提高该算法的抗噪性,但是随着特征点的增加,配准偏差逐渐趋于平稳,表明算法具有抗噪性。噪声对配准误差变化趋势和收敛时间影响如图7所示。 图7 不同匹配点对下配准耗时和误差变化趋势图 2.4在植株点云模型中的应用 为进一步说明该算法在模型配准中的应用,本文选取由自制设备获得的植物模型点云数据和由昆士兰大学提供的树的点云模型进行配准测试。图8(a)、(b)、(c)、(d)、(e)、(f)为自制设备获得点云配准效果图,图8(g)、(h)为昆士兰大学提供的点云进行配准实验的效果图。通过对两组模型的配准分析,验证了该算法对大多数点云模型配准的有效性和通用性。 图8 植株点云模型配准效果 本文提出的特征相似度度量函数方法实现的初始配准和基于夹角几何特征的改进ICP算法的精确配准相结合,能够快速消除三维形态之间的恶旋转和平移错位。本文首先使用标准点云模型测试了算法的效率和精度,最后实际应用到植株的点云模型中。实验结果表明,该算法能够对植株三维形态进行很好的配准。对于含有约4万个数据点的两片点云进行配准,该算法与传统初始配准方法相比速度提高了约50%,与经典ICP算法相比多次测量平均速度约提高了80%,以及与其他改进的ICP方法相比速度约提高了11.95%,配准误差近似。因此该方法在配准的精度和速度上都有了提高,具有实际的应用价值。 [1] Basdogan C,Oztireli A C.A new feature-based method for robust and efficient rigid-body registration of overlapping point clouds[J].The Visual Computer,2008,24(7):679-688. [2] Yang H J,He D J.A simplified and accurate registration for splat-based fruit scans[J].ICIC Express Letters,Part B:Applications,2012,3(4):733-741. [3] Zhang X C,Xi J T,Yan J Q.Research on digital measurement technology based on point cloud data of complex surfaces[J].Computer Integrated Manufacturing Systems,2005,11 (5):727-731,737. [4] 罗先波,钟约先,李仁举,等.三维扫描系统中的数据配准技术[J].清华大学学报:自然科学版,2004,44(8):1104-1106. [5] 吴敏,周来水.测量点云数据的多视拼合技术研究[J].南京航空航天大学学报,2003,35(5):552-557. [6] 戴静兰,陈志杨,叶修梓,等.ICP算法在点云配准中的应用[J].中国图象图形学报,2007,12(3):517-521. [7] Wang Z,Geng N,Zhang Z.Surface mesh reconstruction based on contours[C]//proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering.CiSE 2009,December 11,2009-December 13,2009,Wuhan,China,F,2009,IEEE Computer Society. [8] Diez Y,Marti J,Salvi J.Hierarchical normal space sampling to speed up point cloud coarse matching[J].Pattern Recognition Letters,2012,33(16):2127-2133. [9] Dai J J,Yang J.A novel two-stage algorithm for accurate registration of 3D point clouds[C]//International Conference on Multimedia Technology,2011:6187-6191. [10] Besl P J,Mckay N D.A method for registration of 3d shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256. [11] Chen Y,Medioni G.Object modeling by registration of multiple range images[J].Image and Vision Computing,1992,10(3):145-155. [12] Xie Z X,Xu S,Li X Y.A high-accuracy method for fine registration of overlapping point clouds[J].Image and Vision Computing,2010,28(4):563-570. [13] Liu Y H.Constraints for closest point finding[J].Pattern Recognition Letters,2008,29(7):841-851. [14] Chen Y,Medioni G.Object modeling by registration of multiple range images[C]//Robotics and Automation,1991 IEEE International Conference on.IEEE,1991:2724-2729. [15] Du S Y,Zheng N N,Ying S H,et al.Affine iterative closest point algorithm for point set registration[J].Pattern Recognition Letters,2010,31(9):791-799. [16] Zhu J,Du S,Yuan Z,et al.Robust affine iterative closest point algorithm with bidirectional distance[J].IET Computer Vision,2012,6(3):252-261. [17] Jiang J,Cheng J,Chen X L.Registration for 3-Dpoint clouds using angular-invariant feature[J].Neuro Computing,2009,72(16-18):3839-3844. [18] Du J,Xiong W,Chen W,et al.Multi-view Point Cloud Registration Using Affine Shape Distributions[M]//Computer Vision--ACCV 2014.Springer International Publishing,2014:147-161. [19] Myronenko A,Song X.Point set registration:Coherent point drift[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2010,32(12):2262-2275. [20] Jian B,Vemuri B C.Robust point set registration using gaussian mixture models[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2011,33(8):1633-1645. [21] Lian W,Zhang L.Robust point matching revisited:a concave optimization approach[M]//Computer Vision-ECCV 2012.Springer Berlin Heidelberg,2012:259-272. [22] Joel Daniells,Tilo Ochotta,Linh K,et al.Spline-based feature curves from point-sampled geometry[J].The Visual Computer,2008,24(6):449-462. [23] Guan Y L,Cheng X J.A robust method for fitting a plane to point clouds[J].Joural of Tongji University:Natural Science,2008,36(7):982. [24] Chen Z Q,Wang Y Z,Li B,et al.A survey of methods for moving least squares surfaces[C].Symposium on Point-Based Graphics 2008.Los Angeles:EG&VGTC,2008:9-23. [25] 朱延娟,周来水,张丽艳.散乱点云数据配准算法[J].计算机辅助设计与图形学学报,2006,18(4):475-481. [26] Hoppe H,DeRose T,Duchamp T,et al.Surface reconstruction from unorganized points[J].ACM Siggraph Computer Graphics,1992,26(2):71-78. [27] The Stanford 3D Scanning Repository[EB/OL].Stanford University Computer Graphics Laboratory.[2003-04-01].http://www.graphics.stanford.edu/data/3Dscanrep/. [28] Zhang Z Y,Yuan L.Build A 3D Scanner System Based on Monocular Vision[J].APPLIED OPTICS,2012,51(11):1638-1644. ON 3D PLANT MORPHOLOGY REGISTRATION METHOD BASED ON GEOMETRICAL FEATURE CONSTRAINT OF NEIGHBOURHOOD Ma FufengGeng Nan*Zhang Zhiyi (College of Information Engineering,Northwest Agricultural and Forest University,Yangling 712100,Shaanxi,China) In order to improve the registration speed and precision of plant point cloud derived from multiple measurements in various angles, this paper proposes an improved 3D morphological registration method which is based on the geometrical feature constraint of neighbourhood of plant point clouds. First, aiming at the large amount of point clouds and lack of topological information, the method estimates the support neighbourhood of each point by selecting key point set to fit the support surface and then to further compute the geometrical feature of neighbourhood. Secondly, it employs the feature similarity method to implement the initial registration of point clouds. Finally, based on initial registration it adds two matching pairs of angle’s geometric feature constraints to improve the iterative closest point (ICP) algorithm and to optimise the registration. We tested the accuracy and universality of the algorithm with the point clouds of bunny and Terracotta Army models, and verified in practical application the effect of registration and the robustness of the algorithm. Results showed that compared with traditional feature-based registration method, the proposed method increased the registration speed about over 11.9%, and the error of precise registration was about 1% of that of the traditional feature-based algorithm. 3D morphology registrationGeometrical featureFeature similarityICP algorithm 2015-05-21。国家高技术研究发展计划项目(2013AA 102304);基本科技创新一般项目(QN2013056);科技创新一般项目(2014YB067)。马福峰,硕士,主研领域:计算机虚拟技术与图形学。耿楠,教授。张志毅,副教授。 TP391.41 A 10.3969/j.issn.1000-386x.2016.09.044

2 实验分析









3 结 语
