Delaunay三角剖分算法改进与对比分析
2016-11-09袁小翠吴禄慎陈华伟
袁小翠 吴禄慎 陈华伟
(南昌大学机电工程学院 江西 南昌 330031)
Delaunay三角剖分算法改进与对比分析
袁小翠吴禄慎陈华伟
(南昌大学机电工程学院江西 南昌 330031)
针对Delaunay算法的计算速度问题,从数据结构和算法两个方面加以改进。对Delaunay三角剖分的代数拓扑分析,设计一种顺序存贮的Hash数据结构,实现临时单纯形对象的快速和顺序存取、查询、插入和删除等操作;以单纯形边对象的活性分析为核心,以Hash数据结构进行操作,消去生长法的递归过程;此外,提出基于微切平面的生长法,将基于空间四面体的空球搜索降维至局部二维的空圆搜索。对汽车挡泥板和兔子模型进行三角剖分实验,实验结果表明,消去递归的生长法和基于微切平面的生长法和传统的生长法三角剖分效果相同,但是计算速度比传统方法效率更高。
Delaunay三角剖分生长法半空间隐式曲面
0 引 言
逆向工程通过三维光学扫描仪获取物体形貌数据,该数据通常是海量的三维点,在数据处理中,需要经过三角化、光滑曲面重建才能为正向CAD软件所采用。点云三角化网格重建是数据由离散点域向面域求解的第一步,是后续光滑曲面重构的基础。其重构方法主要有基于Delaunay三角剖分的方法[1,2]、基于区域扩张的方法[3,4]和基于实体布尔差运算的方法[5,6],其中生长法是最常用的Delaunay三角剖分法[7]。目前,已有诸多学者开始采用隐式曲面法[9-11]构造三角剖分。尽管如此,作为三角剖分的基础,Delaunay法仍然集成于主流算法和商品化软件之中,尤其是在国内,Delaunay三角网格构造仍然是一个热点研究问题。作为一个三角网格剖分的基础和共性问题,本文对Delaunay三角剖分中的生长法进行分析,针对Delaunay算法的计算速度问题,设计一种顺序存贮的Hash数据结构,实现临时单纯形对象的快速存取、插入和删除等操作。此外,本文还提出基于微切平面的生长法,将基于空间四面体的空球搜索降维至局部二维的空圆搜索,提高三角剖分的时间效率。
1 Delaunay三角剖分
代数拓扑中,n-单纯形(n-simplex)拓扑等价于n-球面,每个n-单纯形是n维带边界流形。n-单纯形是三角形和四面体的一种泛化,一个n维单纯形是指包含n+1个节点的凸多面体。其精确定义是:n-simplex是某个n维以上的欧氏空间Rd(d≥n)中的n+1个仿射无关的点集的凸包。例如,0-simplex就是点,1-simplex就是线段,2-simplex就是三角形,3-simplex就是四面体。将构成单纯形的各点称为单纯形的顶点(vertex)。进一步地,将单纯形的k+1个顶点的凸包组合所构成的单纯形称为k维面(k-face),如点是0-face,边是1-face,三角面是2-face。
拓扑空间可以通过单纯形组合构造,人们希望把一个拓扑对象剖分成许多个小的单纯形,并要求任何两个相邻单纯形的相交部分仍是一个单纯形——这种剖分称为单纯剖分。在曲面情形,就是三角剖分。
R3空间中面的剖分是2-simplex,即三角形的组合,则相邻单纯形的相交部分为1-face,即为边。三角化过程就是以边为基础,逐步向外扩展生成三角形,新三角形的边将作为继续生长的基础。三角形生长应遵循一定的规则,Delaunay三角剖分规定了两项重要规则:
1) 空圆特性:任一Delaunay三角形的外接圆内不会有其他点存在,如图1(a)所示;
2) 最大化最小角特性:在点集P可能形成的三角剖分中,Delaunay剖分形成的三角形的最小角最大,如图1(b)所示。
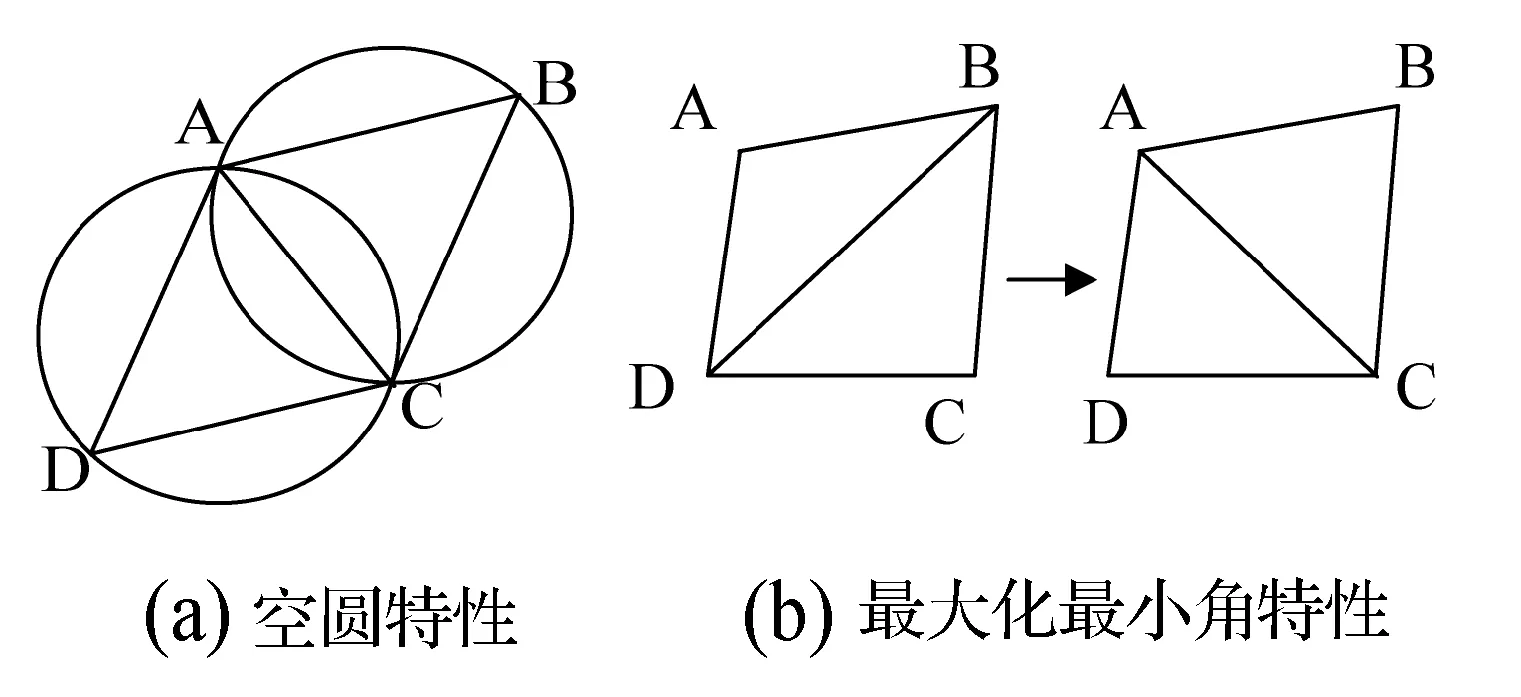
图1 Delaunay三角剖分中的两个重要特性
2 生长法

图2 生长法三角剖分流程图
生长法[12]是Delaunay三角剖分最直接的方法,算法设计直接由Delaunay三角剖分定义而来,算法简单明了。根据拓扑定义,Rn空间可由n维(及n维以下)单纯形组合构造,相邻两个单纯形的相交部分为n-1维面。生长法是以面为基础,在生长规则的控制下,为面加入顶点,构造新的单纯形。生长法三角剖分流程如图2所示。
传统的生长法[13,14]采用递归过程实现,Triangulation算法为递归生长法的C语言伪代码:
FunctionTriangulation(P,f0)/*P为输入点集,f0为输入单纯形面*/{
v = FindNextVertex(P,f0);
s = BuildSimplex(f0,v);
print(s);
//打印输出
for each f∈s
Triangulation(P,f);
}
Triangulation算法以一输入面f0为基础,使用FindNextVertex函数查找一个顶点v,使用f0和v构造单纯形s。接下来遍历s中的每个面f,重新调用Triangulation构造下一个单纯形。print语句打印输出新构建的单纯形,如果需要存贮输出,则只需设置一个列表,顺序存贮即可。
3 改进生长法
Triangulation算法是一个递归算法,容易理解和实现,但是大数据量计算的算法时域和空域特性差,因此需进行消去递归。据此,本文从数据结构上改进递归生长法,设计了一个(n-1)维面列表FList,用于动态存贮各面,从而消除递归。
3.1数据结构设计
数据结构设计上,队列能够实现顺序存取和快速查找,但是删除操作效率低。为了提高算法性能,尤其是实现随机位的快速搜索和删除操作,采用哈希表进行数据操作。常规哈希表中数据的存贮位是随机的,因此还必须设计顺序存贮的哈希表结构。本文使用C++标准库的list容器作为顺序存贮器,结合Boost库的非排序类容器unordered中的unordered_set哈希模板,构造顺序存贮的哈希表。
unordered_set
数据结构定义:
template
struct StruHashFunc
{
size_t operator()(Tp1) const
{
return pHashFunc(p1);
//hash_value函数以一个对象为参数
}
};
template
struct StruEqualFunc
{
bool operator()(Tp1,Tp2) const
{
return pEqualFunc(p1,p2);
//equal函数以两个对象为参数
}
};
typedef StruHashFunc
typedef StruEqualFunc
接下来,就可以自定义顺序哈希表。为了便于用户使用,以list为外部容器,用于输入输出。在数据结构内部使用hash容器存贮对象并生成对应key值,用于搜索定位,两者内部的读写操作要保证一致。如下为自定义接口IListedHash的过程:
1) 以对象类为模板参数定义该接口类:
ctemplate
2) 以TValue为list参数,定义list接口类:
typedef std::list
3) 定义哈希表接口类:
typedefboost::unordered_set;
4) 定义迭代器,其中hash迭代器为内部迭代器,list迭代器为外部迭代器:
typedef typenameI Hash::iteratoriterator_in;
typedef typename IList::iteratoriterator;
5) 定义内部数据存贮变量:
IListlistdata和IHash hashdata;
6) 定义与list类似的各项操作,主要有insert、find、erase等操作和begin、end等迭代器操作方法,在实现上保证listdata和hashdata数据的同步读写。
采用以上设计的哈希表进行数据操作,对Triangulation算法进行消去递归,改进后为Triangulation2算法。
Triangulation2算法的伪代码为:
FunctionTriangulation2(P,FList)
/*P为输入点集,FList为输入面列表*/
{
whileFList≠
{
f0 = ExtractHash(FList);
v = FindNextVertex(P,f0);
s = BuildSimplex(f0,v);print(s);
//打印输出
for each f∈s
UpdateHash(FList,f);
}
}
UpdateHash(FList,f)
{
if f∈FList
DeleteHash(FList,f);
else
InsertHash(FList,f);
}
上述代码表示中有三个哈希表的操作函数:ExtactHash、DeleteHash和InsertHash,它们分别对面列表执行读取、删除和插入操作,自定义UpdateHash函数对面进行更新操作。为了避免重复生长,读取f0的ExtractHash函数中包含了f0的DeleteHash操作。算法以面列表FList为输入,循环判断是否为空,每次循环从FList中读取一个面f0,构建单纯形s,遍历s中的每个面f,如果已存在于列表,则从FList中删除,否则,插入f0,算法直至FList为空时结束。
3.2三角剖分的详细过程
三角化算法的核心语句是FindNextVertex函数中满足Delaunay规则的点的搜索。为了叙述方便,本文给出如下两个定义:
定义1由多个三角形或者两条边界边完全封闭的点为死点;反之,未被完全封闭的点称为活点。
定义2相邻三角形的共有边或边界边为死边;其他边称为活边。
设点集为P,当前遍历面为边e(v0,v1),其中v0,v1∈P是e的两端点,以边e为基础,采用以下生长规则搜索第三点v2:
•只对邻域点进行搜索
此规则用于确定总体搜索范围。设点v0和v1的邻域分别为Neib0和Neib1,则搜索范围确定为Neib01=Neib0∪Neib1。
•只对活点进行搜索

图3 点和边的活性
在图3中,粗线边v5v7和边v7v8为已确定的边界边。以v0为端点的边,以及边v5v4、v4v7、v4v8均为死边,两条边界边v5v7、v7v8亦为死边,其他边均为活边。显然,死边是当前搜索状态下的内部边,不能作为基础边再行生长,需要从面列表FList中删除;相对应地,活边作为外部边,应作为生长边进入FList。
为了准确表述,用点或边的使用频次f表示点或边的活性。在构网过程中,一条边只能为边界边,或者为相邻两个三角形的共有边,因此边的活性取值范围为{0,1,2}。点的使用频次与其构边的次数有关,设与点v关联的边集为E∈FList,则f的计数规则是:如果E=∅,则置f=-1;否则f=E.size。由于E是FList的子集,因此f值和E的增减都在FList中体现:v的每次构边都将通过InsertHash加入FList,相应有f++;每次提取边构建三角形时都将使用ExtractHash从FList中删除边,相应有f--。
•生长点必须位于近邻三角形的右侧
此规则用于限定生长方向。为了定义三角形的生长方向,一般统一定义为逆时针(或顺时针)方向为三角面正向。这也延伸定义了构面边为有向边,其方向与面的方向一致。如图4所示,已构三角形面v0v1v2为逆时针方向,三条边v0v1、v1v2、v2v0亦为逆时针方向。此时,若对边v1v2搜索新的生长点,为了避免出现交叉三角形,必须限定生长点位于边v1v2的“右侧”。二维情形下,边v1v2将平面划分为左右两个半平面;三维空间中,假想经过边v1v2创建一个与三角面v0v1v2垂直的平面,该平面将整个空间划分为两个半空间,分别记为HS-和HS+。边v1v2是两个半空间的一条交界边,为了满足三角面方向统一的要求,在搜索空间HS+中,对边v1v2进行扩展时,应取其反向边v2v1。本规则限定了生长点必须位于HS+空间,该规则下,图3的备选点集{v3,v4,v5}中只有{v4,v5}为合法生长点集。

图4 半空间搜索
•限定三角形的最小角度Amin
此规则避免出现狭长三角形,用于满足Delaunay最大化最小角特性。推荐Amin=5°~30°。
•三角形外接圆半径与当前边的比值大于限定值Rmin
此规则用于外接圆半径,即缩小待建三角形的影响范围,旨在满足Delaunay空圆特性。
3.3基于微切平面的生长法
在三维点云空间中,对邻域点的搜索实际是基于四面体的空球搜索,搜索速度和精度以及编程难度比二维点云大。对此,考虑将三维空间降维至二维,将三维点投影至微切平面,在二维平面内构建三角形。之后通过空间点与投影点的映射关系将平面三角网映射回空间,从而实现三角形的空间构网。算法可简单描述为以下四个步骤:
1) 由当前遍历面为边e(v0,v1)的邻域Neib01=Neib0∪Neib1构建微切平面T,构造UV二维坐标系;



4 实例分析
采用C++语言编程在Microsoft visual studio 2008上实现以上算法,并且调用OpenGL库函数显示点云,实验所用的计算机配置为Intel Core 2.30 GHz CPU,1.19 GB内存。对汽车挡泥板、兔子、马鞍模型进行三角剖分,其点云数量分别是:6408、34 834、56 780个。为便于叙述,将Triangulation算法称为方法1,Triangulation2为方法2,基于微切平面的生长法为方法3。方法1、方法2三角剖分思路相同,不同的是数据结构操作以及递归过程。三种方法对三种模型的三角化结果和耗时比较如表1和图5-图7所示。图5-图7中(a)是点云模型,(b)是方法1、方法2三角剖分结果,(c)是方法3结果。从表1和图5-图7中得出,方法1-方法3的三角化结果相同,但从耗时比较上来看,方法2三角剖分速度比方法1快,尤其是当点云数据较大时,方法2耗时几乎是方法1的一半。此外,本文提出的基于微切平面的生长法即方法3耗时更小,与方法2相同数据结构实现方法3时耗时比传统的生长法(方法2)耗时更小,对大数据点云模型,本文的生长法三角剖分效率更高。
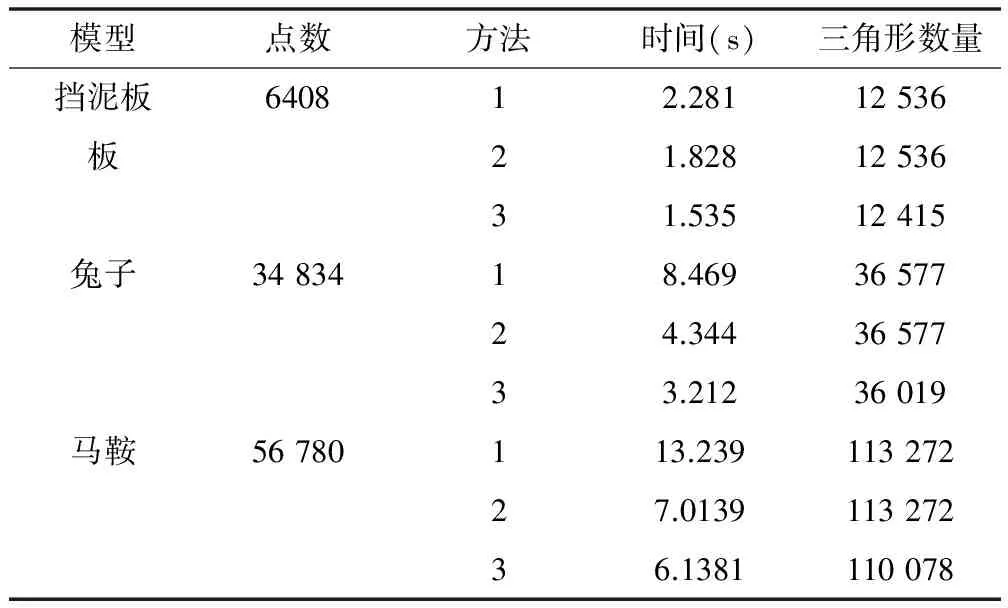
表1 3个模型的实验数据

图5 挡泥板模型三角化结果

图6 兔子模型三角化结果

图7 马鞍模型三角化结果
5 结 语
本文对Delaunay三角剖分算法中的生长法进行了详细的分析,设计了一种顺序存贮的Hash数据结构,实现临时单纯形对象的快速存取、插入和删除等操作,采用Hash数据结构消去递归的生长法执行时间更短。此外,本文提出了基于微切平面的生长法,将基于空间四面体的空球搜索降维至局部二维的空圆搜索,同样采用Hash数据结构对基于微切平面法的生长法进行操作。微切平面生长法三角剖分效果与传统方法效果相同,但微切平面生长法速度更快。对数据量为30 KB的兔子模型,三种方法的计算时间分别是8.5、4.3、3.2 s。
[1] Digne J,Cohen-Steiner D,Alliez P,et al.Feature-preserving surface reconstruction and simplification from defect-laden point sets[J].Journal of Mathematical Imaging and Vision,2014,48(2):369-382.
[2] Lhuillier M.2-Manifold Tests for 3D Delaunay Triangulation-Based Surface Reconstruction[J].Journal of Mathematical Imaging and Vision,2014,51(1):98-105.
[3] Gong W,Liu Y J,Tang K,et al.Approximate Delaunay mesh reconstruction and quality estimation from point samples[J].Journal of Computational and Applied Mathematics,2015,274(15):23-34.
[4] Gálvez A,Iglesias A.Particle swarm optimization for non-uniform rational B-spline surface reconstruction from clouds of 3D data points[J].Information Sciences,2012,192(1):174-192.
[5] Boissonnat J D.Geometric structures for three-dimensional shape representation[J].ACM Transactions on Graphics (TOG),1984,3(4):266-286.
[6] Edelsbrunner H,Mücke E P.Three-dimensional alpha shapes[J].ACM Transactions on Graphics (TOG),1994,13(1):43-72.
[7] Coakley E S,Rokhlin V.A fast divide-and-conquer algorithm for computing the spectra of real symmetric tridiagonal matrices[J].Applied and Computational Harmonic Analysis,2013,34(3):379-414.
[8] Xu Y,Liu L,Gotsman C,et al.Capacity-constrained Delaunay triangulation for point distributions[J].Computers & Graphics,2011,35(3):510-516.
[9] Carr J C,Beatson R K,Cherrie J B,et al.Reconstruction and representation of 3D objects with radial basis functions[C]//Proceedings of the 28th annual conference on Computer graphics and interactive techniques,2001:67-76.
[10] 赵建东,康宝生,康健超,等.改进的基于径向基函数的曲面重建算法[J].西北大学学报:自然科学版,2012,42(5):744-748.
[11] 方林聪,汪国昭.基于径向基函数的曲面重建算法[J].浙江大学学报:工学版,2010,44(4):728-731.
[12] 余杰,吕品,郑昌文.Delaunay 三角网构建方法比较研究[J].中国图象图形学报,2010,15(8):1158-1167.
[13] 袁舒,杨烜.基于 Delaunay 三角网生长法的并行图像插值方法[J].计算机应用与软件,2012,29(3):62-68.
[14] 孟宪海,成文迪,徐博,等.基于 Voronoi 取小邻近点集的 Delaunay 三角化方法[J].图学学报,2013,34(6):36-41.
IMPROVEMENT AND COMPARATIVE ANALYSIS OF DELAUNAY TRIANGULATION ALGORITHM
Yuan XiaocuiWu LushenChen Huawei
(School of Mechanical and Electrical Engineering,Nanchang University,Nanchang 330031,Jiangxi,China)
Aiming at the problem of computation speed of Delaunay algorithm,we improved it from two aspects of data structure and algorithm.After analysing the algebraic topology of Delaunay triangulation,we designed a sequentially stored Hash data structure so that the temporary simplex object can be accessed,queried,inserted and deleted rapidly and in order.We took the activity analysis of edge object of simplex as the core,and employed Hash data structure to operate the recursion process of incremental algorithm removal.Besides we proposed the micro-tangent plane-based incremental algorithm,which decreases the dimension of the space tetrahedron-based blank sphere searching to local two-dimension blank circle searching.The triangulation experiments were carried out on car fender and bunny model,experimental results demonstrated that the triangulation results of recursion-removed and micro-tangent plane-based Incremental algorithms were the same as that of traditional Incremental algorithm,but the computation speed was higher than the traditional method.
Delaunay triangulationIncremental algorithmHalf spaceImplicit surface
2015-04-22。国家自然科学基金项目(51365037,51065021)。袁小翠,博士生,主研领域:逆向工程与数字图像处理。吴禄慎,教授。陈华伟,讲师。
TP391
A
10.3969/j.issn.1000-386x.2016.09.039
