基于混合遗传算法的高维离群数据检测

施冬冬，方星星

（1.安徽大学江淮学院，安徽　合肥　230039；2.解放军陆军军官学院，安徽　合肥　230000）

基于混合遗传算法的高维离群数据检测

施冬冬1，方星星2

（1.安徽大学江淮学院，安徽合肥230039；2.解放军陆军军官学院，安徽合肥230000）

离群点研究在实际应用中有着重要的意义，随着数据规模的不断扩大，传统的离群点检测方法已经不适用于高维空间数据，本文在遗传算法的基础上结合模拟退火算法，一方面利用遗传算法对高维数据处理有很好的全局搜索能力，一方面利用模拟退火算法的局部搜索能力，最后经实验证明，本文提出的新算法能有效的提高高维空间离群点检测的效率.

离群点；遗传算法；模拟退火算法

1　问题描述

离群点检测是数据挖掘的重要内容之一.目前离群数据检测的研究十分活跃，已经有许多离群数据挖掘算法，其主要方法可归为五类，即基于聚类的方法：通过聚类发现常规模式，不属于任何一个类的数据即是离群点；基于统计的方法：离群点是那些偏离正常分布（如正态分布、Poisson分布等）的数据，这类方法需要数据服从一定的分布［1］；基于深度的方法：计算d维凸球的不同层，那些位于球最外层的数据为离群点，这种方法在大型高维数据中的应用较为困难；基于距离的方法：给定数据集X及距离dmin，对于点p∈X，若至少存在X中的m个数据点到点p的距离大于dmin，则称p为离群点；基于密度的方法：如果一个数据点的局部离群因子高于一个阀值则被认为是一个离群点，它用于发现局部离群点［2］.

目前，低维离群数据的检测算法已较成熟，受“维度灾”（the curse of dimensionality）的影响，许多传统的检测算法运用到高维数据上往往失效，但是在实际生产应用中，高维数据普遍存在，例如，基因表达数据、金融数据、多媒体数据以及文本数据等［3］.因此对高维数据离群点检测算法的研究具有非常重要的意义.遗传算法对高维空间的数据处理有很好的全局搜索能力，但是缺点是显而易见的，局部寻优能力差，容易产生“早熟”现象（局部收敛）［4］.模拟退火算法有很强的局部搜索能力，本文在遗传算法基础上结合了模拟退火算法，能使搜索过程避免陷入局部收敛.

2　高维空间离群数据描述

我们把一组高维空间数据用规模为n的横向量集合A表示，每个向量维数是k，表示成A=｛a1，a2……an｝，其中ai=｛ai1，ai2……ait｝，k维数据的每个属性划分为f=1/φi等份，φ为第i维被划分的间隔个数，设maxi和mini分别表示数据集n在第i维上的最大值和最小值，那么划分的每个间隔的长度即为：对于一个s维的网格，s＜k，即k维数据投影到s个不同的维上.假设各个分量的取值是独立的，那么一个点在s维的网格中是否出现可以用Bemoulli随即变量来描述，约为fS.n为数据的总数，在s维的空间中，期望值为n·fS，标准方差为，设s维网格H中数据的实际个数为n'，那么H的稀疏系数

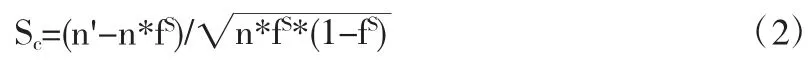
如果Sc取负值，即认为H中的数据点个数明显少于期望值.实际上，大多数时候数据分量的取值并不是统计独立的，也并不总呈均匀分布.然而，稀疏系数仍然可以正确衡量空间中数据的稀疏程度.我们的目标是寻找具有最小稀疏系数的s维子空间.

3　遗传算法（GA）及其改进

3.1染色体编码

染色体的长度为数据集的维数.对于一个n维数据集，第k（k≤n）个属性的取值可能为1～φ或者“*”，“*”表示对该属性的取值不关心.例如对一个四维数据集的二维子空间它的一个可能的二维子空间模式为“*3*9”，这个模式中，第二维和第四维的取值是确定的，而第一维和第三维的取值是不关心的.

3.2适应度函数

Sc为稀疏系数即（2）式，适应度与稀疏系数正好相反，适应度越大，子空间中的数据越少.

3.3模拟退火算法

传统的遗传算法在进行选择、交叉和变异的过程中一般采用轮盘赌的方式，选择、保留上代最优染色体替换下一代最差染色体的方式，但是选择个体概率和个体适应度成正比，导致前期有的个体充斥整个种群，而后期个体之前没什么差异，会出现“早熟”现象.在这里我们利用模拟退火算法的思想，对个体适应度随时间改变进行进化.公式如下：

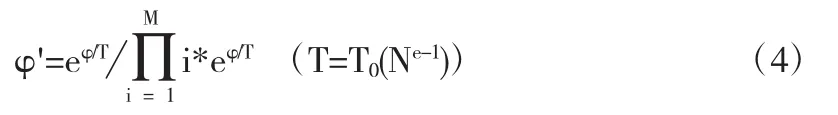
这里e为遗传算法中的世代数，M为种群数，φ为改变前的适应度，φ'为改变后的适应度，T0为设置好的初始温度，我们把他设置为200，N是一个无限接近1的一个小数可以根据实际来改变（这里我们设为0.9999）.这样我们在每次使用轮盘赌选择时，可以随机选择由公式3得到的适应度，从而保证前期适应度打的个体会缩小差距，并且避免后期出现个体之前适应度差距很小，可以适当的放大适应度，确保了改进后的适应度能自适应的进行伸缩，有效的缓解了之前我们提到的遗传算法“早熟”现象.

3.4染色体交叉

常用的交叉方法为两点交叉，即任选一点作为交叉点并交换这点右边的部分.但是这种两点交叉有时会产生不合理的结果.我们对交叉方法作了一定的修改，来保证父串和子串都对应相同给定维数的子空间模式.令k为指定的子空间维数，对于一对模式阶为k的字符串st1和st2，指定串中的一个位置，有以下3种类型：

（1）在此位置上，两个串都是*

（2）在此位置上，两个串都不是*

（3）在此位置上，两个串中只有一个是*

设st为st1和st2交叉生成的一个子串，很明显在第一类位置上，子串st也是*.假设st1和st2含k'个第2类位置，则st1和st2均含有k-k'个第3类位置，两者总共包含2（k-k'）个第3类位置.字符串st1和st2交叉过程描述如下：

①设R为第二类位置的集合（k'个），Q为第三类位置的集合，s为一子串.

②枚举第二类位置的所有可能重组方式（2k'种），选择稀疏系数最小的一种组合方式设置在s的对应位置上.

③反复选取Q中第三类位置对应的父串值并设置在s的相应位置上，使得s有最小的稀疏系数，直到s的k个位置都设置完毕.s的其它位置设为*.

④令s'为s的补串，s'的每一位置的取值相对于s来自不同的父串，将s'作为s1和s2交叉后的另一个子串.很显然，重组后的交叉过程能够保证子串s和s'与父串有相同的维（阶）数.

3.5染色体变异

变异的目的是改善遗传的局部搜索能力，维持群体的多样性，防止出现早熟现象.这里使用如下变异方法：首先在得到的两个新个体和上，以概率Pm随机选择在st1和st2上的某一维非*属性qi，i∈［1，k］，然后交换染色体st1和st2在qi属性上的编码.

3.6算法步骤

本文的算法步骤的具体流程为：

4　实验结果及分析

本文在VC6.0开发环境下进行验证，实验采用UCI机器学习仓库的数据集（Breastcancer）.PC机的配置：AMD Athlon（tm）II X2 245，DDR2 2G内存.数据集包含100000个样本数据，其中150个离群点，交叉概率设为69%，变异概率为0.1%，初始温度T0定为200，温度冷却系数α=0.99.我们选取不同规模的样本数据采用本算法进行比较，如表1所示.

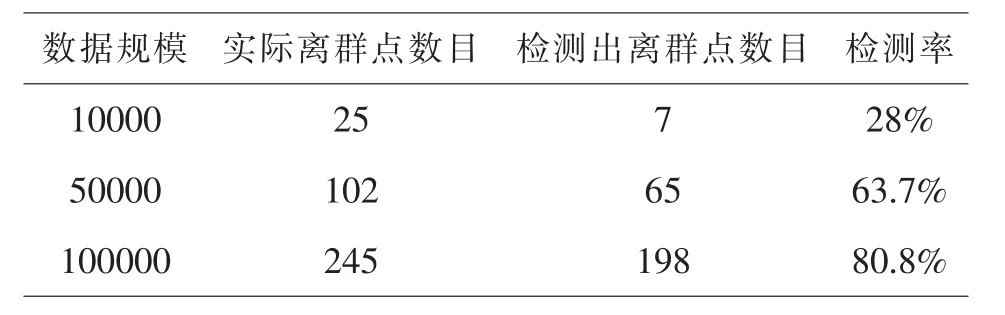
表1

可以发现随着数据规模的扩大，正确离群点检测的概率越高.

为体现出本算法的优越性，先将该算法与一般遗传算法的检索结果进行对比，如表2所示：

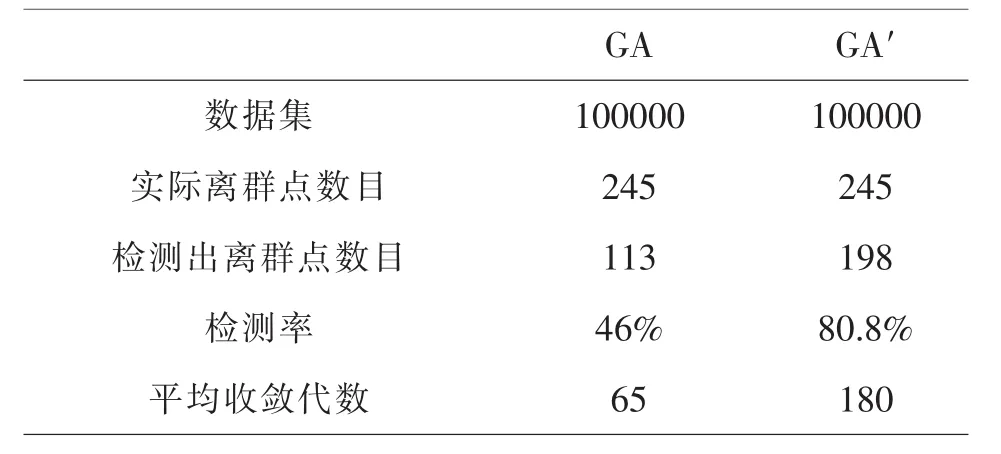
表2

从表2看出，在相同的情况下，GA'检测率最高，表明该改进算法具有优于一般遗传算法的性能；GA'平均收敛世代数明显大于前者，也说明混合了模拟退火伸缩适应度的遗传算法的确可以有效地缓解“早熟”、过早收敛的现象.

5　总结

本文在遗传算法的基础上结合模拟退火算法的局部搜索能力，有效的避免了遗传算法容易“早熟”的特点，并且，通过实验证明新算法的有效性.但是在数据规模较小的情况小，该算法对离群点检测的效率还有待提高，这也是以后对该算法进一步改进的地方.

〔1〕Aggarwal C，Yu P.An effective and efficient algorithm for highdimensional outlier detection［J］.The VLDB Journal，2005，14（2）：211-221.

〔2〕Charu C.Aggarwal，Philip S.Yu.Outlier Detection for High Dimensional Data ACM2001.

〔3〕AgrawalR，Gehrke J，Gunopulos D，et a1．Automatic Subspace Clustering of High Dimensional Data for Data Mining Applications［A］．Haas L M，Tiwary A．Proc．ofthe ACM SIGMOD InternationalConferenceonManagement of Data［C］．Seattle：ACM Press，1998．94．105．

〔4〕范明，孟晓峰.Jia Wei HAN and KAMBER M.Data mining concepts and techniques［M］.北京：机械工业出版社，2007.

O212；TP311.13

A

1673-260X（2016）10-0001-02

2016-06-16

安徽省省级自然科学研究一般项目（无编号）