室内配电房混凝土地板的振动功率流场分析
2016-11-09徐禄文高芳清邹岸新
徐禄文,梁 林,高芳清,吴 祺,邹岸新
(1.国网重庆市电力公司电力科学研究院,重庆 401123;2.西南交通大学 力学与工程学院,成都 610031)
室内配电房混凝土地板的振动功率流场分析
徐禄文1,梁林2,高芳清2,吴祺2,邹岸新1
(1.国网重庆市电力公司电力科学研究院,重庆 401123;2.西南交通大学 力学与工程学院,成都 610031)
室内变压器常安置于混凝土地板,运行时会引起地板振动并向外传播。以地板与四周边界固结并考虑地基的弹性,建立混凝土地板的振动分析模型,基于Hamilton方程及振型叠加法对地板的振动位移方程进行详细推导与求解。在此基础上,利用功率流方法对地板振动传播特性进行研究分析,得到变压器典型激振频率下地板的振动功率流传递特性与衰减情况;最后利用有限元法对地板进行谐响应分析,得到混凝土地板的振动功率流场分布图,并对不同激振频率下的振动功率流场进行比较与分析。
振动与波;变压器;混凝土地板;振动功率流;谐响应分析
室内配变房的变压器置于混凝土地板上,变压器运转激起混凝土地板的振动,板振动会产生振动能量的传递,通过混凝土地板将能量传递至墙体以及相邻居室乃至各个房间,因为振动而产生的结构声会大大影响人们的日常生活,因此弄清振动在混凝土板内的传播特性与规律非常必要[1-3]。考虑到混凝土地板下地基的弹性支撑作用,本文对混凝土板置于弹性地基上的受迫振动进行分析,对于板的受迫振动,许多学者已进行过大量的工作,也取得了丰硕的研究成果[4-6]。目前常用的研究方法,大体上分数值方法和能量方法,数值方法主要包括有限元法(FEM)[7-8]、边界元法(BEM)[9-10],其中有限元法对于高频分析存在着相对较大误差,能量法对于位移函数的选取又比较困难。考虑到二者的局限性并结合混凝土板置于弹性地基上,本文建立了混凝土板置于弹性地基上的力学模型,该模型严格按照弹性地基的动力刚度特性对弹性地基进行了力学简化,得到了弹性地基的竖向抗压刚度动力解,在此模型基础之上结合Hamilton原理建立方程,并详细地对变分方程进行推导求解,得到混凝土板置于弹性地基上的振动微分方程,再利用振型叠加法又对位移方程的解析解进行详细的推导和求解,在求得的位移方程基础上对混凝土板的振动功率流传递特性进行分析,得到了在4种变压器运行的典型激振频率下混凝土板内振动功率流的传递特性[11-15]。最后通过有限元方法对混凝土板进行谐响应分析,得到了变压器不同激励频率下的功率流场分布图,这些功率流场图能够很直观的显示振动功率流在混凝土板内的传递与分布状态。
1 四边固支混凝土地板在弹性地基上的理论模型
如图1所示。将变压器在混凝土板上激振情况简化为如下板结构分析模型,变压器振动简化为集中简谐激振力P(t),配电房混凝土地板与四面墙体固结,因此考虑混凝土板的边界条件为四边固支情况。又考虑到板置于弹性地基上,将地基简化为刚度为K0的弹簧,不考虑弹性地基阻尼,K0为地基竖向刚度系数动力解,与地基土的力学参数有关,计算式取
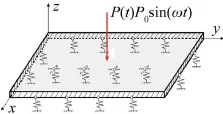
图1 混凝土板简化结构示意图
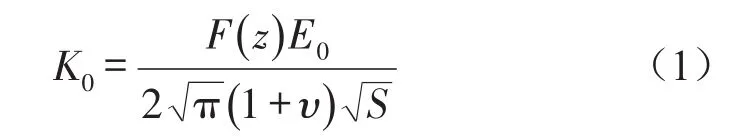
混凝土板在变压器激励下振动,设板振动的总势能为V,地基的弹性势能为V0,T表示混凝土板振动时的总动能,W表示外力做功,其与位移的关系表达式如下
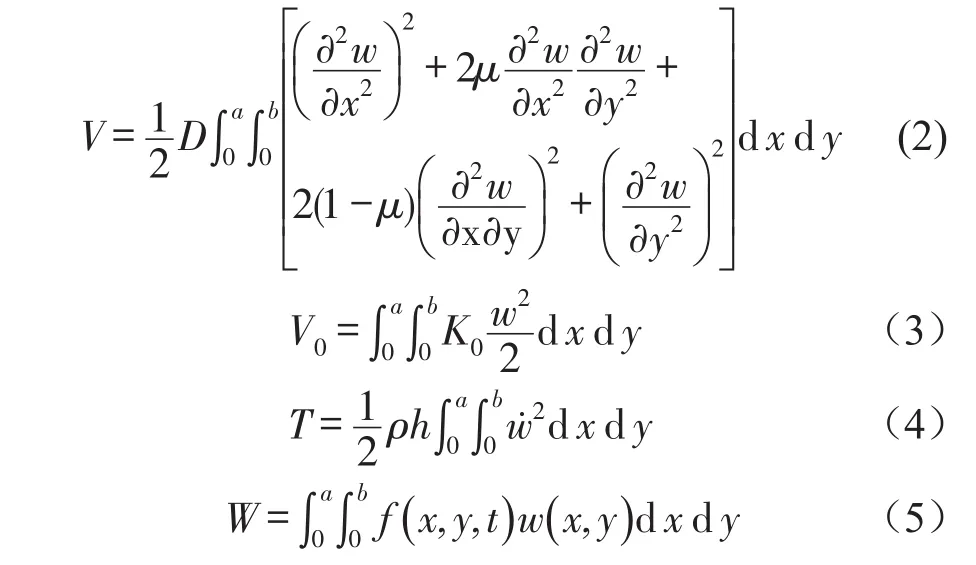
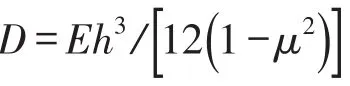
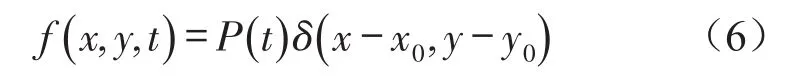
2 混凝土板的Hamiltonilton方程及位移函数
2.1混凝土板的Hamilton方程
由弹性力学知,混凝土板的Hamilton方程为
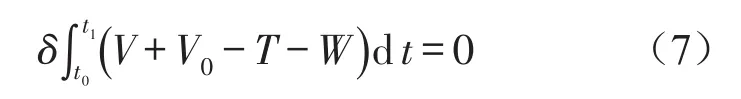
通过哈密顿方程可对位移函数进行求解,将式(2)-式(5)代入式(6)并对各项式子分别求变分可得

2.2混凝土板位移函数的求解
对式(12)采用振型叠加法,将混凝土板的位移方程按正则振型Wi,j展开成如下的级数
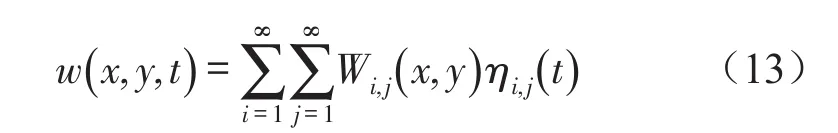
其中ηi,j(t)为主坐标,将上式代入式(12)求出的振动微分方程中可得
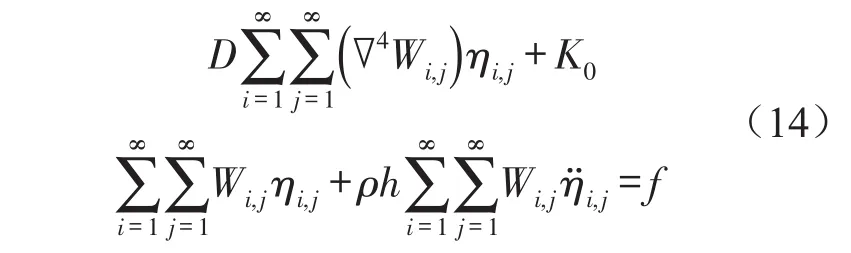
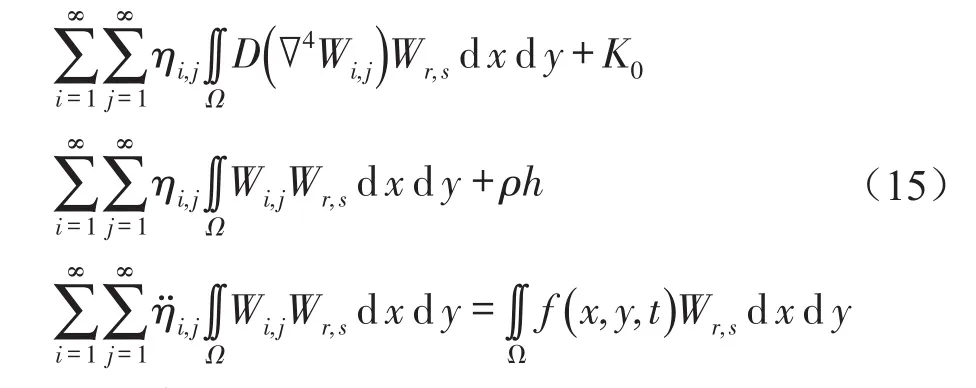
由主振型之间的正交性条件,上式可化简为
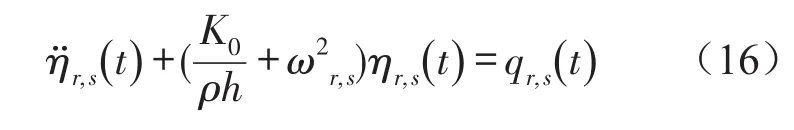
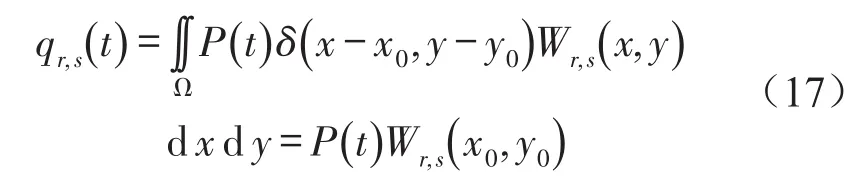
通过该方程便可解得主坐标ηi,j(t)的方程。
对于Wi,j(x,y)可通过有限积分变换,得
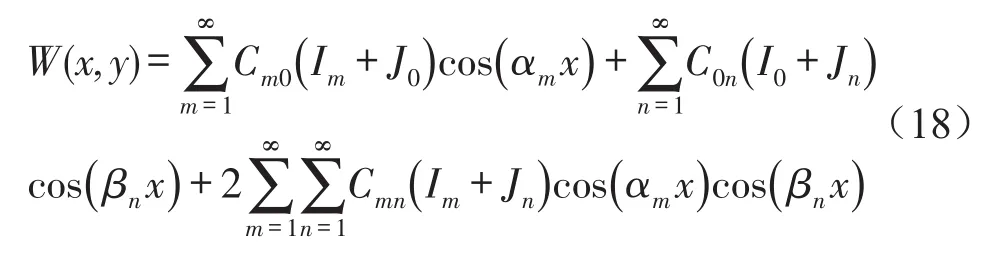
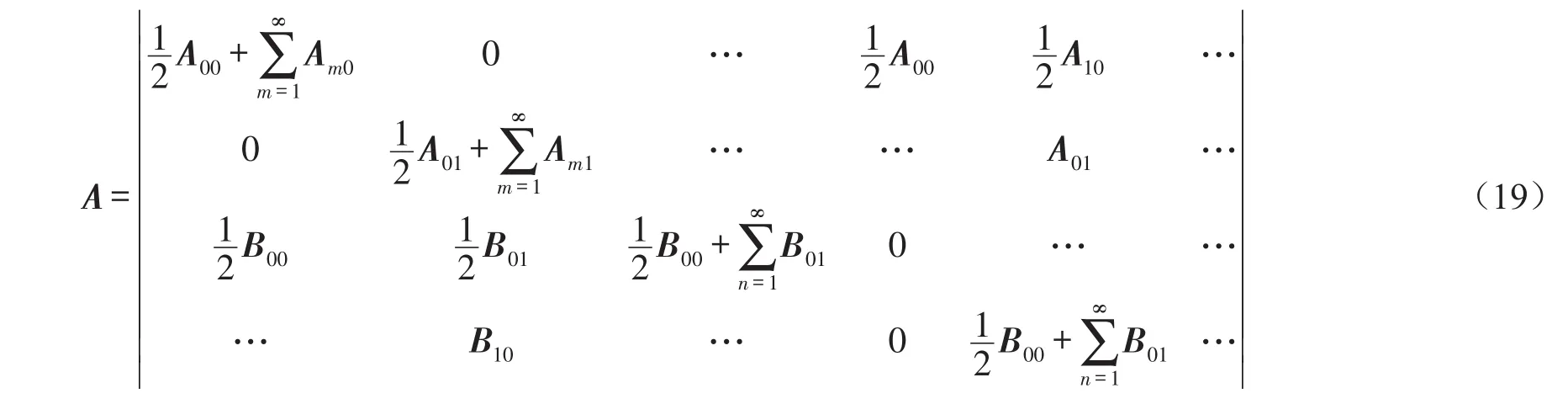

3 混凝土板的导纳功率流分析
经上述分析模型中混凝土地板位移方程的确立与推导,可得到位移方程的解析解,并可对不同点的位移、速度或者加速度响应进行定量分析。基于较为全貌性地反映地板振动传递过程以及衰减情况的考虑,这里采用导纳功率流法,通过能量分析描述地板振动的传播状态。
结构的导纳能够很好地反应结构对输入的动力响应特性,这里对地板的速度导纳进行分析。基于前述对混凝土地板位移方程的推导与求解,设输入激励的激振频率为ω,则速度导纳的表达式如下
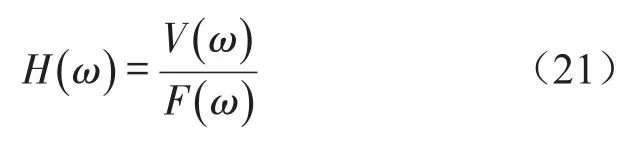
式中V表示激振速度,F表示激振力。
导纳功率流具有较高的预测精度,它把系统的响应和激励统一到功率流概念中,不仅给出振动能量传输的一种绝对量度,还给出了振动能量的传播特性,便于从能量的角度清晰地了解能量在结构中的传播,从而对振动和噪声进行有效的控制。
同时功率流包含力与速度的幅值以及它们之间的相位关系,避免单纯使用速度有效值表示的振级落差带来的一些问题。且功率流反映了振动能量的传递,可获得系统中的能量传递规律,设混凝土板结构中任一点的功率流强度为I(x,y)
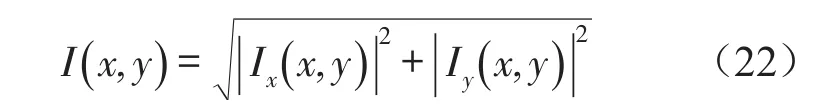
式中Ix(x,y)和Iy(x,y)分别表示I(x,y)沿x轴和y轴的分量,大小为
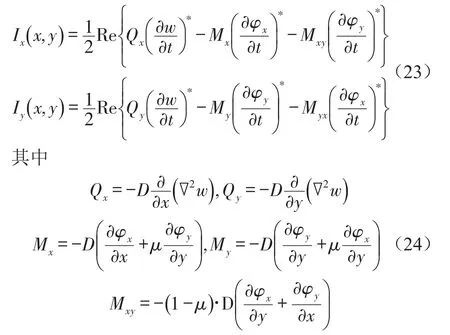
4 数值计算
某变压器置于室内配电房混凝土地板上,其运转时的激振频率ω取50 Hz两倍之倍频,通过对配电房地板的信号检测,得到配电房地板的加速度时程曲线及频谱图如图2所示。
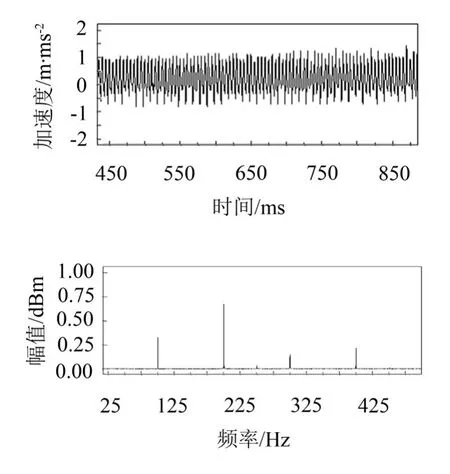
图2 配电房地板加速度时程曲线及频谱图
这里以100 Hz、200 Hz、300 Hz、400 Hz作为计算频率,变压器置于混凝土板中心激振,混凝土板长为a=5 m,宽为b=5 m,厚度为h=0.1 m,板的密度ρ=3 000 kg/m3,弹性模量 E=300 GPa,泊松比μ=0.2,弹性地基的刚度系数K0=5 MPa/mm。
本例中,激振力对称和混凝土板尺寸的几何对称,理论上讲在混凝土板内关于激振点中心对称的任意两点的响应情况也是完全相同的。如图3所示,该图为关于激振点(2.5 m,2.5 m)中心对称的两点A(2 m,2 m)(图3(a)和B(3 m,3 m)(图3(b)的速度导纳曲线图,其中(红色)实线为通过本文方法推导计算的导纳-频率曲线图,(蓝色)虚线为有限元方法的计算结果。结果表明计算结果与理论分析一致,同时采用本文方法与有限元的计算结果亦具有一致性。
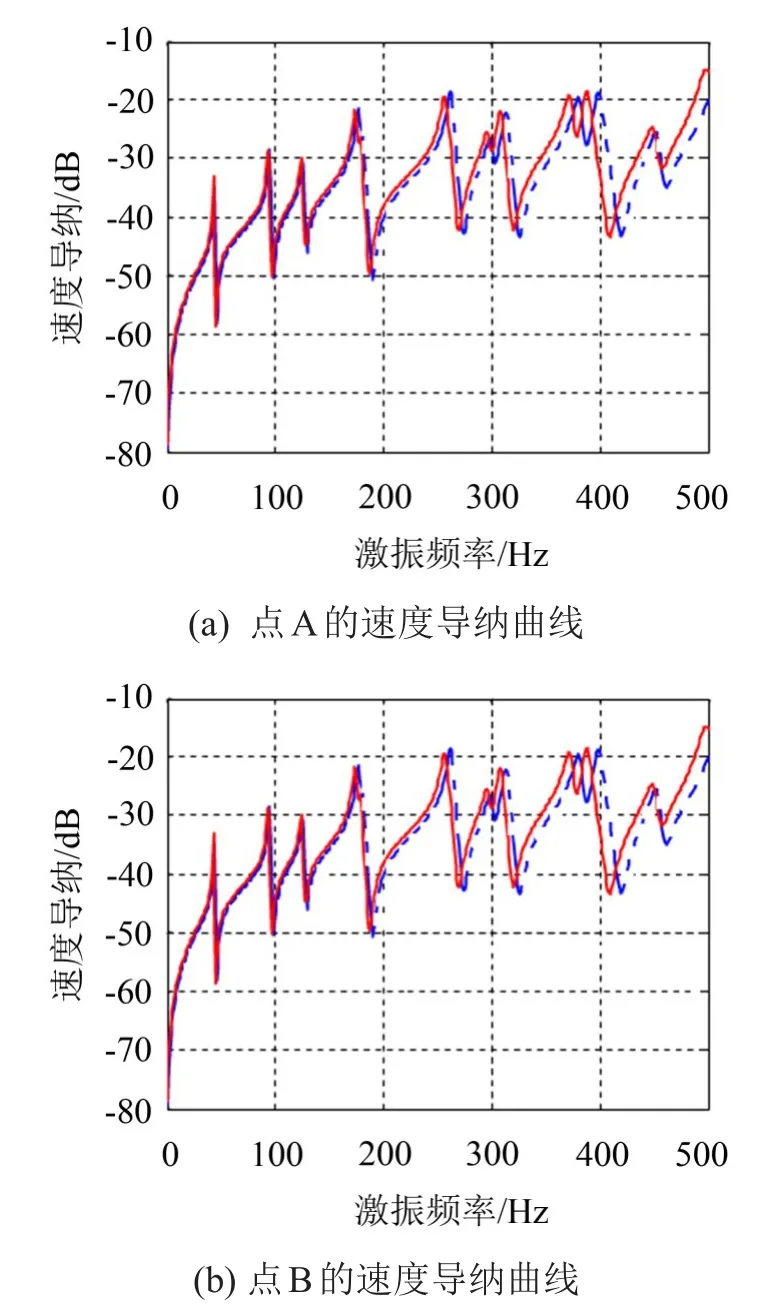
图3 点A和B的速度导纳曲线
另外从图中还可看出,在低频阶段两曲线是基本完全吻合的,但随着频率的逐渐升高,两条曲线产生了相对的偏移,产生这一现象主要是因为有限元方法对于高频的计算精度下降,要达到更高的精度,就需要对单元进行更细更密的划分。
从图2可知,变压器激起混凝土板振动的典型频率主要为100 Hz、200 Hz、300 Hz、400 Hz,因此为了解变压器在典型激励频率下振动功率流在地板内的分布与传递衰减情况,这里采用有限元法对混凝土地板的振动功率流场进行了计算分析。其中单元采用solid-concret 65,网格划分为0.01×0.01 m。得到振动功率流场在混凝土地板的分布状态分别如图4(a)-图4(d)所示。
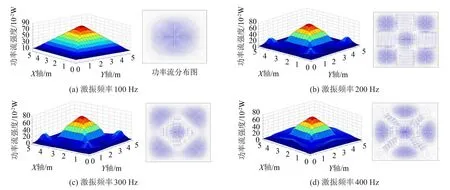
图4 不同激振频率下功率流传递分布图
从图4可清晰看出随着激振频率的增加,振动功率流的分布并不是按照如图4(a)(100 Hz激励)那样从大到小的向外扩散,而是随着激振频率的增加使得某些区域能量衰减,而有些区域形成能量的堆积,从图4(b)(200 Hz激励)可以看出功率流主要向靠近墙角的地方传递,因而在墙角处形成了能量的堆积,图4(c)(300 Hz激励)可以看到,功率流逐渐从墙角向地板的四边扩散传递,到最后的图4(d)(400 Hz激励)可看到功率流集中在地板的四边并堆积。
5 结语
本文针对室内配变房变压器振动引起与之接触混凝土地板的振动传递特性进行研究分析。
(1)依据室内变压器的实际安置环境建立了混凝土地板的力学分析模型,并通过Hamilton方程及振型叠加法对地板的位移方程进行了详细推导与求解,由此可对地板的导纳功率流进行定量分析并有诸多优点。
(2)以本文方法与有限元法分别对地板某点导纳功率流进行了计算,两者结果具有良好的一致性,且有限元在高频段计算精度下降。表明本文方法能够对地板的振动性态及传递情况进行有效分析。
(3)基于文中所述有限元模型对地板在变压器典型频率激励下的振动功率流场进行了计算与分析,得到了变压器4种典型激振频率下地板的振动功率流场分布图,为振动功率流在地板中的传播以及后续的结构传声研究奠定基础与提供参考。
[1]GIBBS B M,COOKSON R,QI N.Vibration activity and mobility of structure-borne sound sources by a reception plate method[J].Applied Acoustics,2008;123(6):209-4199.
[2]SPÄH M M,GIBBS B M.Reception plate method for characteristicofstructure-bornesoundsourcesin buildings:assumptionsandapplication[J].Applied Acoustics,2008,70:8-361.
[3]EN 15657-1:2007,Acoustic properties of building elements and of buildings-Laboratory measurement of airborneandstructurebornesoundfrombuilding equipment-Part 1:Simplified cases where the equipment mobility are much higher than the receiver mobility,takingwhirlpoolbathsasanexample.European Committee of Standardization,Brussels,Belgium,2007:2-3.
[4]姚伟岸,蔡智宇,胡小飞.矩形正交各向异性薄板弯曲受迫振动问题的分析解[J].动力学与控制学报,2011(1):12-17.
[5]MUKHERJEE M.Forced vertical vibrations of an elastic elliptic plate on an elastic half space a direct approach using orthogonal polynom-ials[J].International Journal of Solids and Structures,2001,38:389-399.
[6]LIM C W,LU C F,XIANG Y,et al.Onthenew symplectic elasticity approach for exact freevibration solutions of rectangular Kirchhoff plates[J].International Journal of Engineering Science,2009(01):131-140.
[7]吴鸿庆,任侠.结构有限元分析[M].北京:中国铁道出版社.2000:321-424.
[8]陈伟,何飞.基于结构参数化的有限元分析方法[J].机械科学与技术,2003(06):945-950.
[9]杨德全,赵忠生.边界元理论及应用[M].北京:北京理工大学出版社,2002:1-317.
[10]JASWON M A,MAITI M.An integral equation of plate bendingproblems[J].JournalofEngineering Mathematics,1968(1):83-93.
[11]IVARSSON L H,SANDERSON M A.MIMO Technique forSimultaneousMeasurementoftranslationaland rotational mobilities[J].Applied Acoustics,2000(61):345-370.
[12]曾勤谦,华宏星,韩祖舜.耦合结构中的功率流有限元法[J].上海交通大学学报,2000,34(4):5-503.
[13]仪垂杰,陈天宁,李伟,等.BBD板结构的振动功率流研究[J].力学学报,1995,27(4):495-500.
[14]冯国平,黄修长,刘兴天,等.基于振动功率流的船艉传递路径分析[J].噪声与振动控制,2010,30(2):2-5.
[15]吴大德,王立兵,王宇宁.基于机-电相似性的隔振系统功率流计算与分析[J].噪声与振动控制,2011,31(2):2-3.
Vibration Power FlowAnalysis of Concrete Floor of Indoor Transformers
XU Lu-wen1,LIANGLin2,GAO Fang-qing2,WUQi2,ZOU An-xin1
(1.Electric Power Science Research Institute of State Grid Chongqing Electric Power Company,Chongqing 401123,China;2.School of Mechanics and Eng.,Southwest Jiaotong Uni.,Chengdu 610031,China)
The indoor transformer is usually settled on the concrete floor.Operation of the transformer can induce the floor vibration which will spread outward.In this paper,the concrete floor is considered as a plate on an elastic foundation with its edges fixed.Then,the vibration analysis model of the floor is established.The vibration displacement function of the floor is derived and solved in detail based on the Hamilton equation and modal superposition method.On this basis,the propagation characteristics of the floor are studied using the vibration power flow method.The transmission and attenuation characteristics of the vibration power flow of the floor are obtained under the typical exciting frequency of the transformer. Finally,the harmonic response of the concrete floor is analyzed by means of the finite element method.The distribution diagram of the vibration power flow field of the concrete floor is plotted.The vibration power flow fields for the different exciting frequencies of the transformer are compared and analyzed.
vibration and wave;transformer;concrete floor;vibration power flow;harmonic response analysis
O422.6
ADOI编码:10.3969/j.issn.1006-1335.2016.05.027
1006-1355(2016)05-0128-05
2016-04-19
国网重庆电力公司科学技术研究资助项目(2014H01580)
徐禄文(1968-),男,四川广安人,高级工程师,主要从事电网电磁环境与噪声振动控制相关研究。E-mail:xuluwen023@qq.com
