基于半车解耦的半主动悬架模糊滑模控制

赵　强，张　娜

（东北林业大学 交通学院，哈尔滨 150040）

基于半车解耦的半主动悬架模糊滑模控制

赵强，张娜

（东北林业大学 交通学院，哈尔滨 150040）

为提高车辆的舒适度，提出基于半车解耦模型的半主动座椅悬架的模糊滑模控制。建立并分析半车悬架系统的动力学模型，通过将其等效变换为两组标准的动力学方程，实现把半车悬架系统解耦成四分之一车悬架系统。基于解耦后的四分之一车悬架系统对含四分之一车的座椅悬架设计模糊滑模控制策略:把天棚阻尼系统作为参考模型，将实际被控系统和参考模型间的动态误差引入到滑动模态中，通过切换函数及其导数的模糊化处理，来抑制滑动模态中抖振现象。并通过比较磁流变阻尼器输出力和模糊滑模控制器（Fuzzy Sliding Mode Controller）解出的期望力的差值，来确定提供给磁流变阻尼器的电压。最后通过与PID、滑模（Sliding Mode Controller）和被动悬架仿真结果的对比，验证该方法对半车座椅悬架系统减振效果具有明显的改善作用。提出的控制方法对于半主动悬架的实际控制具有参考价值。

振动与波；半主动悬架；半车解耦；磁流变阻尼器；模糊滑模控制器

汽车技术的发展进化和汽车市场的激烈竞争对乘坐舒适性、操控稳定性、行驶安全性等提出了更高的要求。车辆座椅悬架系统是一个多自由度振动系统，而振动是乘坐舒适性和行驶平顺性的主要因素，然而在各类悬架中，半主动悬架能耗小、结构简单、控制性能好，因而具有广泛的应用价值［1］。尽管“四分之一”车辆悬架的控制算法己经相对成熟，然而针对实际车辆，均具有多组悬架系统，它们之间相互耦合，将已有成熟的“四分之一”悬架系统控制策略简单移植并不能满足控制要求，此外，如果同时把多组悬架作为被控对象，系统变量将会增加，从而导致计算复杂度增加，控制实时性不高，因而难以投入实际应用。吴龙等对六自由度半车悬架系统进行解耦，提高了半车悬架系统性能，但是其解耦方法假设条件多、推导较复杂，仅实现了理论上的近似解耦［2］。董小闽等在提出的可控半主动悬架分姿态协调仿人智能控制方法中所用的方法对于八种运动姿态下存在的一种或多种运动耦合需要分别计算，同时需要预先定性分析车身姿态，因此该解耦控制方法实时性不理想，在实际车辆中实现较难［8］。本文以四自由度半车悬架系统为研究对象，经过理论推导，定量地求得传统的半车悬架系统中前、后子悬架系统之间存在的耦合力；进而提出通过非簧载可控阻尼器提供确定大小的阻尼力消除耦合力的假设，设计了采用双可控阻尼器的新型半主动悬架结构。

滑模变结构控制是一种典型的非线性控制算法，该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动，即所谓的“滑动模态”或“滑模”运动［4］。文献［5］设计了针对车辆电流变悬架系统的新型模糊滑模控制器并验证了该控制器的有效性［5］。文献［6］分别在时域和频域范围分析了其减振效果［6］。郑玲研究了汽车半主动悬架的模型参考滑模控制，取得了较好的效果［7］。模糊控制属于闭环反馈控制系统，主要缺点为控制精度差，稳定性分析比较困难，但适用于被控参数无法精确表示及参数之间无精确关系的系统［8］。本文利用滑模控制理论与模糊控制理论构成模糊滑模集成控制器，实现模糊控制与滑模控制的优势互补，能够保证系统的稳定并能抑制抖振，利用模糊技术还能有效地减弱传统滑模对不确定项的边界限制条件。

1　“四分之一”车悬架模型

图1为四分之一半主动悬架的结构简体模型。图中，ms为簧载质量；mr为非簧载质量；cs为悬架子系统阻尼系数；ks为悬架子系统刚度系数；kr为轮胎刚度系数；xi为路面激励位移；xs为簧载质量位移；xr为非簧载质量位移。

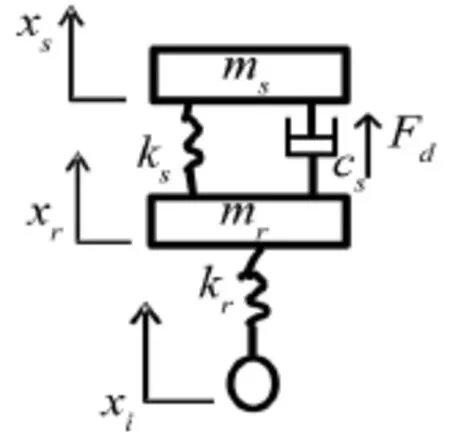
图1　四分之一半主动悬架的结构简体模型

采用牛顿第二定律建立其动力学方程为

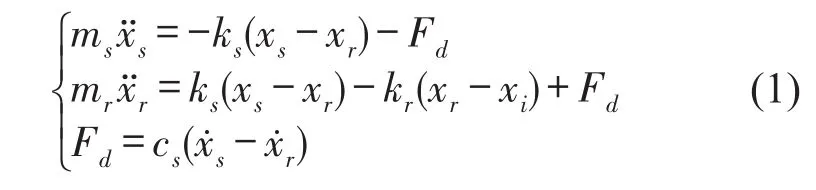
2　半车悬架动力学模型

通常情况下，汽车悬架系统的单轮模型为自由度模型，仅可以研究车体的垂直振动模式，不能研究其俯仰运动和侧倾运动，而半车模型悬架系统则可以研究其俯仰运动模式或是侧倾运动模式，本节主要研究半车模型被动悬架系统的纵向模型，即其俯仰运动模式，并研究车体俯仰运动形式和车体垂直运动形式［10］，本文建立半车半主动悬架的结构简体模型如图2所示。

图2　半车半主动悬架的结构简体模型

式中mg：车身簧载质量；mdr：前非簧载质量；mdf：后非簧载质量；Jθ：车身俯仰转动惯量；a、b：车身质心至后、前轴的轴距；csr：前悬架被动阻尼系数；csf：后悬架被动阻尼系数；ksr：前悬架子系统刚度；kmr：后悬架子系统刚度；kmr：前轮轮胎刚度系数；kmf：后轮轮胎刚度系数；xg，θ分别表示车辆质心垂直运动位移、车身俯仰运动的俯仰角；xsr（xsr=xg+bθ），xsf（xsf=xg-aθ），xur，xuf，xdr，xdf分别表示前后两个悬架子系统的簧载位移、非簧载位移以及前后两个轮胎簧载所承受的路面激励信号。

将（2）式两边乘以b与式（3）相减得

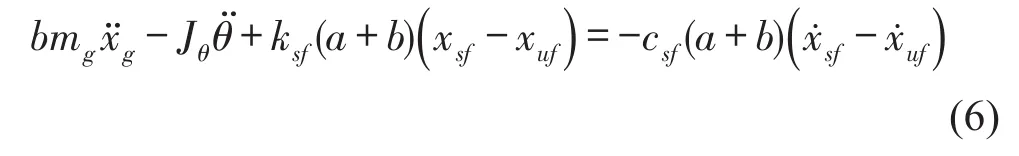
两边乘以a与式（3）相加得

由于俯仰角的量一般较小，因此前、后悬架子系统弹簧载位移可近似表示为

将式（8）和式（9）分别代入式（6）和式（7）整理得

结合式（12）和式（13），将式（10）和式（11）简化得

显然，式（16）和式（17）表示的半车前、后两组“四分之一”车辆悬架子系统，由于等效地补偿了式（14）和式（15）中的耦合阻尼力内和的影响，均与式（1）所示“四分之一”车辆悬架子系统的标准形式相同［12］。

为了实现半车前、后悬架子系统完全结构解耦就要解决如何实现和针对这个问题，可以采用反馈控制的方法，实时反馈车身俯仰角加速度变量，控制两组“四分之一”车辆悬架子系统的非簧载阻尼器，以产生所需的阻尼力。该半车前、后两组“四分之一”车辆悬架子系统的解耦控制器设计为

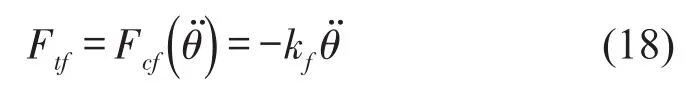
本文通过实时反馈车身俯仰角加速度变量，分别控制前、后非簧载阻尼器，使其产生用以补偿和的输出阻尼力，以实现半车系统俯仰运动姿态的平稳控制，达到半车前后悬架子系统完全结构解耦的目的；同时，本文应用己有“四分之一”悬架子系统分析“四分之一”座椅悬架并应用模糊滑模对其进行控制分析，通过独立控制前、后簧载可控阻尼器，实现半车悬架系统的垂直振动改善。

3　“四分之一”座椅悬架模型

图3为四分之一半主动悬架的结构简体模型。图中ms、mv、mt分别为座椅悬架（包括人体）、车身和轮胎的质量，zs、zv、zt分别为其对应的位移，ks、kv、kt和cs、cv分别为对应的系统的刚度系数和阻尼系数，Fd为减振器的可变阻尼力，z0为外界路面对系统的位移激励。

图3　四分之一半主动座椅悬架的结构简体模型

根据牛二定律建立相应的动力学方程为

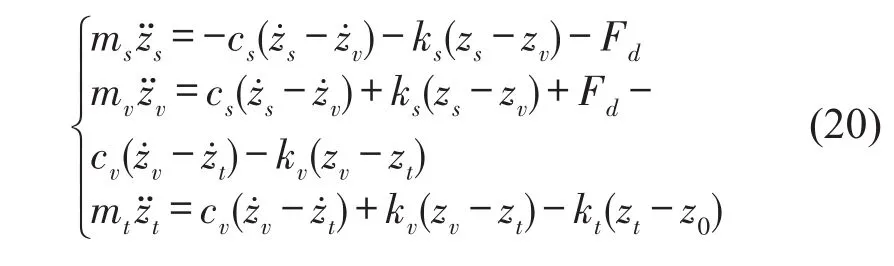
4　模糊滑模控制器

4.1滑模控制器的参考模型

采用带有天棚阻尼器的近似天棚阻尼系统（半主动）作为参考模型见图4。

此参考模型的动力学方程为

图4　参考模型

4.2滑模控制器的误差动力学模型

设计的滑模控制器是使实际被控系统的座椅悬架跟踪参考模型的运动，在两者的误差动力学系统中产生滑动模态。根据上述动力学模型，定义座椅悬架位移误差的积分、座椅悬架位移误差及速度误差为广义状态跟踪误差矢量

4.3滑模控制器的切换面设计

研究对象座椅悬架属于单输入系统（阻尼器产生的可变阻尼力），其切换面可表示为

通常cn=1，本文取n=3。将状态方程式（23）简化为

式（25）为滑动模态的运动微分方程。它决定了滑动模态的动态品质。式（25）的特征多项式为D（λ）=λ2+c2λ+c1，由于n=3，系统三个极点，故取其中一对共轭极点s1，s2为主导极点，另一个实极点s3为远极点。考虑到系统在滑动模态下的动态特性是渐近稳定的，故将滑模运动方程的特征根分布在复平面的左半平面上，特设定系统综合指标：σ≤15% ，tp≤0.7，故取阻尼系数 ζ=0.52，ωn=5.255，确定主导极点为-2.732 6±4.488 6 i，远极点为-20。切换函数的系数向量

系统进入滑模区域内的等效控制为u*，相应的系统滑模控制律为

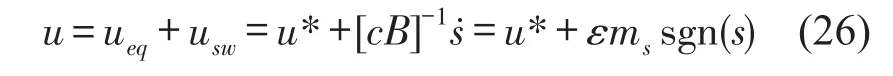
滑模控制下的实时可变阻尼力为

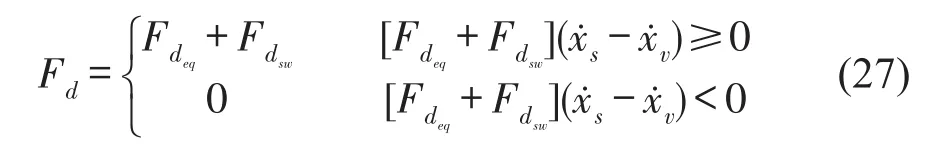
4.4模糊滑模控制器

为了使系统更加稳定，在前面滑模控制器的基础上加入模糊控制算法［13］。将s和̇作为二维模糊控制器的输入，分别表示系统距离滑模面的距离及其向滑模面趋近的速度，用模糊控制器的输出值的绝对值代替滑模控制器中的ε值，调整系统的稳定性。本文建立了基于滑模条件sṡ＜0的模糊规则，如表1所示。模糊滑模控制器的控制量为

式中εfuzzy为模糊滑模控制器的输出量。

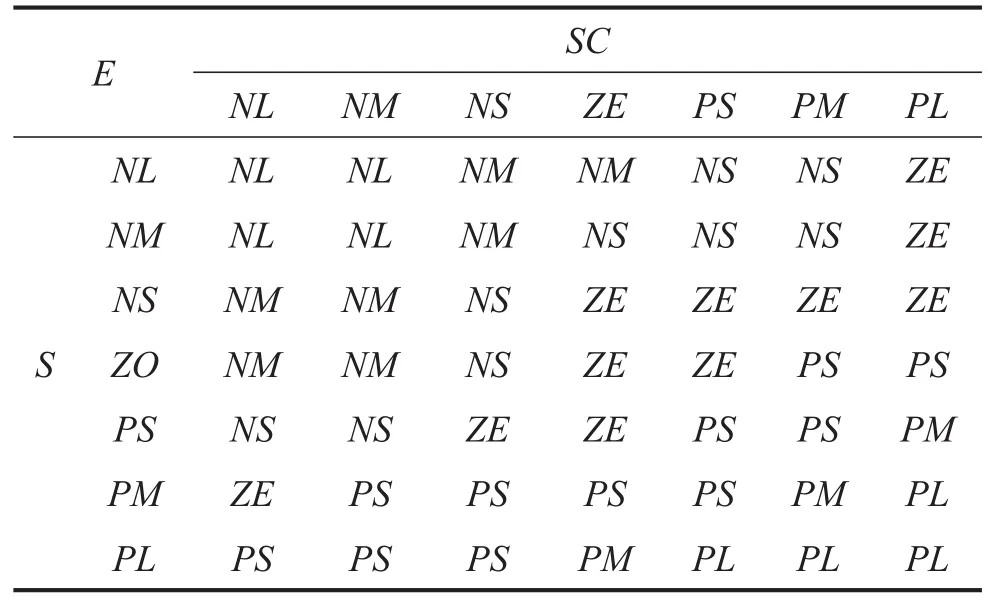
表1　模糊滑模规则

5　磁流变阻尼器控制策略

目前，调节减振器阻尼系数是半主动座椅悬架研究的关键技术之一。磁流变阻尼器的阻尼力可以通过外加磁场的变化而发生连续变化，且具有响应迅速，易实现计算机控制，减振降噪能力强，能耗低等优点，是半主动座椅悬架极具发展潜力的一类智能减振器。这里采用磁流变减振器对半主动座椅悬架进行控制，用Spencer等提出的修正的Bouc-Wen模型描述MR阻尼器的力学特性［11］。

利用如下公式获得跟踪期望控制力的磁流变阻尼器的电压

由式（29）得到提供给磁流变阻尼器的电压，如果阻尼器产生的力小于模糊滑模计算得到的力，提供给阻尼器的电压增加到最大水平，以增加阻尼器产生的力来匹配所需的控制力。否则，电压设置为零。

6　仿真分析

为验证所提出的模糊滑模控制器的优化效果，运用Matlab/Simulink进行仿真研究。如图5所示基于模糊滑模控制器的结构，且为有效的评价模糊滑模应用在半车半主动座椅悬架结构的效果。本文仿真的车辆数据参照文献［9］。

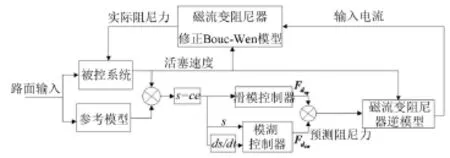
图5　模糊滑模控制器结构

图6为座椅悬架加速度的仿真结果，图7为座椅悬架动挠度的仿真结果。由图可知，基于半车悬架系统相比于被动悬架性能有明显的改善，表2为其相应的均方根值。由表2可知基于模糊滑模控制（fuzzy sliding mode controller（FSMC））的半车半主动悬架加速度较滑模（Sliding mode controller（SMC））、PID和被动悬架分别下降19.15%，27.19%，34.29%，动挠度分别下降了1.45%，2.81%和31.3%。随机路面激励下的座椅悬架加速度功率谱密度见图8。

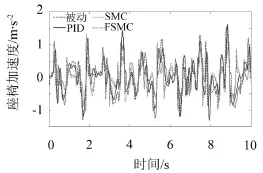
图6　座椅悬架加速度结果

图7　座椅悬架动挠度结果

图8　座椅悬架加速度功率谱密度

表2　不同悬架系统性能指标均方根值的对比分析

由图可以看出，相比于滑模、PID和被动作用下的座椅加速度在大部分频率段内明显地降低，改善了车辆运行的平顺性。在车身共振（1 Hz～1.5 Hz）和椅面垂直最敏感（4 Hz～12.5 Hz）的低频范围内，模糊滑模较其他方法有效地降低了座椅的加速度，在4 Hz～8 Hz这个人体内脏器官易产生共振的频率范围内，模糊滑模控制较其他控制加速度均有明显降低，进而减轻乘客的不适应性。由此可见此方法有效降低了车身振动对人体的影响，显著提高了车辆悬架系统的动态舒适性。

7　结语

本文首先搭建了半车车辆座椅悬架的测试系统，并把半车悬架系统解耦成四分之一车悬架系统。将模糊和滑模控制的优点相结合，以四分之一车半主动座椅悬架和被动悬架做了对比试验，在半主动控制中，运用了模糊滑模（FSM）、滑模（SM）和PID不同的控制方法，给出了不同测试条件下的控制结果，并对数据和图表展开了分析和评价。试验结果表明：本文提出的半车磁流变阻尼器模型的模糊滑模变结构控制比滑模、PID控制及被动系统下的座椅悬架加速度分别下降了19.15%，27.19%，34.29%，证实了此模糊滑模变结构控制器的有效性。

［1］MARGOLIS D L.Procedure for comparing passive，active and semi-active approaches to vibration isolation［J］. Journal of the Franklin Institute，1983，315（4）:225-238.

［2］吴龙，闻霞.6自由度半车悬架解耦及其分层振动控制的研究［J］.汽车工程，2010，32（2）：148-155.

［3］NGUYEN S D，NGUYEN Q H，CHOI S B.A hybrid clustering based fuzzy structure for vibration control-Part 2:An application to semi-active vehicle seatsuspension［J］.MechanicalSystemsandSignal Processing，2015，56-57（5）:288-301.

［4］PRABAKA RS，SUJATHA C，NARAYANANS. Optimal semi-active preview control response of a half car vehiclemodelwith magnetorheological damper［J］.Journal of Sound and Vibration，2009，326（3-5）:400-420.

［5］SUNG KUM-QIL，HAN YOUNG-MIN，CHO JAE-WAN，et al.Vibration control of vehicle ER suspension system using fuzzy moving sliding mode controller［J］.Journal of Sound and Vibration，2008，311:1004-1019.

［6］朱华.半主动悬架车辆平顺性建模与联合仿真研究［D］.浙江：浙江大学，2010.

［7］吴参.车辆半主动悬架非线性特性与控制算法研究［D］.杭州：浙江大学，2010.

［8］董小闵，余淼，陈伟明，等.汽车磁流变半主动悬架分姿态协调仿人智能控制方法［J］.中国机械工程，2007，18（7）：764-769.

［9］陈云微，赵强.车辆半主动座椅悬架滑模变结构控制［J］.哈尔滨工程大学学报，2012，33（6）：775-778.

［10］张海龙.半车悬架系统的结构解耦控制研究［D］.南京：南京师范大学，2013.

［11］赵强，米磊，尹佳星.基于磁流变阻尼器的车辆悬架振动优化控制［J］.武汉理工大学学报（交通科学与工程版）2013，37（2）：241-245.

［12］黄苗玉.磁流变智能车辆悬架的混沌分析与控制［D］.南京：南京师范大学，2015.

［13］靳宝全.电液位置伺服控制系统的模糊滑模控制方法研究［D］.太原：太原理工大学，2010.

Fuzzy Sliding Mode Control of Semi-active Suspension Based on Half-car Decoupling

ZHAOQiang，ZHANGNa
（Traffic College，Northeast Forestry University，Harbin 150040，China）

To improve car comfort，a fuzzy sliding mode control for semi-active seat suspension based on half-car decoupling model is proposed.First of all，the half-car dynamic model of the passive suspension system is established and analyzed.Then，it is converted equivalently into two sets of typical dynamic equations.Therefore，decoupling of the half-car suspension system into a quarter-car suspension system is realized.A fuzzy sliding mode controller（FSMC）for the semiactive seat suspension based on the decoupled quarter car is proposed.In the FSMC，an ideal skyhook model is taken as the reference model，and the dynamic errors between the seat suspension and reference model are introduced to the sliding mode.Further the fuzzy strategy is used suppress the chattering occurred in the above sliding mode control by fuzzifying the switch function and its derivative.by comparing the output force of the magnetorheological（MR）damper with the desired force solved by the fuzzy sliding mode controller，the voltage to control the MR damper is calculated.The comparison results of FSMC with PID，sliding mode control by numerical simulations show that the vibration reduction effect of the semi-active seat is obviously improved.The proposed method provides a reference for the control of the semi-active seats.

vibration and wave；semi-active suspension；half of decoupling；MR damper；fuzzy sliding mode controller

TB53

ADOI编码：10.3969/j.issn.1006-1335.2016.05.013

1006-1355（2016）05-0059-06

2016-05-27

黑龙江省自然科学基金项目资助（LC2015019）

赵强（1971-），男，黑龙江省富锦人，博士，博士生导师，主要研究方向为车辆动力学与控制。

张娜，女，博士生。E-mail:zn654715834@qq.com