受路面随机激励作用车室低频耦合轰鸣声分析
2016-11-09李苏平胡启国胡海波罗天洪
李苏平,胡启国,胡海波,罗天洪
(1.重庆交通大学 交通运输学院,重庆 400074;2.重庆交通大学 机电与车辆工程学院,重庆 400074)
受路面随机激励作用车室低频耦合轰鸣声分析
李苏平1,胡启国2,胡海波2,罗天洪2
(1.重庆交通大学 交通运输学院,重庆 400074;2.重庆交通大学 机电与车辆工程学院,重庆 400074)
为分析车室受路面随机激励作用产生的低频轰鸣声,采用白噪声过滤方法模拟路面随机激励,建立路面随机激励时域模型,根据拉格朗日原理建立整车七自由度振动动力学模型,利用Matlab建立受路面随机激励作用引起的悬架激励力仿真模型,并通过快速傅里叶变换得到悬架激励力幅频谱。利用Hypermesh建立车身结构有限元模型和空腔声场有限元模型,分别利用Nastran、Virtual.Lab计算车身结构模态和空腔声场模态,并采用模态叠加法计算声固耦合系统模态,最后施加悬架激励力载荷进行基于模态的耦合声学响应分析。分析结果表明:在频率20 Hz~50 Hz范围内,路面随机激励对车室低频耦合轰鸣声的贡献较大,以结构变形为主的耦合系统模态,受路面随机激励作用极易使车室空腔出现低频耦合轰鸣声。
声学;声固耦合;低频轰鸣声;路面随机激励;车室
车室空气处于密闭状态时,会有许多振动模态或声腔模态,若密闭空腔受到压缩,其体积会发生变化并产生很高的阻抗,空腔周围的车身板件会与声场发生耦合作用。车室的这种耦合作用在外界激励力的作用下,如果响应过高会产生较大的声压脉动,形成轰鸣声[1],这种在窄频带内能量分布较高的噪声,不仅降低车辆的声学舒适性,而且容易引起乘客的胸闷、恶心、头晕等不适症状。
车室轰鸣声属于低频噪声。根据激励源的不同可分为发动机怠速轰鸣声、路面激励轰鸣声、传动系统激励轰鸣声、排气系统轰鸣声等[2]。其中路面激励轰鸣声主要频率在20 Hz~100 Hz范围内。国内外学者对车室声固耦合机理及低频噪声进行了许多研究[3-6],而少有从路面随机激励作用角度研究车室低频轰鸣声的。为分析车室声固耦合系统因受路面随机激励作用,产生的频率在20 Hz~100 Hz的轰鸣声,建立车室声固耦合模型,利用白噪声过滤方法模拟路面随机激励,分析路面激励轰鸣声的产生机理,对车室轰鸣声的控制研究具有指导作用。
1 路面随机激励
车辆所受的路面随机激励作用,实际上是由路面随机不平引起的悬架作用于车身的激励力。因路面激励具有随机特性,故悬架激励力也具有随机特性。为计算悬架对车身的激励力,采用白噪声过滤方法模拟路面随机不平度激励,建立路面随机激励时域模型和整车七自由度振动动力学模型,利用Matlab/Simulink建立悬架激励力仿真模型,计算悬架对车身的激励力,再经快速傅里叶变换得到悬架激励力幅频特性曲线。
1.1路面随机激励时域模型
车轮与路面接触处的单点激励满足[7]
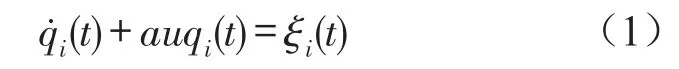
其中qi(t):i点激励高程时间样本;u:车速;a:与路面等级相关的路面常数;ξi(t):均值为零的白噪声随机信号。
同侧前后轮所受激励存在迟滞性,单轮辙激励模型为
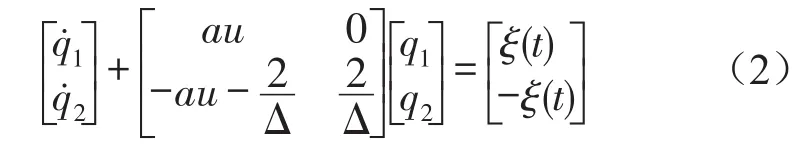
左右两侧车轮轮迹具有异辙空间相关性,设左侧(x)轮辙白噪声输入为ξx,右侧(y)轮撤白噪声输入为ξy。左右两侧轮辙的相关性方程为
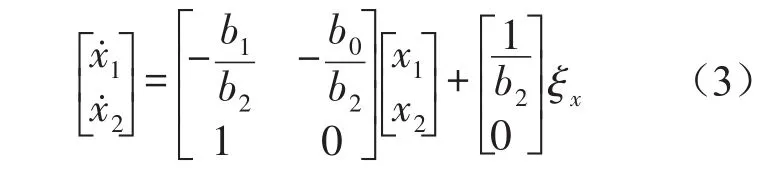
则右侧轮撤白噪声输入模型为
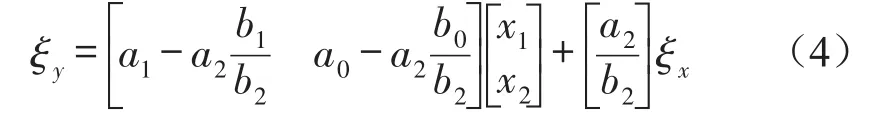
其中a0、a1、a2、b0、b1、b2为道路品质常数;x1、x2为中间状态变量。由以上各式即构成车辆所受路面随机激励时域模型。
因C级路面路况相对A、B级路面较差,对车室声学环境的影响较大,故假定车辆在C级道路上行驶,仿真得到车速为50 km/h时,汽车四轮所受路面随机激励如图1所示。
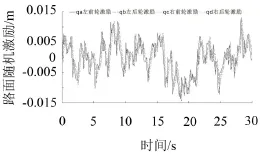
图1 汽车四轮所受C级路面随机激励
车辆四轮所受路面随机不平度激励qi满足条件|qi|<0.02 m,并且与文献[8]中C级路面实测结果基本吻合,故通过白噪声过滤方法模拟路面随机激励是可行的。
1.2整车振动动力学模型
整车七自由度振动动力学模型如图2所示。七个自由度包括四个车轮的垂直振动自由度,车身的垂直、俯仰和侧倾三个自由度。
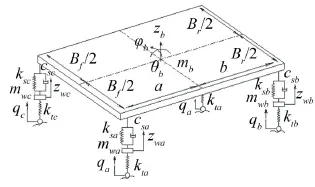
图2 整车七自由度振动动力学模型
图中mwa、mwb、mwc、mwd——车轮质量;mb——簧载质量;kta、ktb、ktc、ktd——轮胎刚度系数;ksa、ksb、ksc、ksd——悬架刚度系数;csa、csb、csc、csd——悬架阻尼系数;qa、qb、qc、qd——车轮受到的路面随机不平度激励;zwa、zwb、zwc、zwd——轮胎质心处垂直位移;zb——车身垂直位移;θb——车身俯仰角;φb——车身侧倾角;Bf、Br——车前后轮轮距;a——车前轴至车体质心的距离;b——车后轴至车体质心的距离。
振动系统微分方程可以根据第二类拉格朗日方程推导
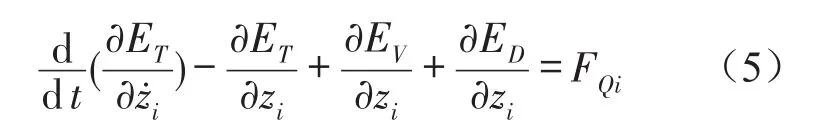
其中ET:系统总动能;Eν:系统总势能;ED:系统总耗散能;zi:第i个质点的广义坐标;FQi:对应于坐标zi的广义主动力。
系统广义坐标为
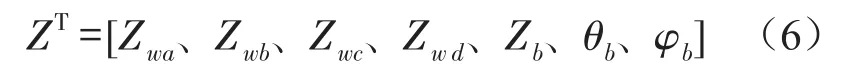
系统总动能

将式(7)、式(8)、式(9)代入到式(5)中得到振动系统的运动微分方程
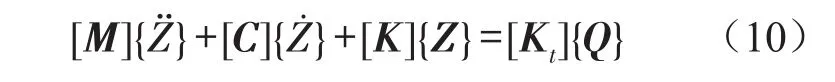
其中{Z} :7×1的位移矩阵;[M]:7×7的系统质量矩阵;[C]:7×7的系统阻尼矩阵;[K]:7×7的系统刚度矩阵;[Kt]:7×4的轮胎刚度矩阵;{Q}:4×1的路面随机不平度激励矩阵。
1.3悬架作用于车身的激励力
以左前车轮(a轮)为例,求悬架对车身的作用力。受力分析如图3所示。
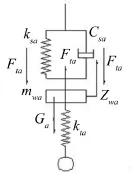
图3 受力分析
对左前车轮,根据牛顿第二定律
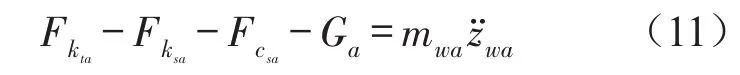
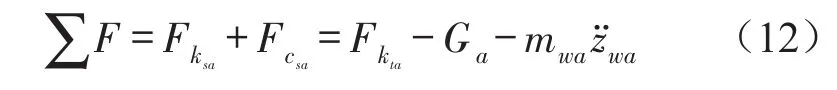
式(12)中各力的计算式为
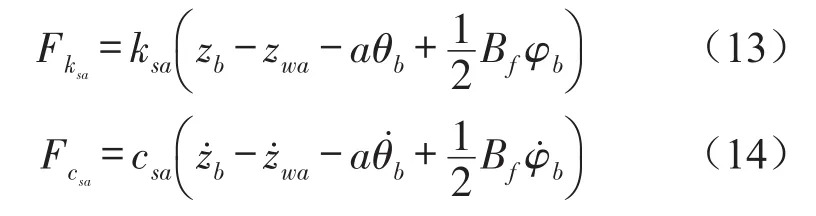
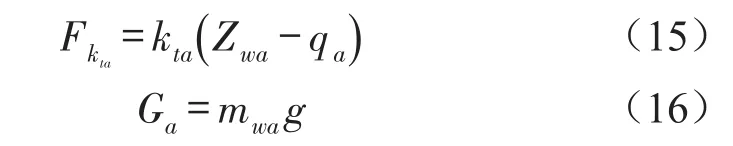
根据二力平衡原理和牛顿第三定律,悬架作用于车身的激励力Fa为
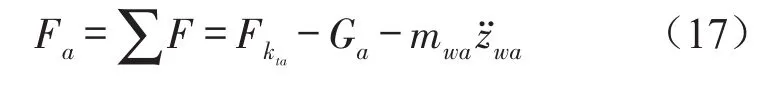
1.4悬架激励力Simulink模型
根据建立的路面随机激励时域模型、整车七自由度振动动力学模型和悬架激励力计算式,利用Matlab/Simulink建立仿真模型,求悬架作用于车身的激励力。悬架激励力仿真模型如图4所示。
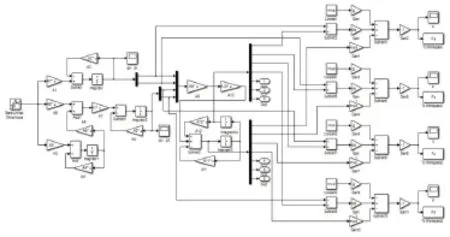
图4 悬架激励力Simulink模型
1.5悬架激励力幅频谱
因悬架作用于车身的激励力大小与车速有关,故为分析车辆在C级路面以不同车速行驶时,受路面随机激励作用车室产生的低频轰鸣声,分别计算了车速为30 km/h、50 km/h、80 km/h、120 km/h时的悬架激励力,并通过快速傅里叶变换将时域内的悬架激励力转换到频域,得到不同车速下的悬架激励力幅频谱,如图5所示。
由悬架激励力幅频特性知,不同车速下的悬架激励力幅频特性曲线变化趋势基本一致,且悬架激励力均主要集中在50 Hz以内的低频范围内,频率大于50 Hz的激励力均较小且波动幅度不大,这满足由路面随机不平引起的激振力主要集中在较低频范围内的特点,所以计算得到的悬架激励力是合理的。频率低于20 Hz的激励力幅值虽然较大,但由于人耳所能听到的声音频率下限为20 Hz,且车身第1阶模态频率一般均要高于20 Hz,所以在分析车室耦合响应噪声时,主要考虑频率分布在20 Hz~50 Hz的悬架激励力,并且根据激励力幅频谱,在该频率范围内,随车速的提高,悬架激励力幅值也在逐渐增大。
2 结构与声场有限元模型
2.1.车身结构有限元模型
由于车身结构复杂,建立有限模型时,在不影响其主要特性的前提下进行了适当简化。因为车身结构主要由薄壁板件组成,所以建模时利用壳单元进行离散化。利用Hypermesh进行前处理,综合考虑计算精度和工作量,取网格单元尺寸为10 mm,建立的车身结构有限元模型如图6所示,共含有444 150个单元,464 592个节点。
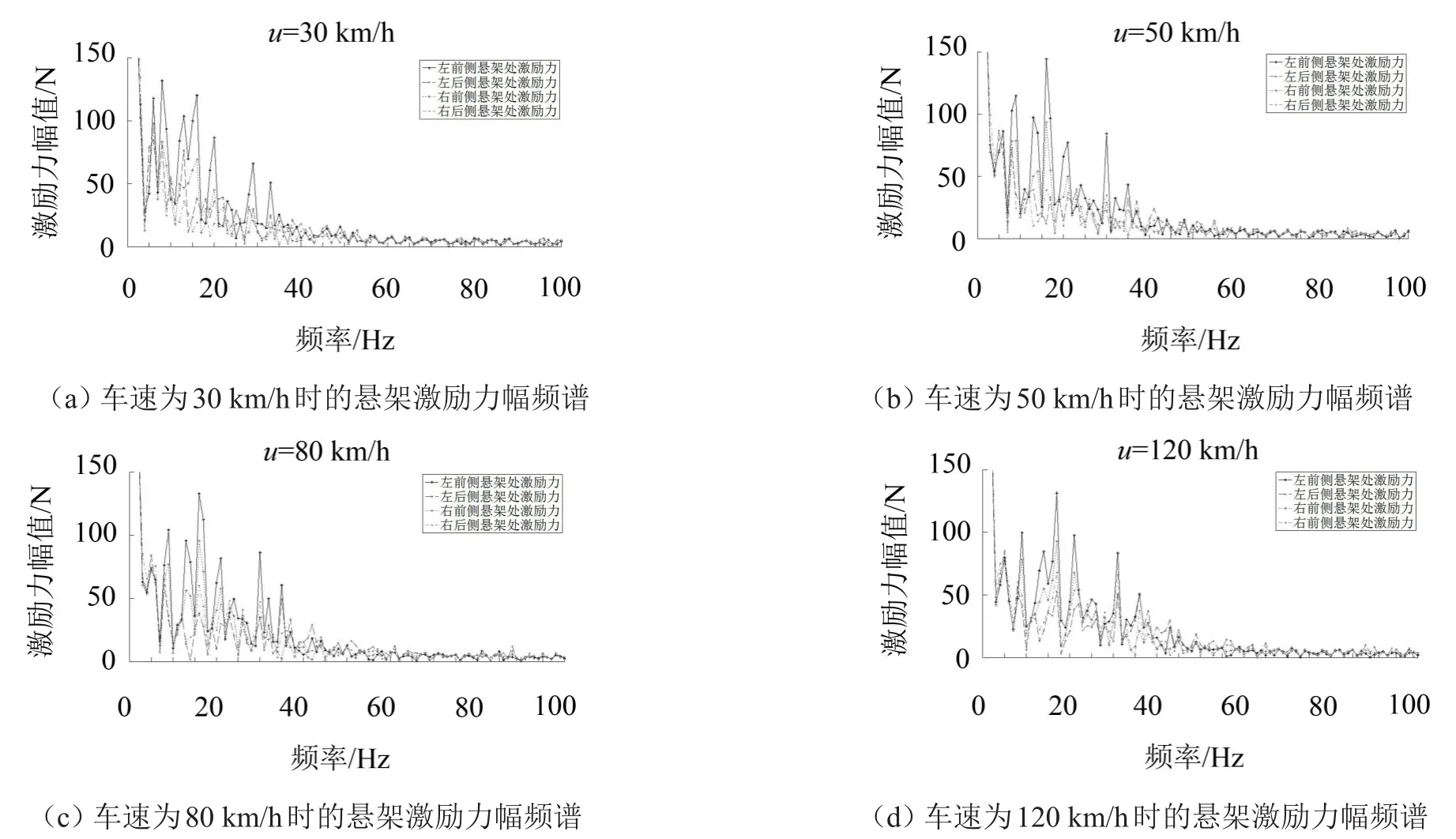
图5 不同车速下悬架激励力幅频谱

图6 车身结构有限元模型
2.2空腔声场有限元模型
对车身板件围成的车室密闭空腔,利用四面体单元进行网格划分。因座椅对空腔声场分布影响较大[9~10],故在建立声腔有限元模型时,也建立了座椅模型。在Hypermesh中建立的空腔声场有限元模型如图7所示,其中共有29 467个网格单元,6 229个节点。

图7 车室空腔声场有限元模型
3 模态分析
3.1车身结构模态分析
在Nastran中利用Lanczos方法对车身结构进行模态计算。因未施加载荷和约束,进行的是自由模态计算,故计算结果前6阶为刚体模态。由于车身结构以薄壁板件为主,整车模态频率分布较密且存在较多局部模态。车身结构第7~16阶模态如表1所示。

表1 车身结构模态分布
3.2空腔声场模态分析
在Virtual.Lab中利用Lanczos方法计算空腔声场声学模态,在频率0~150 Hz范围内的声学模态如表2所示。

表2 空腔声场声学模态分布
3.3结构-声场耦合系统模态分析
通过定义网格映射关系建立结构-声场耦合模型,设定网格间映射算法为在声学网格某一节点半径为150 mm的圆域内,最多有4个结构网格上的节点作为该声学网格节点的原始数据。利用结构模态和声场模态计算结果,在Virtual.Lab中利用模态叠加法计算声固耦合系统在频率0~100 Hz范围内的耦合模态。耦合系统第4~23阶耦合模态分析结果见下表3所示。
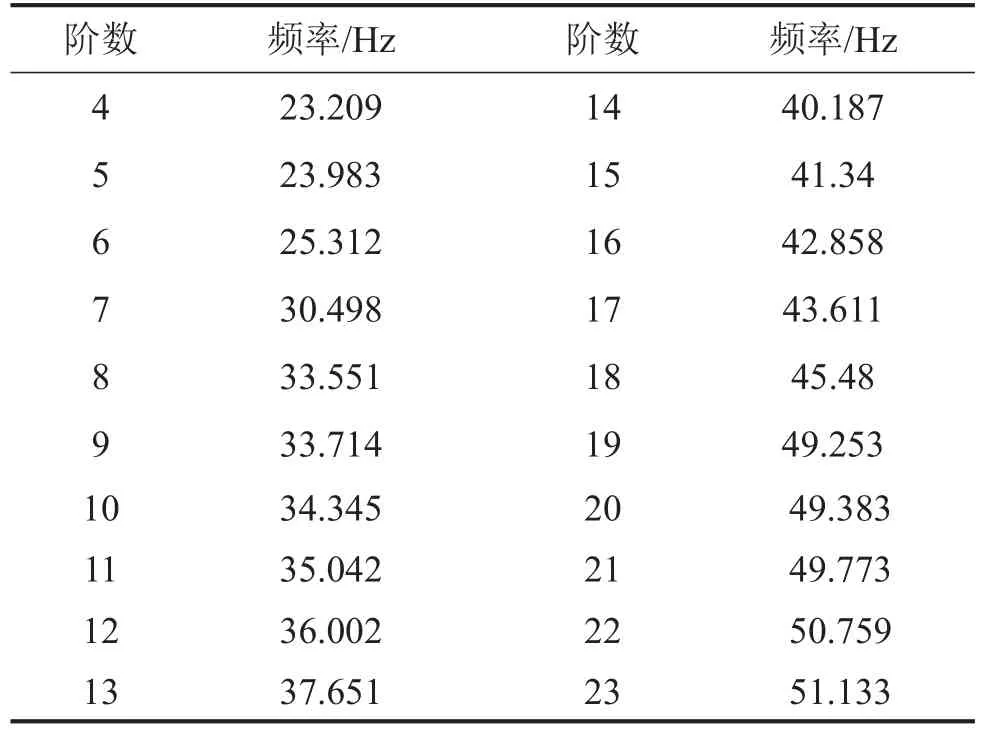
表3 声固耦合模态分布
声固耦合模态与车身结构模态相比,模态分布非常相似,模态频率稍有变化,但频率改变均未超过1 Hz。由于耦合系统模态是由车身结构与空腔声场相互作用形成的,而在0~100 Hz范围内空腔声场仅存在第2阶模态(59.622 Hz),耦合系统模态分布规律又与结构模态分布非常相似,所以在该频率范围内耦合系统模态主要是以结构变形为主的耦合模态,在空腔声场第2阶模态附近才会出现以空腔声压变化为主的耦合模态。故车室声固耦合系统在0~100 Hz频率范围内受到外界激励力作用时,在耦合频率附近易使车室产生低频噪声。
4 车室低频耦合轰鸣声分析
分别加载不同车速下的悬架激励力,在Virtual. Lab中对车室声固耦合系统进行基于模态的声振耦合响应分析,计算频率范围为20 Hz~100 Hz,计算步长取1 Hz。在驾驶员头部处定义一场点,作为声压响应输出点。则车辆在C级路面以不同车速行驶时,车室空腔测点的A计权声压曲线如图8所示。
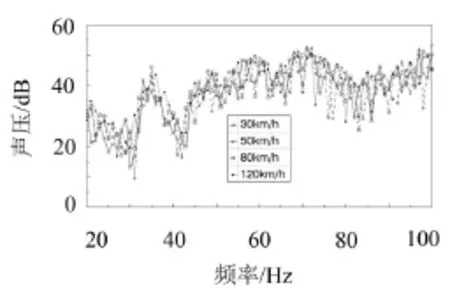
图8 不同车速下测点的A计权声压曲线
根据测点的A计权声压曲线,不同车速下的测点声压变化趋势基本一致,测点声压幅值在声压较低的频率附近均较低,在声压较高的频率附近均较高。说明以不同的车速通过同一路面时,车室声固耦合系统的声学特性主要由耦合系统自身的固有特性和路面随机激励特性决定,不同车速下的悬架激励力主要影响测点的声压幅值,而不会改变测点声压的变化趋势。随车速的提高,各频率处的测点声压幅值总体呈逐渐增大的趋势。故在路况较差的道路上行驶时,可以通过降低行驶车速的方法来减小车内噪声。
在频率20 Hz~50 Hz的范围内,测点声压曲线变化幅度很大,声压峰值发生了连续较大的波动。特别是在频率35 Hz附近,测点声压峰值达到了45 dB,而在频率31 Hz和42 Hz附近测点声压峰值又较低,最低声压值分别约为7 dB和15 dB,这与频率35 Hz处的声压峰值分别相差约38 dB和30 dB,使得在频率31 Hz~42 Hz的范围内,测点声压峰值在较窄频带内连续两次发生较大波动,从而使车室出现低频轰鸣声。由表3知耦合系统在35 Hz附近存在较多模态分布,且悬架激励力幅值在35 Hz处也较大,所以耦合系统受激振力作用发生共振产生较大声压峰值。而在频率31 Hz和42 Hz处耦合系统无模态分布,且悬架激励力也较小,所以测点声压较低。故在频率20 Hz~50 Hz的范围内,由路面随机激励引起的悬架激励力对车室低频耦合轰鸣声的贡献较大。
在频率50 Hz~100 Hz范围内,图5中不同车速下的悬架激励力均稳定在较小水平,图8所示的测点声压曲线变化幅度较小,在窄频带内也未出现连续较大的声压波动,故在该频率范围内由路面随机激励引起的悬架激励力对车室低频轰鸣声的贡献较小。
综上所述,在频率20 Hz~50 Hz范围内,以结构变形为主的耦合系统模态受路面随机激励作用极易使车室出现轰鸣声,若长时间受这种低频轰鸣声的刺激,会使乘员出现生理和心理上的极度不适。因为这种低频轰鸣声主要由以结构变形为主的耦合模态受激励力作用而出现,所以可以通过优化车身结构以改变耦合系统模态的方式来控制。
5 结语
(1)采用白噪声过滤方法来模拟路面随机激励是可行的。通过建立路面随机激励时域模型和整车七自由度振动动力学模型,利用Matlab建立仿真模型,经仿真计算得到的悬架作用于车身的激励力是合理的。使车室空腔出现轰鸣声的悬架激励力频率,主要集中在20 Hz~50 Hz的范围内。
(2)在频率0~100 Hz范围内,车室声固耦合系统模态主要是以结构变形为主的耦合模态。在该频率范围内,耦合系统受到外界激励力作用时,易使车室在耦合频率附近产生低频噪声。
(3)受路面随机激励引起的悬架激励力作用,在频率20 Hz~50 Hz的范围内,测点声压峰值在窄频带内发生了连续较大的声压波动,路面随机激励对车室低频耦合轰鸣声的贡献较大;而在50 Hz~100 Hz范围内,路面随机激励对车室低频耦合轰鸣声的贡献较小。故在20 Hz~50 Hz的频率范围内,以车身结构变形为主的声固耦合模态,受路面随机激励作用极易使车室空腔出现低频耦合轰鸣声。
[1]王志亮,刘波,王磊.轿车轰鸣声产生机理与分析方法研究[J].噪声与振动控制,2008,28(2):79-81.
[2]庞剑,谌刚,何华.汽车噪声与振动[M].北京:北京理工大学,2006.
[3]LAURENT G,MORAD K,ENERGY D.Filed approach for low and medium-frequency vibration acoustic analysis of a car body using a probabilistic computational model[R].SAE,2009.
[4]马天飞,林逸,张建伟.轿车车室声固耦合系统的模态分析[J].机械工程学报,2005(7):225-230.
[5]朱才朝,秦大同,李润方.车身结构振动与车内噪声声场耦合分析与控制[J].机械工程学报,2002(8):54-58.
[6]惠巍,刘更,吴立言.轿车声固耦合低频噪声的有限元分析[J].汽车工程,2006(12):1070-1073.
[7]张永林,钟毅芳.汽车道路双轮辙多点随机激励建模与仿真研究[J].系统仿真学报,2004(6):1147-1149+1154.
[8]檀润华,陈鹰.路面随机激励下的汽车振动仿真[J].振动、测试与诊断,2000,20(2):119-122.
[9]白胜勇,靳晓雄,丁玉兰,等.轿车乘坐室声学模态分析[J],同济大学学报,2000(2):206-209.
[10]刘禹,喻凡,柳江.车辆乘坐室声固耦合模态分析[J].噪声与振动控制,2005,25(5):38-40+67.
Analysis of Low Frequency Coupled Booming of Passenger Compartments Induced by Road Random Excitation
LI Su-ping1,HU Qi-guo2,HU Hai-bo2,LUO Tian-hong2
(1.College of Traffic and Transportation,Chongqing Jiaotong University,Chongqing 400074,China;2.School of Mechanotronics and Vehicle Engineering,Chongqing Jiaotong University,Chongqing 400074,China)
To analyze the low frequency booming of the passenger compartments under road random excitation,the time domain model for road random-excitation simulation is established using white noise filtering method.Based on Lagrange principle,a 7-DOF dynamic model for the whole vehicle is set up.The simulation model for suspension excitation force caused by the road random excitation is built by means of Matlab and the amplitude frequency spectrum of the suspension excitation force is obtained by FFT method.A structural FEM for vehicle body and an acoustic FEM for interior cavity are established using Hypermesh.Structure modal analysis and cavity acoustic modal analysis are computed by using Nastran and Virtual.Lab.Then,the structure-acoustic coupling system modals are computed through modal superposition method.Finally,the coupled acoustic response analysis based on the modals is performed by applying the suspension excitation force load.The analysis results indicate that in the frequency range of 20 Hz-50 Hz,the road random excitation has a large contribution to the low frequency booming of the passenger compartments.The coupled system modals dominated by structure deformation can readily lead to low-frequency booming in the passenger compartments under the road random excitation.
acoustics;structure-acoustic coupling;low frequency booming;road random excitation;passenger compartment
TB533+.2
ADOI编码:10.3969/j.issn.1006-1335.2016.05.011
1006-1355(2016)05-0050-06
2016-04-10
重庆市基础科学与前沿技术研究专项重点资助项目(cstc2015jcyjBX0133);国家自然科学基金资助项目(51375519)
李苏平(1989-),男,湖北省公安县人,硕士研究生,主要研究方向为噪声振动控制。E-mail:ataizz@139.com
胡启国(1968-),男,硕士生导师。E-mail:swpihqg@126.com
