无线传感器网络中四元无线声阵列节点选择及目标定位算法

朱海洋,张合,马少杰,潘菡

(南京理工大学机械工程学院,江苏南京210094)

无线传感器网络中四元无线声阵列节点选择及目标定位算法

朱海洋,张合,马少杰,潘菡

(南京理工大学机械工程学院,江苏南京210094)

低成本、小型化的无线声传感器网络(WASN)的每个节点只配备一个麦克风而非麦克风阵列,针对随机抛撒的WASN区域外声源目标定位问题,依据声压衰减模型和几何定位机制,提出了四节点无线声阵列声源定位算法。在此基础上分析了声音衰减系数和阵列形状对定位精度的影响,进而选择以Y型阵列作为感知模型,当Y型阵列的中轴线与目标声源的夹角为60°～100°时,定位误差小于1 m.依据仿真结果提出节点选择算法并进行了Y型阵列目标定位实验,结果表明,Y型无线声传感器阵列满足对无线传感器网络(WSN)抛撒区域外50 m处目标的预警需求。

兵器科学与技术;无线声传感器网络;四元无线声传感器阵列;节点选择;目标定位

DOI:10.3969/j.issn.1000-1093.2016.01.013

0 引言

传声器阵列被广泛地应用于陆上与水下目标探测、识别与跟踪等军事领域。传统的声传感器阵列的各阵元通过有线方式连接,根据阵列形状的不同可分为线阵、四元平面方阵、五元十字阵、圆阵和四元立体方阵等。这种固定声阵列的节点体积较大,限制了阵列部署的灵活性。随着信号处理技术和通讯技术的进步,使得多个空间分布的声传感器节点通过无线通信媒介连接而成的无线声传感器网络(WASN)成为可能。

WASN中的每个传感器节点只配备一个麦克风作为感知设备,节点间通过无线通信方式连接,因此节点体积小,价格便宜,可通过更随意的方式大规模部署在监测区域。对于随机抛撒的WASN目标声源定位,由于没有事先存在的传感器阵列,因此首要问题是在节点数量较多的WASN中选择合适的节点组成阵列,节点选择算法能够使建立的目标定位算法得到更高的定位精度,令能源受限的无线传感器网络(WSN)得到最大生存时间。针对不同的目标定位算法,节点选择算法也会有所不同。目前,大量关于WASN的研究都集中于节点抛撒区域内部的声源定位与跟踪,大部分的算法都是利用如下3种物理量进行定位的:信号到达时间差(TDOA)、到达角度(DOA)和接收信号能量(RSS).TDOA方法[1-4]对于定位宽带信号目标具有良好的效果,而DOA算法对于定位窄带信号目标具有良好的效果。然而,TDOA方法和DOA方法[5]要求传感器节点之间有精确的时间同步,并且采样频率必须足够高才能截取信号有效特征,这些在WSN的应用中是较为困难的[6-7]。RSS目标定位算法对硬件要求低,计算量小,因此更加适应WSN的应用环境。对于多目标定位常用极大似然估计法[8-11],而对于单目标定位常用最近点法、质心法和最小二乘法。最小二乘法需要通过大量节点迭代[12-14],而最近点法和质心法只适用于定位抛撒区域内部的声源目标。

上述算法没有一种适用于WSN抛撒区域外目标定位情况。本文依据声压衰减模型和几何定位机制,提出基于能量的四节点声阵列目标定位算法,对处于WASN抛撒区域外的目标声源进行初步定位和预警。在对影响定位算法精度的误差源分析的基础上,进一步提出节点选择算法。

1 四元无线声传感器阵列目标定位算法

WASN中包含一个网关节点和数量较多的传感器节点,可通过飞机或火箭大规模部署在远距离监测区域,如图1所示。每个传感器节点一个麦克风作为感知设备,一个微处理器用于数据和信号处理,一个无线数据传输模块用于信息交换和一个电池作为电源供应。一定数量的信标节点同时配备一个定位模块获取自身位置,各节点通过射频组成无线多跳自组织网络。网关节点除了上述硬件,还配备北斗一代通信模块,从而通过北斗一代通讯卫星与远距离控制中心建立通讯链路。节点间可通过基于测距的节点自定位算法并辅以信标节点的物理位置,对各节点进行定位,本文假设各节点位置已知。

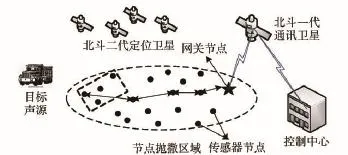
图1 WASN目标声源定位示意图Fig.1 Schematic diagram of source localization in WASN

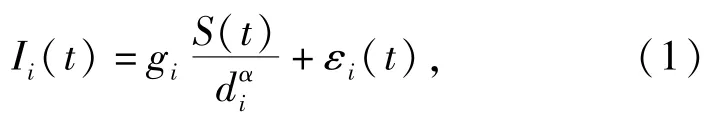
式中:Ii(t)为节点i在时间t的测量声音能量值; S(t)为距声源单位距离处得到的能量值;di为节点i与声源之间的距离;gi为节点i的校正因子,取值为1;α为声音衰减系数;εi(t)为模型误差和观测误差之和。在实际应用中,测量某一时刻的瞬时声压意义不大,往往在一个时间间隔内多次取值,并通过短时能量法求得这段时间内的能量值。根据声音衰减公式并结合几何定位法,提出基于能量法的四元分布式声阵列目标定位算法。对于节点i,(1)式整理后可得

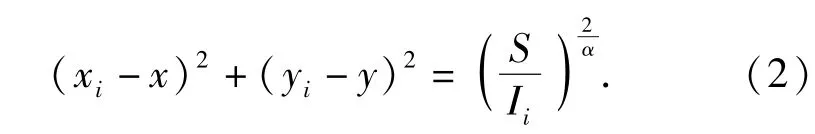
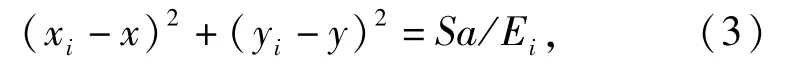
则节点j得到(4)式对应的方程

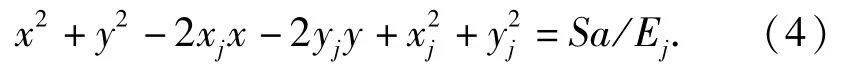
(3)式与(4)式相减可得

此算法最少需要3个独立的方程来求解未知数,因此至少需要4个节点参与目标的定位计算。对于四节点模型,可得方程组

式中:(χ,y)为目标位置;(χk,yk)为第k个传感器节点的位置。

(5)式可写成矩阵形式

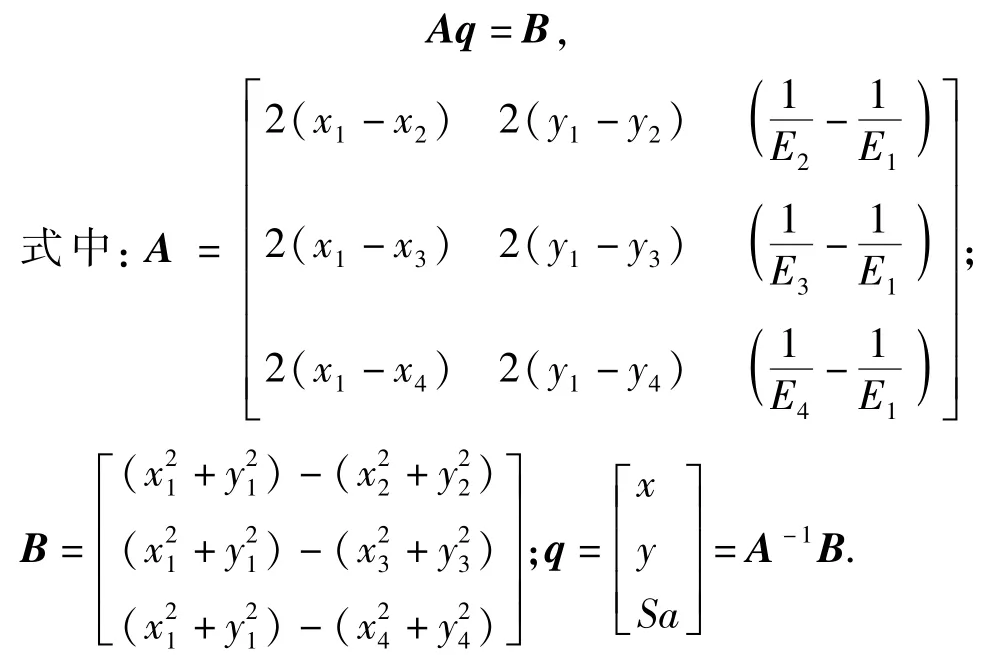
由于存在背景噪声,实际测得的声音能量并不准确,导致方程组在求解时产生定位误差 Δd=

2 目标定位算法误差源分析

定位误差的主要来源是背景噪声,会导致定位算法产生误差。而不恰当的声音衰减系数和不合理的四节点模型会导致定位误差变大甚至定位算法无解。因此在存在背景噪声的情况下,研究能够使定位误差在合理的范围内的最佳声音衰减系数和四节点模型显得尤为重要。由于节点是随机撒布的,因此很难从数学表达式上分析出形状、尺寸和方位角对误差的影响。因此本文采用控制变量法来研究,通过大量的仿真计算获取可使误差相对较小的声音衰减系数和最优四节点模型。

2.1 声音衰减系数

实际的测量环境中,声音衰减系数 α≠2,若(1)式仍然按照α=2进行求解,会产生较大定位误差。为了量化声音衰减系数对定位精度的影响大小,本文对不同声音衰减系数下的定位误差进行仿真分析。设β=α/2,其中α为实际声音衰减系数,理论声音衰减系数为2,在不同的实际声音衰减的环境中,(1)式利用实际声音衰减系数与利用理论声音衰减系数的定位误差仿真结果如图2所示。

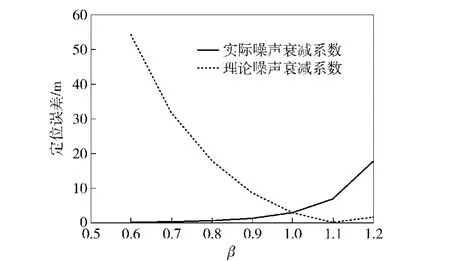
图2 噪声衰减系数对定位精度的影响Fig.2 Influence of attenuation coefficient on positional accuracy

由图2可知:当β＜1.0时,(1)式利用理论噪声衰减系数α=2求解的误差值比按实际环境下的α值所得的定位误差值大;当β＞1时,α=2的定位误差曲线却比实际噪声衰减系数曲线小。因此,在对目标进行定位之前,应对测试环境的噪声衰减系数进行测量。若α＜2,按实际噪声衰减系数进行求解;当α≥时,噪声衰减系数应当取值为2.

2.2 无线传声器阵列模型

4个节点可组成的图形有线型、圆形和四边形(三角形可看作四边形的一种特例)。由计算可知,当阵列形状为线型以及圆形时,(1)式无解。任意不在同一条直线上的四节点模型可视为圆上3点和圆内或圆外上的1点。因此,将无线四节点声阵列模型的3点固定于圆上,通过改变另外一点的位置来研究阵列形状对定位精度的影响。无线四节点声阵列模型如图3所示。

2.2.1 R、a对定位精度的影响

由于模型参数较多,根据控制变量法,将圆内三角形设为等边三角形,节点2坐标为(Rcos 0°,Rsin 0°),节点3坐标为(Rcos 120°,Rsin 120°),节点4坐标为(Rcos 240°,Rsin 240°).目标方位设为(50cos 30°,50sin 30°),声音衰减系数α=2.通过仿真可知,当a≤R时,定位误差较大。在a=R时甚至出现无解的情况。因此仿真过程中,将a设为4～10 m,所以,当R取2 m和3 m时,节点1在不同角度下的仿真结果如图4所示。

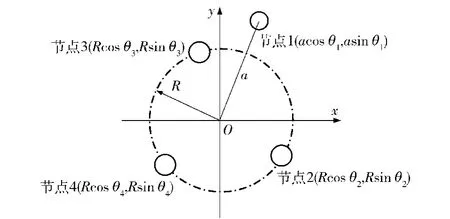
图3 四节点无线声传感器阵列模型Fig.3 Model of four-node wireless acoustic array

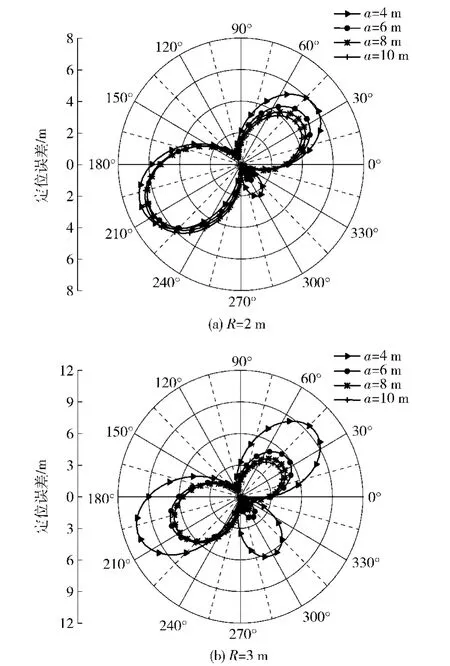
图4 节点1在不同位置时定位误差仿真结果Fig.4 Simulated results of location error of node 1 in different positions

图4的极径表示误差值,极角表示节点1的变换角度。由图4可知:a值越大,误差值越小。对比图4(a)和图4(b)可知:R值越小,误差值越小。但是,根据实际WSN的部署情况和节点密度的不同,R与a的取值也受到限制,本文取R=2 m,a=10 m.

2.2.2 目标声源与阵列的相对位置

由2.1节仿真结果可知,目标方位的变化对无线声传感器阵列的定位效果有很大的影响。为了避免阵列与目标声源处在定位误差较大的相对位置上,需研究目标声源与阵列的相对位置对定位精度的影响。在仿真过程中,取R=2 m,a=10 m,目标距离圆心50 m,目标方位角为θ.当节点2、节点3和节点4分别组成等边三角形、直角三角形和钝角三角形,目标方位角θ取0、π/4 rad、π/2 rad和3π/4 rad时,节点1在不同角度定位误差的仿真结果如图5所示。

对比图5(a)～图5(c)可以看出:圆内三角形形状随着目标声源位置的不同所产生的误差趋势是一致的,说明三角形的形状对定位误差影响不大。通过图5(a)～图5(c)还可分别看出:随着目标声源的方位变化,定位误差随节点1位置的变化的曲线相差较大。没有一种阵列模型能够使全向的目标定位精度达到最佳。但是,当节点1方向与目标声源方向夹角为60°～100°时,定位误差达到最小值。基于上述分析,为了方便实验进行,并根据实际研究的项目,本文提出Y型无线声传感器阵列,如图6所示。当目标声源在50 m的距离上360°变换时,仿真出该模型的定位误差,如图7所示。由图7可以看出,当目标声源的方位角在60°～100°和260°～300°时,定位误差＜1 m.在实际的节点选择过程中,没有必要一定选取Y型无线声传感器阵列,只需要满足半径R尽可能小,距离a尽可能大,并且节点1的方向与目标声源方向夹角60°～100°.

3 节点选择算法

WSN自组织目标定位算法的核心是在大量节点中选择合适的节点[15],从而使所提出的四节点无线声传感器阵列的定位算法达到最佳定位精度。本文WSN的各节点位置已知,并采用集中式处理模式,即所有数据处理都可在网关节点上进行。因此在网关节点上可把WSN看成是分布在以网关节点为中心、χ轴指向东、y轴指向北的直角坐标系中。当某一节点接收到的信号强度达到阈值时,唤醒周边其他节点,并在网关节点上运行节点选择算法。根据第2节仿真分析结果,节点选择可通过3个步骤实现,如图8所示。

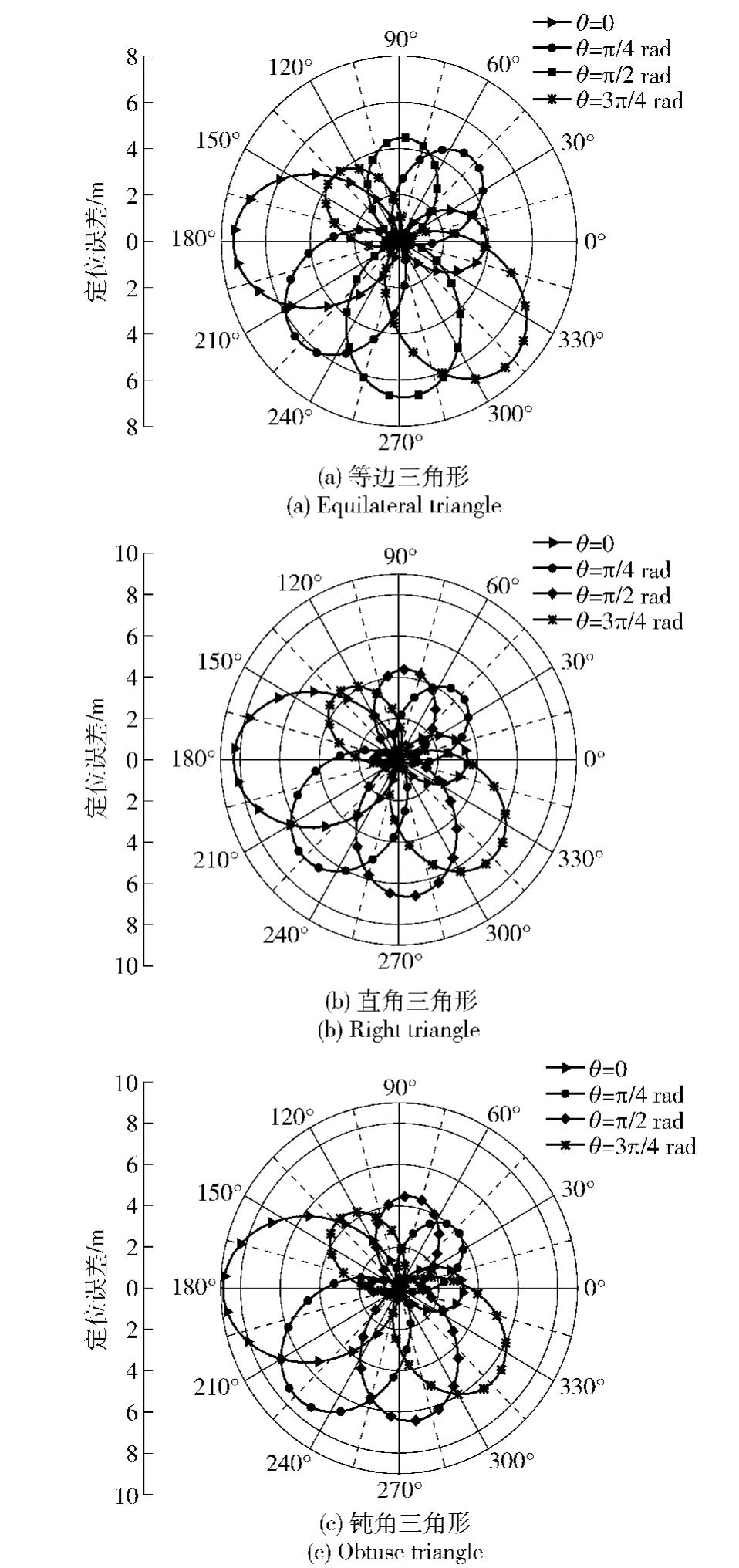
图5 圆上3点不同形状时定位误差仿真结果Fig.5 Simulated results of location errors with different forms in the circle

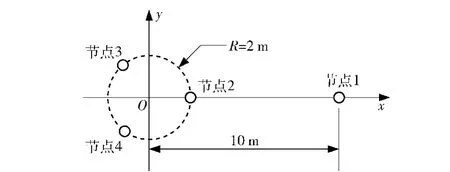
图6 Y型无线声传感器阵列模型Fig.6 Model of Y-type wireless acoustic array

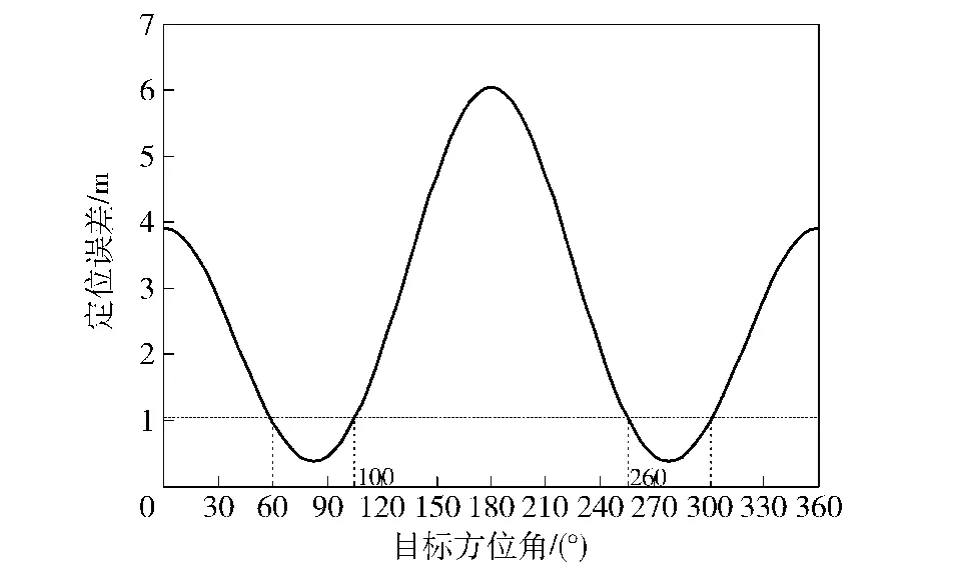
图7 Y型阵列模型目标定位误差Fig.7 Location error of Y-type array

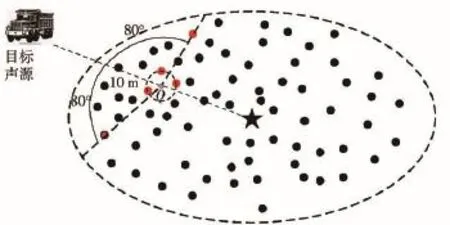
图8 节点选择算法示意图Fig.8 Schematic diagram of node selection algorithm

1)通过贪婪搜索算法确定接收能量最大的传感器节点[4],并以该节点与网关节点的连线作为目标的初始估计方向,如图8中点画线所示。

2)在以Q点为圆心,2 m为半径的圆上随意选择3个节点,作为四元无线声阵列的从节点。其中,Q为初始估计方向上距边界10 m的点。

3)以Q为起点,在80°方向选择距Q点10 m的主节点。图8中,上下两个80°方向可随意选择一个。

由于目标声源相对于阵列轴线的方位角在60°～100°和260°～300°时,阵列定位误差最小。且初步估计的目标方向误差较大,因此选择80°的偏转角度来确定主节点,从而留有余量容忍初步估计的目标方向误差。在节点选择过程中,可优先按照实际项目确定初始选择方案,如果并没有合适的四节点阵列,可以修改阵型参数,以得到更优或次优的定位结果,从而增加四元无线声阵列的适应性。

当无线声传感器阵列确定后,主节点负责收集其他3个节点的信息,计算出目标的方位。WSN区域外目标自组织定位过程如图9所示。

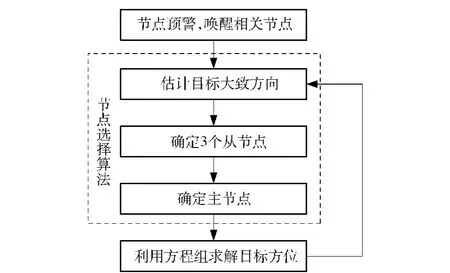
图9 WSN区域外自组织定位流程图Fig.9 Flow chart of self-organizing localization outside WSN

由于目标必须在与阵列轴线较为垂直的位置上,使得单个无线四元声阵列的适应性极低。但是,有别于传统的固定声阵列,在WSN中可通过选择不同的节点,得到不同形状、位置、大小的无线声阵列,不同的目标可根据角度的约束条件选择与之对应的声阵列。可简单地认为,WSN中存在无线声阵列的集合,每个不同时刻、不同位置的目标都能在集合中寻找到合适的无线声阵列。因此对于单个无线声阵列是缺乏普遍性的,WSN具有的声阵列集合弥补了这一缺陷。因此,WSN可根据目标的位置不断的更新声阵列,从而实现对运动目标的跟踪。

4 传感器节点设计及目标定位实验

4.1 四元无线声传感器阵列

在最佳四节点阵列模型被选择出来后,节点单元主要是通过声传感器采集目标信号进行实时处理。主节点在负责信号采集的同时,还需通过无线通讯方式收集其他节点信息,最后利用多路数据的算法融合实现对声源的定位估计。传感器节点电路主要包括信号采集模块、信号调理模块、信号处理模块、无线通讯模块和电源模块,如图10所示。

图10 传感器节点实物图Fig.10 Photograph of sensor node

4.2 声音衰减系数测试实验

在距声源154 m范围内,每隔1 m对信号进行采集,对采集的数据作短时能量处理,将处理后的数值通过Origin进行曲线拟合。在拟合工具中,选择Power幂函数方程进行拟合,Power幂函数方程的表达式为拟合后的曲线如图11所示,其中a= 657,b=2.14,因此实验环境下的声音衰减系数为2.14.由第3节的仿真分析可知,当噪声衰减系数大于2时,(1)式按衰减系数为2计算的结果误差更小,因此本文取α=2.

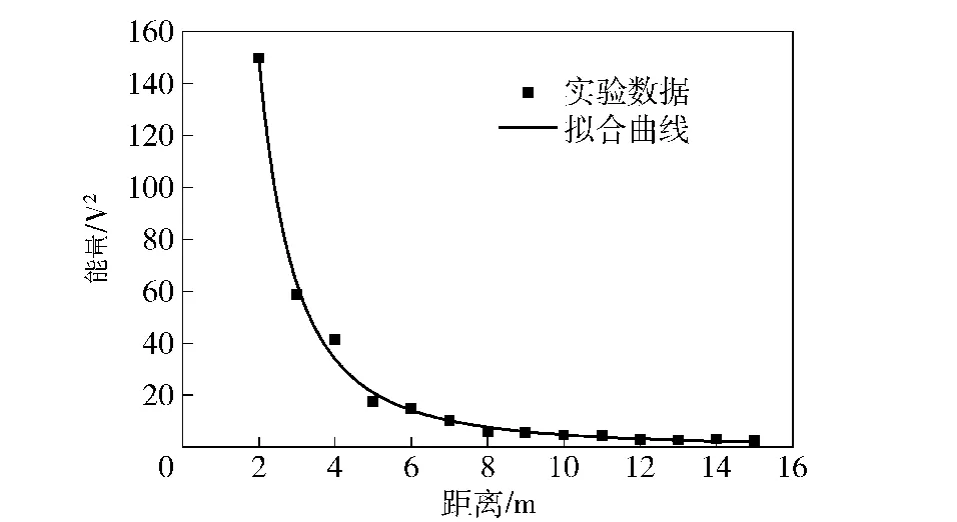
图11 噪声衰减系数拟合图Fig.11 Fitting chart of attenuation coefficient

4.3 Y型四元无线声传感器阵列目标定位实验

根据上文仿真分析,选择实录的坦克行进声音作为声源,按照Y型阵列摆放传感器节点,阵列中轴线与目标声源的夹角为80°,如图12所示。模型所涉及到的参数包括半径R和节点1到圆心的距离a.图13为a=8 m、R=2 m时Y型阵列各节点采集的波形图。

图12 Y型无线声传感器阵列目标定位实验场景图Fig.12 Experimental scene of source localization by Y-type array

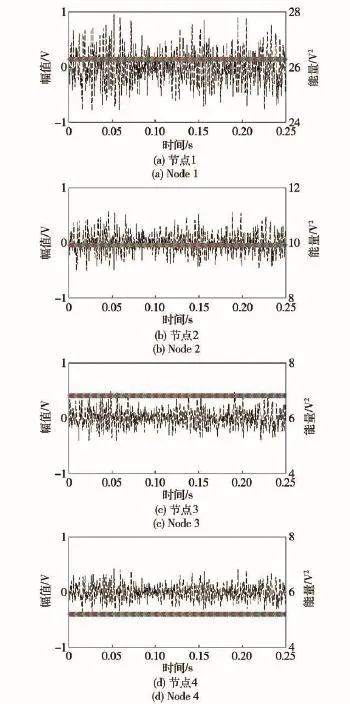
图13 a=8 m、R=2 m时各节点采集波形图Fig.13 Oscillograms of different nodes for a=8 m and R=2 m

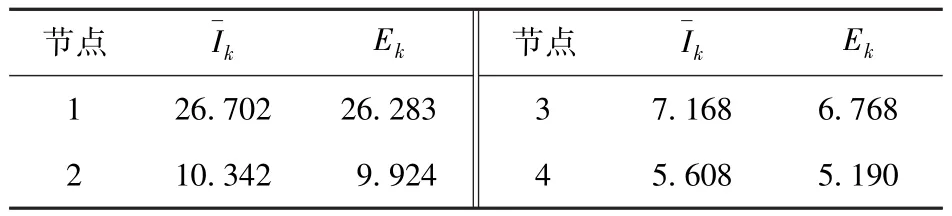
表1 a=8 m、R=2 m时Y型阵列各节点接收能量Tab.1 Received energies of nodes in Y-type array V2

将表1中Ek的数值和各节点的坐标位置信息代入方程组计算,得到定位误差大小为0.469 m.

改变Y型阵列半径R和节点1距圆心距离a,验证参数R和a的对阵列定位精度的影响。R分别取1.0 m、1.5 m和2.0 m,a分别取4 m、6 m和8 m.表2为不同参数下Y型阵列定位误差比较。

表2 不同参数下Y型阵列定位误差比较Tab.2 Location errors of Y-type array with different parameters

由表2可知,Y型阵列半径R越小,节点1距离圆心距离a越大的模型的定位精度越高。由实验数据可知,如果在WSN中选择了合适的四元无线声阵列,目标定位误差可被控制在1 m左右理想范围内,从而满足WSN抛撒区域外50 m处目标定位的精度要求。

5 结论

本文针对WSN抛撒区域外目标的定位问题,提出了四元无线声传感器阵列定位算法。分析了影响定位算法精度的两个误差源,声音衰减系数和四元阵列模型。当测试环境中的声音衰减系数和理论值进行比较时,衰减系数应选取小于等于2的数值进行计算。利用控制变量法对构成四元阵列模型的各参数进行了仿真,提出了Y型阵列,当Y型阵列中轴线与目标声源夹角为60°～100°时,定位误差小于1 m.在上述仿真的基础上,提出了四元无线声传感器阵列节点选择算法并进行了Y型阵列目标定位实验,实验结果表明,所提出的四元无线声阵列模型和定位算法能够满足WSN抛撒区域外50 m处目标的预警需求。

References)

[1]于振华,付晓,王静,等.基于声学无线传感器网络的目标跟踪系统研究[J].电子科技大学学报,2011,40(4):568-572.YU Zhen-hua,FU Xiao,WANG Jing,et al.On target tracking based on acoustic wireless sensor networks[J].Journal of University of Electronic Science and Technology of China,2011,40 (4):568-572.(in Chinese)

[2]张丽霞,汪文勇,李炯.无线传感器网络的目标定位问题研究[J].电子科技大学学报,2006,35(2):239-241.ZHANG Li-xia,WANG Wen-yong,LI Jiong.Research of object location by wireless sensor network[J].Journal of University of Electronic Science and Technology of China,2006,35(2):239-241.(in Chinese)

[3]夏娜,倪成春,徐朝农,等.逆向捕获时间差的 Voronoi声源定位机制[J].通信学报,2013,34(11):140-152.XIA Na,NI Cheng-chun,XU Chao-nong,et al.Voronoi acoustic source localization mechanism based on counter captured time difference[J].Journal of Communications,2013,34(11): 140-152.(in Chinese)

[4]Zhang J S,Walploa M,Roelant D,et al.Self-organization of unattended wireless acoustic sensor networks for ground target tracking [J].Pervasive and Mobile Computing,2009,5(2):148-164.

[5]Nakamura K,Nakadai K,Asano F,et al.Intelligent sound source localization and its application to multimodal human tracking[C]//Proceedings of 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS).San Francisco,US:IEEE,2011:143-148.

[6]陈旿,孙建华,于振兴,等.基于IEEE1588的无线传感器网络时钟同步方法[J].系统工程与电子技术,2014,36(3): 564-574.CHEN Wu,SUN Jian-hua,YU Zhen-xing,et al.Clock synchronous method for wireless sensor networks based on IEEE 1588[J].Systems Engineering and Electronics,2014,36(3):564-574.(in Chinese)

[7]王义君,钱志鸿,王桂琴,等.无线传感器网络能量有效时间同步算法研究[J].电子与信息学报,2012,34(9):2174-2179.WANG Yi-jun,QIAN Zhi-hong,WANG Gui-qin,et al.Research on energy-efficient time synchronization algorithm for wireless sensor networks[J].Journal of Electronics&Information Technology,2012,34(9):2174-2179.(in Chinese)

[8]Cheng L,Wu C D,Zhang Y Z,et al.A survey of localization in wireless sensor network[J].International Journal of Distributed Sensor Networks,2012,4(1):1-12.

[9]Meng W,Xiao W D,Xie L H.An efficient EM algorithm for energy-based multisource localization in wireless sensor networks[J].IEEE Transactions on Instrumentation and Measurement,2011,60(3):1017-1027.

[10]Ampeliotis D,Berberidis K.Low complexity multiple acoustic source localization in sensor networks based on energy measurements[J].Signal Processing,2010,90(4):1300-1312.

[11]Sheng X H,Hu Y H.Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks[J].IEEE Transactions on Signal Processing,2005,53(1):44-53.

[12]朱明强,侯建军,刘颖,等.基于自适应比例修正无迹卡尔曼滤波的目标定位估计算法[J].兵工学报,2013,34(5): 561-566.ZHU Ming-qiang,HOU Jian-jun,LIU Ying,et al.Target locating estimation algorithm based on adaptive scaled unscented Kalman filter[J].Acta Armamentarii,2013,34(5):561-566.(in Chinese)

[13]崔晓宗,仝杰,刘弢,等.一种用于无线传感器网络的非线性最小二乘声源定位算法[J].计算机研究与发展,2011,48(S):65-70.CUI Xiao-zong,TONG Jie,LIU Tao,et al.A nonlinear least square acoustic source localization algorithm for wireless sensor networks[J].Journal of Computer Research and Development,2011,48(S):65-70.(in Chinese)

[14]Blatt D,Hero A Q.Energy-based sensor network source localization via projection onto convex sets[J].IEEE Transactions on Signal Processing,2006,54(6):36143619.

[15]陈积明,张艳平,曹向辉,等.基于声强的无线传感器网络目标跟踪方法研究[J].电子与信息学报,2009,31(11): 2791-2794.CHEN Ji-ming,ZHANG Yan-ping,CAO Xiang-hui,et al.A-coustic energy based scheme for target tracking in wireless sensor networks[J].Journal of Electronics&Information Technology,2009,31(11):2791-2794.(in Chinese)

Node Selection and Source Localization of Four-node Wireless Acoustic Array in Wireless Sensor Network

ZHU Hai-yang,ZHANG He,MA Shao-jie,PAN Han
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

Instead of using microphone array,each sensor node in the sensor network uses only a single microphone as its sensing device in low-cost and miniature wireless acoustic sensor network(WASN).According to the energy decay model and geometric positioning mechanism,an external acoustic source localization estimation method with four-node wireless microphone array is presented for the application in randomly deployed WASN.Major error sources,such as sound attenuation coefficient and array shape,of the localization method are analyzed,and Y-type array model is selected as sensing model.The location error is less than 1m when the angle between the central axis of Y-type array and the target is 60°～100°.A node selection algorithm is proposed,and the experiment of source localization is done.The experimental result shows that Y-type wireless acoustic array can warn about target at 50m away from the wireless sensor network(WSN).

ordnance science and technology;wireless acoustic sensor network;four-node wireless acoustic array;node selection;source localization

TN915.5

A

1000-1093(2016)01-0083-08

2015-05-05

朱海洋(1989—),男,博士研究生。E-mail:njustzhu@163.com;张合(1957—),男,教授,博士生导师。E-mail:hezhangz@mail.njust.edu.cn