基于MATLAB的警用无人战车动力学建模与仿真

商保利　战仁军　商　鹏

1(中国人民武装警察部队工程大学研究生管理大队　陕西 西安 710086)2(中国人民武装警察部队工程大学装备工程学院　陕西 西安 710086)



基于MATLAB的警用无人战车动力学建模与仿真

商保利1战仁军2商鹏2

1(中国人民武装警察部队工程大学研究生管理大队陕西 西安 710086)2(中国人民武装警察部队工程大学装备工程学院陕西 西安 710086)

为了研究无人战车在受到后坐力冲击和路面随机激励的响应情况下，确保战车行驶的平顺性和武器射击的稳定性。根据振动力学理论建立了四自由度的战车动力学模型，利用系统微分方程求解系统的固有频率及主振型，并提出基于MATLAB语言的车辆动力特性的快速计算方法，得到战车在不同振动模式下对(前—后)轮激励的频率函数。结果表明，二阶固有频率对车体俯仰运动的影响最大。结果为设计人员提供了避免共振的理论依据，也为分析系统的解耦提供依据。

固有频率主振型频率响应无人战车

0　引　言

无人战车是一款由遥控驾驶并携带非致命性武器执行处突反恐任务的武器载体，可以用来搭载防暴弹发射器、激光炫目器、声波武器等多种非致命武器。由于武器对射击精度有一定的要求，那么保证战车行驶的平稳性尤为重要，而战车行驶的平稳性主要与其动力学特性有关。因此，我们根据振动力学的理论构建战车的动力学模型。

1　构建战车动力学模型

无人战车系统主要四个由轮毂电机、独立悬架、车架、车壳以及车上装载的武器构成。采用轮毂电机，减小了由于发动机振动带来的车体振动响应，但与此同时由于轮毂电机的质量较重，增加了非簧载的质量，势必会导致车的动力性能发生变化。车体的动力学特性主要与四个独立悬架和轮胎的特性有关，我们主要研究车体的俯仰运动对射击稳定性的影响，因此我们根据振动力学理论建立1/2车体系统的四自由度振动模型[1，2]，如图1所示。

图1　1/2战车四自由度振动系统模型

在表1中，我们给定了各符号的物理意义。

表1　符号表

基于拉格朗日法[3]，系统的运动微分方程可表达为:

其中，质量矩阵M为对角阵，阻尼矩阵C与刚度矩阵K为实对称阵，Y为坐标向量，即:

2　系统固有模态的求解

2.1求解固有频率及主振型的解析方法

由于阻尼不会影响系统的固有频率，在求解固有频率的时候，我们可以忽略阻尼，把系统看成一个保守系统,即阻尼矩阵C= 0[4]。为求解4自由度系统的4阶固有频率，设系统的固有频率的平方为系统特征矩阵的特征值。系统的特征矩阵可表示为:

A=K-ω2M

代入表2中的数据。

表2　系统物理与几何参数表

解得系统的4阶固有频率为:ω1=7.682,ω2=38.92,ω3=114.75,ω4=114.90 rad/s。

设系统的主振型为：

当ω1 = 7.682 rad/s时，求解线性方程组：

其解为第一个主振型:

同理，当ω2 = 38.92，ω3 =114.75，ω4=114.90 rad/s时，可求得余下三个主振型:

振型如图2所示。从振型图中我们可以看出，一阶振型为车体正向刚体平动，二阶振动为车体逆时针刚体转动，三阶振型为车轮正向刚体平动，四阶振型为车轮反向刚体平动。二阶振动时车体产生的转动最为明显，因而对防暴弹发射精度的影响最大。因此在发射时要避开二阶固有频率，避免共振的产生。

图2　1/2车体4自由度振型图

2.2固有频率及主振型的仿真方法

调用[Q,d]=eig(inv(M)×K)函数求解，其中生成的矩阵Q为各列主振型，d的对角元素为系统的固有频率的平方。编写程序如下：[5]

clc

clear all

close all

format long

%Initial

mv=1000;

J=900.84;

mb=30;

mf=30;

kbs=31000;

kfs=31000;

kbw=364000;

kfw=364000;

cbs=2784;

cfs=2784;

cbw=1497;

cfw=1497;

lb=1.6;

lf=1.4;

M=diag([mv,J,mf,mb]);

Kt=[0,0;0,0;kfw,0;0,kbw];

Ct=[0,0;0,0;cfw,0;0,cbw];

K=[kfs+kbs,-lf*kfs+lb*kbs,-kfs,-kbs;-lf*kfs+lb*kbs,lf^2*kfs+lb^2*kbs,lf*kfs,-lb*kbs;

-kfs,lf*kfs,kfs+kfw,0;

-kbs,-lb*kbs,0,kbw+kbs];

C=[cfs+cbs,-lf*cfs+lb*cbs,-cfs,-cbs;-lf*cfs+lb*cbs,lf^2*cfs+lb^2*cbs,lf*cfs,-lb*cbs;

-cfs,lf*cfs,cfs+cfw,0;

-cbs,-lb*cbs,0,cbw+cbs];

[Q,d]=eig(inv(M)*K)

由仿真结果得到系统的固有频率如下：

f1=7.530f2=37.89f3=114.76f4=114.80

对应的主振型分别为:

得到的结果与解析结果近似相同。

3　求解系统频率响应函数

3.1系统频率响应函数数学解法

一般粘性有阻尼多自由度系统振动方程写成一般式的形式为[6]:

对公式两边进行拉普拉斯变换：

[Ms2+Cs+K]X(s)=[Kt+Cts]Q(s)

得到传递函数矩阵:

以jw代替s算子，就可以得到振动的频率响应函数矩阵：

H(jw)=[K-Mw2+jwC]-1[Kt+jw·Ct]

频率响应函数矩阵H(jw)由频率函数矩阵组成：

其中，H11(w)是车身垂直振动对前轮激励的频率响应函数，H12(w)是车身垂直振动对后轮激励的频响函数；H21(w)、H22(w)分别为车身俯仰振动对前后轮激励的频响函数；H31(w)、H32(w)分别为前轴振动对前后轮激励的频响函数；H41(w)、H42(w)分别为后轴振动对前后轮激励的频响函数[7]。

3.2系统频率响应函数仿真解法

%频率响应函数

syms w

h1=(-w*w).*M+(i*w).*C+K; %频响函数

h2=inv(h1);

h3=Kt+(i*w).*Ct;

h4=h2*h3;

h4(1,1);%车身垂直振动对前轮激励的频率函数

h4(1,2);%车身垂直振动对后轮激励的频率函数

h4(2,1);%车身俯仰振动对前轮激励的频率函数

h4(2,2);%车身俯仰振动对后轮激励的频率函数

h4(3,1);%前轴振动对前轮激励的频率函数

h4(3,2);%前轴振动对后轮激励的频率函数

h4(4,1);%后轴振动对前轮激励的频率函数

h4(4,2);%后轴振动对后轮激励的频率函数

w1=1:1:100;

figure(1),

h61=subs(h4(1,1),w,w1);

h62=subs(h4(1,2),w,w1);

plot(w1,h61,w1,h62);

grid on

title(′车身垂直振动对(前—后)轮激励的频率函数′);

figure(2),

h63=subs(h4(2,1),w,w1);

h64=subs(h4(2,2),w,w1);

plot(w1,h62,w1,h64);

grid on

title(′车身俯仰振动对(前—后)轮激励的频率函数′);

figure(3),

h65=subs(h4(3,1),w,w1);

h66=subs(h4(3,2),w,w1);

plot(w1,h65,w1,h66);

grid on

title(′前轴振动对(前—后)轮激励的频率函数′);

figure(4),

h67=subs(h4(4,1),w,w1);

h68=subs(h4(4,2),w,w1);

plot(w1,h67,w1,h68);

grid on

title(′后轴振动对(前—后)轮激励的频率函数′);

最后得到车身的频率响应函数如图3-图6。

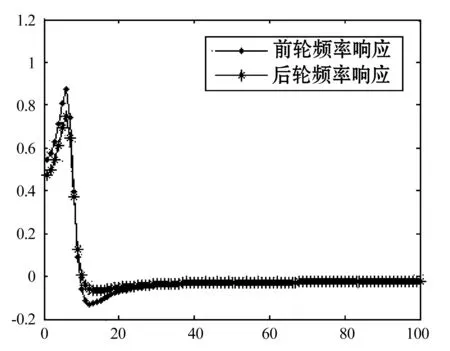
图3　车身垂直振动频率响应曲线

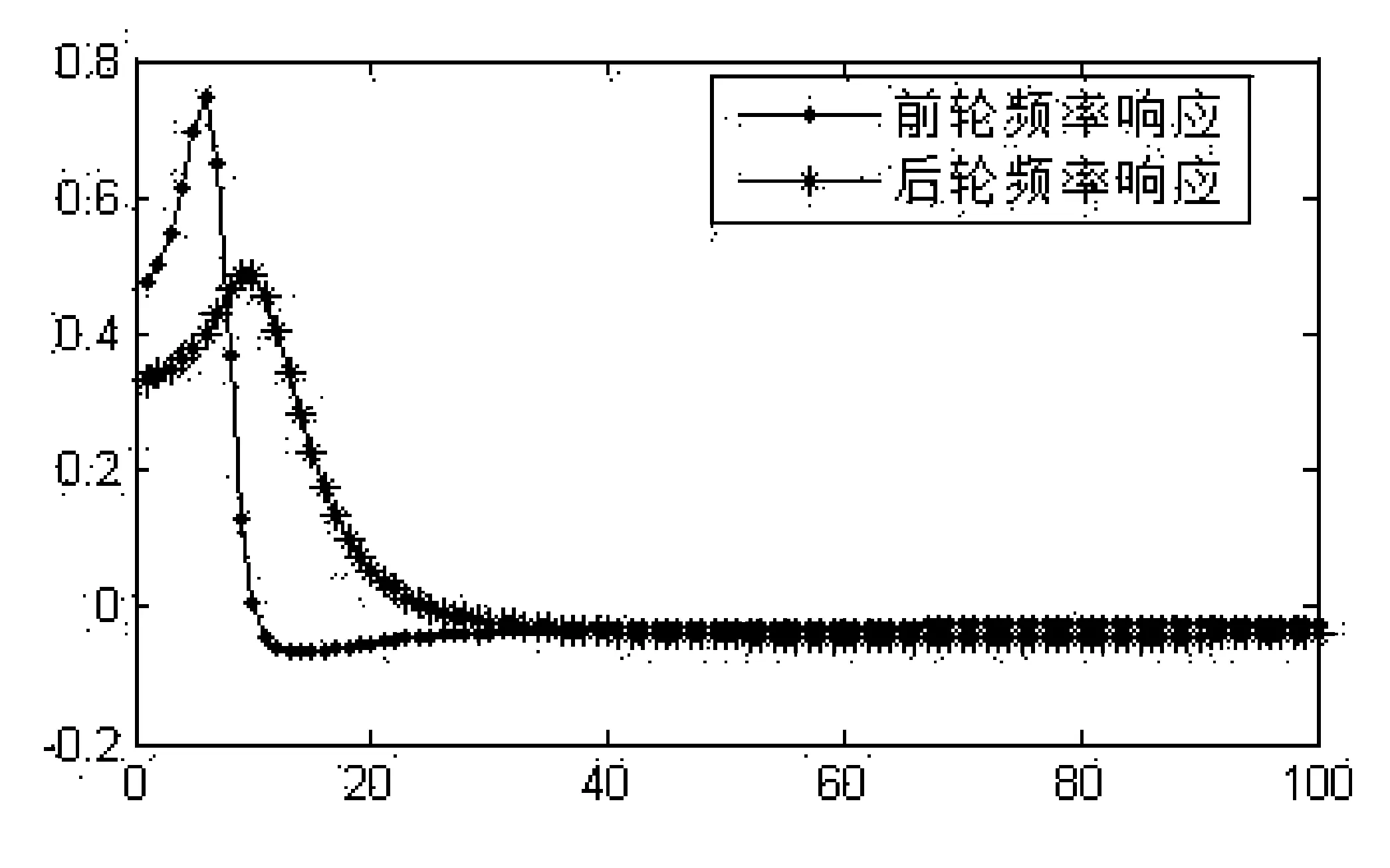
图4　车身俯仰振动频率响应曲线

图5　前轴振动频率响应曲线

图6　后轴振动频率响应曲线图

4　结　语

本文利用振动力学理论，建立了无人战车四自由度的振动模型，通过求解运动微分方程，得到战车系统的固有参数。同时为同类其他车载武器的动力响应求解提供了方法的借鉴。

(1) 提供求解系统的固有频率和主振型的数学解法及仿真解法。从结果可以看出，二阶固频对车体俯仰运动的影响最大，因此发射模式或者路面不平所带来的外力激励的频率要尽量避开这四阶固有频率，来避免由于共振所带来的机械损坏以及对射击精度的影响。

(2) 提供求解系统频率响应函数的数学解法及仿真解法。从图3和图4可以看出，前后轮在激励频率为7～9范围内极易发生共振[8]。前轮的垂直振动和俯仰振动的幅度比后轮幅度稍大；从图5和图6可以看出，由于前后悬架的型号一致，前轴振动和后轴振动引起的频率响应非常相似。其中，前轴振动对前轮的影响较大，后轴振动对后轮的影响较大。

[1] 王良曦，王红岩.车辆动力学[M].北京：国防工业出版社,2008.

[2] 谢官模.振动力学[M].北京：国防工业出版社,2011.

[3] William T Thomson,Marie Dillon Dahleh.Theory of Vibration with Application [M].5th Ed.Englewood Cliff： Prentice Hall,1997.

[4] 全顺喜，王平，赵才有.车辆多体系统振动方程建立探讨[J].振动与冲击，2013,32(11):173-177.

[5] 余胜威.MATLAB车辆工程应用实战[M].北京:清华大学出版社，2014.

[6] Singiresu S Rao.机械振动[M].4版.李欣业,张明路,译.北京：清华大学出版社,2009.

[7] 李红波,薛亮,吴渝,等.展示车辆平顺性的虚拟仿真技术[J].计算机工程与设计，2012,33(10):3918-3922.

[8] 刘云，钱振东.路面平整度及车辆振动模型的研究综述[J].公路交通科技，2008,25(1):51-57.

KINETIC MODELLING AND SIMULATION OF UNMANNED COMBAT VEHICLES BASED ON MATLAB

Shang Baoli1Zhan Renjun2Shang Peng2

1(Group of Graduate Students,Armed Police Engineering University，Xi’an 710086，Shaanxi,China)2(CollegeofEquipmentEngineering,ArmedPoliceEngineeringUniversity，Xi’an710086，Shaanxi,China)

In order to study the response situation of unmanned combat vehicles on the impact of recoil shock and the random roads excitation and to ensure the ride comfort of combat vehicle driving and the stability of weapons firing,according to the vibration mechanics theory,we built a kinetic model of combat vehicle with four freedom degrees,used the system differential equations to calculate natural frequency and main vibration mode of the system,and proposed a MATLAB language-based fast calculation method of kinetic characteristics of vehicles,got the frequency function of excitation exerted by vehicles on (front and rear) wheels in different vibration modes.Results told that the second-order natural frequency has the greatest effects on vehicle body’s pitching motions.These results provide theoretical basis for the designer to avoid resonance,as well as the basis for analysing system decoupling.

Natural frequencyMain vibration modeFrequency responseUnmanned combat vehicle

2015-04-10。商保利，硕士生，主研领域：军事装备建模与仿真。战仁军，教授。商鹏，助教。

TP391.9

A

10.3969/j.issn.1000-386x.2016.09.020