探地雷达衰减补偿逆时偏移成像方法

朱尉强， 黄清华

北京大学地球与空间科学学院地球物理学系, 北京　100871



探地雷达衰减补偿逆时偏移成像方法

朱尉强， 黄清华*

北京大学地球与空间科学学院地球物理学系, 北京100871

探地雷达信号在地下介质中传播时易受到电导率所产生的衰减影响，从而使得传统偏移成像结果在高衰减区域变得模糊.本文提出了衰减补偿的逆时偏移方法来消除电导率的影响.该方法基于麦克斯韦方程组实现电磁波的正演模拟和逆时传播.通过改变衰减项的正负号，保证了逆时传播的时间对称性，从而能够重构出原始波场，实现衰减补偿.数值实验比较了传统逆时偏移方法和衰减补偿逆时偏移方法在存在高导异常区域情况下的成像效果，结果证明了衰减补偿逆时偏移方法能够很好地恢复由电导率造成的信号衰减，从而提高探地雷达剖面的分辨率.关键词探地雷达; 衰减补偿; 逆时偏移

1　引言

探地雷达是基于高频电磁波对浅层地下介质信息进行探测的有效手段.由于电磁波与地震波间的相似性，地震数据处理方法被广泛地运用于探地雷达数据的处理中，例如偏移成像技术(Fisher et al., 1992; Leuschen et al., 2001; Radzevicius 2008; Liu et al., 2014).但是这些探地雷达偏移方法都未考虑衰减的影响.对于电磁波而言，电导率的存在会造成振幅的衰减，从而导致在相对高导区域无法得到清晰的偏移成像结果，例如污水泄露区域，海水侵入环境等(Heteren et al., 1998; Sauck et al., 1998).电磁波的这一特点使得电导率成为探地雷达数据处理中必需考虑的因素.

对于探地雷达数据中的波形衰减效应的研究目前主要有两个方面：衰减的估计和衰减的补偿.Turner et al.,(1994)与 Bradford (2007)提出了用Q值函数来描述探地雷达衰减效应.Turner (1994)与 Irving et al.(2003)借鉴地震学中的反Q滤波技术讨论了对于探地雷达数据的Q值估计和反Q滤波方法，经过反Q滤波后的数据被进一步用于偏移成像.张先武等(2014)通过地下介质等效滤波器的振幅谱来求取反滤波器并对探地雷达数据进行反滤波处理消除衰减效应.但是反滤波方法使用了一维的衰减模型，因而无法考虑复杂的地质条件.在偏移成像过程中考虑衰减补偿则可适用于更为复杂的模型.电磁波的衰减发生于波场传播过程，而偏移成像基于波场对时间的反向延拓，在此过程中同时考虑衰减的补偿可以增强高衰减区域的信号强度，改善成像效果.现有的考虑衰减补偿的探地雷达偏移方法都为频率域方法(Bano 1996; Bitri et al., 1998; Sena et al., 2006; Oden et al., 2007)，此类方法将衰减效应作为复数波速的虚部进行补偿.底青云等(2000)提出了基于2D有限元方法的GPR 偏移方法，考虑了电导率对于速度的影响，但未修正振幅的衰减.

逆时偏移方法是勘探地震学中针对复杂地下结构的非常有效的偏移成像方法(Yoon et al., 2003; Etgen et al., 2009).该方法也被有效地应用于探地雷达的数据处理中(Fisher et al., 1992; Leuschen et al., 2001; 雷林林等, 2015)，但之前的工作中都未考虑电导率的影响.借鉴勘探地震学中Q-RTM(Q-compensated reverse-time migration)方法(Zhu et al., 2014; Zhu 2014)，本文提出了针对探地雷达的衰减补偿逆时偏移方法，通过改变衰减项的正负号保持了逆时传播的时间对称性，实现在逆时偏移过程中的衰减补偿.通过数值实验分析了不同逆时传播方式与重构波形之间的关系，验证了本文方法相比传统不考虑电导率的逆时偏移方法的优势.

2　方法

地下介质的电导率会对电磁波的振幅与速度都产生影响.考虑平面波垂直入射均匀介质的情况，设地表为xy平面，z轴垂直向下，根据麦克斯韦方程：

(1)

可以求出导体内部电场为

(2)

(3)

其中，E为电场分量，ω为角频率，μ为磁导率，ε为介电常数，σ为电导率.从方程(2)可以看出在电导率对速度(v=ω/β)与衰减项e-αz都有一定影响.图 1展示了不同电导率下，电磁波速度与振幅的变化，可以看到电导率主要造成电磁波振幅的衰减，而对速度的影响很小.当σ=0.01S·m-1，在深度1m处振幅已经衰减为地表振幅的54%，而速度相比没有电导率情况下仅减小约1%.由于电导率对于振幅的影响，对于存在高衰减区域的探地雷达剖面，衰减补偿成为必要的数据处理方法.

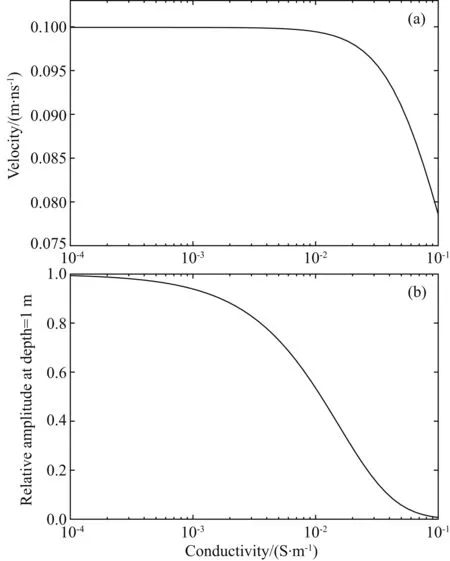
图1　电导率对电磁波速度和振幅的影响(a) 速度与电导率关系； (b) 相对振幅与电导率关系.地面电磁波振幅设为1.Fig.1　The effect of conductivity on velocity and amplitude(a) Relationship between velocity and conductivity; (b) relationship between relative amplitude and conductivity. The amplitude at surface is set as 1.

如果不考虑电导率项，电磁波方程与声波方程则具有相同的形式：

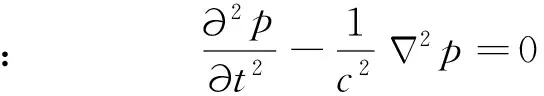
(4)

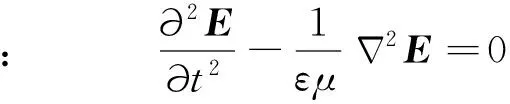
(5)

其中，p为压强，c为声速.因而，传统的探地雷达的逆时偏移方法都直接借鉴了勘探地震学中的逆时偏移方法.由于方程(4)与方程(5)仅仅与时间的二次导数相关，根据时间反转不变原则(Fink1992),如果p(x,t)为声波方程(4)的一个解，则p(x,-t)是同一问题的另外一个解.逆时偏移成像通过将接收信号时间反转 (t→-t)后作为边界条件重新注入计算区域，从而实现波场的重构，再通过成像条件提取出目标体的形态与位置(Kaelinetal., 2006).

但是对于包含电导率项的完整电磁波方程(方程(1))，存在对于时间的一阶导数，失去了时间反转不变性：

(6)

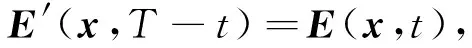
(7)

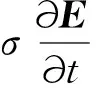
(8)

此时方程(8)与方程(1)在形式上完全一致，人为保持了时间的对称性.从而基于方程(8)的波场逆时传播可以完全重构原始波场，实现对于衰减的补偿.

3　数值算例

3.1逆时波场重构

为了验证逆时波场重构的效果，我们采用了图 2a所示均匀模型(εr=9,σ=0.01 S·m-1)进行验证.我们在图 2a中四个方向都放置了接收点(红色)，图中黄色星号为发射源.本文采用时间域有限差分方法(FDTD)来实现基于麦克斯韦方程的电磁波的模拟和逆时偏移.空间步长选为dx=dz=0.02 m，时间步长为dt=0.04 ns.激发信号采用了中心频率为100 MHz的ricker子波.图 2b为在模型中心点接收到的波形，展示了基于方程(6)与方程(8)下的逆时重构的波场间差别.图中蓝线(No.1)为正演时波形，即在黄色星号点处输入激发信号后记录到的波场.粉线(No.2)，绿线(No.3)，红色叉号(No.4)为逆时偏移时记录到的波形，即将图 2a中红色接收点接收到的信号经时间反转后作为边界条件注入计算区域后重构的波场.其中，粉线为不考虑电导率时(εr=9,σ=0 S·m-1)的逆时偏移结果，绿线为基于方程(6)的逆时偏移结果，红色叉号为基于方程(8)的逆时偏移结果.从图 2b可以清楚地看到，传统不考虑电导率的逆时偏移无法恢复电导率带来的衰减，基于方程(6)的逆时偏移方法引入了二次衰减，相比传统不考虑电导率方法在振幅上更加恶化了成像效果，而本文的衰减补偿逆时偏移方法则可以精确地进行波场重构，消除电导率带来的振幅衰减.

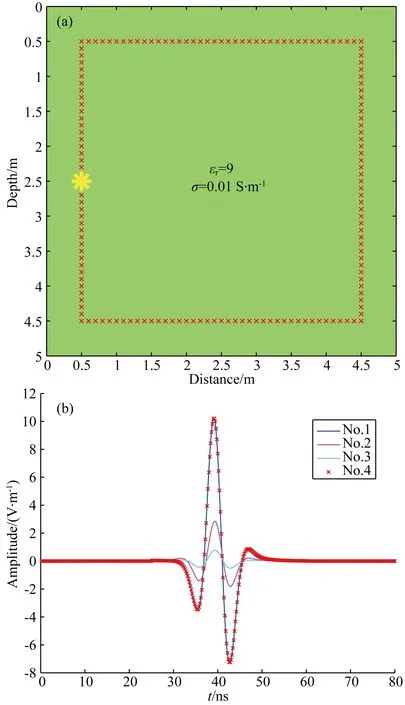
图2　(a) 测试电磁模型； (b) 不同逆时偏移方法重构的电磁波振幅.图2a中测试模型为均匀电磁模型(εr=9,σ=0.01 S·m-1)，黄色星号为发射源位置，红色叉号为接收点位置.波场的正演模拟和逆时传播都基于FDTD方法.图 2b中蓝线(No.1)为模型中心点记录到的正演模拟波形.粉线(No.2)，绿线(No.3)，红色叉号(No.4)为逆时传播时记录波形.其中，粉线为采用没有电导率模型(εr=9,σ=0 S·m-1)的逆时传播结果，绿线为基于方程(6)和图2a中模型的逆时偏移结果，红色叉号为基于方程(8)和图2a中模型的逆时偏移结果.Fig.2　(a) Test model; (b) Reconstructed waveform by different reverse time modeling methods. The test model in Fig.2a is a homogeneous model with εr=9,σ=0.01 S·m-1. The yellow star is the location of the source and the red crosses are the locations of the receivers. FDTD method is used for the forward and time-reverse modeling of electromagnetic wavefields. The blue line (No.1) in Fig.2a is the waveform recorded at the center of the model during forward modeling. The pink line (No.2), green line (No.3), red crosses (No.4) are the recorded waveform during time-reverse modeling. The pink line is the reconstructed waveform produced by a model without conductivity (εr=9,σ=0 S·m-1). The green line is the reconstructed waveform using eq. (4) and the model in Fig.2a. The red crosses are the reconstructed waveform using eq. (6) and the model in Fig.2a.

3.2污水渗漏模型

为了验证衰减补偿逆时偏移方法相对于传统不考虑衰减的逆时偏移方法的优势，我们首先设计了一个简单的三层模型(图3a):空气层(εr=1)，泥土层(εr=9)和含水层(εr=80).在均匀电导率背景模型(σ=0.001 S·m-1)中间存在一高导区域(σ=0.01 S·m-1)，模拟生活中存在污水渗漏情况(Chang et al., 2004).为了仅验证电导率的影响，我们只在电导率模型中放置了这一异常.高电导区域边界通过高斯平滑处理以避免在边界产生强烈反射.发射源间距为0.5 m,接受点间距为0.1 m.空间采样，时间采样，激发信号都与之前相同.一个均匀的相对介电常数模型(εr=9)和图 3b的电导率模型被用于逆时偏移成像.

为了比较衰减补偿逆时偏移方法的效果，我们首先对于不存在高电导率区域的模型进行了逆时偏移成像，结果如图4a所示.在没有高导异常影响情况下，界面可以被清晰地成像.然后我们针对存在高导异常的模型进行了传统不考虑电导率的逆时偏移(图4b)和衰减补偿逆时偏移(图4c).比较图4中成像结果，由于高电导率导致的波形衰减，高导异常区域内的界面信号被强烈衰减.通过衰减补偿逆时偏移后，电导率导致的波形衰减被有效恢复.

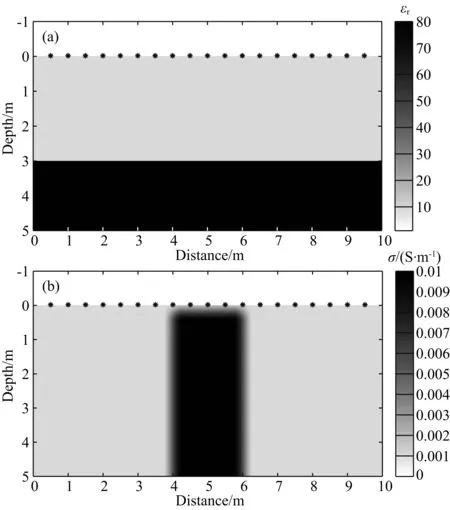
图3　污水渗漏模型(a) 相对介电常数(εr)模型； (b) 电导率(σ)模型.相对介电常数模型包括三层:空气层(εr=1)，泥土层(εr=9)和含水层(εr=80). 电导率模型背景为σ=0.001 S·m-1，中间具有存在一高导区域(σ=0.01 S·m-1)，模拟生活中存在污水渗漏情况.发射源与接收点都位于地面.图中星号为发射源位置，间距为0.5 m,接收点间距为0.1 m.Fig.3　Wastewater infiltration model(a) model of dielectric permittivity; (b) model of conductivity. The model of dielectric permittivity consists of three layers: air, unsaturated soil, saturated soil. The background of the conductivity model is σ=0.001 S·m-1. There is a high conductive anomaly zone in the center, which corresponds to an area contaminated by waste water. The sources and receivers are distributed on the surface. The asterisks are locations of sources with a spacing 0.5 m; and the spacing of receivers is 0.1 m.

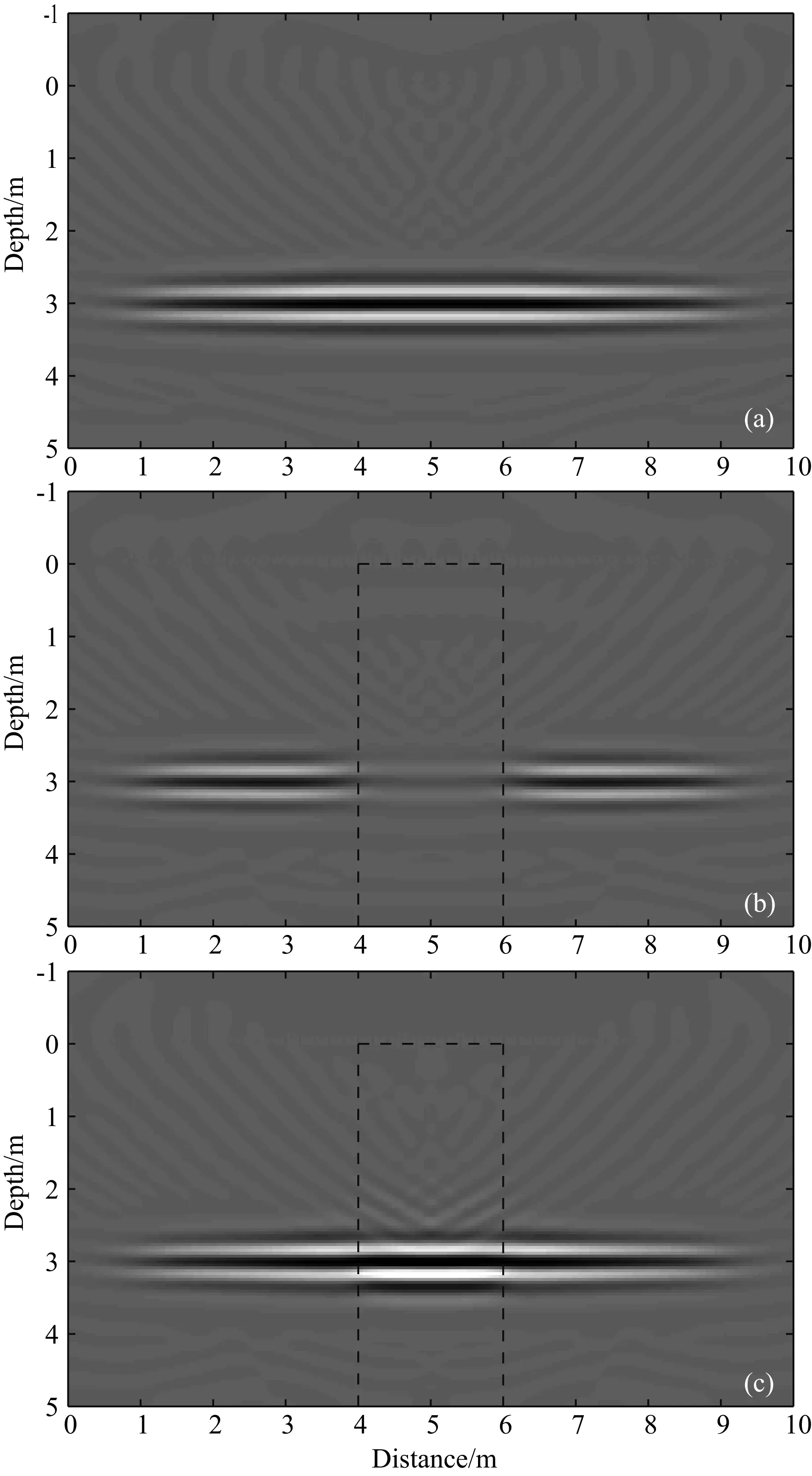
图4　污水渗漏模型逆时偏移结果比较(a) 原始模型不包含电导率异常下的偏移结果； (b) 高电导异常下传统不考虑电导率逆时偏移结果； (c) 高电导异常下衰减补偿逆时偏移结果.图(a)中逆时偏移结果是基于原始不含有电导率及相应波形衰减影响的模拟数据得到，作为参照结果.图(b)与图(c)中逆时偏移结果都是基于图 3模型的模拟数据得到.图(b)与图(c)中虚线为高导异常区域.Fig.4　Results of reverse time migration(a) Result using data without the conductivity anomaly; (b) result of conventional reverse time migration; (c) result of attenuation compensated reverse time migration. The result in Fig.4a which is for comparison is based on GPR data generated by a model without the conductivity anomaly. The results in Fig.4b and Fig.4c are based on GPR data generated by the model in Fig.3. The dashed lines in Fig.4b and Fig.4c show the locations of the high conductive anomaly zones.

3.3渗水断层模型

为了进一步说明衰减补偿逆时偏移方法在探地雷达中的应用前景，我们设计了一个渗水的断层模型(图5)，断层区域存在高电导率异常(σ=0.01 S·m-1，背景为σ=0.001 S·m-1).用于逆时偏移的模型通过对原始模型进行高斯平滑后得到(图6).发射源间距为0.3 m，接收点间距为0.1 m.空间采样，时间采样，激发信号都与之前相同.图7展示了传统不考虑电导率的逆时偏移和衰减补偿逆时偏移的结果.电磁波在经过断层内部时，由于电导率的存在会使波形受到衰减.如果在偏移中不考虑电导率的影响，断层内部及其下部界面的成像结果(图7中虚线方框区域)变得模糊.通过衰减补偿逆时偏移后，断层内部及其下部界面的成像结果都被显著改善.

3.4结果分析与讨论

以上数值模拟实验初步证明了本文采用的衰减补偿逆时偏移成像方法在存在高电导率影响的探地雷达数据处理中所起作用.

在理想的采集方式下(图2a)，即在源的四周都进行信号的采集记录，通过衰减补偿的逆时重构可以完全恢复原始的波场(图2b)，电导率造成的波形衰减被完全补偿.这与第二节中理论分析相符.对于实际的测量，理想的采集方式很难实现，我们往往只能在探测区域的一侧进行测量.但这并不影响逆时传播中对波形的补偿效果.之后的两个数值模型结果(图4与图7)也证实了这一点.

在污水渗漏模型中，传统的逆时偏移成像结果(图4b)会使高导异常区域内的信号变得较弱.在实际的数据中，如果存在一定噪声，并且存在更多数量、形态更加复杂的地下构造时就会对解释造成很大的困难.经过衰减逆时偏移成像后的界面信号强度与原始模型不包含电导率异常下的偏移结果相近，有效地消除电导率的影响，有利于数据的解释分析.

渗水断层模型虽然结构较为复杂，但是通过使用衰减补偿逆时偏移方法后仍然得到了很好的补偿效果.图7(b)与图7(a)都为施加互相关成像条件后的直接结果，未添加增益.图7(b)整体信号强度更大是衰减补偿的效果.图7(b)与图7(a)相比，被衰减补偿的信号既有断层内部的错断面，也有背景的层面.对于断层下部的层面，电磁波在向下传播或者遇到界面向上反射的过程中，会经过断层高导高衰减区域，从而造成衰减.相应的，在逆时偏移的过程中，正传波场或者逆时反传波场在经过断层区域的时候就可以得到衰减补偿，恢复真实的振幅.

相比传统的探地雷达逆时偏移方法，衰减补偿逆时偏移方法不需增加额外的步骤和计算量.但在实际数据处理中需要注意噪声的影响.因为噪声也会在衰减补偿过程中被放大，特别是高频噪声.在强衰减的情况下，如果地面本身接收到的电磁信号已经被衰减到远低于噪声水平，噪声在逆时传播后期的衰减补偿过程中会被指数级放大.因而在处理实际数据时，必要的数据预处理是很有必要的，例如滤波处理等.对衰减补偿程度加以限制，防止过度补偿增强稳定性也是另外一个改进方向.

本文采用的衰减补偿逆时偏移方法理论上适用于任意复杂的电导率模型.但是在实际探地雷达数据处理中获取较为精确的电导率模型是主要的限制因素.前人已经在电法勘探中电阻率成像方法(Tripp et al., 1984; Sasaki 1994; Zhang et al., 1995; Auken et al., 2004)做了大量的工作，这些方法可被借鉴用于获取衰减补偿逆时偏移方法所需的电导率模型.井间探地雷达层析成像方法(Holliger et al., 2001; Chang et al., 2004; Giroux et al., 2007)与全波形反演方法(Ernst et al., 2007; Meles et al., 2010)也提供另外的获取精确电导率模型的方法.

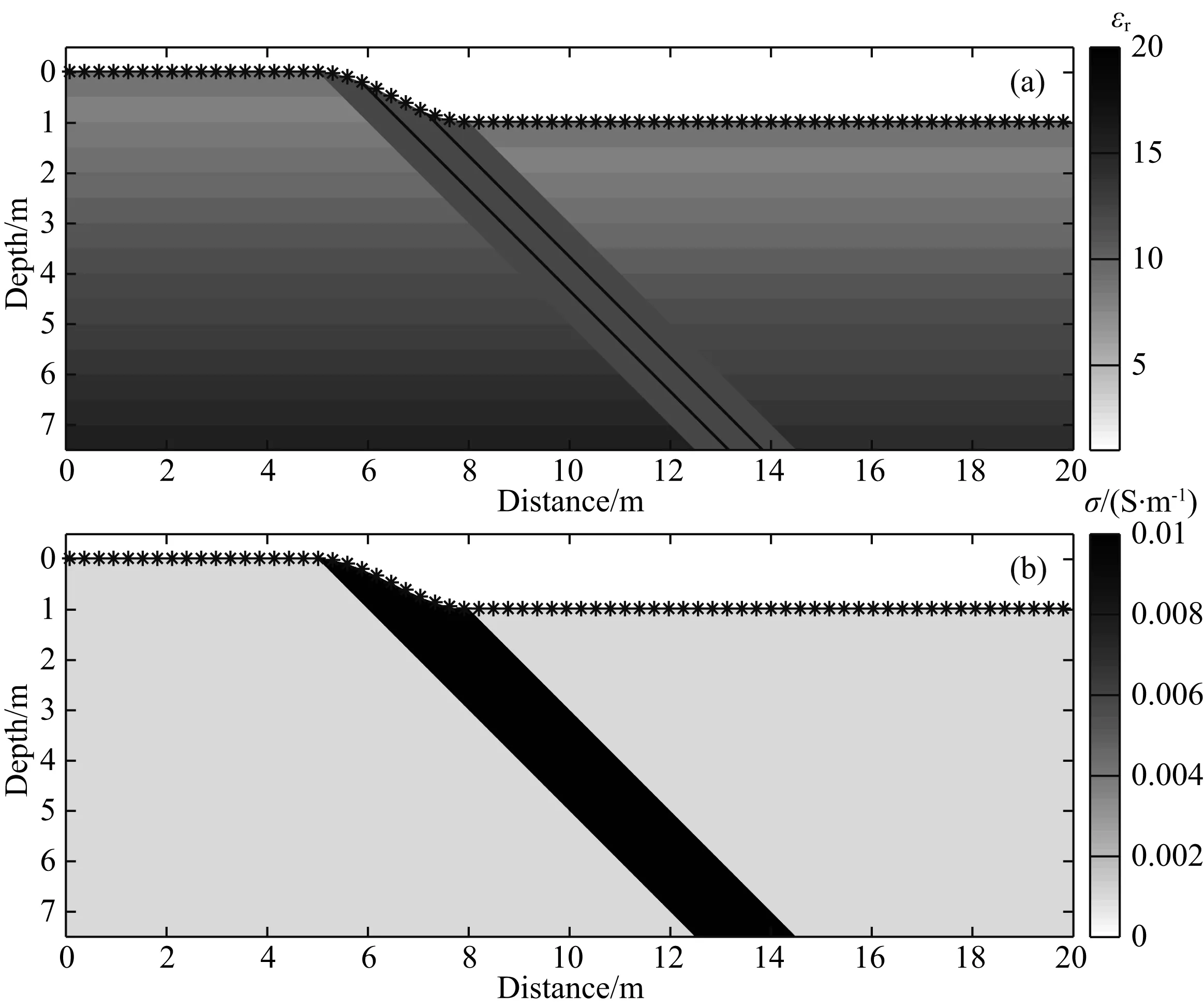
图5　渗水断层模型(a) 相对介电常数(εr)模型； (b) 电导率(σ)模型.模型模拟一个正断层，地面为陡坎形状，上部为空气层，中间高导区域(σ=0.01 S·m-1)为渗水后的断层破碎带.同时我们在相对介电常数模型中放置了两个高介电常数界面模拟内部的错断面.Fig.5　Fluid-infiltrated fault zone model(a) model of dielectric permittivity; (b) model of conductivity. This model has the shape of a normal fault with scarp. The top layer is air and the high conductive area (σ=0.01 S·m-1) corresponds to the fault-fracture zone which is permeated with water. Two interface of high dielectric permittivity are placed inside the fault-fracture zone to simulate fault-planes.

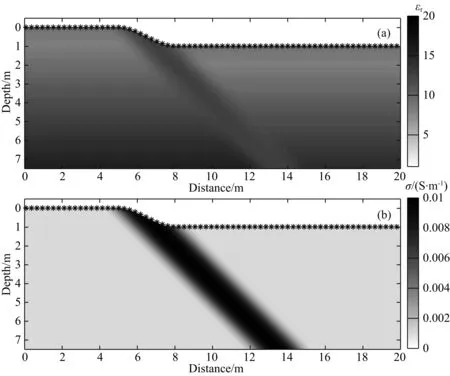
图6　用于逆时偏移的模型(a) 相对介电常数(εr)模型； (b) 电导率(σ)模型.该模型由图 5中模型经过高斯平滑后得到.Fig.6　Models for reverse time migration(a) model of dielectric permittivity; (b) model of conductivity. These models are generated by a Gaussian smoothing on the models in Fig.5.

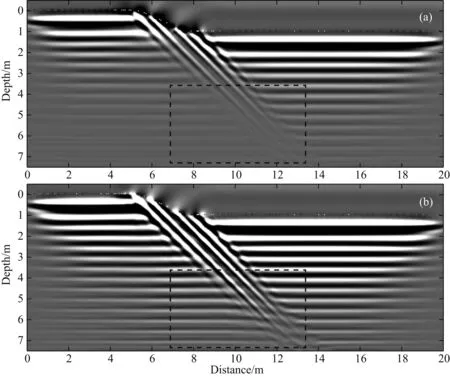
图7　渗水断层逆时偏移结果比较(a) 传统不考虑电导率逆时偏移结果； (b) 衰减补偿逆时偏移结果.Fig.7　Results of reverse time migration(a) Result of conventional reverse time migration; (b) Result of attenuation compensated reverse time migration.

4　结论

衰减补偿逆时偏移成像方法基于完整的电磁波方程，通过改变衰减项的正负号，保持了波动方程在逆时传播时的时间对称性，从而实现了对电导率造成的振幅衰减的补偿.通过与传统不考虑电导率影响的逆时偏移方法的比较，证明了衰减补偿逆时偏移成像能够很好地重构原始波场，恢复高衰减区域的信号强度，提高了成像的精度.

致谢感谢审稿专家和编辑部老师的支持和帮助.

Bradford J H. 2007. Frequency-dependent attenuation analysis of ground-penetrating radar data.Geophysics, 72(3):J7-J16.

Chang P Y, Alumbaugh D, Brainard J, et al. 2004. The application of ground penetrating radar attenuation tomography in a vadose zone infiltration experiment.JournalofContaminantHydrology, 71(1-4):67-87.Di Q Y, Xu K, Wang M Y. 2000. The attenuated radar wave migration with finite element method.ChineseJournalofGeophysics(in Chinese), 43(2):257-263.

Ernst J R, Maurer H, Green A G, et al. 2007. Full-Waveform Inversion of Crosshole Radar Data Based on 2-D Finite-Difference Time-Domain Solutions of Maxwell′s Equations.IEEETransactionsonGeoscienceandRemoteSensing, 45(9):2807-2828.

Etgen J, Gray S H, Zhang Y. 2009. An overview of depth imaging in exploration geophysics.Geophysics, 74(6):WCA5-WCA17.Fink M. 1992. Time reversal of ultrasonic fields. I. Basic principles. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 39(5):555-566.Fisher E, McMechan G A, Annan A P, et al. 1992. Examples of reverse-time migration of single-channel, ground-penetrating radar profiles.Geophysics, 57(4):577-586.

Giroux B, Gloaguen E, Chouteau M. 2007. bh_tomo—a Matlab borehole georadar 2D tomography package.Computers&Geosciences, 33(1):126-137.

Heteren S V, Fitzgerald D M, Mckinlay P A, et al. 1998. Radar facies of paraglacial barrier systems: coastal New England, USA.Sedimentology, 45(1):181-200.

Holliger K, Musil M, Maurer H R. 2001. Ray-based amplitude tomography for crosshole georadar data: a numerical assessment.JournalofAppliedGeophysics, 47(3):285-298.Irving J D, Knight R J. 2003. Removal of wavelet dispersion from ground-penetrating radar data.Geophysics, 68(3):960-970.

Kaelin B, Guitton A. 2006. Imaging condition for reverse time migration. In 2006 SEG Annual Meeting. Society of Exploration Geophysicists.Lei L L, Liu S X, Fu L, et al. 2015. Reverse time migration applied to GPR data based on full wave inversion.ChineseJournalofGeophysics(in Chinese), 58(9):3346-3355.

Leuschen C J, Plumb R G. 2001. A matched-filter-based reverse-time migration algorithm for ground-penetrating radar data.IEEETransactionsonGeoscienceandRemoteSensing, 39(5):929-936.

Liu S, Lei L, Fu L, et al. 2014. Application of pre-stack reverse time migration based on FWI velocity estimation to ground penetrating radar data.JournalofAppliedGeophysics, 107:1-7.

Meles G A, Van Der Kruk J, Greenhalgh S A, et al. 2010. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to- surface GPR data.IEEETransactionsonGeoscienceandRemoteSensing, 48(9):3391-3407.

Oden C P, Powers M H, Wright D L, et al. 2007. Improving GPR image resolution in lossy ground using dispersive migration.IEEETransactionsonGeoscienceandRemoteSensing, 45(8):2492-2499.

Radzevicius S. 2008. Practical 3-d migration and visualization for accurate imaging of complex geometries with gpr.JournalofEnvironmental&EngineeringGeophysics, 13(2):99-112.

Sasaki Y. 1994. 3-D resistivity inversion using the finite-element method.Geophysics, 59(12):1839-1848.

Sauck W A, Atekwana E A, Nash M S. 1998. High Conductivities Associated With an LNAPL Plume Imaged by Integrated Geophysical Techniques.JournalofEnvironmentalandEngineeringGeophysics, 2:203-212.

Sena A R, Stoffa P L, Sen M K. 2006. Split-step Fourier migration of GPR data in lossy media.Geophysics, 71(4):K77-K91.

Tripp A C, Hohmann G W, Swift C M. 1984. Two-dimensional resistivity inversion.Geophysics, 49(10):1708-1717.Turner G. 1994. Subsurface radar propagation deconvolution.Geophysics, 59(2):215-223.

Turner G, Siggins A F. 1994. Constant Q attenuation of subsurface radar pulses.Geophysics, 59(8):1192-1200.

Yoon K, Shin C, Suh S, et al. 2003. 3D reverse-time migration using the acoustic wave equation: An experience with the SEG/EAGE data set.TheLeadingEdge, 22(1):38-41.

Zhang J, Mackie R L, Madden T R. 1995. 3-D resistivity forward modeling and inversion using conjugate gradients.Geophysics, 60(5):1313-1325.

Zhang X W, Gao Y Z, Fang G Y. 2014. An inverse filtering method for removing the wavelet attenuation and dispersion of Ground Penetrating Radar data.ChineseJournalofGeophysics(in Chinese), 57(3):932-938.

Zhu T. 2014. Time-reverse modelling of acoustic wave propagation in attenuating media.GeophysicalJournalInternational, 197(1):483-494.

Zhu T, Harris J, Biondi B. 2014. Q-compensated reverse-time migration.Geophysics, 79(3):S77-S87.

附中文参考文献

底青云，许琨，王妙月. 2000. 衰减雷达波有限元偏移. 地球物理学报, 43(2):257-263.

雷林林，刘四新，傅磊等. 2015. 基于全波形反演的探地雷达数据逆时偏移成像. 地球物理学报, 58(9):3346-3355.

张先武，高云泽，方广有. 2014. 消除探地雷达数据的子波衰减和频散的反滤波方法. 地球物理学报, 57(3):932-938.

(本文编辑刘少华)

Attenuation compensated reverse time migration method of ground penetrating radar signals

ZHU Wei-Qiang, HUANG Qing-Hua*

DepartmentofGeophysics,SchoolofEarthandSpaceSciences,PekingUniversity,Beijing100871,China

Conductivity of subsurface media causes attenuation of ground penetrating radar (GPR) signals, so that the imaging results of conventional migration methods are blurred at strong attenuation zones. We proposed an attenuation compensated reverse time migration method for GPR signals. The forward and time-reverse propagation of electromagnetic waves was based on the Maxwell′s equations. The sign of the conductive term was reversed to keep equations′ temporal symmetry, so that the original wavefield could be reconstructed and the attenuation effect was compensated. The numerical experiments further compared the results of conventional reverse time migration and attenuation compensated reverse time migration. The imaging results showed that attenuation compensated method recovered the weak signals within and beneath high conductivity zones and improved the resolution of GPR profiles.

Ground penetrating radar; Attenuation compensation; Reverse time migration

Auken E, Christiansen A V. 2004. Layered and laterally constrained 2D inversion of resistivity data.Geophysics, 69(3):752-761.Bano M. 1996. Modeling and inverseQimaging of ground penetrating radar waves in 1 and 2D.GeophysicalResearchLetters, 23(22):3123-3126.Bitri A, Grandjean G. 1998. Frequency-wavenumber modelling and migration of 2D GPR data in moderately heterogeneous dispersive media.GeophysicalProspecting, 46(3):287-301.

10.6038/cjg20161034.

国家自然科学基金项目(41574104,41274075)资助.

朱尉强，男，1989年生，2013年毕业于北京大学，现北京大学地球物理专业研究生在读.

黄清华，男，教授，1990年毕业于中国科学技术大学，1999年获日本大阪大学博士学位.主要从事地球电磁学、地震物理学方面的教学和科研工作，E-mail：huangq@pku.edu.cn

10.6038/cjg20161034

P631

2015-12-21，2016-03-19收修定稿

朱尉强， 黄清华. 2016. 探地雷达衰减补偿逆时偏移成像方法. 地球物理学报，59(10):3909-3916,

Zhu W Q, Huang Q H. 2016. Attenuation compensated reverse time migration method of ground penetrating radar signals.ChineseJ.Geophys. (in Chinese),59(10):3909-3916,doi:10.6038/cjg20161034.