基于挤喷流效应的Russell流体因子推广及应用

张玉洁， 刘洪， 崔栋， 桂生， 冯玲丽

1 中国科学院地质与地球物理研究所，中国科学院油气资源研究重点实验室， 北京　100029 2 中国科学院大学， 北京　100049 3 中国石油勘探开发研究院， 北京　100083 4 中国石油新疆油田分公司勘探开发研究院， 新疆克拉玛依　834000



基于挤喷流效应的Russell流体因子推广及应用

张玉洁1,2， 刘洪1*， 崔栋3， 桂生1,2， 冯玲丽4

1 中国科学院地质与地球物理研究所，中国科学院油气资源研究重点实验室， 北京100029 2 中国科学院大学， 北京100049 3 中国石油勘探开发研究院， 北京100083 4 中国石油新疆油田分公司勘探开发研究院， 新疆克拉玛依834000

在油气勘探与开发过程中,寻求能够从地震资料中直接识别储层油气的流体指示因子至关重要.由于现存多数流体指示因子都是在Biot理论假设前提下建立起来的，因此在双相孔隙介质条件下不能有效地识别流体.为此，本文基于前人提出的双孔介质统一波动理论，考虑岩石裂缝间挤喷流效应，在经典流体指示因子基础上构建了一种新的流体指示因子.该流体因子能够较好地反映岩石内孔隙流体的变化对波传播产生的影响.在实际资料的应用中，采用多种方法分析、对比该流体识别因子与以Biot理论为基础的传统流体因子的优劣，理论分析与实际资料的验证表明该流体因子对于储层中油气的检测有较高的精度和灵敏度.

流体因子； 流体识别； 挤喷流效应； Biot-Gassmann理论

1　引言

流体因子实质上是一种用来表征地层含油气特征的地震属性，通常建立在岩石物理学基础上，与孔隙流体在地震资料中表现出的异常特性有关.而流体识别则是利用流体因子来识别储层内所含流体的类型，因此构建流体因子是识别油气藏流体类型的关键技术(印兴耀等. 2014).流体因子最早由Smith和Gidlow(1987)提出，并利用叠前数据计算了流体因子.随着进一步的研究，流体因子被赋予了更多样、更广泛的意义.Goodway等(1999)提出了λ-μ-ρ技术来识别储层流体，并将其作为流体因子.孔隙模量概念的提出，使得地震波纵横波阻抗成为流体识别的工具.Russel等(2003)基于Biot-Gassmann理论首先提出了用于描述流体性质的普适性方程，该方程比声波阻抗对饱和孔隙流体更加敏感.Smith和Gidlow(2003)依据叠前AVO分析，通过计算流体因子和交会图两种角度来识别孔隙中的流体.为了增大含流体介质的纵横波速区别，宁忠华等(2006)基于前人的方法对Russell流体因子进行改进，加入了纵横波阻抗的高阶项，构建了高灵敏度流体因子.Quakenbush等(2006)结合泊松比和密度属性提出了泊松阻抗的概念.王栋等(2009)则是利用纵横波阻抗多次幂的组合形式，使高次幂放大需要突出差异的地方，同时使低次量纲压制噪声.

以上方法都是基于Biot-Gassmann理论的孔隙结构假设.研究发现，基于Biot-Gassmann理论的流体因子对于固结成熟的碎屑岩储层孔隙流体具有较高的灵敏度.地下岩石介质含有大量的孔隙和裂隙，而这些孔隙和裂隙对于油气的赋存至关重要.孔隙与裂隙并存的情况下，裂隙的纵横比要比孔隙小很多，在外力的作用下，裂缝中的流体会被挤压到与其相连的孔隙中，产生挤喷流现象，因此描述岩石的弹性性质会相当复杂.Eshelby(1957)、Walsh(1965)等就针对裂隙对岩石弹性性质的影响进行了研究.在裂隙弹性力学方面，Budiansky和O′Connell(1976,1980)，O′Connell(1984)指出裂隙介质填充流体在外力作用下会产生“挤压喷流”现象.Biot理论及O′Connel和Budiansky的理论(这里简称OB理论)均不能完整地描述孔隙、裂隙并存时介质的弹性波动力学特征.为了寻求一个能够描述双相孔隙介质及对弹性波动影响的统一理论，White(1975)，Johnson(2001)以及Carcione等(2003)用孔隙流体的不均匀分布模拟了流体在裂隙、孔隙中的局部流动效应.Thomsen(1985)提出了一个使OB理论与Biot 理论相互兼容的理论，简称为Biot 相恰(Biot-Consistent)理论.Kuster和Toksöz(1974),Hudson(1981)探索了孔隙分布不均匀性对波传播造成的影响，并在弹性波的散射理论的基础上进行进一步的研究.Mavko和Nur(1979)用喷射流来描述流体在孔隙裂隙间局部流动产生的影响.Dvorkin和Nur(1993)在此基础上提出BISQ(Biot/squirt)理论，用来解释测量纵波时发现的高值频散现象.孔隙介质的研究中比较典型的一类是研究孔隙裂隙并存的介质，即双重孔隙介质理论和方法(Pride and Berryman, 2003; Berryman and Wang， 1995；Berryman，2006).巴晶(2010)也在Biot理论的基础上研究了弹性波在双相孔隙介质中的波动效应.Gurevich等(2010)将Biot理论连通孔隙介质条件推广到不连通或半连通，并构建了挤喷流频散和衰减的模型.

唐晓明(2011)对双孔之间的挤喷流效应进行了具体分析，并通过挤喷流效应与描述裂隙介质的重要参数之间的联系，得到了统一的波动理论，可以将孔隙与裂隙弹性波动力学结合起来.该理论不仅保持Biot理论基本特征及结构，还加入因裂隙造成的挤喷流项，提高了预测和模拟双孔介质中弹性波的精度，从而使得该理论的应用前景更为广泛.

本文以唐晓明提出的含挤喷流项的岩石物理方程为基础，对比Russell流体因子，推导出新的流体因子.

2　理论基础

本文所构造的流体因子是基于Biot-Gassmann理论的Russell流体因子构建与含孔隙、裂隙介质弹性波动的统一理论，因此首先介绍一下这两种理论.

2.1Biot-Gassmann理论

影响地震反射特性的主要因素是介质速度和密度，而介质含有孔隙并包含流体时，情况就变得复杂了.该问题首先被Biot(1941)提出，随后Gassmann(1951)也对该问题进行了研究，Kiref等(1990)指出Biot和Gassmann的结论是等价的.虽然之后又有很多理论被提出来，但是Biot-Gassmann理论是描述多孔介质纵横波速度稳定性最好、使用最广泛的理论.

Biot利用拉梅常数的关系得出:

(1)

其中λsat和λdry分别为饱和岩石与岩石骨架的第一拉梅常数，β为在孔隙内流体压力恒定的情况下流体与岩石体积变化之比，又称Biot系数，M为在确定岩石体积的情况下,流体挤入岩石骨架时所需的压力，是一个特定的模量.同理，Gassmann从K、μ、ρ出发,经推导得出以下的关系：

(2)

其中Ksat为饱和岩石的体积模量，Kdry为干燥岩石的体积模量.由(1)式和(2)式可得

(3)

μsat、μdry分别为饱和岩石和干燥岩石的剪切模量.这表明剪切模量是不受孔隙流体影响的.

在低频假设前提下，Gassmann指出：

(4)

(5)

其中，φ为孔隙度，Km、Kf分别为岩石骨架和流体的体积弹性模量.将β和M代入公式(2)可得Gaussman岩石物理方程具体的形式：

(6)

2.2含孔隙、裂隙介质弹性波动的统一理论

唐晓明在Gassmann的基础上提出新的岩石物理方程(公式(7))，该方程考虑了双孔介质的情况和弹性波动条件下裂隙之间流体的挤喷流效应，因此它可以有效地模拟与预测裂隙间流体的瞬间流动对波传播的影响. 不仅如此, 该方程还保持了Biot理论的基本特征及其结构.与Gassmann方程(6)相比，式(7)在分式的分母中多了一项表征挤喷流贡献的项S(ω).

(7)

(8)

(9)

其中f为频率变化因子，γ代表裂隙纵向尺度与横向尺度之比，η为流体的黏滞系数，ε为裂隙密度，Ks为基质的体积模量.J0是零阶贝塞尔函数，J1是一阶贝塞尔函数.ω是频率.式(8)中的K等效于式(7)中的K，这种情况下(8)式中关于K的表达式转变为隐函数关系，导致计算复杂化.在一级近似条件下，可以由不考虑“挤喷流”效应影响的(6)式计算得到(8)式中的K值，而μ的取值为式(3)中的干燥岩石剪切模量.类似的，υ可以是干燥介质的泊松比.需要说明的是，式(8)的计算结果主要由ε和γ二者共同控制的，它们是裂隙介质描述时最重要的参数.在实际资料的应用中这些参数可以由测井资料计算得到.

3　构建流体因子

Russell流体因子的构建过程是本文流体因子构建的基础，本文将从Russell流体因子的推导过程出发逐步推出新的流体因子.

均匀弹性无孔介质中纵横波速度的基本方程为：

(10)

这里保留用作区分干燥与饱和两种不同情况的β2M项，以强调其并不依赖方程(1)和(2)中等号左侧第一项.重新整理含饱和流体岩石的P波速度公式，在Biot理论框架下纵横波速度公式写为：

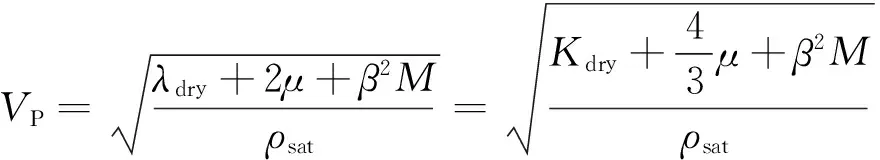
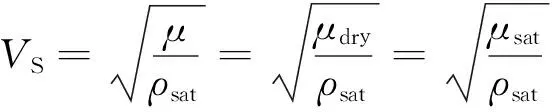
(11)

其中ρsat为岩石含有饱和流体时的密度.

由于这里考虑的流体为理想液体不存在切应力，对于饱和情况下的横波速度方程仅仅改变了密度项.因此这里仅对纵波速度进行讨论.

将公式(11)中受流体影响和不受流体影响的项分别用s和f表示，那么纵波速度表达式被重新写为

(12)

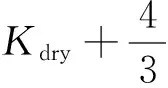
提取式(12)中的f并整理，得Russell流体因子表达式：

(13)

其中

(14)

ZS=ρVS,

(15)

(16)

Russell流体因子是基于Biot理论的流体因子，不考虑裂隙而仅考虑孔隙，且孔隙分布均匀，另外孔隙连通的假设也保证了波传播引起的孔隙流体流动是充分均衡的，即忽略了“挤喷流”效应对波传播的影响，使得弹性波传播经过裂隙时产生的相当可观的衰减和频散现象不能够得到更加准确地描述.为更加准确地描述孔隙、孔隙和裂缝并存的情况对弹性波传播的影响和含油气性，构造能更准确地指示流体赋存情况的流体因子，本文将唐晓明提出的挤喷流效应与流体因子结合进来.

将(7)式化为(2)式的形式可得

(17)

对比(11)式纵波速度可写为

(18)

此时

(19)

(20)

(21)

其中S(ω)为K的隐函数形式，可以对工区测井数据进行统计得到，而M可以用叠前反演方法所得到的纵横波速度与密度得到.将ρf作为新推导出的流体因子，记为NF.

该流体因子不仅保留了常规流体因子原有的特点及结构，还反映了挤喷流效应对波传播的影响.挤喷流项是由裂隙介质的两个最重要的参数，裂隙密度和纵横比所控制，因此挤喷流项能有效地体现裂缝对弹性波传播的影响.因此加入该项的新流体因子能够较好地模拟、预测介质含裂隙情况下弹性波在双孔介质中传播情况，提高流体预测的精度.新流体因子公式(20)中所需要的裂缝的密度及纵横比、纵波速度、横波速度与密度等参数均由测井资料与反演中得来.

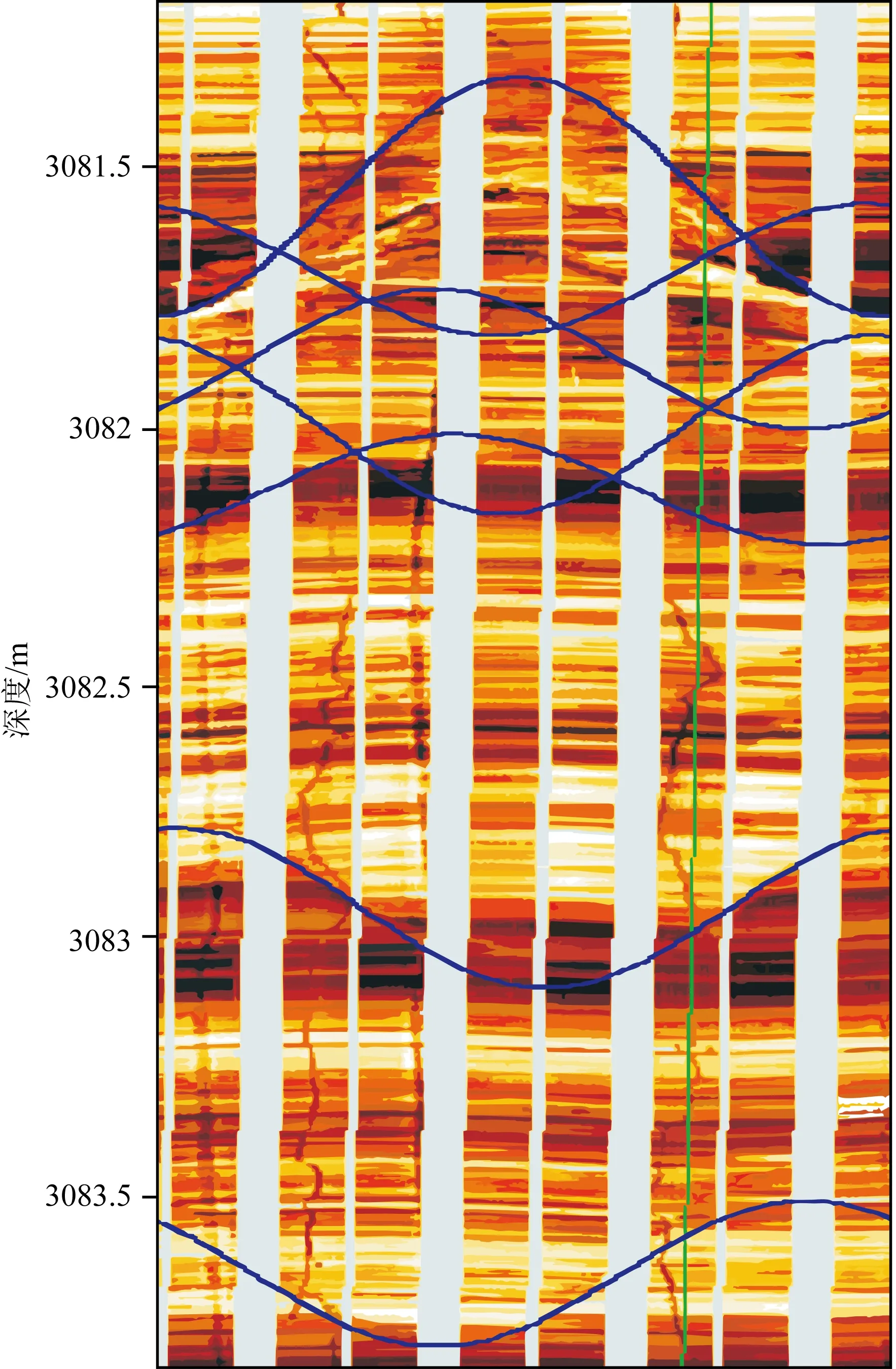
图1　基准井裂缝情况Fig.1　Fractures in stratigraphic well

4　数据试算

4.1储层岩石物理敏感参数分析

本文选取了某油田油页岩工区进行分析.主要岩性为泥岩、粉砂岩、油泥岩、泥质白云岩、泥质砂岩、白云岩、灰质泥岩、灰质油页岩、泥质灰岩、油页岩.目的层沉积环境为半深湖-深湖相.工区裂隙发育丰富(如图1).目标层地势西南高，东北低.在中部靠东北侧有一块高速体，已知为岩浆侵入体，且该岩浆侵入体区域内不含油气.储层岩石物理敏感参数分析选用所研究工区内有横波资料的井作为基准井，对其进行了多方面流体敏感度分析.

首先利用基准井各测井参数求出该井的NF，IF，泊松比，纵横波速比，HSFIF曲线(如图2).选取这些曲线上典型的含油段、含水段、干井段，然后再将这些流体指示因子的值与泊松比两两做成交会图进行比较.

图3为各流体因子与泊松比交会图，其中只有NF流体因子指示的参数与泊松比的交会图对含油层、干层和水层区分较为明显.我们还分析了Russell流体因子(这里简称FI流体因子)，该流体因子能够区分油层和水层，但无法区分油层和干层.纵横波速度比与泊松比的交会图、HSFIF流体因子与泊松比交会图都无法将油层区分出来.

图2　基准井流体因子Fig.2　Fluid factors of stratigraphic well

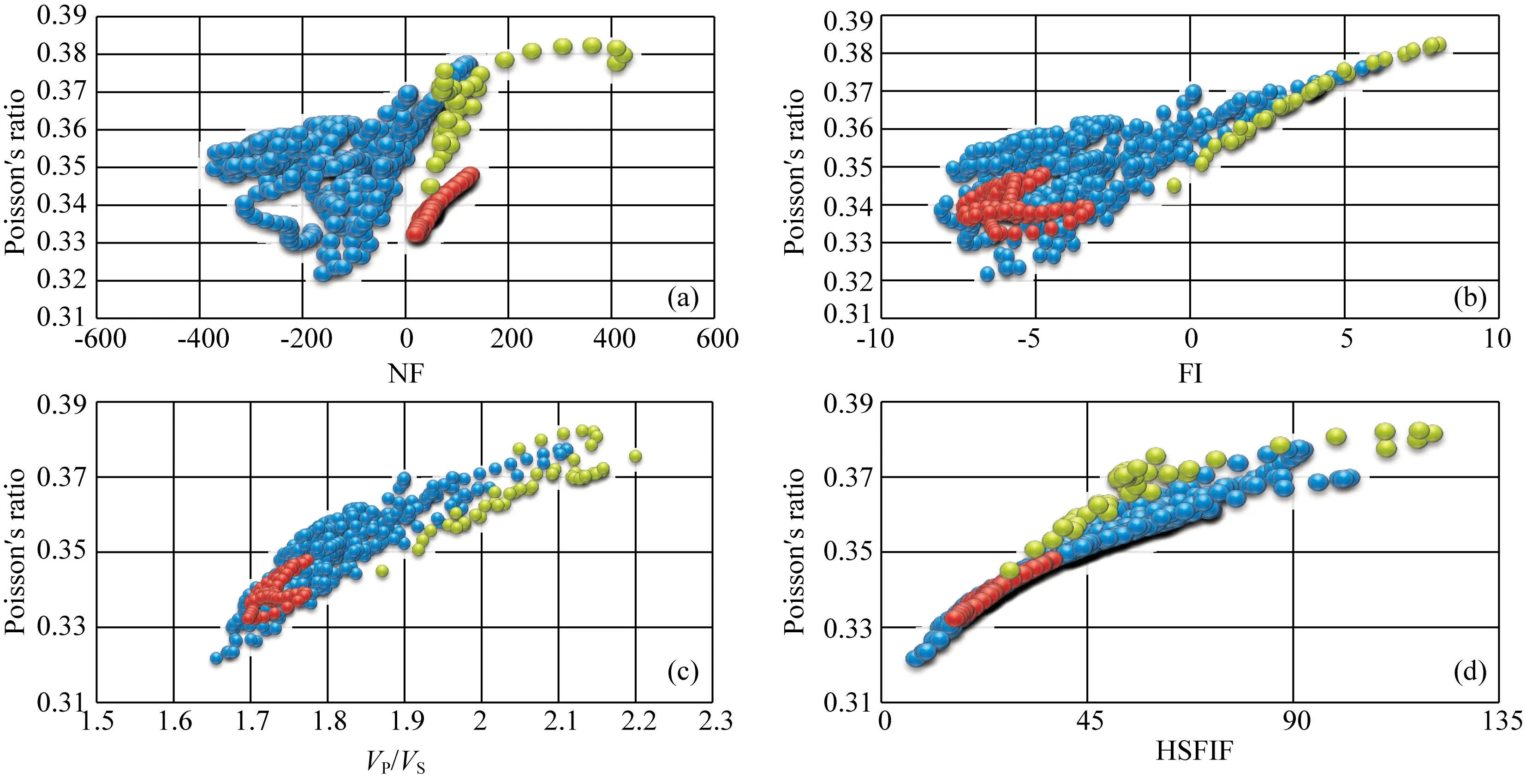
图3　岩石物理参数分析交会图蓝色为油层，红色为干层，黄色为含水层. Fig.3　Cross plots of rock physical parameters Blue points represents oil, red points represents dry rock, yellow points represents water.

本文计算了该区有背景岩性影响情况和无背景岩性影响情况下多个流体因子的流体指示系数，并对结果进行综合分析.无背景岩性影响(Dillon, 2003)情况下(如图4)，Russell流体因子f，泊松比，VP/VS的流体指示系数较高.再结合交会图(图3)，以上流体因子可以在目标区域将油水区分开，但是却不能将含油储层与背景岩层明确区分.

有背景岩性影响情况下(如图5)NF，泊松比，HSFIF流体指示系数较高，再与交会图进行综合分析，可以将油与水和背景岩层区分开.因此，NF流体因子受工区背景岩性影响较小，对本工区流体的指示有着较好的效果.

4.2有利储层分析及油气预测

图6为目标层构造图.该区为油页岩区块，断层裂隙发育.在图7的NF流体因子预测中可以看到含油范围与井产油情况基本吻合.从储层叠前属性切片(图7)上分析，NF值较低的位置为良好的油气储层位置，与实际钻井产油情况基本吻合，黄色区域的分布范围基本包含了所有的产油井，干井基本都在蓝色区域内.这验证了NF流体因子的有效性，与产油井情况的吻合度为85.7%.对比泊松比切片(图8)和HSFIF流体因子切片(图9)，泊松比切片受地势构造影响严重.西南方向高地势位置流体指示过多，而东北部低地势位置流体指示过少.HSFIF流体因子受背景岩性影响严重，在岩浆侵入体位置有错误的油气指示.

图4　无背景岩性影响情况下的流体指示系数Fig.4　Coefficient of fluid indicator without background lithology influence

图5　有背景岩性影响情况下的流体指示系数Fig.5　Coefficient of fluid indicator with background lithology influence

图6　目标层构造图Fig.6　Structure of target layer

图7　NF流体因子目标沿层切片Fig.7　NF slice of target layer

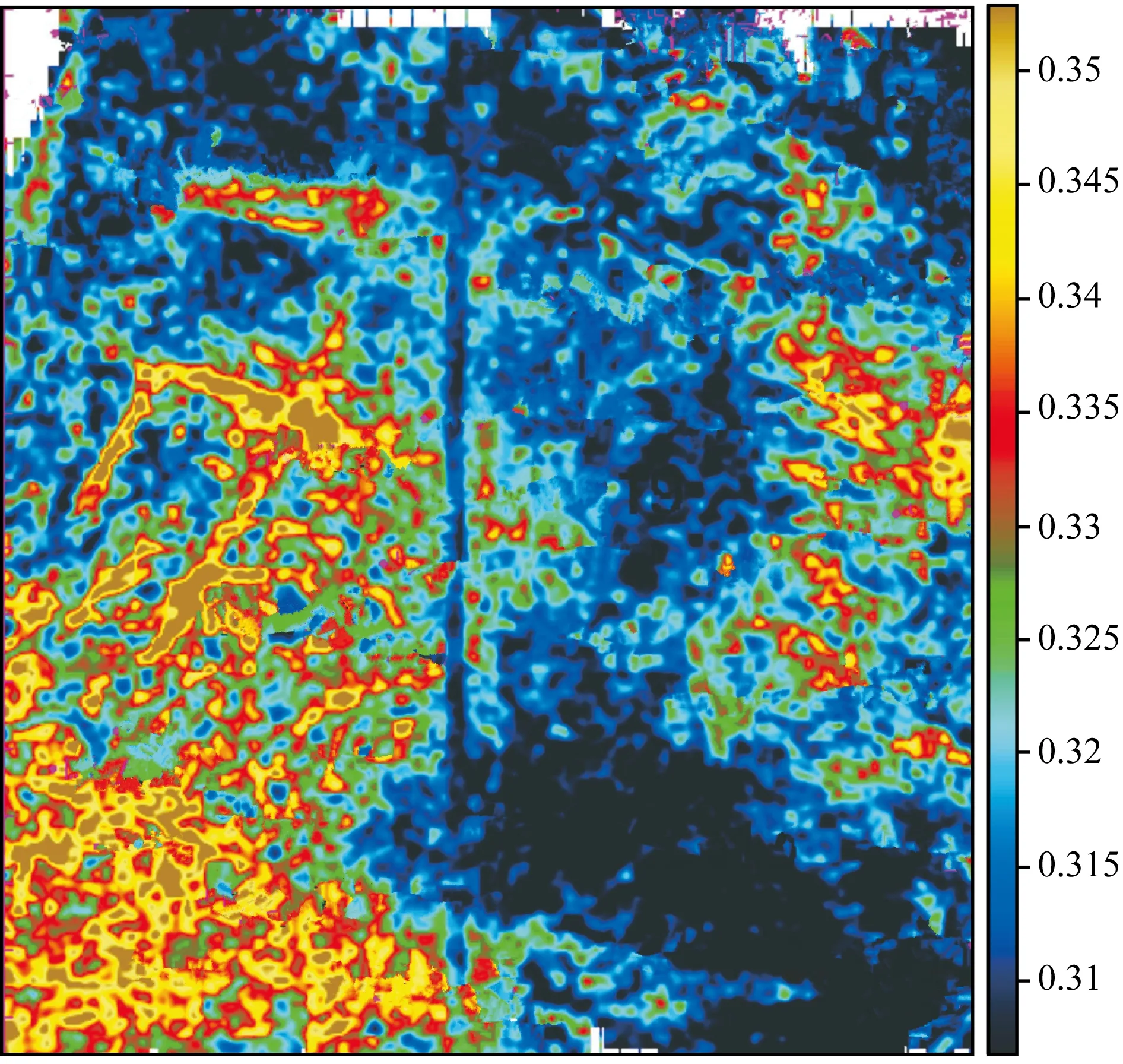
图8　泊松比目标沿层切片Fig.8　Poisson ratio slice of target layer

图9　HSFIF流体因子目标沿层切片Fig.9　HSFIF slice of target layer

将构造图(图6)覆盖于流体因子切片之上，也可以看到断裂发育的部位同时发育良好储层.说明反演结果不但能够反映储层地球物理特征，还对工区内的构造特征进行了一定程度的反映.

5　结论与认识

流体因子能够较好地指示储层流体的分布情况，对于储层的预测起着至关重要的作用.通过反演得到的速度密度信息，可以方便地计算多种流体因子.本文结合挤喷流效应对流体指示的影响，提出了一种新的流体指示因子，即NF流体因子.交会分析表明NF流体因子对裂缝、裂隙油气储集体中油气指示效果良好.实际工区内含油气范围也表明该流体因子对于储层的展布情况有较为准确的预测.通过理论分析和实际资料验证，NF流体因子能够对页岩裂缝发育区域的流体进行较准确的预测，有较好的应用前景，为裂缝发育的泥页岩探区的勘探开发提供可靠的依据.

Ba J. 2010. Wave propagation theory in double-porosity medium and experimental analysis on seismic responses.ScientiaSinica(Physica,Mechanica&Astronomica) (in Chinese), 40(11): 1398-1409.

Berryman J G, Wang H F. 1995. The elastic coefficients of double-porosity models for fluid transport in jointed rock.JournalofGeophysicalResearch:SolidEarth(1978—2012), 100(B12): 24611-24627.

Berryman J G. 2006. Effective medium theories for multicomponent poroelastic composites.JournalofEngineeringMechanics, 132(5): 519-531.

Biot M A. 1941. General theory of three-dimensional consolidation.JournalofAppliedPhysics, 12(2): 155-164.

Budiansky B, O′Connell R J. 1976. Elastic moduli of a cracked solid.InternationalJournalofSolidsandStructures, 12(2): 81-97.

Budiansky B, O′Connell R. 1980. Bulk dissipation in heterogeneous media.SolidEarthGeophysicsandGeotechnology, 42: 1-10.

Carcione J M, Helle H B, Pham N H. 2003. White's model for wave propagation in partially saturated rocks: Comparison with poroelastic numerical experiments.Geophysics, 68(4): 1389-1398. Dillon L, Schwedersky G, Vásquez G, et al. 2003. A multiscale DHI elastic attributes evaluation.TheLeadingEdge, 22(10): 1024-1029.

Dvorkin J, Nur A. 1993. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms.Geophysics, 58(4): 524-533.

Eshelby J D. 1957. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the Royal Society of London.SeriesA:MathematicalandPhysicalSciences, 241(1226): 376-396.

Gassmann F. 1951. Elastic waves through a packing of spheres.Geophysics, 16(4): 673-685.

Goodway B, Chen T W, Downton J. 1999. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters; “λρ”, “μρ”, & “λ/μfluid stack”, from P and S inversions.∥ 1997 SEG Annual Meeting. Dallas, Texas: SEG.

Gurevich B, Makarynska D, de Paula O B, et al. 2010. A simple model for squirt-flow dispersion and attenuation in fluid-saturated granular rocks.Geophysics, 75(6): N109-N120.

Hudson J A. 1981. Wave speeds and attenuation of elastic waves in material containing cracks.GeophysicalJournalInternational, 64(1): 133-150.

Johnson D L. 2001. Theory of frequency dependent acoustics in patchy-saturated porous media.TheJournaloftheAcousticalSocietyofAmerica, 110(2): 682-694.

Krief M, Garat J, Stellingwerff, et al. 1990. A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic).LogAnalyst, 31: 355-369.

Kuster G T, Toksöz M N. 1974. Velocity and attenuation of seismic waves in two-phase media: Part I. Theoretical formulations.Geophysics, 39(5): 587-606. Mavko G M, Nur A. 1979. Wave attenuation in partially saturated rocks.Geophysics, 44(2): 161-178.

Ning Z H, He Z H, Huang D J. 2006. High sensitive fluid identification based on seismic data.GeophysicalProspectingforPetroleum(in Chinese), 45(3): 239-241.

O′Connell R J. 1984. A viscoelastic model of anelasticity of fluid saturated porous rocks.∥ Physics and Chemistry of Porous Media. Schlumberger: AIP Publishing, 166-175.

Pride S R, Berryman J G. 2003. Linear dynamics of double-porosity dual-permeability materials. I. Governing equations and acoustic attenuation.PhysicalReviewE, 68(3): 036603.

Quakenbush M, Shang B, Tuttle C. 2006. Poisson impedance.TheLeadingEdge, 25(2): 128-138.

Russell B H, Hedlin K, Hilterman F J, et al. 2003. Fluid-property discrimination with AVO: A Biot-Gassmann perspective.Geophysics, 68(1): 29-39. Smith G C, Gidlow P M. 1987. Weighted stacking for rock property estimation and detection of GAS.GeophysicalProspecting, 35(9): 993-1014.

Smith G C, Gidlow M. 2003. The fluid factor angle and the crossplot angle. ∥ 2003 SEG Annual Meeting. Dallas, Texas: SEG, 185-188.

Tang X M. 2011. A unified theory for elastic wave propagation through porous media containing cracks—An extension of Biot′s poroelastic wave theory.ScientiaSinica(EarthScience) (in Chinese), 41(6): 784-795.

Thomsen L. 1985. Biot-consistent elastic moduli of porous rocks: Low-frequency limit.Geophysics, 50(12): 2797-2807

Walsh J B. 1965. The effect of cracks on the compressibility of rock.JournalofGeophysicalResearch, 70(2): 381-389.

Wang D, He Z H, Huang D J. 2009. Construction of a new fluid identification factor and analysis on its application.GeophysicalProspectingforPetroleum(in Chinese), 48(2): 141-145.

White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation.Geophysics, 40(2): 224-232.

Yin X Y, Cao D P, Wang B L, et al. 2014. Research progress of fluid discrimination with prestack seismic inversion.OilGeophysicalProspecting(in Chinese), 49(1): 22-34.

附中文参考文献

巴晶. 2010. 双重孔隙介质波传播理论与地震响应实验分析. 中国科学: 物理学 力学 天文学, 40(11): 1398-1409.

宁忠华, 贺振华, 黄德济. 2006. 基于地震资料的高灵敏度流体识别因子. 石油物探, 45(3): 239-241.

唐晓明. 2011. 含孔隙、裂隙介质弹性波动的统一理论——Biot理论的推广. 中国科学: 地球科学, 41(6): 784-795.

王栋, 贺振华, 黄德济. 2009. 新流体识别因子的构建与应用分析. 石油物探, 48(2): 141-145.

印兴耀, 曹丹平, 王保丽等. 2014. 基于叠前地震反演的流体识别方法研究进展. 石油地球物理勘探, 49(1): 22-34.

(本文编辑何燕)

Construction and application of the Russell fluid factor with squirt flow effect

ZHANG Yu-Jie1,2， LIU Hong1*， CUI Dong3, GUI Sheng1,2, FENG Ling-Li4

1KeyLaboratoryofPetroleumResourcesResearch,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China2UniversityofChineseAcademyofSciences,Beijing100049,China3ResearchInstituteofPetroleumExplorationandDevelopment,CNPC,Beijing100083,China4InstituteofExplorationandDevelopment,XinjiangOilfieldCompany,CNPC,XinjiangKaramay834000,China

In the exploration process of oil and gas, it is important that using a fluid factor to identify gas and oil from seismic data directly. In this work, on the basis of the classical fluid indication factor analysis, we built a new indication factor named as NF fluid factor. Adding the squirt fluid effect between the cracks of rocks, the fluid factor indicates the fluid in the rock pore more possible. It plays a vital role in predicting reservoirs. We compared it with other fluid factors through many methods. We found that it not only indicates the oil but also indicates the dispersion of fractures without the influence of lithology. In oil shale reservoirs, fractures are the main accumulate space, which means that it is the fracture where oil is present. We also compared the production of wells with NF fluid factor time slice and found that the percent of consistence is 85%. In conclusion, the NF fluid factor can indicate the oil from oil shale and ignore the influence of lithology. It is a perfect fluid factor to predict oil in shale. It has been used in real exploration and works well.

Fluid factor; Fluid identification; Squirt flow effect; Biot-Gassmann theory

10.6038/cjg20161033.

中石油新技术新方法项目“GPU/CPU加速弹性介质全波形反演研究”、中国石油天然气集团公司科学研究与技术开发项目“弹性波地震成像技术合作研发与应用”，国家高技术研究发展计划(863计划)(2012AA061202)，国家重大专项(2016ZX05003003)联合资助.作者简介张玉洁，女，1988年生，博士研究生，主要从事地震波成像和油储地球物理研究. E-mail: zhangyujie@mail.iggcas.ac.cn

刘洪，男，1959年生，研究员，主要从事地震波成像和油储地球物理研究. E-mail: liuhong@mail.iggcas.ac.cn

10.6038/cjg20161033

P631

2015-08-02，2015-12-31收修定稿

张玉洁，刘洪，崔栋等. 2016. 基于挤喷流效应的Russell流体因子推广及应用. 地球物理学报，59(10):3901-3908,

Zhang Y J， Liu H， Cui D,et al. 2016. Construction and application of the Russell fluid factor with squirt flow effect.ChineseJ.Geophys. (in Chinese),59(10):3901-3908,doi:10.6038/cjg20161033.