一种改进的图像无缝拼接算法
2016-11-08陈淑清
陈淑清
(1.莆田学院信息工程学院,福建莆田351100;2.福建省大数据管理新技术与知识工程重点实验室&智能计算与信息处理福建省高等学校重点实验室,福建泉州362000)
一种改进的图像无缝拼接算法
陈淑清1,2
(1.莆田学院信息工程学院,福建莆田351100;2.福建省大数据管理新技术与知识工程重点实验室&智能计算与信息处理福建省高等学校重点实验室,福建泉州362000)
针对图像拼接过程产生的接缝问题,采用最佳接缝选择算法缝合图像接缝。然而合适的能量函数是最佳接缝选择算法的关键。提出一种基于Canny边缘检测算子改进的能量函数,其目的是最小化图像重叠区域的梯度差异。通过实验将提出的能量函数与亮度误差、梯度差、梯度和、梯度差和梯度和的加权和以及Canny边缘检测算子等五种常用能量函数的最佳接缝选择结果进行对比。结果表明,提出的能量函数可以减少拼接图像的结构接缝,而且对于光照变化具有更好的分割稳定性,使得拼接之后的图像看起来更加自然美观。
无缝拼接;Canny边缘检测算子;多分辨率融合
图像拼接是图像处理领域的主要研究课题之一,近年来国内外专家学者在这个领域做了大量的研究工作。图像拼接的两个关键步骤是图像配准和接缝消除[1]。拼接图像的接缝包括纹理结构不一致引起的结构接缝和亮度不一致引起的光学接缝。针对这两种接缝,最常用的接缝消除算法分别是最佳接缝选择算法和接缝平滑算法。目前一些主流的最佳接缝选择算法在不同程度上都会割裂纹理结构,造成比较明显的结构接缝。本文着重讨论最佳接缝选择算法,本着使待拼接图像重叠区域内、接缝周围图像纹理差异最小的指导思想,提出了基于Canny边缘算子改进的最佳接缝选择算法。对于存在亮度差异的图像,在选择了最佳接缝的基础上应用多分辨率融合算法,使图像之间平滑过渡,同时又能使得图像依然保持清晰的纹理。实验表明,文章提出的方法与其它五种的接缝优化算法相比,能够更好地保持拼接图像纹理结构的一致性。
1 主要最佳接缝选择算法
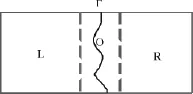
图1 部分重叠图像示意图
如图1所示。在已经配准的两幅部分重叠的图像和的重叠区域Ω内,求解一条符合某种约束条件的缝合接缝。最佳接缝选择算法涉及两个关键步骤,一是约束条件,二是求解满足约束条件的分割算法。常见求解最佳接缝的算法有动态规划算法和图割算法。接下来以垂直接缝为例来叙述。
约束条件往往是沿着接缝线上的所有像素点的能量之和达极小值。不同的能量函数构成了不同的约束条件。能量函数有直接基于图像像素灰度值的,也有基于图像梯度域的。令和分别为沿着垂直接缝线上的两个重叠块,如图2所示。常见的能量函数主要有以下几种。
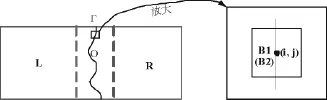
图2 接缝约束条件
(1)最小化接缝上重叠像素的亮度误差,对于RGB图像,可以分别计算每个通道的亮度差,再取三通道误差的和。能量函数如下:

公式(1)中E1表示单组重叠块的亮度误差,I1和I2分别表示重叠块B1和B2的上各点的像素值,B表示重叠块区域;
(2)最小化重叠区域梯度和。能量函数如下:

(3)最小化重叠区域梯度差。能量函数如下:

其中表示梯度运算。
(4)最小化E2和E3的加权和[2]。能量函数如下:

其中β=0.7。
对于以上四种主要的能量函数,设Γ为最佳接缝线,求解最佳接缝的约束条件是沿着接缝所有重叠块能量之和达最小值。即,

2 提出的方法
两幅经过配准、存在重叠区域的待拼接图像之间可能存在亮差、色差,也可能存在一些几何结构上的错位。直接加权融合这样的图像往往会引起图像在亮度或色彩上的过渡不自然而留下的光学接缝以及由于几何结构错位引起的重影、鬼影或者图像模糊等现象。在实验分析的过程中发现,常见的最佳接缝的算法常常会切断一些几何结构的边缘,结构错位容易呈现出来。想要合成一幅在几何结构上无明显错位的图像,接缝应该使周围图像重叠区域的边缘或纹理尽量一致。文章提出采用基于Canny边缘检测算子改进的最佳接缝选择算法。对于存在明显亮度差异的图像,可以在选择好最佳接缝之后,对图像的重叠区域应用基于最佳接缝掩膜的多分辨率融合,平滑接缝周围的亮度差异。
2.1Canny边缘检测算子
Canny边缘检算子[3]是Canny于1986年提出来的一种双阈值边缘检测算子。边缘体现在二维图像信号上即为亮度的阶跃变化,常常用图像的梯度来度量边缘的强度。边缘检测的过程本质上就是对图像梯度进行检测、度量和定位的过程。Canny检测算子的步骤:(1)平滑图像,抑制噪声;(2)检测图像梯度的幅值和方向;(3)对梯度的幅值应用非极大值抑制;(4)用双阈值算法检测和连接边缘。
2.2基于Canny改进的能量函数
基于Canny的能量函数,最小化Canny边缘差异:

其中C1和C2分别是重叠块内两幅图像的Canny二值边缘响应。
在Canny边缘算子的基础上,提出新的能量函数,它是基于图像的梯度幅值的。该能量图像E(x,y)的计算方法如公式(7)和(8)所示。

其中NC为论文提出的基于Canny边缘算子的一种新的边缘度量方法,M(x,y)是Canny算子中梯度幅值,其计算方法和Canny算子[3]一样,th1和th2分别为Canny边缘算子中的高、低两个阈值,e(x,y)=1表示当前像素属于Canny边缘点,e(x,y)=0表示当前像素不属于Canny边缘点。对于彩色图像,文章采用的方法是计算R、G、B三通道的能量图像之和,见公式(9);也可以先将彩色图转换成灰度图像再计算能量图像。
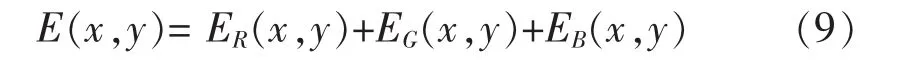
结合Canny的双阈值边缘检测算子,使算法具有更好的鲁棒性。这里的边缘度量方式是基于图像的梯度幅值,对于图像亮度的加性变化具有不变性,但图像的乘性变化会使图像梯度幅值发生相应的改变。为了让梯度幅值对图像的亮度具有仿射不变性,在计算过程中对图像的梯度幅值进行了规范化处理。
2.3最佳接缝选择算法
最佳接缝选择算法的目标是在图像的重叠区域内找到一条缝合线,使得沿着缝合线的所有像素的能量之和最小。本文采用动态规划算法来求解最佳缝合线[4]。以垂直方向的缝合线为例,如图3所示。对于缝合线上的每个点,它的邻接点只能为左上方、正上方和右上方三个点。垂直方向的缝合线,不考虑其水平邻接点。则动态规划算法的递归式如公式(10)所示。

图3 动态规划

Eij表示累计误差,(i,j)为缝合线Γ上的一点,min为取最小值操作。选择当(i,j)落在图像的底部时,累计误差最小的轨迹即为最佳接缝。对于大小为m×n的图像重叠区域,自上而下计算接缝线上的能量之和S(i,j),其中第一行等于E(i,j),之后的每一行的计算方法见公式(10)。最后一行S(m,j)的值即为n个当前最小能量之和。取S(i,j)最后一行S(m,j)中的最小值即为最佳缝合线上的能量之和。沿着这个最小值往前回溯,找出最佳缝合线。
2.4基于最佳接缝掩膜的多分辨率融合
文章提出的方法重点在于处理结构上的差异,但是没有考虑两幅图像的亮度差异,需要应用接缝平滑算法来使重叠区域在亮度上能够平滑过渡。对于存在明显亮度差异的两幅图像,可以先应用文章提出的最佳接缝算法分割重叠区域,再应用多分辨率融合算法以平滑重叠区域亮度的差异。即,将最佳分割应用于融合掩模R,置分割左边的R值为1,分割线右边的R值为0。
多分辨融合的思想是Burt和Adelson[5]提出来的。它首先将待融合的图像分解成不同频带的子图,然后对不同的频带沿着分割边界应用不同的融合半径,对于像图像亮度等大尺度特征,分布在低频带,采用大的融合半径,使图像在重叠区域过度自然,对于纹理等细节特征,分布在高频带,采用小的融合半径,以免图像模糊或重影。通过这种多分辨率融合算法巧妙地把分割算法和融合算法整合在一起。
多分辨率融合算法首先需要对原图像进行多分辨率分解,构建多分辨率金字塔,这一步有不同的算法可以应用,如拉普拉斯、小波分解、离散傅里叶变换等。这里以构建拉普拉斯金字塔为例阐述多分辨融合的一般步骤如下:
(1)分别构建图像A和B的拉普拉期金字塔LA和LB;
(2)构建融合掩模R的高斯金字塔GR;
(3)以高斯金字塔GR上对应结点为融合权值构建拉普拉斯金字塔LA和LB的融合金字塔LC:
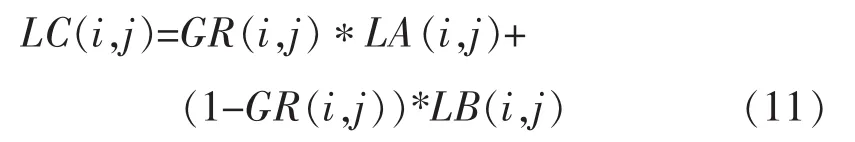
(4)由拉普拉斯金字塔LC重构最终的融合图像C。
3 实验及结果分析
3.1算法相关参数设置
最佳接缝选择过程中,计算能量图像的时候,首先需要考虑的是计算接缝线上每个像素的能量所采用的重叠块B的大小。如图4所示,通过实验比较了6-领域块和2-邻域块这两种不同重叠块大小对分割结果的影响。图中的黑点表示像素点,用红色的圆圈出来的点表示当前需要计算能量的像素。通过仿真实验分别比较了这两种块大小在不同能量函数情况下的分割效果。实验结果表明,总体上2-领域块优于6-领域块,且能量函数的1范数和2范数的表现差别不大。因此在后续的实验中,所有的能量函数图像均采用2-领域块和1范数,即绝对值来计算。

图4 能量图像中重叠块B的选择
最后,探讨Canny边缘算子阈值的选择。这个阈值是基于梯度幅值的,由于图像的对比度各不相同,选择的一个确定的阈值是很困难的。这里采用相对阈值的方法,假设一幅图像中有一定百分比的像素点为非边缘点。这里取70%,把比70%的像素点的梯度幅值高的幅值确定为高阈值th1,并令th2=0.4th1。
3.2仿真实验
本实验采用的一组仿真图像均截取自同一张图像,大小为512×512,左图和右图在垂直方向存在8个像素的错位,并对右图加上1.1的乘性亮度变化和20的加性亮度变化,生成新的右图。这组图像存在圆弧形边缘,比较全面的包含了各种不同的边缘方向,图像中不均匀的亮度包括了各种不同的边缘强度,是一组比较有代表性的仿真图像。采用直接取中线作为垂直接缝的拼接结果如图5所示。两幅图像均存在明显的结构接缝,图5(b)还存在亮度差异。两幅图像在视觉上明显失真,看起来不自然。

图5 取中线作为垂直接缝直接拼接的图像
3.2.1最佳接缝选择

图6 对无亮差图像应用最佳接缝选择

图7 对存在亮度差异图像应用最佳接缝选择
先后比较了本文提出的能量函数、四种常用能量函数及基于Canny边缘算子差的能量函数在图像没有亮度差异和有亮度差异两种情况下的接缝选择的结果。对于梯度域的能量函数,在计算能量函数之前都对图像的梯度做了规范化。实验结果如图6和图7所示。本实验使用离中线左右各60像素的区域作为接缝的候选区域。
分析图6可以看出,图(b)、(c)和(d)在中间自上而上第一朵小白花或第二朵小白花左边的弧形轮廓上存在多处比较明显的裂痕;图(e)在第一朵小花左上方轮廓线上存在一处比较明显的毛边;图(a)与论文提出的方法最接近,在第一朵小花的左上方存在一处与图(f)相似的细微接缝,但是它在第二朵小花左上方轮廓线上存在一处比较明显的结构接缝。图(f)只是在第一朵小白花左上方的轮廓上存在一点点细微的结构接缝,肉眼看起来并不明显,整体效果比其它五种能量函数的拼接结果都要好一些。
分析图7可以看出,同样是论文提出的算法获得了比较好的拼接结果。图(f)除了在亮度上存在差异之外,在结构缝合上接近完美,肉眼上看不出结构接缝。此外,基于梯度域的E2、E3和E4整体表现与图6并无明显上的差异,符合预期。E1能量函数应用在存在亮度差异图像上分割结果有了比较明显的变化,简单的亮度差异最小化不适合用于存在亮度差异图像的拼接。Canny边缘算子差的能量函数E5也因图像亮度的变化导致求解的分割线产生了不小的波动。相比之下,文章提出的能量函数E产生的分割比较稳定,没有因为亮度差异而产生明显的变化。
3.2.2接缝平滑

图8 对图7(f)应用多分辨率融合
如图7(f)所示,正如预期,拼接图像中间存在比较明显的亮度差异。对拼接图像中间120像素宽的重叠区域应用多分辨率融合算法,其结果如图8所示。经过基于最佳接缝掩膜的多分辨率融合之后的拼接图像处理的结果图像没有明显的结构接缝,也在一定程序上抑制了光学接缝,整幅图像亮度过度自然。
4 小结
本文着重探讨结构接缝的消除或最小化,提出了一种用于最佳接缝选择的能量函数。这种能量函数是基于Canny边缘算子改进而来的,它是基于图像的梯度幅值的。对于存在亮度差异的图像,可以在最佳分割的基础上应用基于最佳接缝掩膜的多分辨率融合算法,平滑接缝。实验表明,与原来的直接基于Canny边缘响应差的能量函数或其它四种常用的能量函数相比,本文提出的能量函数具有较好的分割效果,且能适应图像亮度变化,具有更好的分割稳定性。在最佳分割的基础上再应用多分辨率融合,能够兼顾纹理结构一致和亮度的平滑,取得较好的效果。
[1]李海超,郝胜勇,朱琦.多片遥感图像的快速无缝拼接方法[J].经外与激光工程,2011,40(7):1381-1386.
[2]Jiaya J,Chi-Keung T.Image stitching using structure deformation[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2008,30(4):617-631.
[3]Canny J.A computational approach to edge detection[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,1986(6):679-698.
[4]Avidan S,Shamir A.Seam carving for content-aware image resizing[C].ACM Transactions on graphics(TOG).ACM,2007,26(3):10.
[5]Burt P J,Adelson E H.A multi-resolution spline with application to image mosaics[J].ACM Transactions on Graphics(TOG),1983,2(4):217-236.
(责任编辑:华伟平)
An Improved Algorithm for Seamless Image Stitching
CHEN Shuqing1,2
(1.College of Information Engineering,Putian University,Putian,Fujian 351100;2.Fujian Provincial Key Laboratory of Data Intensive Computing&Key Laboratory of Intelligent Computing and Information Processing,Fujian Province University,Quanzhou,Fujian 362000)
Concerned the seams problem arising from image stitching,an optimal seam selection algorithm is used.And an appropriate energy function is the key to the algorithm.An improved energy function based on Canny detector is proposed in this paper.Its goal is to minimize the differences of the gradients between overlapped areas of the images.Moreover,the proposed energy function is compared with the other five common ones by experiments,which include the brightness errors,the gradient errors,the gradient sums,the weighted sum of the gradient errors and sums,and Canny edge detector.The results show that the proposed algorithm can effectively reduce the structure seams,and has robust segmentation against changing illumination and itmakes themosaic imagesmore natural.
seamless stitching;Canny edge detector;multi-resolution fusion
TN911.73
A
1674-2109(2016)06-0065-05
2016-04-11
莆田学院育苗基金资助项目(2014057)。
陈淑清(1977-),女,汉族,讲师,主要从事视频运动目标检测、图像拼接的研究。
