横向风对浮力扩散火焰的振荡影响研究
2016-11-08王静舞
江 澄,方 俊,王静舞,商 蕊
(中国科学技术大学火灾科学国家重点实验,合肥,230026)
横向风对浮力扩散火焰的振荡影响研究
江 澄*,方 俊,王静舞,商 蕊
(中国科学技术大学火灾科学国家重点实验,合肥,230026)
火焰振荡频率是火灾科学研究领域的一个重要基本参数,对横向风下火焰振荡频率的研究可以为火灾图像探测的参数设置提供理论依据。针对浮力扩散火焰(0.610-5<弗洛德数Fr<210-2,102<理查德森数Ri<105),本研究将横向风条件下火焰结构假设为倾斜的柱状,通过对燃烧产生的浮力和横向风产生的拖曳力进行动力学分析,得出横向风条件下火焰振荡频率表达公式。结合实验结果得出,火焰振荡频率的理论值和实验值均随拖曳系数的增大(即外界风速的增加)而增大,但实验值的上升趋势较理论值平缓.这是因为公式忽略了风速对火焰温度和系数K的影响。
横向风,浮力扩散火焰,振荡频率,拖曳系数
0 引言
研究表明,火焰振荡现象往往伴随着涡旋的形成,而涡旋的形成会增强火势,因为涡旋把新鲜空气卷吸到火羽流中,使羽流中燃料燃烧更充分[1,2]。外界风存在下火焰形态会发生明显改变,火焰振荡特性也会有所不同且更加复杂,这会降低火灾探测报警中图像探测的准确性。
火焰振荡现象是由浮力诱导的空气卷吸引起的,不少学者对静止环境下浮力扩散火焰振荡频率进行了研究,得出火焰振荡频率f与燃烧器直径D的0.5次方的倒数成正比[3]。Cetegen和Ahmed[4]根据伯努利方程并结合实验得出火焰振荡频率随着理查德森数Ri的增大而减小。他们还通过改变co-flow环境密度来改变浮力从而发现浮力增大,振荡频率也增大[5]。胡等[6]在对中小尺寸乙醇油池火的研究中发现三种火焰不稳定性模式,分别为瞬态Rayleigh-Taylor(R-T)不稳定性、常态R-T不稳定性和膨化不稳定性,并且研究得出各模式时频率依次增大。
经过大量国内外文献调研,对静止环境下火焰振荡现象的研究已初步形成体系,但对环境风下火焰振荡现象的研究非常匮乏,且研究方向主要集中在火焰倾角、火焰辐射等方面。尽管如此,对有风条件下火焰其他特性的研究对火焰振荡特性的研究也提供了很多思想借鉴和理论依据。
Pipkin和Sliepcevich[7]将火焰形状假设成圆柱形,利用动量守恒得出外界风条件下浮力驱动扩散火焰倾斜角度的表达式。Galant等[8]在对较大尺寸浮力主控火焰的研究中,假设压力变化仅由浮力引起并忽略沿射流轴线方向的扩散辐射通量,发展了外界风条件下辐射计算模型(三维稳定抛物线模型)。Morvan等[9,10]采用有限体积法、湍流燃烧模型中的k-ε-g模型等模拟外界风下射流扩散火行为,利用输运方程描述碳黑体积分数,模拟结果显示火焰的行为主要受外界风与火焰上方的浮力流两者共同主导。
火焰振荡现象本质来源于两种机制:一是瑞利-泰勒不稳定性(Rayleigh-Taylor instability)机制,这种机制指的是两种不同密度流体在交界面上低密度流体向高密度流体推进时出现的不稳定现象[11];二是开尔文-亥姆霍兹不稳定性(Kelvin-Helmholtz instability)机制,这种机制指的是由一种连续流体中出现速度剪切或两种流体交界面上存在速度差而引起的不稳定现象[12]。这种速度差包括横向风与射流的速度差以及射流的轴向速度差。Megerian和Davition[12]研究认为对于横向风纯射流,当动量通量比R=(ρjuf02)/(ρwuw2)<3.5,存在自诱导全局振荡现象。R-T与K-H这两种机制皆能引起火焰的振荡现象,由此可知横向风下火焰振荡频率特性是客观存在并且相关研究是有必要的。
有风条件下火焰振荡现象耦合了浮力和横向风的共同作用,从目前的研究来看,对有风条件下火焰振荡的发生机制、动力学理论分析方面还比较欠缺。因此,本文针对浮力驱动扩散火焰(6×10-5<弗洛德数Fr<2×10-2,102<理查德森数Ri<105),耦合横向风对火焰振荡频率的影响,对有风条件下火焰振荡现象进行动力学分析并得出其振荡频率表达式,并与实验结果进行对比分析。
1 火焰振荡频率动力学分析
在横向风作用下,火焰会发生倾斜,火焰振荡频率会发生改变。为了进行有风条件下火焰振荡频率动力学分析,假设研究对象中的流体均为不可压缩的无粘性流体;火焰形状为圆柱形;火焰边界内热气体上升速率在径向上分布均匀。横风条件下火焰结构模型如图1所示。

图1 横风条件下火焰结构模型Fig.1 Diagram of flame configuration in cross-wind.
由水平方向动量定理有mwuw=Fwdt,即ρwuwAdtuw=Fwdt。这里用通过火焰圆柱体中心轴线的横截面积近似代替与横向风垂直的火焰横截面积来简化火焰振荡频率公式的求解。由此可得不同风速对火焰产生的水平拖曳力为:
(1)
式中:ρw为空气密度(kg·m-3),mw为流经火焰表面的空气质量(kg),A为通过火焰圆柱体中心轴线的横截面积(m2),几何因子KG=df/Lf,df为火焰直径(m),Lf为火焰长度(m),uw为横风风速(m·s-1)。
在静止环境下,浮力扩散火焰振荡频率主要受浮力影响,火焰中轴线上的速率随高度增加不断增大,而横向风存在时,在浮力和水平拖曳力的共同作用下,火焰中轴线会发生倾斜。由受力平衡分析可得有风条件下火焰中轴线上燃料的加速度和速率分别为:
(2)
(3)

(4)
在浮力作用下,热气体伴随着一定的加速度从燃烧器出口流出,不断聚集在一个燃烧器直径的高度范围内并产生环形涡旋;环形涡旋在对流的作用下流向火焰下游;而此时,下一个环形涡旋又开始形成,由此循环就形成了火焰振荡现象[4]。在Cetegen的研究中,假设火焰环形涡旋向火焰下游的对流速度与火焰中轴线上的热气体速率成正比[4],则有如下关系式:
(5)

(6)

(7)
整理可得火焰振荡频率表达式如下:
(8)

(9)
将公式(9)代入系数Cw中,即可用弗洛德数Fr代替火焰长度变量得系数Cw表达式为:
(10)
2 实验设计
所有实验均在中国科学技术大学火灾科学国家重点实验室现有大型燃烧风洞实验平台中完成。该风洞全长约20 m,分为动力段、加热段、收缩段和实验段。实验台架安置在长6 m、截面长1.8 m×1.8 m的实验段,如图2所示。风洞可提供风速为0.5 m·s-1~15 m·s-1,实验段风速湍流波动强度小于2%。本实验中设计四个风速工况,分别为1.2 m·s-1、1.7 m·s-1、2.2 m·s-1和2.6 m·s-1。风速由四通道热线风速仪测得。

图2 实验装置俯视图 Fig.2 Top view of experiment setup
丙烷气体由于具有高亮度的优点被作为实验燃料,密度为1.808 kg·m-3。丙烷气体流量通过Alicat气体质量流量控制器进行控制,实验中丙烷火焰热释放速率为15 kW,各工况弗洛德数在0.6~13之间,处于浮力主控范畴。丙烷气体通过燃烧器内部的玻璃珠和蜂窝芯进行均化,燃烧器直径分别为0.05 m、0.075 m、0.106 m、0.13 m和0.15 m,燃烧器结构图见图3。

图3 燃烧器结构图Fig.3 Diagram of burner structure
为了线动态观察和捕捉横向风条件下丙烷浮力扩散火焰燃烧过程,CCD彩色摄像机(25 fps)和Photron高速摄像机被用于相关图像信息的采集,图像采集频率为2000 fps,采集时间为2秒,所采集信息用于分析火焰脉动现象,计算火焰振荡频率。火焰振荡频率的测量根据火焰图像相关性原理,利用Matlab软件提取每帧火焰图像中的火焰长度作为每帧图像所对应的相关系数,然后对提取的一系列火焰长度进行快速傅里叶分析(FFT),可以得到根据火焰长度变化周期转换的火焰振荡频率[15]。火焰温度通过七根均匀分布在火焰中轴线上的K型铠装快速响应热电偶测得,热电偶探头直径为1 mm,测量范围为50 K~1200 K,不确定度小于0.75%,响应时间小于1 s,各工况火焰温度实验测量值如表1所示,实验结果分析采用修正后的火焰温度。实验重复率为3次。

表1 各工况火焰温度实验测量值(K)
3 结果与讨论
图4为不同风速下高速摄像机采集的一个火焰振荡周期序列图。从图4中可以看出,由于横向风的存在,火焰发生倾斜,且随着风速的增大,火焰倾斜程度越大;火焰振荡现象没有无风情况时明显,涡旋的生成部位从无风条件下的火焰根部向下游移动。
将公式(8)进行简化,可得:
(11)
即:
(12)
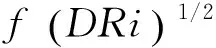
(13)

图4 不同风速下火焰振荡周期(一个周期t0)高速序列图Fig.4 Sequential high speed flame images in different cross-wind speed (a cycle t0)
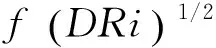
由拟合结果可得K值约为0.35,假设密度比ρw/ρf在3~5,则C值的范围为0.18~0.24,C值小于1说明全局漩涡的对流运动速率相对火焰轴向速率小。无风环境时,C值范围为0.3~0.5[4],有风条件下C值范围小于无风情况C值范围,说明横向风的存在会增强火焰卷吸,使火焰与空气混合程度增大,火焰轴向速率减小,使火焰振荡频率相对于不考虑卷吸影响得出的火焰频率在整体上更小。
由此可得不同直径下火焰振荡频率f和拖曳系数Cw的关系趋势图如图6所示。
从图6中可以看出,实验数据和理论数据均有较好的吻合,随着拖曳系数的增大,火焰振荡频率也随之增大,即随着风速的增大,火焰振荡频率增大。另外也可以看出,实验数据的上升趋势较理论数据平缓,特别是在拖曳系数Cw较大时(风速uw较大时),理论值会稍高于实验值。这是因为这里将K假设为一定值0.35,但当风速增大到一定程度,火焰温度不升反降,使K值减小。随着风速uw增大,系数Cw增大,K减小,两者耦合使得火焰振荡频率随着风速增大而增大的趋势变得平缓。另外,从图6中可以看出,随着燃烧器直径的增大,火焰振荡频率是减小的,这与无风条件下火焰振荡频率随直径增大而减小的趋势是一致的。

图和关系图Fig.5 Relationship of
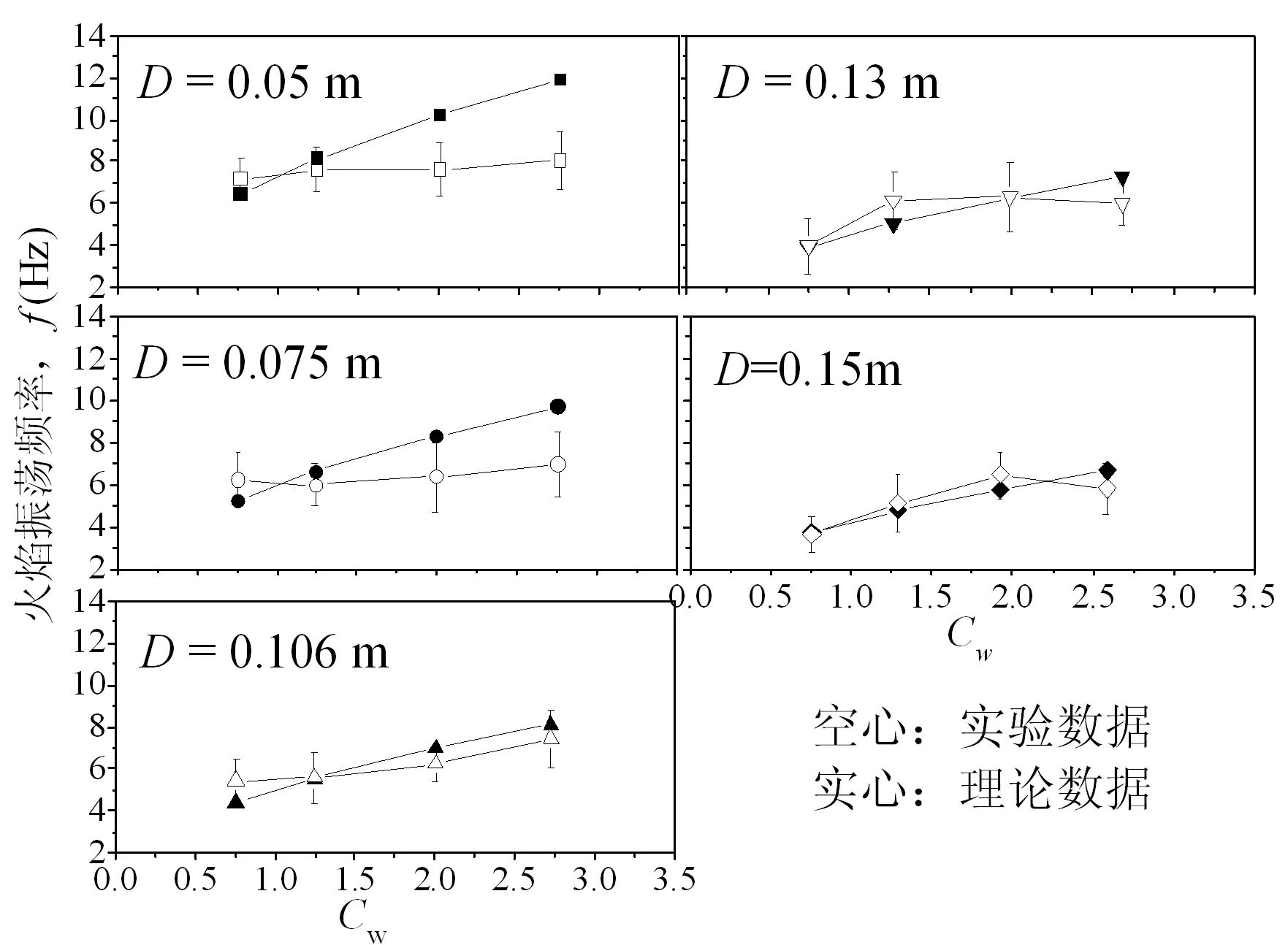
图6 不同直径下火焰振荡频率f和拖曳系数Cw关系图Fig.6 Relationship of flame oscillation frequency f and drag coefficient Cw
4 结论
本研究根据动量定理,综合考虑浮力和横向风对火焰振荡频率的影响,得出横向风条件下火焰振荡频率表达公式,结论如下:
(1)有风条件下火焰振荡现象没有无风情况时明显,涡旋的生成部位从无风条件下的火焰根部向下游移动。
(3)火焰振荡频率会随着拖曳系数Cw的增大而增大,即随着外界风速的增加,火焰振荡频率呈增大趋势,但实验数据的上升趋势较理论数据平缓。这是因为理论公式忽略了风速对火焰温度和系数K值的影响。另外,火焰振荡频率随着直径D的增大而减小,与无风条件下的趋势一致。
本研究中火焰轴向速率在浮力作用下沿火焰轴向下游方向逐渐增大,并没有考虑空气卷吸使火焰轴向速率变小的影响[16],而是将空气卷吸的影响通过实验拟合涵盖在系数C中。考虑卷吸作用使得火焰振荡的理论化变得更加复杂,有待更进一步的理论分析和实验研究。
[1] 霍然, 等.建筑火灾安全工程导论[M].合肥:中国科学技术大学出版社, 1999.
[2] 黎昌海, 等. 封闭空间油池火火焰振荡特性研究[J]. 中国科学技术大学学报, 2010, 40(4): 380-386.
[3] Malalasekera WMG, et al. A review of research and an experimental study on the pulsation of buoyant diffusion flames and pool fires[J]. Fire and Materials, 1996, 20(6): 261-271.
[4] Cetegen BM, Ahmed TA. Experiments on the periodic instability of buoyant plumes and pool fires[J]. Combustion and Flame, 1993, 93(1-2): 157-184.
[5] Cetegen BM, Dong Y. Experiments on the instability modes of buoyant diffusion flames and effects of ambient atmosphere on the instabilities[J]. Experiments in Fluids, 2000, 28(6): 546-558.
[6] Hu LH, et al. Flame necking-in and instability characterization in small and medium pool fires with different lip heights[J]. Combustion and Flame, 2015, 162(4): 1095-1103.
[7] Pipkin OA, Sliepcevich CM. Effect of wind on buoyant diffusion flames[J]. Industrial & Engineering Chemistry Fundamentals, 1964, 3(2): 147-154.
[8] Galant S, et al. Three-dimensional steady parabolic calculations of large scale methane turbulent diffusion flames to predict flare radiation under cross-wind conditions[A]. The Combustion Institute. Twentieth Symposium (International) on Combustion[C]. Pittsburgh: 1985, 20(1): 531-540.
[9] Morvan D, et al. Numerical simulation of turbulent diffusion flame in cross flow[J]. Combustion Science and Technology, 1998, 140(1-6): 93-122.
[10] Morvan D, et al. A numerical investigation of cross wind effects on a turbulent buoyant diffusion flame[J]. Combustion Science and Technology, 2001, 164(1): 1-35.
[11] Sharp DH. An overview of Rayleigh-Taylor instability[J]. Physica D: Nonlinear Phenomena, 1984, 12(1): 3-18.
[12] Megerian S, Davitian J. Transverse-jet shear-layer instabilities. Part 1. Experimental studies[J]. Journal of Fluid Mechanics, 2007, 593: 93-129.
[13] Majeski AJ, et al. Predicting the length of low-momentum jet diffusion flames in crossflow[J]. Combustion Science and Technology, 2004, 176(12): 2001-2025.
[14] Peters N. Turbulent Combustion[M], Cambridge: Cambridge University Press, 2004, 202-203.
[15] 陈志斌,等.基于图像相关性提取的火焰振荡频率[J].燃烧科学与技术,2008,14(4):367-371.
[16] Cetegen BM. A phenomenological model of near-field fire entrainment[J]. Fire Safety Journal. 1998, 31(4): 299-312.
Effect of cross-wind on oscillation of buoyant diffusion flame
JIANG Cheng, FANG Jun, WANG Jingwu, SHANG Rui
(State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China)
This paper studies the flame oscillation frequency in cross-wind for providing theoretical basis for parameter settings of fire detection. For buoyant diffusion flame (0.610-5 Cross-wind; Buoyant diffusion flame; Flame frequency; Drag coefficient 2015-12-30;修改日期:2016-02-26 国家自然科学基金(51576186,51323010)。 江澄(1990-),女,福建龙岩,中国科学技术大学火灾科学国家重点实验室,硕士研究生,火灾探测监测。 江澄,E-mail:jc790791@mail.ustc.edu.cn 1004-5309(2016)-00059-06 10.3969/j.issn.1004-5309.2016.02.01 TK431; X915.5 A
