装配式空心板桥浅企口铰缝应力传递机理研究

张巍， 陈记豪， 赵顺波

(华北水利水电大学,河南 郑州 450045)



装配式空心板桥浅企口铰缝应力传递机理研究

张巍， 陈记豪， 赵顺波

(华北水利水电大学,河南 郑州 450045)

为了优化设计空心板桥的企口铰缝连接，增强装配式空心板桥的整体性，考虑材料非线性、截面接触等因素，建立了某空心板桥的三维有限元分析模型，研究了其铰缝与空心板间的应力、应变对桥梁结构的影响。结果表明：均布荷载作用跨中主要影响范围为横向三片空心板，两个铰缝；铰缝主要靠剪应力传递荷载，同时竖向剪切应力决定剪应力的大小；铰缝纵向传递荷载，本身受拉、压交替变化。

空心板桥;铰缝;剪应力;非线性;单板受力

在装配式混凝土空心板桥的大量病害中,由混凝土铰缝损伤导致的病害占很大比例[1]。铰缝直接关系到空心板梁上部结构的整体受力性能，铰缝病害最极端的情况，将出现空心板“单板受力”，从而导致空心板承受的荷载大于设计荷载，危及桥梁结构安全[2-3]。虽然对于铰缝的研究已经较多[4-5]，但上述问题尚未得到有效的解决。

ABAQUS在土木工程桥梁分析领域应用非常广泛，特别是混凝土塑性损伤模型在混凝土结构分析方面起到很好的效果。工程结构的非线性一般分为材料非线性、接触非线性和几何非线性。对结构的分析计算基本上都会遇到非线性计算不收敛的问题，对于混凝土的黏性系数、膨胀角等参数取值的合理性，都需反复推敲[6]。

本文以一座典型的浅企口缝装配式空心板桥为例，采用ABAQUS软件分析了超载情况下铰缝接触面的受力性能和铰缝破坏过程，以探讨铰缝传力机理。

1　旧桥计算模型

选取G4高速公路安阳—新乡段加宽一期工程某桥进行分析。桥交叉角90°,计算跨度15.5 m，桥宽12.0 m，由6块中板和两侧各2块边板组成。空心板横断面如图1所示。中板横截面尺寸如图2所示。边板除上部结构与中板略有不同外，其他尺寸都一样。

图1　旧桥预应力空心板横断面图

图2　旧桥中板横断面尺寸(单位：mm)

表1　整桥材料特性表

采用ABAQUS软件进行建模计算。空心板和铰缝接触面连接，采用有限元中的surface接触面连接，采用折算弹性模量。考虑接触属性，需要定义3个方向的接触参数，根据试验数据[8]，3个方面的粘结刚度均取10 MPa/mm，切向摩擦系数为0.1，其他参数不变。空心板、铰缝、铺装层均采用8节点6面体实体单元C3D8I网格划分。为便于计算，选取一跨上部结构进行计算，预应力空心板施加空间简支约束。

1.1荷载施加

按车辆荷载中的单个车轮布载，考虑到建模的方便，参考相关文献[9]选择均布荷载作用面积为600 mm×200 mm，施加均布荷载分别为0.5、1.0、2.0、3.0、4.0、5.0 MPa，即分别相当于60、120、240、350、480、600 kN的集中力作用的6种工况荷载作用在第4块空心板跨中的中心位置。如图3所示，把铰缝的4个接触面分别定义为A、B、C、D，将各接触面的中心位置纵向作为提取相关数据的路径。

图3　铰缝接触面数据采集路径

1.2材料属性定义

混凝土采用ABAQUS中的Concrete Damaged Plasticity模型，根据我国规范给出的混凝土受压曲线[10]，拟合混凝土参数。

(1)

式中：σc为混凝土应力；fc为混凝土峰值应力；ac=0.157fc0.785-0.905；x=ξc/ξ0；ξc为混凝土应变；ξ0为峰值应力对应的应变；n=Ec/(Ec-E0)；Ec为弹性模量；Ε0为峰值应力对应的切割模量。

ABAQUS中材料的弹性和塑性性质需要分开定义，弹性阶段的应变为零[11]。铰缝C50混凝土采用塑性损伤模型，参数见表2，并在模型中定义拉伸弹塑性应力-应变曲线和压缩弹塑性应力-应变曲线。软件ABAQUS对于钢筋混凝土结构模型的模拟提供了3种方法：整体式、分离式和组合式[5]。由于模型较大，单元较多，因此采用整体式模型，即将空心板混凝土与钢筋看作一个整体，并采用均化的钢筋混凝土折算弹性模量。折合后的空心板采用C60混凝土，弹性模量为37 232 MPa，泊松比为0.2。

表2　C50混凝土塑性参数

2　空心板与铰缝接触面的应力分布

非线性有限元计算收敛后，提取荷载为600 kN时，空心板桥和铰缝的Mess云图分别如图4和图5所示。由图4和图5可知，第4块空心板跨中荷载作用区域上的表面应力呈正方形分布，然后向四周呈椭圆形传递，数值逐渐降低。这说明空心板通过铰缝传递荷载时，荷载作用位置处数值最大，然后向纵向和横向两个方向递减，这与文献[12]中传统力学分析的结果一致，且辐射范围近似椭圆形分布。

图4　空心板桥的Mess云图

图5　铰缝的Mess云图

6种荷载工况中，均布荷载作用影响区域的分布规律基本一致。仅将荷载作用于S4时SK1—SK7底部中心点的力学特性计算结果列于表3，并绘制不同铰缝底部中心处的横向应力以及挠度的分布，如图6所示。这里，正值表示受压，负值表示受拉。

表3　铰缝受力特性计算结果

图6　铰缝底部中心的横向应力和挠度分布

显然，S4上的力主要通过其两侧的SK3和SK4传递，且荷载主要由S4承担，其挠度值最大。由图4—6和表3可知，均布荷载作用下，铰缝应力传递的范围为：以力作用位置为中心，沿桥梁纵向两端均传递2.5b(b为空心板宽度)，横向沿桥梁宽度方向左右均传递1.5b。同时，S4两侧铰缝竖向应力未呈对称分布，这与传统力法分析和线性有限元分析结果不同，可能是铰缝非线性变形所致。荷载作用于S4跨中位置时，对SK3和SK4力学性能的影响最大。同时，SK3和SK4关于S4对称，因此仅对SK3进行研究即可。分别提取SK3接触面A、B、C、D路径上的横向应力σ1、竖向应力σ2、纵向应力σ3、竖向剪切应力γ1、纵向剪切应力γ2和法向应力γ3的分布规律。

2.1接触面横向应力σ1、竖向应力σ2、纵向应力σ3

由于左、右接触面应力对称，故绘制出左接触面不同位置的应力分布曲线，如图7—8所示。当荷载作用于S4跨中时，横向应力和竖向应力在跨中附近变化最大，应力沿跨中对称分布，均是跨中部位的值最大；然后向两侧迅速下降，其他区域的应力保持值较小，且变化不大。纵向应力沿桥跨方向拉、压交替出现，呈现波形分布，且在跨中位置的值最大。

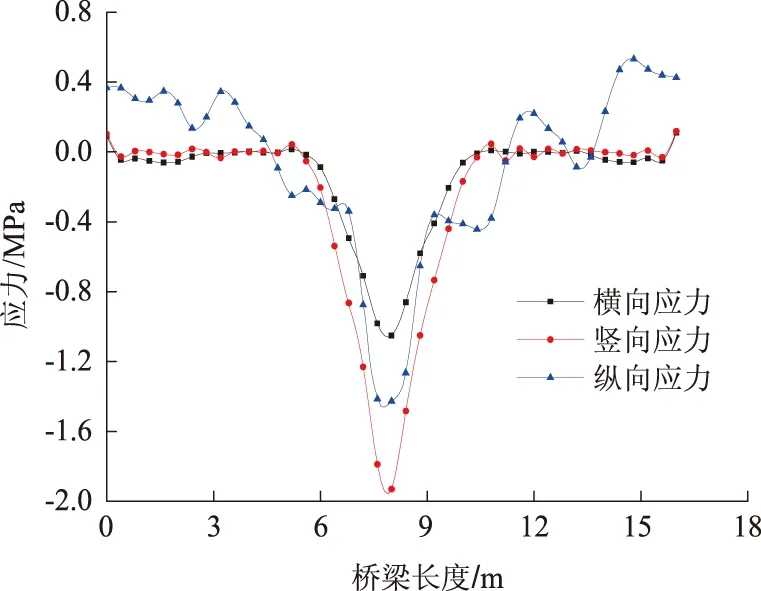
图7　左接触面A应力分布

图8　左接触面B应力分布

跨中截面应力沿接触面方向分布如图9所示。

纵向应力从顶面到底面逐渐增大，在底部达到最大值。横向应力和竖向应力变化基本一致：由顶面到底面先增大后减小，在中间尖点位置取得最大值。接触面上竖向剪切应力的分布基本呈现对称分布，但是数值并不完全对称，这是铰缝非线性变形所致。

图9　左截面应力分布

2.2竖向剪切应力γ1

铰缝左、右接触面沿着桥梁方向的受力机理相同，有限元分析数据相近，因此仅绘制左面竖向剪切应力分布，如图10所示。铰缝接触面在当荷载作用在S4时，竖向剪切应力在跨中的值达到最大，往桥两侧则逐渐减小到零附近。其中跨中附近竖向剪切应力变化较大，沿跨中对称分布，两边呈现变化较小的稳定状态。接触面A和C上的极值比接触面B和D上的大。由纵向应力范围可知，荷载主要影响距离在5 m以内，和前面的分析结果一致。

图10　左面竖向剪切应力分布

左横向截面竖向剪切应力分布如图11所示。铰缝接触面各个截面的竖向剪切应力的变化趋势一致：在接触面A和C上，都是在接触面中间部位达到最大值，然后向两侧减小，至铰缝尖点处的值最小；在接触面B和D上，都呈现出增大的趋势。铰缝右接触面上的竖向剪切应力比左接触面上的变化幅度大，因右接触面更接近荷载作用区域，承受主要的荷载。另外，铰缝在传递荷载时本身也承担一定的荷载，上部承受较大的压力，故增大铰缝接触面面积对其受力更有利。

图11　左横向截面剪切应力分布

2.3纵向剪切应力γ2

由结构受力可知，剪力成对出现，且沿着桥梁纵方向相反，因此仅绘制铰缝左接触面的纵向剪切应力分布，如图12所示。显然，左接触面在跨中处纵向剪切应力为0 MPa，左侧受压，右侧受拉；右接触面同样在跨中出现零点，左侧受拉，右侧受压。两侧接触面均是作用力位置附近应力较大，其余位置基本不受影响。

图12　左面纵向剪切应力分布

铰缝左接触面的横向剪切应力分布如图13所示。

图13　左面横向剪切应力分布

由图13可知，在跨中荷载附近区域，铰缝存在某一截面的纵向剪切应力为0 MPa，然后向两端一边受拉，一边受压。沿着同一接触面的受压区，横向剪切应力数值增大，直至变成受拉区；同样，沿着同一接触面的受拉区，横向剪切应力数值减小，直至变成受压区。左、右接触面变化基本一致。铰缝纵向传递荷载时是受拉、压交替变化的过程。

2.4剪应力

图14　左面纵向剪应力分布

由于左、右截面横向剪应力分布规律相同，这里仅给出左面横向剪应力分布，如图15所示。自上而下接触面A和C的剪应力逐渐降低，接触面B和D的剪应力逐渐增大，在接触面的尖点处达到最小值。铰缝在传递荷载时，在接触面A和C的顶端附近，以及接触面B和D的底端附近，均存在剪应力较大的一段区域，容易破坏。

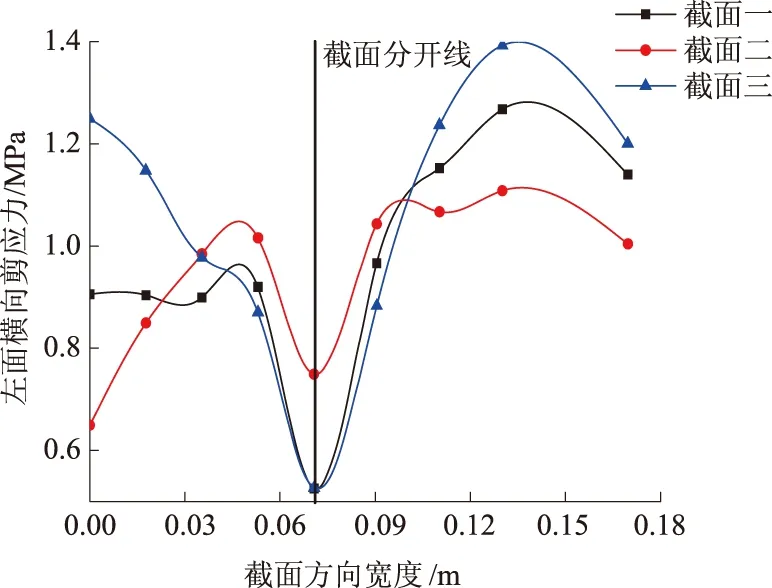
图15　左面横应向剪应力分布

3　铰缝破坏过程

当600kN的荷载作用于S4跨中位置时，选取空心板S4底部中心点绘制其荷载-挠度曲线，如图16所示。为确定空心板桥梁是否出现“单板受力”，提取不同荷载作用下的各空心板跨中底部的挠度，绘制挠度曲线，如图17所示。

图16　荷载-挠度曲线

图17　不同荷载时的挠度曲线

由图16—17可知，铰缝破坏分为3个阶段：①荷载小于345kN时的线弹性阶段，铰缝应力随着荷载的增加呈线性增长，铰缝完好，能均匀传递荷载，桥梁保持较好的整体性能；②荷载位于345～498kN时的屈服阶段，荷载变化与挠度变化较大，空心板和铰缝接触面开始分离，工作性能有较大的变化，铰缝传递荷载能力下降；③荷载达到498kN后，挠度发生突变，剪切失效，铰缝接触面破坏分离，铰缝退出工作，空心板相对位移明显增大，且挠度分布不均匀，此时空心板进入单板受力状态。提取SK3的C和D接触面各应力值列于表4。由表4可以看出，混凝土平均应力变化的塑性阶段是弹性阶段的1.9倍，而屈服阶段是塑性阶段的4.1倍，因此空心板桥已经超出了正常的使用状态。

表4　铰缝三右接触面C和D接触点应力表

4　结语

1)随着荷载的增加，铰缝逐步丧失传递荷载的能力，形成单板受力的情况。

2)均布荷载作用下，力传递范围呈椭圆形分布，作用区域纵、横向长度分别为5倍和3倍的空心板宽度。

3)铰缝接触面横向应力和竖向应力变化一致，中心位置达到最值，与纵向应力不同。纵向应力变化影响桥梁体系的整体工作性能。

4)空心板通过铰缝传递荷载，沿桥梁纵向呈现受拉、压交替的分布。剪力的大小主要由竖向剪切应力决定，受纵向剪切应力影响较小。

5)跨中荷载作用下，铰缝上侧承担较大荷载。铰缝突出部分上侧的顶端和铰缝突出部分下侧底端附近的一段区域内剪应力较大，容易破坏，需要进行加固处理。

[1]林源锋,张勇.典型病害空心板梁使用状态评定及加固方案分析[J].铁道建筑,2012(1):38-40.

[2]杨建中,曲福来,赵顺波.装配式预应力空心板桥面混凝土铺装层病害及防治[J].华北水利水电学院学报，2010,31(1):33-36.

[3]陈记豪,赵顺波,姚继涛.装配式简支空心板桥上部结构整体性的评价[J].混凝土,2012(11):113-118.

[4]刘沛林,时旭东,张天申.装配式钢筋混凝土筒支板梁桥铰缝接触面应力分析[J].特种结构,2010，27(4):20-23.

[5]杨继新.装配式空心板桥铰缝受力性能研究[D].内蒙古:内蒙古工业大学，2009.

[6]刘劲松，刘红军.ABAQUS钢筋混凝土有限元分析[J]. 装备制造技术,2009(6):69-70.

[7]陈记豪,赵顺波,姚继涛.既有预应力空心板桥加宽设计的荷载横向分布计算方法[J].工程力学,2012,29(9):265-271.

[8]刘健.新老混凝土粘结的力学性能研究[D].大连:大连理工大学，2000:77-79.

[9]陈悦驰,吴庆雄,陈宝春.装配式空心板桥铰缝破坏模式有限元分析[J].工程力学, 2014,31(6):51-58.

[10]中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 50010—2010[S].北京：中国建筑工业出版社，2010:209-215.

[11]张劲,王庆扬,胡守营，等.ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构,2008,38(8):127-130.

[12]陈记豪.装配式简支板桥上部结构整体性分析与损伤识别[D].西安:西安建筑科技大学,2011:65-78.

(责任编辑：陈海涛)

The Stress Transfer Mechanism of the Shallow Tongue-Groove Hinge Joints in Precast Hollow Slab Bridge

ZHANG Wei, CHEN Jihao, ZHAO Shunbo

(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

In order to optimize the design of the tongue-and-groove joint connection in the hollow slab bridge and strengthen the integrity of the precast hollow slab, considering the material nonlinearity andcross-sectional contacts and other factors,a three-dimensional finite element analysis model of the hollow slab bridge is built. The influence of the stress and strain among the hinge joints and the hollow slabs on the bridge structure is studied. The results show: under uniform distribution loads the main effected scope is the three transverse hollow slab and two hinge joints; hinge joints mainly transfer the loads by shear stress;at the same time, the vertical shear stress determines the size of shear stress; the hinge joints longitudinally transfer the loads, and it alternates itself by tension and compression.

hollow slab bridge; hinge joints; shear stress;nonlinear; single beam bearing

2016-05-06

2013年郑州市科技攻关重点项目(既有桥梁加宽改造中非规整装配式简支T梁桥荷载横向分布计算理论及应用研究);2014年郑州市科技计划项目(141PPTGG373)。

张巍(1991—),男,河南驻马店人,硕士研究生,从事混凝土结构理论与应用方面的研究。E-mail:xuanshi86@163.com。

陈记豪(1981—)，男，河南泌阳人，讲师，博士，从事混凝土结构理论与应用方面的研究。E-mail:cjh@ncwu.edu.cn。

10.3969/j.issn.1002-5634.2016.05.014

TV334

A

1002-5634(2016)05-0076-06

赵顺波(1964—)，男，河北武邑人，教授，博导，博士，从事混凝土结构理论与应用方面的研究。E-mail:zsb6411@163.com。