基于混沌相空间技术的地下水埋深预测的BP网络模型

许拯民, 刘紫薇, 韩伟伟

(华北水利水电大学,河南 郑州 450045)



基于混沌相空间技术的地下水埋深预测的BP网络模型

许拯民, 刘紫薇, 韩伟伟

(华北水利水电大学,河南 郑州 450045)

随着社会经济的不断发展,地下水开发和利用程度日益增加,造成了地面沉降、地裂缝、海水入侵等一系列环境地质问题。为了探求人民胜利渠灌区地下水位变化的特征,并对地下水位进行合理的预测,在相空间重构理论的基础上,首先使用自相关函数法对灌区地下水埋深时间序列的延迟时间进行求解,然后运用G-P算法求出时间序列的最佳嵌入维数,最后采用小数据量的方法从时间序列中提取出Lyapunuov指数,对灌区地下水埋深时间序列的混沌特性进行研究。并建立基于混沌相空间技术的BP神经网络模型,对灌区2013年地下水埋深进行预测。通过与实际观测值的对比分析知,预测结果合理,预测精度较高。

地下水埋深;相空间重构;混沌;神经网络

在实际的水环境管理工作中,地下水位的预测起着尤为重要的作用。水资源的科学管理和合理开发利用,直接受到地下水位预测结果的影响。如何通过对地下水水位的准确预测来实现地下水水资源的合理配置,制定出有效的措施来防止地下水水位的持续下降,已经成为当前水文地质研究的一个重要问题[1]。很多专家、学者采用了各种方法进行了地下水位的预测,其中传统的地下水位预测方法有有限单元法、有限差分法、回归分析、频谱分析、时间序列分析等[2]。地下水水位的影响因素如降雨量、蒸发量、开采量等都是比较复杂的，且具有很强的不确定性,使用单一的模型来描述地下水位动态变化的趋势性和波动性都是不可能实现的,要想提高地下水位预测的精度,必须研究和运用组合的预测方法。

近年来,一些非线性预测方法相继被应用于地下水位预测中,都取得了较为合理的结果。这些方法中,混沌理论具有很强的代表性[3]。近20年来,国内外学者通过混沌理论对水文演化过程进行了大量的研究分析。D. J. Farmer和Takens提出的重构相空间法[4-5]是在时间序列基础上的混沌分析方法,其原理是将系统长期演化的任一单变量因子序列转化为多维非线性系统,包含了系统中的所有变量长期演化的过程信息,虽然在较长时间内混沌系统的运动轨迹是无序的,但是短期内发散较小,可以进行短期预测[6]。混沌相空间技术与神经网络相结合的这种算法,是通过混沌系统动力吸引子这种特定的轨道来确定网络的输入结构,利用神经网络的非线性映射功能来映射地下水埋深演变规律与其影响因子之间的关系,这种思路与方法很值得研究。

本文采用自相关函数法、G-P算法对人民胜利渠灌区的地下水埋深时间序列进行相空间重构,确定相空间重构所需的延迟时间和嵌入维数等参数,并基于混沌理论,通过小数据量的方法对灌区地下水埋深时间序列的最大Lyapunov指数进行计算。计算结果为正,从而证明了灌区地下水埋深时间序列具有混沌性,且混沌性十分明显。

1　模型构建

1.1混沌时间序列的相空间重构

迄今为止,虽然对于混沌完全严格的定义很难给出[7]，但在研究混沌的运动规律时发现有两个明显的特征:①与确定性系统不同,混沌的外在表现类似于纯粹的随机运动,这就使其长期不可预测;②不同于一般的随机系统,混沌运动在动力学上又具有确定性,这使它在短期内可以进行预测[8]。

地下水的水文系统可以认为是一种混沌系统,其水位变化过程是由低维的混沌吸引子的非线性确定性动力学方法来确定。当对于地下水的水位预测基于一维空间时，由于一维空间无法容纳关联维大于一维的且能够表现出混沌系统规律性的吸引子,故而为了防止所建模型在演化过程中丢失信息而使预测结果不准确,提出了基于时间序列构造一个多维的向量，从而构建一个嵌入空间的方法,这就是Takens等人提出的嵌入式定理。在这种情况下,只要嵌入空间的维数够高,恢复地下水原来的动力学形态以及了解吸引子的演化过程和拓扑结构,就能够对地下水水文系统的未来趋势做出更为准确的预测[9]。在使用这种方法对时间序列进行预测的过程中,必须确定两个关键参数,一个是嵌入维数m,一个是延迟时间τ。

1.2延迟时间的确定

目前,使用自相关函数法[10]求延迟时间τ的方法得到了广泛的应用。此方法简单易懂,且使用方便,得出的结果比较合理,并且采用这种方法对延迟时间τ能够进行独立求解。它的原理是对序列间的线性相关性进行提取，如给定某个混沌的时间序列,当需要确定序列的延迟时间时,可以先写出其自相关函数,一般可用下式计算:

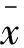
根据上式能够绘制出自相关函数随τ的变化曲线。经过多次的数值试验和研究,得出了以下结论:当自相关系数首次达到0时的τ,就是延迟时间τ。

1.3嵌入维数的确定

嵌入维数m的选取至关重要。当选取的嵌入维数m过小时,会导致重构吸引子无法实现完全打开;而嵌入维数m取值过大时,在建模过程中就会对实测值的要求过高。1983年，Grassberger和Procaccia提出的G-P[11]算法是比较常用且最为合适的。以下为其步骤:

时间序列为{x1,x2,…，xn-1,xn,…}。给定一个较小的m值,重构相空间Y(ti)=[x(ti)，x(ti+τ)，x(ti+2τ)，…，x(ti+(m-1)τ)]，i=1，2，…。

计算关联函数

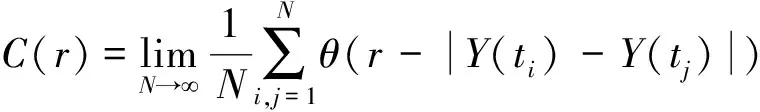
这里r的取值应有一个合适的范围,当r位于该范围内时,吸引子的关联维数D和累积分布函数C(r)呈对数线性关系,即D(m)=lnC(r)/lnr。

根据该对数线性关系,可以拟合求出与m0相对应的关联维数的估计值D(m0)。

增加嵌入维数,重复计算。当关联维数的估计值D(m)随着m的增长出现饱和时,得到的D就是吸引子的关联维数。

当求取时间序列的嵌入维数时,先是给定一组从小到大的m值,并选取适当的r,然后根据上面所叙述的方法,绘制出一簇lnC(r)随着lnr变化的曲线,并通过最小二乘法求出曲线中直线段的斜率,这些斜率即不同嵌入维数m所对应的关联维数D。当关联维数不再随着m的增大而变化,即达到饱和时,此时的m值就是重构相空间的最佳嵌入维数。

1.4Lyapunov指数的确定

判别一个系统是否具有混沌性,最直观有效的方法是利用最大Lyapunov指数。它定量描述了混沌系统对初始不确定性的放大率,在求解上也简单易行。当最大Lyapunov指数为正时,表明系统一定具有混沌的特性。此次研究求解最大Lyapunov指数所使用的方法是小数据量方法。以下是小数据量方法的具体步骤:

1)对时间序列{x(ti),i=1,2,…,N}进行傅里叶变换,计算出平均周期。

2)计算出延迟时间τ和嵌入维数m。

3)根据延迟时间τ和嵌入维数m重构相空间{Yj,j=1,2,…,M}。

5)对相空间中每个点Yj,计算出该邻点对i个离散时间步后的距离dj(i):

6)求出y(i),即

式中q为非零dj(i)的数目,并用最小二乘法做出回归直线,该直线的斜率就是最大Lyapunov指数。

2　基于相空间的BP网络模型

在非线性信号处理领域中,将混沌理论与神经网络进行结合是一种新型的方法。混沌是非线性模型所产生的复杂的不规则的动力学行为,是一种非线性动力学系统。混沌性内部的这种来自于非线性的确定的规律性,能够表现出时间序列在时间延迟状态空间上的相关性,这种特性使得系统具有能够记忆几乎所有状态空间变量的痕迹的能力,并且使用一些通常的解析方法来进行理解和表达时十分不易,而神经网络恰恰可以对这种信息进行处理。基于混沌的BP网络模型的建立过程如下。

在重构相空间中,设当前状态为

Y(ti)=[x(ti),x(ti+τ),x(ti+2τ)，…，

x(ti+(m-1)τ)],

时间延迟τ后的状态为

Y(ti+τ)=[x(ti+τ),x(ti+2τ),…，

x(ti+mτ)]。

选用嵌入相空间的最佳嵌入维数作为神经网络的输入节点,Y(ti)表示时间序列,Y[i]为输入层节点的第i个输入,所得网络模型如下:

Y[i]=y(t+(m-1)τ),

式中:i为神经网络的输出;ω为网络连接权重;f为非线性tansig函数,表达式为：

采用误差反向传播的前馈网络(BP网络),网络层数选为3层,输出层采用线性函数为传递函数。网络输入为x(ti),x(ti+τ),x(ti+2τ),…,x(ti+(m-1)τ),共m个输入。设置m个隐层单元节点,输出为x(ti+mτ)。

为了避免网络陷入局部极小值,减少训练时间,采用附加动量和梯度下降混合算法。具体步骤如下：

1)网络的建立。由已经通过计算得出的嵌入维数m作为网络的输入个数,根据以上步骤建立网络。

2)网络的学习。用BP网络对重构后的混沌时间序列进行拟合。

3)采用学习好的BP网络来预测未来值。

3　实例应用

3.1研究区概况

人民胜利渠灌区的地理位置在河南省新乡市,是中华人民共和国成立以后在黄河中下游建立的首个引取黄河水进行灌溉的大型自流灌区。灌区南面靠近黄河,向北可以到达卫河一带,西边以共产主义渠为界,东部沿黄河故道延伸到柳卫、丰庄一带。灌区的土地面积为14.87万hm2。其中包括耕地面积9.92万hm2,面积占有率66.74%；灌区内河道、湖塘等一些水域的面积为0.70万hm2,面积占有率4.70%；灌区内城镇的面积为3.13万hm2,面积占有率21.08%；其余的面积为1.11万hm2,面积占有率7.48%。自1952年建成以来,灌区不仅对新乡、焦作、安阳等9个县(市、区)47个乡(镇)的9.9万hm2的农田进行灌溉,而且还承担着向新乡市供水和必要时向安阳、天津送水补源的重任。

人民胜利渠灌区位于东经113°31′～114°25′,北纬35°00′～35°30′,位于我国东部季风区的中纬度地带,属于暖温带大陆性季风气候。灌区所处位置四季分明：春季短暂干旱,且多风沙；夏季炎热多风,雨水较多；秋季凉爽,适于农作物的生长；冬季寒冷干燥,降水稀少。灌区平均年降雨量为578 mm,降雨量在年内分布极不均匀,并且发生降雨的月份通常为夏季的6、7、8月份,占全年降雨量的60%～70%,其他季节降雨稀少,比较干旱。夏秋两季经常出现旱涝交替的现象,多年平均蒸发量为1 864 mm。降水年变率一般在20%～30%[12]。灌区土壤主要以潮土为主,其面积为灌区土壤总面积的75%左右,风沙土占灌区土壤总面积的12.5%,盐土占8%。

3.2相空间重构

将灌区1993—2013年共252个月的数据进行整理,根据自相关函数的方法对相关系数进行计算,并做出自相关函数关于延迟时间的变化曲线,如图1所示。

图1　地下水埋深自相关函数变化曲线

由图1可知,自相关函数具有十分明显的衰减现象。延迟时间一般取自相关函数首次过零点时所对应的值。由图可知,延迟时间τ为4个月。

取嵌入维数m=1,2,…,根据前面所求得的延迟时间τ,分别做出与不同m所对应的lnC(r)-lnr曲线，如图2所示；然后根据图2中曲线的直线段斜率,做出D-m关系曲线，如图3所示。

图2　月地下水埋深lnC(r)-lnr关系曲线

图3　月地下水埋深D-m关系曲线

由图3可以看出,在m=7以后,关联维数D不再随着m的增大而增加。这就表明所求的嵌入维数m是饱和嵌入维数,即m=7就是所求的饱和嵌入维数，即最佳相空间嵌入维数。

根据以上方法计算出灌区地下水埋深时间序列的参数，见表1。

表1　地下水埋深时间序列参数

从表1中可以看出,灌区地下水埋深时间序列最大Lyapunov指数为0.025,大于0,这就说明灌区地下水埋深序列具有明显的混沌特征。

根据前面求得的延迟时间和最佳嵌入维,选取灌区1993—2012年的地下水埋深数据进行相空间重构和神经网络建模,对2013年地下水埋深数据(作为模型检验)进行预测。BP神经网络由输入层、输出层和隐含层3层结构组成,采用Sigmoid函数作为激励函数。

灌区2013年地下水埋深预测值与实测值的对比见表2。

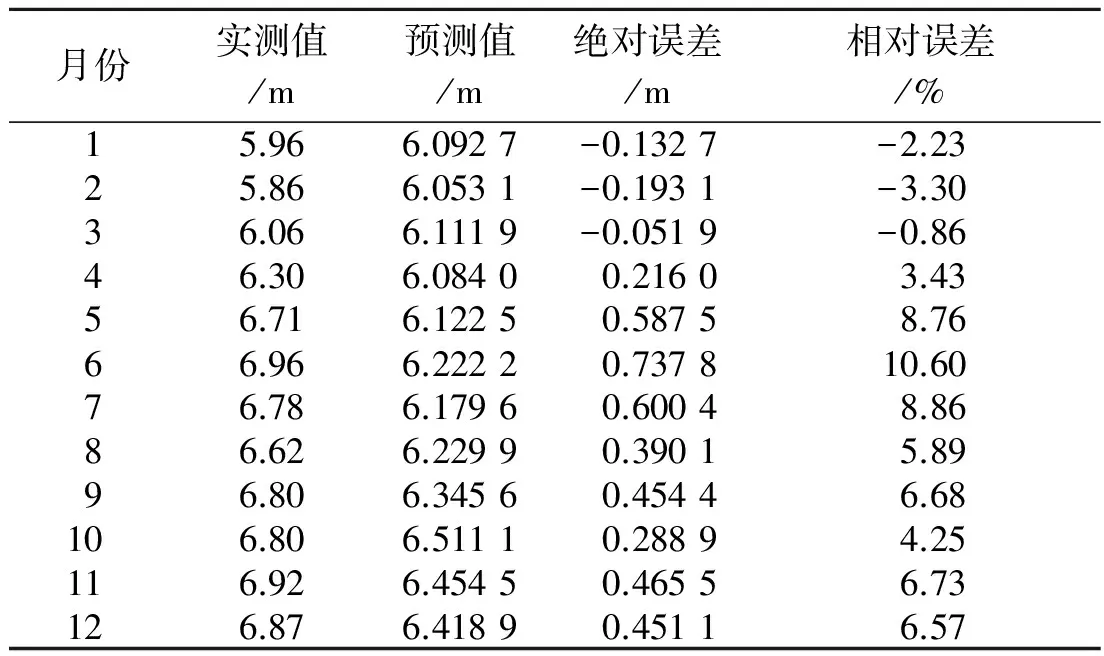
表2　模型预测值与实测值对比表

根据文献[13]，在相对误差为10%以下时为合格[13]。由表2可知，模型预测的最大相对误差为10.6%,平均相对误差为6.3%,合格率为91.7%。模型的预测精度很高,2013年12个月中只有6月份是不合格的。由于6月份属丰水期,随着降雨量的增大,其边界条件的敏感性增强,故预测精度会有所降低。而在枯水期时,降雨量小,月际变化小,所以预测精度高。

4　结语

1)以混沌相空间技术为基础,对灌区月地下水埋深时间序列的最大Lyapunov指数进行求解,结果为0.025。最大Lyapunov指数为正值,表明灌区月地下水埋深时间序列具有混沌特性,在此基础上,能够进行短期的预测。

2)以混沌相空间技术为基础,通过与BP网络模型的结合,建立了基于混沌相空间技术的BP网络模型,并建立了人民胜利渠灌区月地下水埋深时间序列的网络模型,得到的预测结果表明该网络模型预测精度较高。建立BP网络模型,确定模型的输入单元数是难题,本文以混沌空间的最佳嵌入维数作为神经网络的输入单元数,解决了这一难题。

3)本次研究由于验证出灌区地下水埋深序列存在明显的混沌特征,故采用混沌的预测方法进行地下水埋深预测，预测的精度较高。

4)合理预测地下水位的变化趋势,可以为灌区地下水资源可持续利用、生态环境安全以及社会经济持续健康发展提供理论基础,为各级行政部门制定灌区地下水水资源规划、农业发展规划、生态环境保护与治理、社会经济发展规划提供决策依据。但是由于混沌系统存在着伪随机性,本次研究仅仅是对时间序列做了短期的预测,对时间序列的长期预测还需要进一步研究。

[1]刘国东,丁晶.运用BP网络预测地下水位[J].西安地质学院学报,1997,19(2):52-57.

[2]赵丹,张天菊,臧红飞.基于灰色马尔可夫链的兰村泉域地下水位预测[J].人民黄河,2015,37(4):69-72.

[3]付强.农业水土资源系统分析与综合评价[M].北京:中国水利水电出版社,2005:8-61,254.

[4]FARMER J D,OTT E,YORKE J A.The dimension of chaotic attractors[J].Phyisca D Nonlinear Phenomena,1983(7):153-160.

[5]TAKENS.Detecting strange attractors in turbulence[J].Dynamical Systems and Turbulence,1990(11):366-381.

[6]李玉霞,吴百海,邢志鹏.单变量时间序列相空间重构及应用研究[J].组合机床与自动化加工技术,2004(2):51-52,55.

[7]高俊杰.混沌时间序列预测研究及应用[D].上海:上海交通大学,2013:6-7.

[8]潘捷,陈丹霏,王凌云.基于相空间重构参数优化的风电功率混沌属性判定[J].电气开关,2015,53(2):14-18.

[9]丁晶,王文圣,赵永龙.长江日流量混沌变化特性研究Ⅱ:相空间嵌入维数的确定[J].水科学进展,2003,14(4):412-416.

[10]易锦燕,黄雪丽.基于混沌时间序列线性回归预测模型的供应链绩效评价[J].统计与决策,2015(22):44-46.

[11]胡国杰,魏晓妹,蔡明科,等.混沌-支持向量机模型及其在地下水动态预报中的应用[J].西北农林科技大学学报(自然科学版),2011,39(2):229-234.

[12]何宏谋,张永.黄河下游引黄灌区水资源利用研究[J].人民黄河,1996(8):41-43.

[13]张先起,梁川,刘慧卿.基于混沌相空间技术的输沙量预测BP网络模型[J].水力发电学报,2007,26(1):24-27.

(责任编辑：陈海涛)

BP Network Model of Groundwater Prediction Based on Chaos Phase Space Technology

XU Zhengmin, LIU Ziwei, HAN Weiwei

(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

With the continuous development of social economy, the exploitation and utilization of groundwater is increasing, resulting in land subsidence, ground fissures, seawater intrusion and a series of environmental and geological issues. In order to explore the characteristics of the underground water level change in the irrigation area of People Victory Canal and forecast the underground water level reasonably, based on the theory of phase space reconstruction, the chaos characteristics of time series of the groundwater table in the irrigation area is studied. Firstly， the autocorrelation function method is used to evaluate the delay time, then the GP algorithm is used to evaluate the optimal embedding dimension, and lastly, the method of small amount of data is used to extract Lyapunuov index in time series, and BP neural network model based on chaos phase space technology is established. Furthermore, the groundwater table in 2013 in the irrigation areais forecasted.By comparison with the observed value of the analysis, some reasonable prediction results and higher prediction accuracy are obtained.

groundwater depth; phase space reconstruction; chaos; neural networks

2016-04-26

许拯民(1964—),男,河南长葛人,副教授,硕士,从事水资源管理方面的研究。E-mail:562379421@qq.com。

10.3969/j.issn.1002-5634.2016.05.011

TV211.1+2

A

1002-5634(2016)05-0063-05