组装商损失厌恶情形下组装供应链协调

付 红，马永开，唐小我

（电子科技大学经济与管理学院，四川成都611731）

组装商损失厌恶情形下组装供应链协调

付 红，马永开∗，唐小我

（电子科技大学经济与管理学院，四川成都611731）

针对由多个风险中性供应商和单个损失厌恶组装商构成的组装供应链.给出了批发价格契约下各节点企业的均衡策略，发现组装商的最优订货量小于集中化决策下的最优订货量.在此基础上，数值分析表明：当零部件种类数给定时，组装商损失厌恶系数越大，组装商的最优订货量越低；并且随着零部件种类数的增加，组装商损失厌恶系数对组装商的最优订货量的影响程度增大.当组装商损失厌恶系数给定时，零部件种类数越多，组装商的最优订货量也越低；并且随着组装商损失厌恶系数的增加，零部件种类数对组装商的最优订货量的影响程度也增大.引入价格补贴策略设计了协调契约，并通过数值分析，对协调契约的有效性进行了验证.

组装供应链；损失厌恶；价格补贴；协调

1 引 言

目前关于供应链的研究大多都是假设决策者是风险中性的，然而在随机市场需求环境下，风险是必然存在的；即使面对同一个管理问题，由于不同的决策者可能具有不同的风险偏好态度，使得所作的决策往往也因人而异.例如，Fisher等［1］观察到服装制造商的实际订货量偏离了期望利润最大化所对应的决策点.Schweizer等［2］通过实验研究发现大部分报童的订货量较理论研究中风险中性报童的订货量要低.因此，风险中性假设并不能完全刻画决策者的决策行为.

近年来，一些学者在供应链研究中意识到决策者风险中性假设的局限性，开始采用金融理论中的前景理论（prospect theory）、下行风险（downside-risk）、均值方差（mean-variance）以及条件风险价值理论（CVaR）等工具来分析风险厌恶决策者的决策行为.现有关于有风险厌恶决策者参与的供应链研究大多考虑的是供应链中只存在一个供应商.例如，Wang等［3］基于前景理论研究了零售商损失厌恶情形下供应链的协调问题. Gan等［4］基于下行风险理论研究了零售商下行风险厌恶情形下供应链的协调问题.Choi等［5］基于均值方差理论研究了供应商和零售商风险规避情形下供应链的协调问题.闻卉等［6］基于条件风险价值理论研究了供应商和零售商风险规避情形下供应链的协调问题.文献［3-6］的研究都是假设供应链中只存在一个供应商和一个零售商.此外，史成东等［7］基于下行风险理论研究了由一个风险中性供应商、一个下行风险厌恶分销商和一个下行风险厌恶零售商构成的三层供应链的协调问题.李绩才等［8］基于前景理论研究了由一个风险中性供应商和多个损失厌恶零售商构成的供应链的协调问题.Chen等［9］基于条件风险价值理论研究了由多个生产替代产品的风险规避供应商和单个风险规避零售商构成的供应链协调问题.上述文献虽然对有风险厌恶决策者参与的不同结构供应链进行了探讨，但文献［3-8］的研究都是在供应链中只存在一个供应商的假设下建模的；文献［9］考虑的多个供应商生产的产品是替代的.因此，这些研究都隐含的假设最终产品的生产可由一个供应商单独完成.

在组装供应链（assembly supply chain［10］）中，一个供应商只能生产出最终产品组装所需的某一种或几种零部件.零部件的互补性增加了组装供应链研究的复杂性.现有关于组装供应链的研究主要包括两方面.一方面，采用合作博弈理论来分析供应商间的联盟形式问题.这些研究假定供应商之间可以随意结盟，并且联盟内的供应商一起对联盟内的零部件进行定价.例如，Granot等［11］对推式和拉式供应链中供应商间的联盟形式问题进行了研究.研究表明：在推式供应链中，当供应商都有远见时（farsighted），所有供应商才会结成一个大联盟（grand coalition）；而在拉式供应链中，无论供应商是否有远见，他们都将结成一个大联盟. Nagarajan等［12］和Soi［13］研究了决策者市场力量结构对供应商联盟形式的影响.此外，Yin［14］指出供应商间的联盟形式还受市场需求函数类型的影响.

关于组装供应链的另一方面研究较为丰富，这类研究主要是采用非合作博弈理论研究节点企业的均衡策略以及供应链协调问题.例如，Fang［15］研究了产能决策问题.Kalkancı等［16］和罗定提等［17］研究了价格决策问题.供应链中的双重边际效应使得分散化决策下的系统利润要低于集中化决策下的系统利润.Du等［18］研究了因分散化决策所导致的组装供应链系统“效率损失”.为避免这种“效率损失”，Gerchak等［19］首次对组装供应链的协调问题进行了研究.随后，Gurnani等［20］研究了供应商产出随机情形下组装供应链协调契约的设计问题.Yang等［21］研究了供应商交货期不同情形下组装供应链协调契约的设计问题.文献［10-21］假设组装供应链决策者都是风险中性的.此外，付红等［22］研究了供应商损失厌恶情形下组装供应链协调契约的设计问题.

事实上，在市场需求不确定的情形下，根据零部件的库存风险承担方不同，可将组装供应链划分为推式系统和拉式系统.在推式系统中，零部件的库存风险是由组装商承担；而在拉式系统中，零部件的库存风险是由供应商承担［11］.推式系统和拉式系统在现实生活中都是大量存在的.例如，日本的制造商往往采用拉式系统进行生产；而美国以及欧洲国家的制造商却大多采用推式系统进行生产［23］.然而，现有关于组装供应链的研究大多都没有考虑决策者的风险厌恶态度，文献［22］虽然研究了损失厌恶供应商参与的组装供应链，但该论文考虑的是拉式系统.鉴于此，本文以推式系统为研究背景，建立了组装商损失厌恶的组装供应链模型.首先研究了各节点企业的最优决策问题，然后着重分析了协调契约的设计.在有损失厌恶决策者参与的供应链协调刻画方面，本文借鉴文献［3，4］等的研究思路，将供应链整体利润最优所对应的订货量作为分散化供应链的协调基准，即协调的目的是克服分散化决策中的双重边际效应以及组装商损失厌恶态度所导致的订货偏离，实现供应链整体利润最优.

2 组装供应链模型

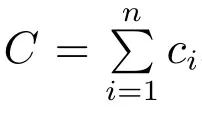
下文中的符号“π”、“U”、“L”分别表示利润、效用、期望损失，右下标符号“c”、“i”、“a”分别表示集中化决策、供应商i、组装商，正上标符号“-”表示引入了价格补贴策略.

针对组装商的损失厌恶特性，本文基于前景理论假定组装商具有以下分段线性效用函数：

式（1）中λ表示组装商损失厌恶系数，λ≥1.当λ=1时，组装商为风险中性的，当λ＞1时，组装商是损失厌恶的，λ越大表示组装商的损失厌恶程度越高.之所以采用分段线性效用函数是因为它不仅能很好的刻画决策者的损失厌恶特性，并且能简化计算.目前这种分段线性效用函数被学术界广泛采用［3，8］.

在集中化决策下，供应链整体的利润为

供应链整体的期望利润为

由式（3）对E（πc）分别求q的一阶和二阶导数，得

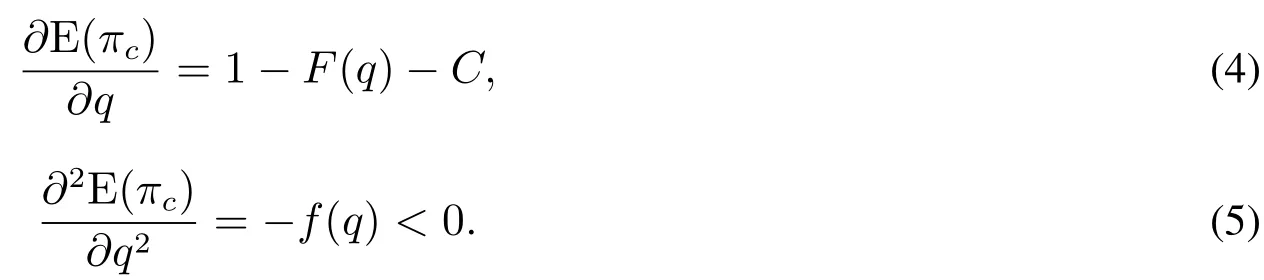
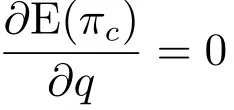
由于供应链整体的期望利润是订货量的凹函数，因此，在分散化决策下，只要组装商的订货量偏离了，系统期望利润都不是整体最优的.

3 分散化组装供应链决策

在批发价格契约下，各决策者都是独立的利益主体，供应商和组装商的决策顺序为：各供应商首先同时给出各自零部件的批发价格wi；组装商然后根据各零部件的批发价格wi确定各零部件的订货量qi［13，19］.由各零部件的组装比例为1∶1∶···∶1可知，理性的组装商将订货q1=q2=···=qn=q.根据上述描述可知，供应商与组装商进行以供应商为主导的Stackelberg博弈.可以通过逆向归纳法对各决策者的最优策略进行求解.

在批发价格契约下，组装商的利润为

记q0为批发价格契约下的盈亏平衡需求量（当需求处在该点时，组装商的利润为零），令πa=0，得到q0=Wq.当x＜q0时，πa＜0；当x≥q0时，πa≥0.因此，组装商的期望损失La、期望利润以及期望效用分别为

通过对式（10）分析可知：组装商的期望效用是由期望利润与期望损失两部分构成.当λ=1时，组装商是风险中性的，其期望效用与期望利润是相等的，即E（U（πa））=E（πa）；当λ＞1时，组装商是损失厌恶的，其期望效用总是小于期望利润，即E（U（πa））＜E（πa），并且当给定期望利润与期望损失时，组装商损失厌恶系数越大，其期望效用越小.

组装商的决策目标是：基于供应商给定的一组批发价格（w1,w2,...,wn）确定订货量q使自身的期望效用最大.由式（10），对E（U（πa））分别求q的一阶和二阶导数，得到

由式（12）可知E（U（πa））是q的凹函数，因此对于供应商给定的一组批发价格（w1,w2,...,wn），组装商的订货量q由下式给出，即

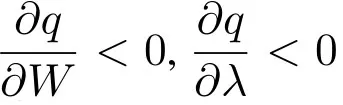
为下文研究方便，当组装商损失厌恶系数λ一定时，记组装商的订货量q与零部件总批发价格W之间的函数关系为q=ψ（W），对应的反函数记为W=φ（q）.接下来，对各供应商如何进行各自零部件的定价进行研究.

由于各供应商都是风险中性的，因此，在批发价格契约下，各供应商的决策目标是：已知组装商的订货量q与零部件总批发价格W在满足式（13）的前提下，通过完全信息静态博弈确定各自零部件的批发价格wi使各自的期望利润最大.供应商i的目标函数为

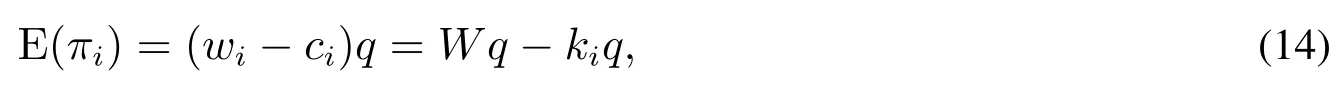
为了得到各供应商的最优批发价格决策，首先给出引理.

引理1 对于给定的一组批发价格（w1,w2,...,wi-1,wi+1,...,wn），供应商i的期望利润E（πi）是q的拟凹函数；并且E（πi）存在惟一的最大值点.

根据引理1的前半部，再结合纳什均衡的存在性定理可知（纳什均衡的存在性定理：在n人的完全信息静态博弈中，若每个参与者的策略空间都是欧式空间上的非空的、闭的、有界的凸集，支付函数是连续的且对策略是拟凹的，那么该博弈必然存在纯策略纳什均衡），供应商间关于零部件批发价格的完全信息静态博弈存在纯策略Nash均衡解.另外，由引理1的后半部分可知，在给定（w1,w2,...,wi-1,wi+1,...,wn）时，供应商i的最优反应是惟一的（供应商i的最优反应为：设定零部件i的批发价格wi使得q=ψ（W）成为E（πi）的最大值点），因此该博弈的Nash均衡解是惟一的［25］.

根据引理1，有下列结论.

定理1 当零部件供应商的个数为n，组装商损失厌恶系数为λ时，在批发价格契约下，组装商的最优订货量q∗与各零部件的最优批发价格分别为

将q∗与分别代入式（10）、式（14），得到批发价格契约下，组装商的期望效用以及供应商i的期望利润，分别记为）与

定理1是对文献［18］中的相关结论的支持和拓展.文献［18］指出，当组装商是风险中性时，各供应商的期望利润是相等的.这是因为每一种零部件都是由每个供应商垄断生产，并且在组装最终产品时，各零部件缺一不可，同等重要［19］.事实上，由式（17）可知，i≠j，即各供应商的边际利润相等，又因为组装商对各零部件的订货量相等，因此，无论组装商是损失厌恶的还是风险中性的各供应商的期望利润都是相等的，即

4 协调契约

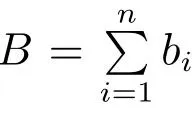
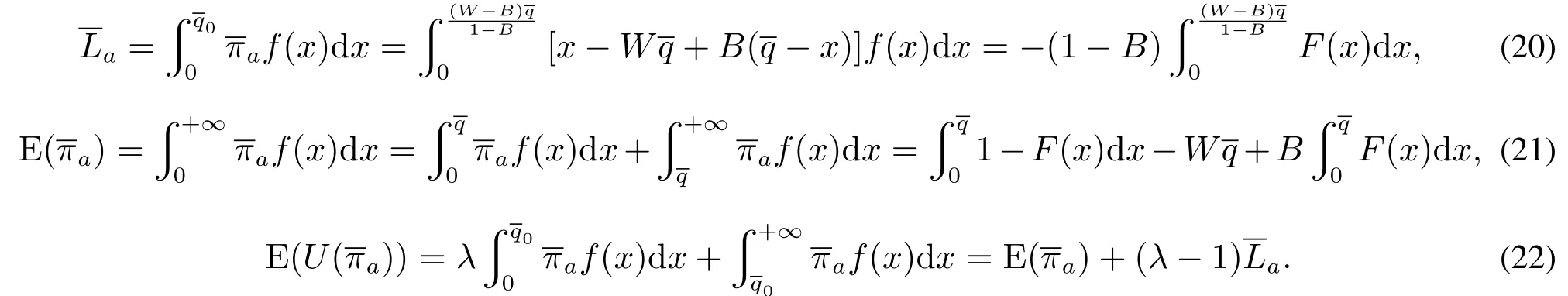
由式（22），对E（U（π））分别求q的一阶和二阶导数，得到

a

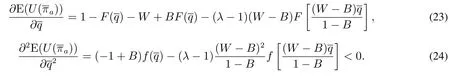
由式（24）可知E（U（πa））是q的凹函数，因此在价格补贴契约｛（w1,b1）,（w2,b2）,...,（wn,bn）｝下，组装商的订货量q由下式给出

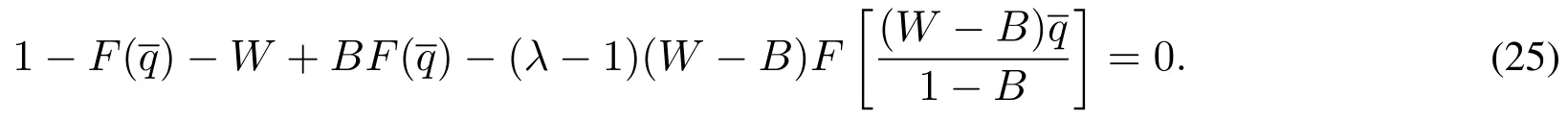
为了得到协调契约，给出下列引理.

引理2 当市场需求的分布函数F（x）与组装商损失厌恶系数λ一定时，存在惟一的常数θ∗∈（0,C］使得

根据引理2，有下列结论.

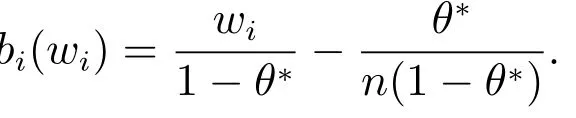
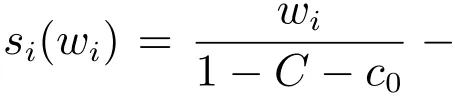
将bi（wi）分别代入式（18）、式（22），得到价格补贴契约｛［w1,b1（w1）］,［w2,b2（w2）］,...,［wn,bn（wn）］｝下，供应商i的期望利润E（i）与组装商的期望效用E（U（a））分别为

根据式（26）、式（27），有下列结论.

定理3 在价格补贴契约｛［w1,b1（w1）］,［w2,b2（w2）］,...,［wn,bn（wn）］｝下，各供应商的期望利润随着各自零部件批发价格增大而增大；组装商的期望效用随各零部件的批发价格增大而减小.

在现实生活中，若一个协调契约能够得以实施，它必须使得各参与者的“利益”得到帕累托改进.由定理3可知，在价格补贴契约｛［w1,b1（w1）］,［w2,b2（w2）］,...,［wn,bn（wn）］｝下，各供应商的期望利润是各自零部件批发价格的增函数，组装商的期望效用是零部件总批发价格的减函数，又因为供应商处于主导地位，因此，令，可求解得到，价格补贴契约｛［w1,b1（w1）］,［w2,b2（w2）］,...,［wn,bn（wn）］｝下，零部件最优总批发价格（对于供应商而言），记为，对应的总补贴价格为.通过下文中的数值分析，可以发现当W=∗时，；再由定理3的前半部分可知，各供应商可以通过调节各自零部件的批发价格实现供应商总期望利润在供应商间的任意分配，即各供应商通过引入价格补贴策略可以在不降低组装商期望效用的前提下提高各自的期望利润.

5 数值分析

通过数值分析的方法，一方面探讨批发价格契约下，各节点企业的最优策略与零部件种类数、组装商损失厌恶系数之间的关系；另一方面对协调契约的有效性进行验证.

由式（6）可知：集中化决策下风险中性决策者的最优订货量为由引理2可知：当组装商损失厌恶系数λ分别为1、1.5、2、3、5时，θ∗的取值分别为0.5、0.449 5、0.414 2、0.366 0、0.309 0.将上述参数代入式（13）、式（16）、式（17），得到批发价格契约下，不同损失厌恶系数λ、零部件种类数n所对应的零部件最优总批发价格W∗以及组装商的最优订货量q∗，见表1、表2.

表1给出了批发价格契约下，不同损失厌恶系数λ、零部件种类数n所对应的零部件最优总批发价格W∗.由表1可知：1）当组装商损失厌恶系数λ一定时，零部件种类数n越多，零部件最优总批发价格W∗越高；并且当组装商损失厌恶系数λ分别为1、1.5、2、3、5时，随着零部件种类数n由2增加到32，零部件最优总批发价格W∗分别增加了18.20%、19.85%、20.91%、22.21%、23.50%，这表明随着组装商损失厌恶系数λ的增加，零部件种类数n对零部件最优总批发价格W∗的影响程度增大.2）当零部件种类数n一定时，组装商损失厌恶系数λ越大，零部件最优总批发价格W∗越低；并且当零部件种类数n分别为2、4、8、16、32时，随着组装商损失厌恶系数λ由1增加到5，零部件最优总批发价格分别降低了4.33%、1.69%、0.52%、0.14%、0.03%，这表明随着零部件种类数n的增加，组装商损失厌恶系数λ对零部件最优总批发价格W∗的影响程度减小.

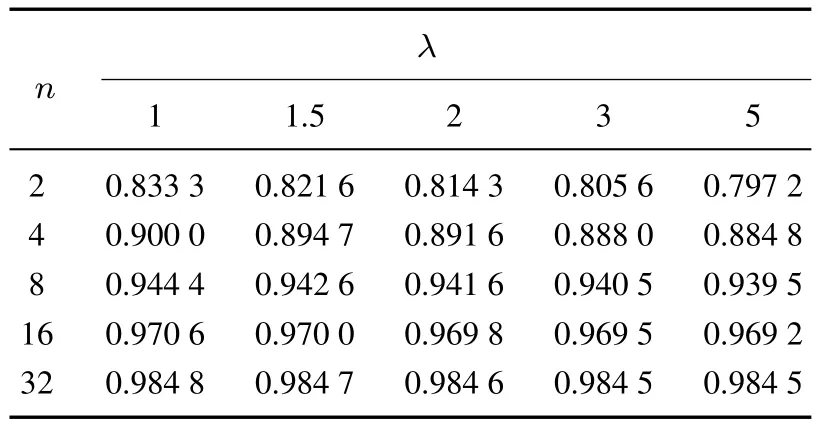
表1 批发价格契约下，不同损失厌恶系数λ、零部件种类数n所对应的零部件最优总批发价格W∗Table 1 Total optimal wholesale prices W∗with different loss-aversion coefficients λ and numbers of components n under a wholesale price contract

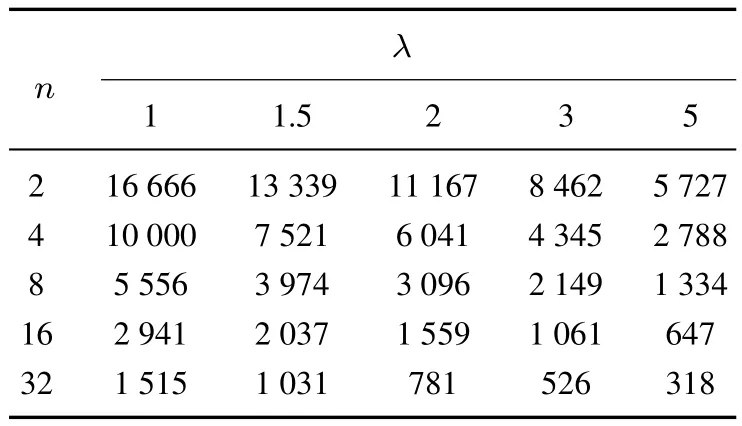
表2 批发价格契约下，不同损失厌恶系数λ、零部件种类数n所对应的组装商的最优订货量q∗Table 2 Optimal order quantities q∗with different loss-aversion coefficients λ and numbers of components n under a wholesale price contract

表2给出了批发价格契约下，不同损失厌恶系数λ、零部件种类数n所对应的组装商的最优订货量q∗.由表2可知：1）当组装商损失厌恶系数λ一定时，零部件种类数n越多，组装商的最优订货量q∗越低；并且当组装商损失厌恶系数λ分别为1、1.5、2、3、5时，随着零部件种类数n由2增加到32，组装商的最优订货量q∗分别减少了90.91%、92.30%、93.01%、93.80%、94.47%，这表明随着组装商损失厌恶系数λ的增加，零部件种类数n对组装商的最优订货量q∗的影响程度增大.2）当零部件种类数n一定时，组装商损失厌恶系数λ越大，组装商的最优订货量q∗越低；并且当零部件种类数n分别为2、4、8、16、32时，随着组装商损失厌恶系数λ由1增加到5，组装商的最优订货量q∗分别减少了65.64%、72.12%、75.99%、78.00%、79.01%，这表明随着零部件种类数n的增加，组装商损失厌恶系数λ对其自身最优订货量q∗的影响程度增大.

将表1、表2中的W∗以及q∗分别代入式（10）、式（14）可得到批发价格契约下组装商的期望效用）以及供应商的期望总利润.令，得到价格补贴契约下，零部件最优总批发价格∗（对于供应商而言），结合θ∗的取值，可以求得价格补贴契约下供应商的期望总利润，见表3.

表3 批发价格契约与价格补贴契约下供应商的期望

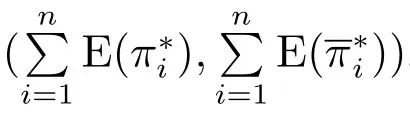
6 结束语

本文构建了由多个风险中性零部件供应商和单个损失厌恶组装商构成的组装供应链模型，分别对批发价格契约下各节点企业的最优策略以及协调契约的设计进行了研究.研究发现，在批发价格契约下，各节点企业的最优策略与零部件种类数以及组装商损失厌恶系数有关，并且组装商的最优订货量偏离了集中化情形下的最优订货量.通过数值分析进一步发现：当组装商损失厌恶系数一定时，零部件最优总批发价格与零部件种类数正相关，而组装商的最优订货量与零部件种类数负相关，并且随着组装商损失厌恶系数的增加，零部件种类数对零部件最优总批发价格以及组装商的最优订货量的影响程度都增大；当零部件种类数一定时，零部件最优总批发价格以及组装商的最优订货量都与组装商损失厌恶系数负相关；随着零部件种类数的增加，组装商损失厌恶系数对零部件最优总批发价格的影响程度减小，而对其自身最优订货量的影响程度增大.随后，文章着重分析了供应商如何使用价格补贴契约使组装商的最优订货量与集中化情形下的最优订货量一致，从而实现组装供应链协调.

［1］Fisher M，Raman A.Reducing the cost of demand uncertainty through accurate response to early sales.Operations Research，1996，44（1）：87—99.

［2］Schweitzer M E，Cachon G P.Decision bias in the newsvendor problem with a known demand distribution：Experimental evidence. Management Science，2000，46（3）：404—420.

［3］Wang C X，Webster S.Channel coordination for a supply chain with a risk-neutral manufacturer and a loss-averse retailer.Decision Sciences，2007，38（3）：361—389.

［4］Gan X H，Sethi S P，Yan H M.Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer.Production and Operations Management，2005，14（1）：80—89.

［5］Choi T M，Li D，Yan H.Mean-variance analysis of a single supplier and retailer supply chain under a returns policy.European Journal of Operational Research，2008，184（1）：356—376.

［6］闻 卉，曹晓刚，黎继子.基于CVaR的供应链回购策略优化与协调研究.系统工程学报，2013，28（2）：211—217. Wen H，Cao X G，Li J Z.Research on buy-back policy optimization and coordination of closed-loop supply chain based on CVaR. Journal of Systems Engineering，2013，28（2）：211—217.（in Chinese）

［7］史成东，陈菊红.Downside-Risk测度下三层供应链协调契约研究.中国管理科学，2010，18（1）：90—94. Shi C D，Chen J H.On three echelon supply chain coordination contract under the downside-risk measurement.Chinese Journal of Management Science，2010，18（1）：90—94.（in Chinese）

［8］李绩才，周永务，肖 丹，等.考虑损失厌恶一对多型供应链的收益共享契约.管理科学学报，2013，16（2）：71—82. Li J C，Zhou Y W，Xiao D，et al.Revenue-sharing contract in supply chains with single supplier and multiple loss-averse retailers. Journal of Management Sciences in China，2013，16（2）：71—82.（in Chinese）

［9］Chen X，Shum S，Simchi-Levi D.Stable and coordinating contracts for a supply chain with multiple risk-averse suppliers.Production and Operations Management，2014，23（3）：379-392.

［10］Leng M，Parlar M.Game-theoretic analyses of decentralized assembly supply chain：Non-cooperative equilibria vs.coordination with cost-sharing contracts.European Journal of Operational Research，2010，204（1）：96—104.

［11］Granot D，Yin S.Competition and cooperation in decentralized push and pull assembly systems.Management Science，2008，54（4）：733—747.

［12］Nagarajan M，SoiG.Coalition stability in assembly models.Operations Research，2009，57（1）：131—145.

［14］Yin S.Alliance formation among perfectly complementary suppliers in a price-sensitive assembly system.Manufacturing&Service Operations Management，2010，12（3）：527—544.

［15］Fang X.Capacity games for partially complementary products under multivariate random demands.Naval Research Logistics，2012，59（2）：146—159.

［16］Kalkancı B，Erhun F.Pricing games and impact of private demand information in decentralized assembly systems.Operations Research，2012，60（5）：1142—1156.

［17］罗定提，仲伟俊，梁美华.合作定价对装配式供应链运作效益影响的研究.系统工程学报，2002，17（4）：374—378. Luo D T，Zhong W J，Liang M H.Research on operation results effect of assemble-type supply chain through cooperative pricing. Journal of Systems Engineering，2002，17（4）：374—378.（in Chinese）

［18］Du D，Chen B，Xu D.Quantifying the efficiency of price-only contracts in push supply chains over demand distributions of known supports.Omega：The International Journal of Management Science，2014，42（1）：98—108.

［19］Gerchak Y，Wang Y.Revenue-sharing vs.wholesale-price contracts in assembly systems with random demand.Production and Operations Management，2004，13（1）：23—33.

［20］Gurnani H，Gerchak Y.Coordination in decentralized assembly systems with uncertain component yields.European Journal of Operational Research，2007，176（3）：1559—1576.

［21］Yang D，Choi T，Xiao T，et al.Coordinating a two-supplier and one-retailer supply chain with forecast updating.Automatica，2011，47（7）：1317—1329.

［22］付 红，马永开，唐小我.供应商损失厌恶情形下组装供应链协调.控制与决策，2013，28（10）：1465—1472. Fu H，Ma Y K，Tang X W.Coordination of assembly supply chain with loss-averse suppliers.Control and Decision，2013，28（10）：1465—1472.（in Chinese）

［23］Sarker B R，Fitzsimmons J A.The performance of push and pull systems：A simulation and comparative study.International Journal of Production Research，1989，27（10）：1715—1731.

［24］Lariviere M A，Porteus E L.Selling to the newsvendoran analysis of price-only contracts.Manufacturing&Service Operations Management，2001，3（4）：293—305.（in Chinese）

［25］卜祥智，赵泉午，黄 庆，等.易逝商品最优广告投入与订货策略的博弈分析.系统工程理论与实践，2004，24（11）：100—105. Bu X Z，Zhao Q W，Huang Q，et al.Game analysis of optimal advertising investment and order policy for perishable goods.Systems Engineering：Theory&Practice，2004，24（11）：100—105.（in Chinese）

［26］郭文革，陈 珽.信息不完全下的组合仲裁.自动化学报，1998，24（1）：56—63. Guo W G，Chen T.Combined arbitraiton with incomplete information.Acta Automatica Sinica，1998，24（1）：56—63.（in Chinese）

附录

引理1的证明 由式（15）对E（πi）求q的一阶导数得

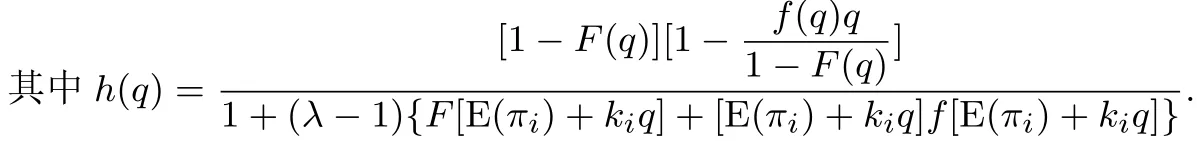
定理1的证明 由式（14）对E（πi）求wi的一阶导数，得

对式（17）两边求和，得

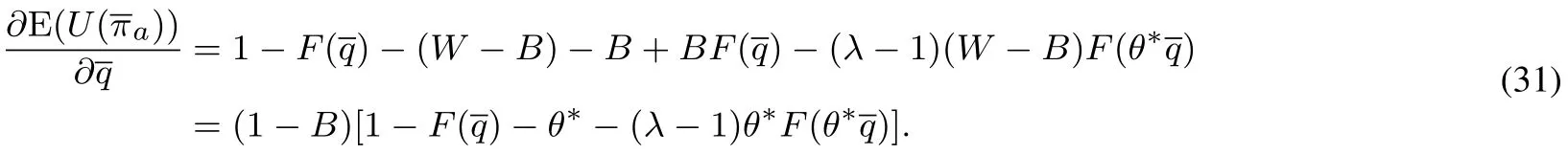
Coordination of assembly supply chain with a loss-averse assembler

Fu Hong，Ma Yongkai∗，Tang Xiaowo
（School of Management and Economics，University of Electronic Science and Technology of China，Chengdu 611731，China）

This paper investigates an assembly supply chain consisting of multiple risk-neutral suppliers and a loss-averse assembler.Firstly，the paper derives the equilibrium strategy of each enterprise under a wholesale price contract and shows that the assembler's optimal order quantity is less than that of a centralized system. Moreover，the numerical analysis shows that，for a given number of components，the assembler's optimal order quantity decreases in its loss-aversion coefficient，and the impact of the assembler's loss-aversion coefficient on its optimal order quantity increases.For a given assembler's loss-aversion coefficient，the assembler's optimal order quantity decreases in the number of the components，and the impact of the components' number on the assembler's optimal order quantity increases.Then，a coordination contract is designed by introducing the price-subsidy policy.The effectiveness of the coordination contract is verified by a numerical analysis.

assembly supply chain；loss-aversion；price-subsidy；coordination

F273

A

1000-5781（2016）04-0504-11

10.13383/j.cnki.jse.2016.04.008

付 红（1986—），男，安徽六安人，博士生，研究方向：供应链管理，Email：hongfu@uestc.edu.cn；

马永开（1963—），男，安徽天长人，博士，教授，博士生导师，研究方向：供应链管理，资本市场，Email：mayongkai@uestc.edu.cn；

唐小我（1955—），男，四川彭州人，博士，教授，博士生导师，研究方向：管理经济学，供应链管理，Email：xwtang@uestc.edu.cn.

2014-02-27；

2014-09-11.

国家自然科学基金资助重点项目（71531003）；国家自然科学基金资助项目（71101019）；教育部人文社科资助项目（12YJA630174）.

*通讯作者