不对称信息下弱势批发商与供应商的讨价还价问题研究

周继祥，王 勇

（重庆大学经济与工商管理学院，重庆400030）

不对称信息下弱势批发商与供应商的讨价还价问题研究

周继祥，王 勇

（重庆大学经济与工商管理学院，重庆400030）

研究了一个强势的供应商和一个弱势的批发商在最优生产量和最优订货量方面的讨价还价问题.建立了完全信息和不对称信息下批发商与供应商的讨价还价模型，得到了上述两种情况下批发商的讨价还价最优解，并据此给出了讨价还价最优解下批发商应给予供应商的最少支付以及批发商的信息价值.通过数值分析讨论了完全信息下一些重要参数对批发商的最优决策，最小成本和给予供应商的最小支付的影响，以及不对称信息下对批发商最优方案设计的影响.进一步的研究发现，弱势的批发商通过讨价还价可以减少成本和实现供应链协调.

供应链管理；最优策略；讨价还价；不对称信息

1 引 言

随着市场化程度越来越高，企业面临的竞争环境越来越激烈，降低库存成本成为企业十分关注的问题.然而，在库存管理中，库存成本最小这一目标时常会受到合作企业或竞争企业的掣肘而不能达到.以含有一个批发商，一个供应商的供应链为例.各自独立决策时，在确定性的环境下，他们会利用经济订购批量（EOQ）公式或经济批量（ELS）公式来制定最优策略.然而，在现实中，批发商的最优订货量与供应商的最优生产量在绝大多数情况下是不一致的.也就是说，批发商基于EOQ公式得到的最优解不能够被供应商所接受；类似的，供应商基于ELS公式得到的最优解也不能够被批发商所接受［1］.在这种情况下，势必至少有一方不能实现自身库存成本的最小化.发生上述情况时，供应商与批发商需要进行协调或讨价还价.

学者已经对供应链协调做了大量的研究，例如竞争环境下上游企业创新投入的协调，生鲜农产品的供应链协调，短生命周期产品定价协调，折扣诱导合同的协调，收益依赖下的收益共享协调，需求中断下的供应链协调，双渠道供应链的协调等［2-8］.然而，他们没有考虑这么一个现实问题，供应链中的供应商与批发商有着各自的市场势力.在有些供应链中，供应商比较强势，如苹果，三星，联想等；在另外一些供应链中，批发商则比较强势，如沃尔玛，苏宁，国美等.

而具有不同市场势力的企业在协商或者讨价还价过程中所处的地位是不同的，这一现象也引起了大批学者的关注.Netessine等［9］探讨了直销形式下不同势力结构对收益的影响.Bichescu等［10，11］在分散决策下研究了市场势力对供应链绩效的影响.Pan等［12］检查了包含有两个供应商，一个批发商或一个供应商，两个批发商的情形下，渠道势力是如何影响合同类型（收益共享合同VS批发价格合同）的选择的.Hua等［13］研究了在双渠道环境中，强势制造商的服务水平对均衡价格，制造商的利润以及批发商的利润的影响.Dan等［14］等在Hua的基础上研究了在双渠道环境中，弱势批发商的服务水平对均衡价格等的影响.Wu等［15］研究了不确定情况下的竞争性供应链的协调问题.Wu［16］研究了两个竞争性供应链讨价还价问题. Kwak等［17］刻画了一个供应商与一个批发商在长期补货合同上的讨价还价过程.汪峻萍等［18］建立了由单制造商单销售商组成的供应链协调及最优价格折扣模型，分别制定了对称信息与不对称信息两种情形下供应链协调机制.艾兴政等［19］对不同讨价还价能力和产品差异的竞争渠道结构的演化过程进行了分析.陈敬贤等［20］考虑了顾客退货情况下零售商之间的博弈问题.夏海洋等［21］考察了供应商的供货中含有瑕疵品，且零售商压缩订购费用情况下的订货批量模型.文献［9—21］都是使用Stackelberg模型来刻画供应商与批发商的市场地位，而且，他们都是使用集中决策来描述供应链的协调.而在现实中，供应商与批发商都是独立的企业，强势企业无法决定弱势企业的决策.因此，许多学者使用了其它的方法来刻画供应链中供应商，批发商的市场势力问题.如，王小龙等［22］使用一类契约来反映零售商的强势，王圣东［23］认为在供应商弱势的情况下，他可以选择与多个批发商合作来达到减少成本的目的.Sucky［24］使用讨价还价模型研究了一个强势批发商与一个弱势供应商的协调问题.在他的研究中，供应商使用“批量流”的决策方式决策，然而他没有给出弱势企业向强势企业的支付，而且他只考虑了完全信息的情况.

在上述文献的研究中，强势企业的市场势力主要体现在优先决策上.本文认为，不管强势企业是否优先决策，他都必须保证自己改变策略后的成本不高于自己单独决策下的成本，只有这样他才可能跟弱势企业合作.因此，弱势企业可以通过给予强势企业一些补偿的方式来达到使强势企业改变策略，减少自身成本的目的.鉴于此，本文从弱势企业的角度出发，在Banerjee［25］的研究基础上研究了一个强势供应商和一个弱势批发商在最优决策方面的讨价还价问题，并分别讨论了完全信息与不对称信息下批发商与供应商的讨价还价最优解以及批发商应给予供应商的最低支付.

2 联合经济批量模型中的采购与生产策略

本节以联合经济批量模型为基础，讨论了一个独立决策的批发商与一个独立决策的供应商的最优订购量与最优生产量问题.为使模型简单，易于理解，做如下基本假设：

1）批发商与供应商都是风险中性的，在本文中，他们都以自己的单位周期的成本最小为目标；

2）产品需求是确定的；

3）缺货费用无穷大，即，不允许缺货；

4）需求是连续的，均匀的；

5）当存储降至零时，可以立即得到补充；

6）每次订货量以及订货费用不变；

7）批发商与供应商的单位存储费用不变.

符号说明：

xA为批发商的每次订货量，决策变量；

d为产品的需求率；

hA为批发商对单位产品的库存成本；

B为批发商的每次订购费用；

KA（xA）为批发商在单个周期的成本，包括产品的库存成本和订货成本；

xP为供应商的每次生产量，决策变量；

p为供应商的生产率，p＞d；

hp为供应商对单位产品的库存成本；

R为供应商的生产准备成本；

KP（xP）为供应商在单个周期的成本，包括产品的库存成本和生产准备成本.

2.1 个人最优策略

根据Banerjee［25］的研究，在自身成本最小化的目标下，批发商或供应商会使用经济订货批量模型（EOQ模型）来决策订货量或生产量.

批发商的目标是制定一个最优订货策略来使得他在单个周期内总成本最小.批发商的总成本为

供应商的目标是制定一个最优生产策略来使得他在单个周期内的成本最小.供应商的总成本为

2.2 整合下的联合订货与生产策略

如果供应商采取“批对批”法，则供应商的生产量等于运送给批发商的产品数量，批发商的订货量等于供应商运送给他的产品数量.由于不存在缺货现象，有联合订货与生产量xG=xA=xP.因此，批发商与供应商的总成本为

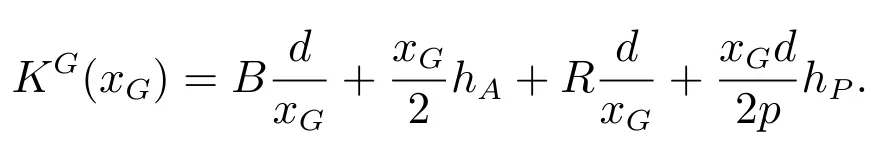
2.3 个人策略与联合策略的对比

对于任意的联合批量xG，供应商的准备成本和批发商的订购成本的关系，以及供应商和批发商的库存成本之间的关系可用α和β表示如下

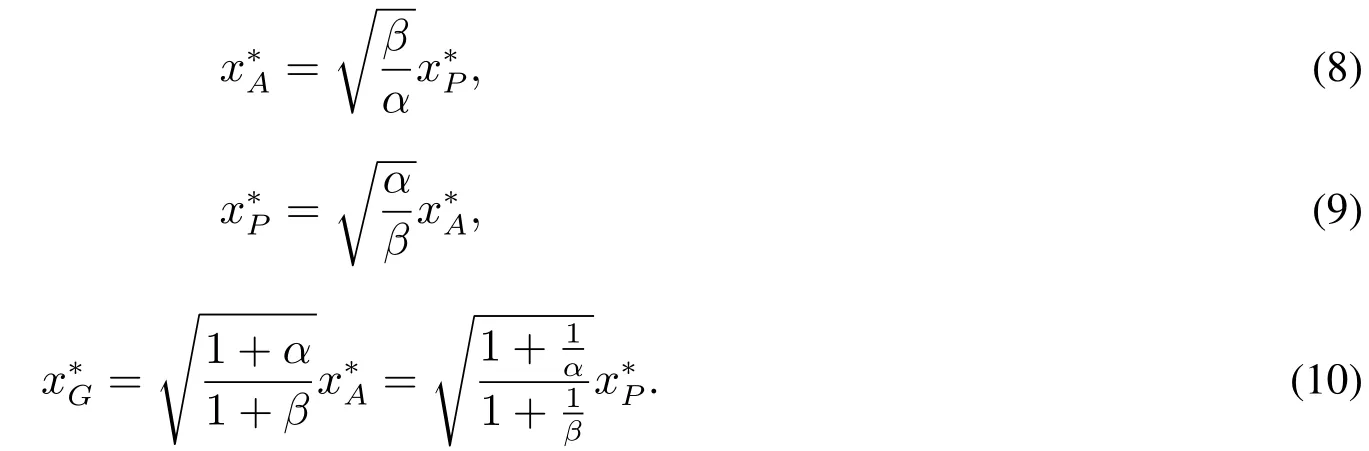
由式（8），式（9），式（10）可知，当且仅当α=β时，.而更多情况下α≠β，此时联合订购批量介于最优生产量与最优订货量之间.即，当时］；当时.要想在α≠β的情况下三者相等，要么批发商足够强势，此时有；要么供应商足够强势，此时有；要么批发商和供应商都改变自身最优决策，此时有

表1 个人替代策略的结果Table 1 The consequences of individual alternative policies

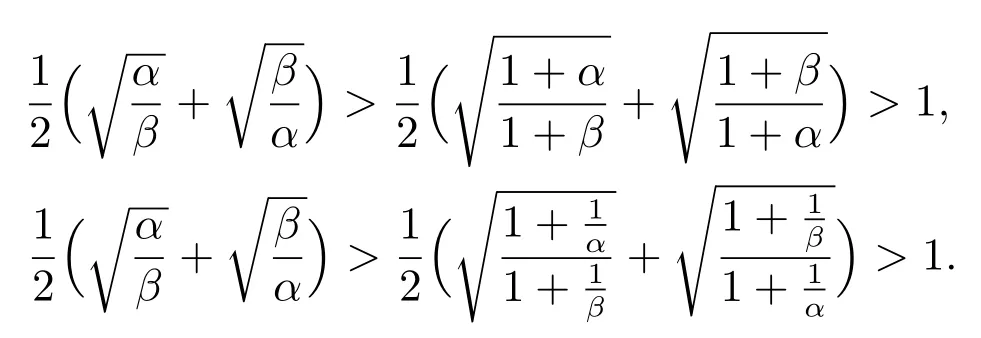
由以上分析，可得如下命题

命题1任何偏离个人最优策略的行为都会导致自身成本的增加.

命题2采用对方的最优策略导致的成本增加量大于采用联合最优策略导致的成本增加量.

由命题1可知，在合作中，一个理性的批发商（供应商）没有偏离自身最优策略的动机.因此，在α≠β的情况下，双方只有通过一系列的协商才能使得联合策略xG=xA=xP.由命题2可知，双方通过协商来降低总成本是可行的.例，当强势的供应商要求批发商按照供应商的最优策略订货时，批发商可以给予供应商一定的补偿来促使供应商选择其他的生产策略，如联合最优策略.

3 完全信息下的讨价还价模型

3.1 讨价还价模型

如果批发商和供应商都是理性的，他们将会选择自己的最优策略和.如果供应商（批发商）有足够的市场话语权，他会利用这个权利让批发商（供应商）执行自己的最优策略.此时，弱势的企业就只能执行强势企业的最优策略.然而，当双方可以协商时，弱势企业就会通过支付给强势企业一定的费用来达到让强势企业改变个人最优策略的目的.本文将试图找出在供应商和批发商可以协商的情况下他们将会制定怎么样的联合策略.用（N,U,u∗）表示供应商与批发商的讨价还价博弈.其中N=｛（A）,（P）｝表示参与人集合，U是供应商与批发商成本组合的集合，u∈U，威胁点u∗∈U在谈判破裂的情况下得到实现.基于讨价还价问题的现实性，所有的参与人至少存在一个成本组合,i∈N；至少对一个参与人有,i∈N.讨价还价模型描述如下

1）供应商具有足够的市场话语权来执行自己的最优生产策略，即，在谈判破裂时有.威胁点u∗可表示为

2）如果批发商想要供应商改变个人最优策略，那么批发商支付给供应商的费用必须不小于供应商由此引起的成本增加量.假设批发商支付给供应商的费用为z，此时批发商提出的联合策略为xG，则可行的成本组合为u=（KA（xG）+z,KP（xG）+z）,xG＞0,z≥0.

3）在博弈过程中，批发商首先给出报价，一旦供应商接受或拒绝这个报价，博弈马上结束. 4）博弈过程中没有交易成本，且批发商对供应商的成本函数具有完全信息.

3.2 完全信息下的讨价还价解

本小节将对批发商提出的联合策略进行分析，并讨论批发商给予供应商的最低补偿.由于供应商具有市场话语权，他可以独自制定最优策略.因此，在没有协商的情况下联合批量，此时

对于批发商来说，在满足约束条件的前提下z越小越好.由式（12）可知，当z=KP（xG）-KP时z有最小值.将z=KP（xG）-KP代入式（11），则原问题转化为求解的最小值问题.将式（1），式（3）代入目标，利用均值不等式，则有

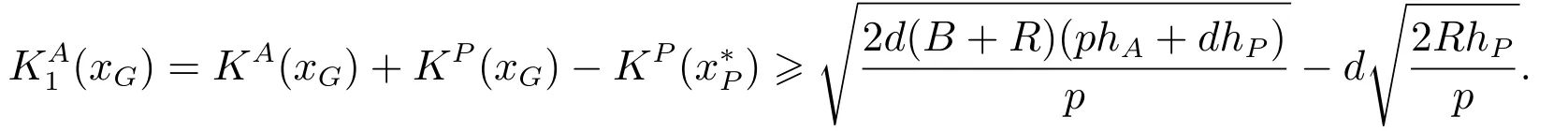
命题3完全信息下，批发商提出的联合最优策略及给予供应商的最低支付如下

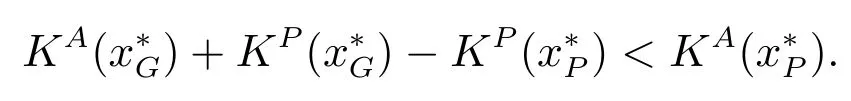
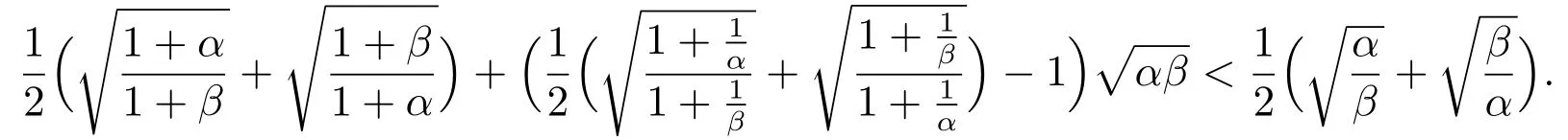
容易证明，对任意的α≠β，且α,β＞0，上式成立.因此，有如下命题.

命题4完全信息下，供应商和批发商可以达成协调，且批发商可以从讨价还价中获得讨价还价盈余

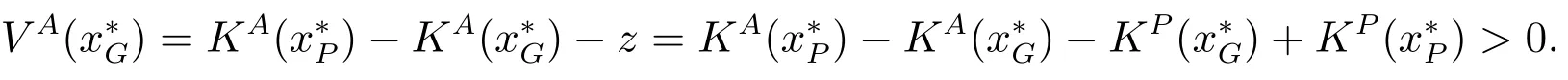
4 不对称信息下的讨价还价模型

4.1 不对称信息下讨价还价的情形

4.2 不对称信息下讨价还价模型

假设供应商有（P1），（P2）两种成本结构，两种成本结构下的成本函数分别为和.供应商的成本结构为（P1）的概率为ω1，在此成本结构下，供应商的库存成本为hP1，生产准备成本为R1.供应商的成本结构为（P2）的概率为ω2=1-ω1，在此成本结构下，供应商的库存成本为hP2̸=hP1，生产准备成本为R2.假设批发商提供的方案集为（x1,z1,x2,z2），其中x1是供应商的成本结构为（P1）时的联合策略，z1为此时的补偿；x2是供应商的成本结构为（P2）时的联合策略，z2为此时的补偿.如果批发商不这么做，且当供应商的成本结构为（P2）时批发商仅提供了针对成本结构为P1时的方案.此时，成本结构为（P2）的供应商可能对批发商宣称自己的成本结构为（P1），并借此获得的利润.为了避免这种情况的发生，批发商不得不提供联合策略x1,x2以及对应的补偿z1,z2来保证不同类型的供应商必须接受针对他的真实成本结构类型设计的方案.此时，问题转化为求解如下非线性规划

不等式（14），式（15）是个人理性约束，保证了供应商会接受批发商的提议.不等式（16），式（17）是激励相容约束，保证了供应商没有隐瞒自己真实成本结构的动机.供应商的成本函数KP（x1），KP（x2），以及批发商的成本函数KA（x1）分别是x1，x2，x1的严格凸函数.因此，满足KKT条件（Karush-Kuhn-Tucker conditions）的解即为原问题的最优解.通过对KKT条件进行分析，可以得到满足条件（14）～（18）的六个可行方案，由成本函数的凸性可知这六个可行方案也是目标函数（13）的最优方案，证明略.

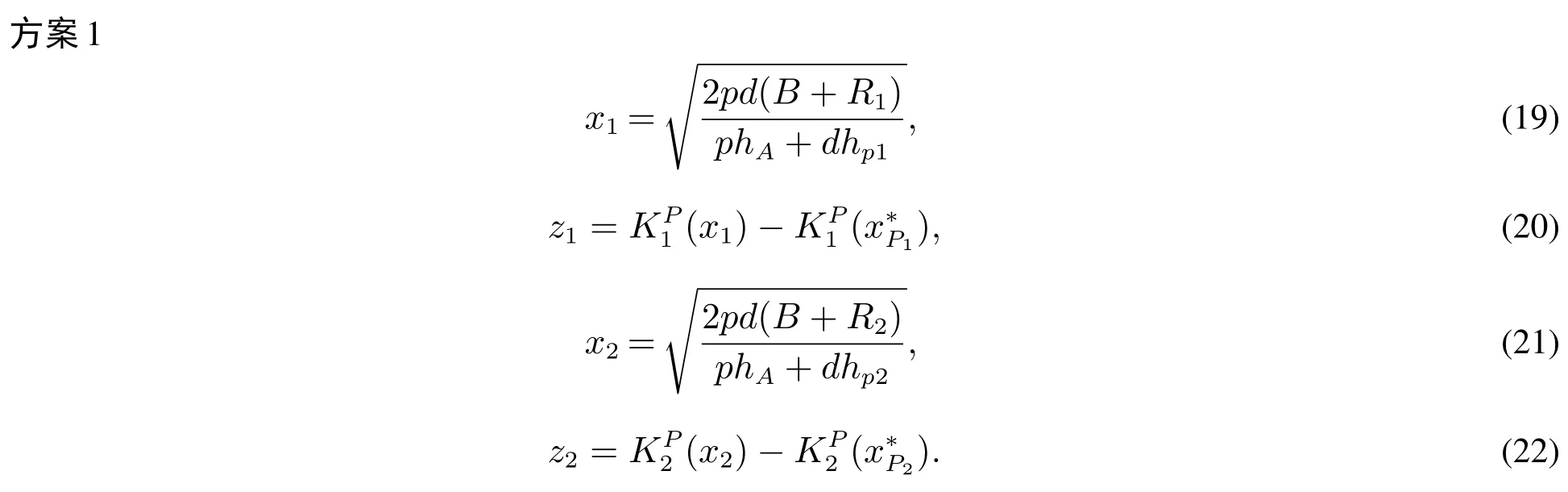
可以看到，方案1跟完全信息下讨价还价的联合最优策略是一致的.此时，批发商给予供应商的补偿z1，z2也恰好分别等于供应商从产量转为x1，从产量转为x2增加的成本.如果供应商有动机选择不是为他的真实成本结构而设计的合同，那么方案1就不是最优的.考虑下面这两情况：1，供应商的真实成本函数是，但是供应商有动机接受基于成本函数设计的合同；2，供应商的真实成本函数是，但是供应商有动机接受基于成本函数设计的合同.在这两种情况下，供应商都会为了得到或者的利润而隐瞒自己的成本结构.方案2～方案6的设计避免了上述情形的发生.

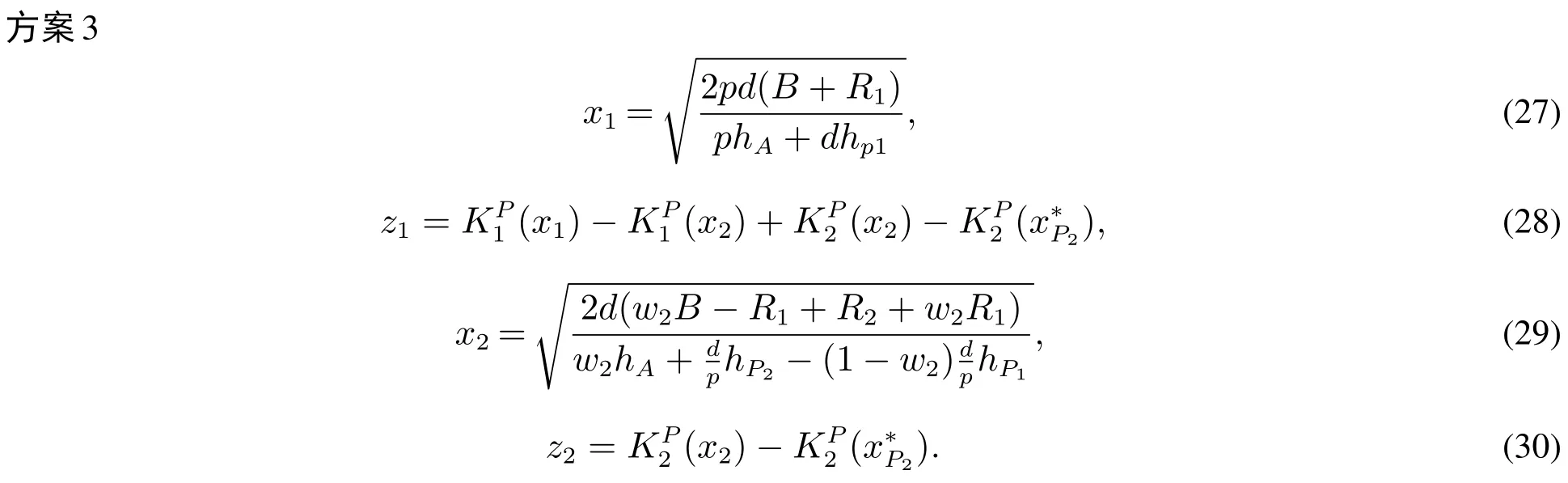
方案3的设计目标与方案2正好相反，方案3是为下列情形设计的：供应商的成本函数是（x），然而他却有动机接受基于成本函数（x）设计的方案.从（x）的角度来看，一方面，批发商通过提供一个不太有吸引力的x2（不是由联合批量模型确定的联合最优策略，方案1中的x1,x2是由联合批量模型确定的联合最优策略）来避免供应商隐瞒其（P1）类型的成本结构.另一方面，批发商给予供应商的费用z1不仅包括了供应商将产量从转向产量x1时增加的成本，还包括了一个供应商不隐瞒其真实成本结构（P1）的奖励.

在本方案中，批发商提供了一个不太吸引人的策略x2来防止本来成本结构为（P1）的供应商隐瞒自身成本结构.另外，由于供应商两种情况下的成本结构不同，再针对式（33），给出一个合理的假设hP1̸=hP2.

在本方案中，批发商提供了一个不太吸引人的策略x1来防止本来成本结构为（P2）的供应商隐瞒自身成本结构.

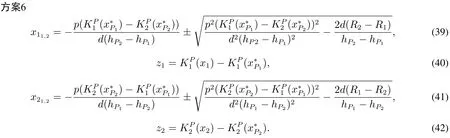
方案6是为一种特殊的情形设计的，在这种情形下，当供应商的成本函数为（x）时，他有动机接受批发商针对他的成本函数为（x）设计的策略；供应商的成本函数为（x）时，他有动机接受批发商针对他的成本函数为（x）设计的策略.而在本方案下，如果供应商是理性的，他会根据自身的成本结构选择批发商按照他的相应成本函数设计的策略.

从信息经济学的角度来看，市场信息的不完全性与不对称性使得信息具有了价值，也使得信息能够作为一种特殊的商品而存在.通过以上分析发现，在完全信息与不对称信息下批发商的最小总成本是不同的，因此，信息是有价值的.对于本文中的批发商来说，信息的价值就是批发商在完全信息与不对称信息下的成本之差.因此，有如下命题

命题5在完全信息与不对称信息下，批发商的信息价值如下

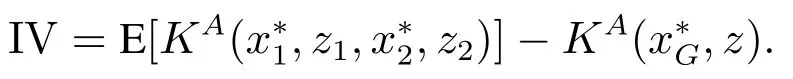
由命题5，式（11），式（13）以及批发商给予供应商的补偿z的表达式可知，影响批发商信息价值的因素主要包括供应商和批发商的成本结构以及批发商在不对称信息下对供应商成本结构估计的概率.

5 数值分析

为了进一步说明本文讨价还价模型的有效性和探讨外生变量对供应商，批发商以及供应链系统的影响，本节将通过算例分别对完全信息以及不对称信息下的讨价还价模型进行分析，并对两种情况下的结论进行比较.

5.1 完全信息的情况

假设d=10 000,p=15 000,B=100,R=135,hA=50,hP=45.将上述参数代入相关公式，通过Matlab软件计算可得表2.

表2 数值实验1Table 2 Numerical experiment 1

观察表2，可得以下结论：

2）由表2最后三列可以发现，对任意的d,B,hA,p,R,hP，有成立.即，供应商因改变个人最优策略而引起的成本上升可由批发商的支付完全补偿.因此，供应商选择个人最优策略与联合最优策略是无差异的.而且，供应商选择联合最优策略可使得供应链系统的总成本降低.因此，供应商有改变个人最优策略的动机.综上，批发商与供应商可以实现协调.

3）对批发商来说，单位库存成本hA的变化对其总成本的影响最大.同时，批发商的单位库存成本对其给予供应商的支付也有着极大的影响.由表2可以发现，当hA增加20%时，批发商的总成本以及给予供应商的支付分别增加11.3%和63.4%；当hA减少20%时，批发商的总成本以及给予供应商的支付分别增加12.0%和52.7%.因此，批发商应致力于减少单位库存成本.

4）对供应商来说，对其影响最大的是产品的需求率.从供应商的成本函数可以发现，产品的需求率不仅影响着库存成本，而且极大的影响着准备成本.而从自身来说，供应商的生产率，库存成本以及准备成本都对其总成本有较大的影响.因此，供应商应大力提高生产率，降低单位库存成本以及准备成本来提高竞争力.

5）对供应链系统来说，产品需求率的变化对系统总成本的影响最大.由表2可知，当d增加20%时，供应链系统的总成本提高13.6%；当d减少20%时，供应链系统的总成本降低14.0%.从系统总成本的公式可以发现，这是由于d是唯一一个既影响供应商总成本又极大地影响着批发商总成本的因素.

5.2 不对称信息的情况

在其他条件不变的情况下，分析d,B,hA,p对供应商，批发商以及系统成本的影响可得到与完全信息下相同的结论；分析R1，hP1或R2，hP2也可得到与完全信息下分析R,hP相同的结论.由于供应商具有市场话语权，不管w1,w2如何变化，供应商的期望成本不变（此时批发商给予供应商的补偿最少且供应商有动机接受批发商的联合最优策略）.因此，下面将着重分析w1,w2对批发商和系统的影响以及其它参数的变化对批发商最优方案的影响.假设d=10 000,p=15 000,B=100,hA=50,R1=135,R2=180,hP1=45,hP2=33.75.通过Matlab软件计算可得表3.观察表3，可得以下结论：

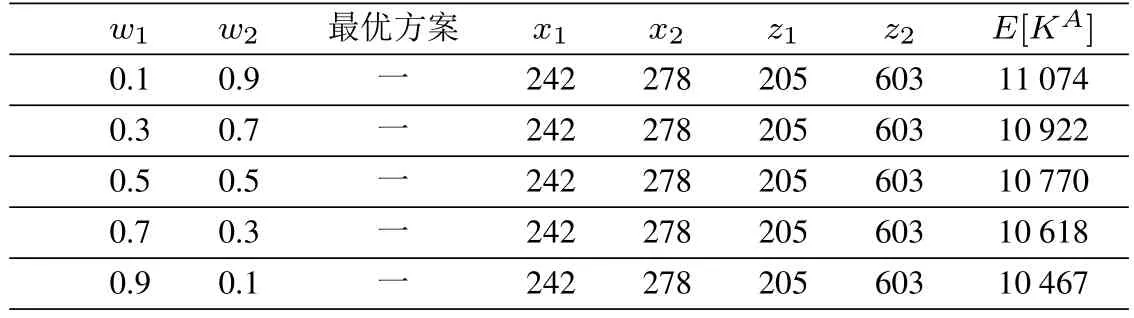
表3 数值实验2Table 3 Numerical experiment 2

1）不管w1，w2如何变化，批发商的最优方案，供应商成本结构既定情况下的联合最优订货量以及批发商给予供应商的补偿不变，即x1,x2,z1,z2不变.因此，可以认为批发商和供应商的成本结构，w1和w2对批发商的期望成本有重大影响.例，由于在联合最优订货量既定的情况下，批发商在x2=278时的成本较大以及在这种情况下批发商给予供应商的补偿较大，使得批发商的期望成本随着w1的增加（或w2的减少）而降低.因此，在得知w1,w2对批发商期望成本有重大影响时，批发商会在准确估计供应商的成本结构方面加大投入.

2）当不存在协商时，批发商的期望总成本E（x1=300,z1=0,x2=400,z2=0）=11 667，大于任一协商情况下批发商的期望总成本，且协商情况下供应商的成本没有增加.因此，在不对称信息下批发商与供应商可以实现协调.

通过进一步的数值分析可知，影响批发商最优方案选择的是批发商以及供应商的成本函数.例如，在其它情况不变的情况下，当d=4 000或p=150 000时，批发商将会选择方案2；当B=10 000时，批发商将会选择方案3.当R2=1.8×1023且hP2=3.375×1020时，方案5才会以微弱的优势胜出.而现实中供应商的准备成本以及库存成本不可能如此大，因此，可以认为批发商不会选择方案5.方案4以及方案6与方案5有类似的问题.因此，批发商在实际准备方案时将会只考虑方案1，方案2，方案3.

图1给出了本小节参数假设信息下的（P1），（P2）成本结构的供应商以及批发商的成本函数，各自的最优策略以及联合最优策略x1,x2.

图1 不同类型的供应商下的最优联合策略Fig.1 Joint optimal policies for different assumed types of（P）

5.3 完全信息与不对称信息下讨价还价模型的比较

对比完全信息以及不对称信息下的讨价还价模型，可得以下结论：

1）不管在完全信息还是不对称信息下，供应商与批发商均可实现协调.

2）在其它条件不变的情况下，当外生变量发生小幅波动（如20%）时，在两种情况下，外生变量的变化对于供应商，批发商以及系统的影响相同.然而，当外生变量变化巨大（如，当d从10 000减少到4 000）时，在完全信息下的影响仅仅表现为联合最优决策的变化，供应商和批发商以及系统成本的变化；而在不对称信息下，除了上述变化外更有批发商最优方案设计的改变.

3）信息的重要性.在完全信息下，批发商知道供应商的全部信息，他拥有唯一的方案使得供应商成本最小的同时自己的总成本最小；而在不对称信息下，他必须制定多个方案以防止供应商撒谎，同时他只能保证自身的期望总成本最小.

6 结束语

本文研究了一个强势的供应商与一个弱势的批发商的讨价还价问题.通过上述分析可知，对于整个系统来说，联合最优决策总是最省钱的.然而，当联合最优策略跟强势企业的最优策略不同时，强势企业没有动机执行这一策略.相反，他会利用自身的市场优势来强迫弱势企业执行强势企业的策略.此时，弱势企业可以通过讨价还价来尽量减少自身的损失.为此，就不难理解企业需要做大做强的原因，也能够理解为什么一些企业想要并购上游或下游企业.通过数值分析可以发现，不管在完全信息还是不对称信息下，讨价还价的存在对供应商，批发商以及整个供应链系统来说都是有利的.在不对称信息下，批发商和供应商的成本函数以及供应商成本结构类型的概率对批发商的期望成本有重大影响，而且批发商以及供应商的成本函数还可进一步影响批发商最优方案的设计.可以说，如果批发商不知道供应商的具体成本函数，批发商就不能设计出最优方案，而且还有可能进一步影响讨价还价的可行性.本文的研究是在批发商面临确定需求的假设下进行的，然而现实中批发商面临的需求往往是随机的，不确定的，这一问题还有待进一步的研究.

［1］Sucky E.A bargaining model with asymmetric information for a single supplier-single buyer problem.European Journal of Operational Research，2006，171（2）：516—535.

［2］田 巍，张子刚，刘宁杰.零售商竞争环境下上游企业创新投入的供应链协调.系统工程理论与实践，2008，28（1）：64—70. Tian W，Zhang Z G，Liu N J.Study on supply chain coordination of upstream innovation investment when retailers compete.Systems Engineering：Theory&Practice，2008，28（1）：64—70.（in Chinese）

［3］但 斌，陈 军.基于价值损耗的生鲜农产品供应链协调.中国管理科学，2008，16（5）：42—49. Dan B，Chen J.Coordinating fresh agricultural supply chain under the valuable loss.Chinese Journal of Management Science，2008，16（5）：42—49.（in Chinese）

［4］黄 河，徐鸿雁，王 旭.短生命周期产品动态定价下供应链协调问题分析.重庆大学学报：自然科学版，2007，30（6）：150—154. Huang H，Xu H Y，Wang X.Supply chain coordination for perishable product with dynamic pricing policy.Journal of Chongqing University：Nutural Science Edition，2007，30（6）：150—154.（in Chinese）

［5］Saha S.Supply chain coordination through rebate induced contracts.Transportation Research：Part E，Logistics and Transportation Review，2013，50：120—137.

［6］Palsule-Desai O D.Supply chain coordination using revenue-dependent revenue sharing contracts.Omega：International Journal of Management Science，2013，41（4）：780—796.

［7］Qi X，Bard J F，Ye G.Supply chain coordination with demand disruptions.Omega：International Journal of Management Science，2004，32（4）：301—312.

［8］但 斌，徐广业.随机需求下双渠道供应链协调的收益共享契约.系统工程学报，2013，28（4）：514—521. Dan B，Xu G Y.Revenue sharing contract for dual-channel supply chain coordination with stochastic demand.Journal of Systems Engineering，2013，28（4）：514—521.（in Chinese）

［9］Netessine S，Rudi N.Supply chain structures on the internet and the role of marketing-operations interaction.International Series in Operations Research and Management Science，2004，74：607—641.

［10］Bichescu B，Fry M J.Channel power analysis under vendor-managed inventory and a general（Q，R）inventory policy.OR Spectrum，2009，31（1）：195—228.

［11］Bichescu B，Fry M J.A numberical analysis of supply chain performance under split decision rights.Omega：International Journal of Management Science，2009，37（2）：358—379.

［12］Pan K，Lai K K，Leung S C H，et al.Revenue-sharing versus wholesale price mechanisms under different channel power structures. European Journal of Operational Research，2010，203（2）：532—538.

［13］Hua G，Wang S，Cheng T C E.Price and lead time decisions in dual-channel supply chains.European Journal of Operational Research，2010，205（1）：113—126.

［14］Dan B，Xu G，Liu C.Pricing policies in a dual-channel supply chain with retail services.International Journal of Production Economics，2012，139（1）：312—320.

［15］Wu D，Baron O，Berman O.Bargaining in competing supply chains with uncertainty.European Journal of Operational Research，2009，197（2）：548—556.

［16］Wu D D.Bargaining in supply chain with price and promotional effort dependent demand.Mathematical and Computer Modelling，2013，58：1659—1669.

［17］Kwak T C，Kim J S，Moon C.Supplier-buyer models for the bargaining process over a long-termreplenishment contract.Computers Industrial Engineering，2006，51（2）：219—228.

［18］汪峻萍，王圣东.非对称信息下以制造商为核心的供应链协调模型.系统工程学报，2008，23（1）：60—66. Wang J P，Wang S D.A coordination model on the manufacturer core supply chain under asymmetric information.Journal of Systems Engineering，2008，23（1）：60—66.（in Chinese）

［19］艾兴政，唐小我.基于讨价还价能力的竞争供应链渠道结构绩效研究.管理工程学报，2007，21（2）：123—125，133. Ai X Z，Tang X W.Study about the performance of competing channel structure under bargaining power.Journal of Industrial Engineering and Engineering Management，2007，21（2）：123—125，133.（in Chinese）

［20］陈敬贤，王国华，梁 樑.顾客退货影响的多零售商库存博弈.系统工程学报，2013，28（1）：101—108. Chen J X，Wang G H，Liang L.Inventory game among multi retailers under customer returns' impact.Journal of Systems Engineering，2013，28（1）：101—108.（in Chinese）

［21］夏海洋，黄培清，范体军，等.考虑订购费用压缩下含瑕疵品的订货批量模型.系统工程学报，2012，27（4）：520—526. Xia H Y，Huang P Q，Fan T J，et al.Ordering quantity model with consideration of random defective rate and ordering cost reduction. Journal of System Engineering，2012，27（4）：520—526.（in Chinese）

［22］王小龙，刘丽文.下游零售商强势背景下的多对一供应链协调模型.中国管理科学，2008，16（5）：96—109. Wang X L，Liu L W.A multi-supplier single-retailer supply chain coordination model with the retailer being dominant.Chinese Journal of Management Science，2008，16（5）：96—109.（in Chinese）

［23］王圣东.单供货商多销售商联合生产库存模型.系统工程学报，2006，21（1）：92—96. Wang S D.Production inventory models for a one-vendor multi-buyer integrated system.Journal of Systems Engineering，2006，21（1）：92—96.（in Chinese）

［24］Sucky E.Inventory management in supply chains：A bargaining problem.Interational Journal of Production Economics，2005，93：253—262.

［25］Banerjee A.A joint economic-lot-size model for purchaser and vendor.Decision Sciences，1986，17（3）：292—311.

Research on a bargaining problem between a disadvantaged wholesaler and a supplier under asymmetric information

Zhou Jixiang，Wang Yong
（School of Economics and Business Administration，Chongqing University，Chongqing 400030，China）

This paper discussed a bargaining problem between an advantaged supplier and a disadvantaged wholesale in the case of optimal production quantity and optimal order quantity.Two bargaining models were established for the supplier and the wholesaler under the condition of complete information and asymmetric information.The optimal solution of bargaining for the wholesaler in the above two cases was attained.According to that，the least paying that the wholesaler should pay for the supplier and the information value of the wholesaler under the bargaining optimal solution were suggested.On the analysis of the values，the best decision of some important values for the wholesaler in complete information and the minimum cost and impacts of giving the supplier the minimum payments were discussed，as well as the impacts on the wholesaler's optimal design plan.Further the research found that the cost could be reduced for the disadvantaged wholesaler so as to achieve the coordination of supply chain by bargaining.

supply chain management；optimal strategy；bargaining；asymmetric information

F253.4

A

1000-5781（2016）04-0481-13

10.13383/j.cnki.jse.2016.04.006

周继祥（1986—），男，江苏徐州人，博士生，研究方向：物流管理，Email：zhoujixiang860904@163.com；

2013-08-05；

2014-06-05.

国家自然科学基金资助项目（71272085）；教育部人文社会科学研究规划基金资助项目（12YJA630135）.

王 勇（1957—），男，四川内江人，博士，教授，博士生导师，研究方向：优化方法，物流管理，Email：wangyongkt@163.com.