大跨度铁路钢桁连续梁桥抗震分析方法研究

杨华平，宋重阳，钱永久，黎璟，邵长江

（1.西南交通大学土木工程学院，四川成都610031；2.中交第二公路勘察设计研究院有限公司，湖北武汉430056）

大跨度铁路钢桁连续梁桥抗震分析方法研究

杨华平1，宋重阳2，钱永久1，黎璟1，邵长江1

（1.西南交通大学土木工程学院，四川成都610031；2.中交第二公路勘察设计研究院有限公司，湖北武汉430056）

采用非线性结构分析软件SAP2000建立了某全长504 m的3跨铁路钢桁连续梁桥有限元模型，研究了大跨度铁路钢桁梁连续梁桥的振动特性，并对此类桥梁地震响应分析方法进行了讨论。研究表明:与常规混凝土连续梁桥相比，大跨度铁路钢桁梁桥振型密集复杂，沿用常规混凝土铁路连续梁桥取较少振型组合进行反应谱计算，可能会导致结果精度不可接受。应用瑞利阻尼确定结构阻尼矩阵进行直接积分时程分析时，阻尼矩阵计算振型应选取计算方向参与质量大的前两阶振型，而通过快速非线性分析方法（FNA）设置常阻尼比0.05进行时程分析可得到略保守的计算结果。

抗震分析；钢桁连续梁桥；反应谱；时程分析；阻尼

随着我国基础建设事业的推进及沿海与内陆地区交通网络的不断完善，作为强震多发区域的西部山区公路、铁路建设已成为当前交通建设的重点。大跨度钢桁连续梁桥因上部结构质量较轻、跨越能力出色、便于抢修等突出优势，在不少强震区桥梁方案选型中获得了较为广泛的应用。如东新赣江铁路桥［1］，中宁黄河特大桥［2］等。

但由于大跨度钢桁连续梁桥振动特性和震害机理的特殊性，工程师对混凝土连续梁桥进行抗震计算时常使用的一些不至于导致过大误差的习惯设置，沿用到大跨度钢桁连续梁桥抗震分析却可能严重影响分析结果。

本文以一座全长504 m的3跨铁路钢桁连续梁特大桥为工程背景，讨论了纵向地震荷载激励下反应谱和时程计算分析时的计算要点。研究结论可为大跨度铁路钢桁连续梁桥抗震分析提供参考。

1　工程概况

某铁路特大桥为全长504m、跨径组合（140+224 +140）m、设计行车速度250km/h的双线客运专线桥梁，线间距4.6m。主桥钢桁梁采用N形桁架、两片主桁、桁宽14m，跨中桁高16m，支点桁高32m，节间长度14.0m。上、下弦杆均采用箱形截面，主桁腹杆采用箱形截面及H形截面。桥面采用纵横梁结构体系，每一线铁路下方设2道纵梁，间距2.0m，沿桥纵向每一节点处设1道横梁，纵梁全桥连续，遇横梁时与横梁栓焊连接。主桥17#，18#桥墩采用圆端形实体墩，墩顶纵、横向宽度分别为7，16.6m。原设计方案在17#桥墩上设置纵向固定支座，18#桥墩和边墩纵向均可活动，同时各主墩横向均设置固定支座。桥型布置见图1。

图1　桥型布置（单位：m）

2　结构振动特性及分析要点

2.1设计方案结构有限元模型

采用非线性结构分析软件SAP2000建立了该桥有限元分析模型，如图2所示。

模型中上部结构和下部结构都采用三维空间梁单元进行模拟，整个模型共1044个节点，2213个梁单元。固定与活动支座均采用弹性连接模拟，各自由度方向刚度值按是否约束取1×107kN/m和0。

2.2桥梁结构动力特性

采用子空间迭代法对该桥振动特性进行分析研究。分析结果表明，该桥振型密集复杂，且低阶振型多为上部结构自振，结构质量参与系数较低，前20阶振型纵向质量参与系数仅为58.5%。18#墩墩身自振出现在第22阶（纵桥向质量参与系数15.8%），振动周期为0.405 s，考虑第22阶振型后纵向质量参与系数提升到了74.3%。表1列出了该桥前5阶振型的振动形式及周期。

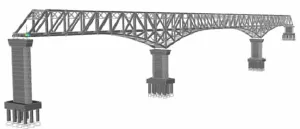
图2　有限元模型

表1　前5阶振型特性

2.3地震响应分析要点

2.3.1场地特性及分析用地震动时程

桥址处为7度区，场地特征周期为0.4 s。罕遇地震（50年超越概率2%）下设计地震峰值加速度为0.21g。依据铁路工程抗震设计规范，设计地震加速度放大系数β（T）表达式

式中：T，Tg分别为结构自振周期和场地特征周期。

根据铁路工程抗震设计规范，采用三角级数方法合成拟合3条反应谱与目标反应谱差值在5%以内的人工地震波用于分析。人工波加速度时程曲线见图3。

2.3.2反应谱计算分析要点

多自由度结构进行反应谱计算分析时，除确定场地反应谱外，计算振型数目及振型的组合是反应谱法中的两个基本问题。本桥振型密集复杂，为考虑振型频率接近时的耦合效应，振型的组合采用Wilson等［3］根据随机过程理论导出的振型组合规则CQC法，这也是当前我国公路和城市桥梁抗震规范［4-5］在进行大跨桥梁反应谱分析时推荐采用的方法。对于计算振型数目，我国公路和城市桥梁抗震规范要求计算方向的振型参与质量和超过90%，而我国铁路抗震规范未作出明确规定。在进行常规混凝土铁路连续梁桥进行反应谱分析时，设计人员一般采用较少振型用于分析以获得精度可以接受的结果。然而大跨度钢桁梁桥沿用此分析习惯，却可能严重影响其反应谱分析结果的正确性。为说明参与组合的振型数目对响应结果的影响，本文对钢桁连续梁特大桥进行了纵向地震下考虑第20阶振型、第22阶振型（包括18#墩自振）、第250阶（纵向参与质量94%）振型时的反应谱分析。因纵向地震响应主导振型的能量耗散机理，主要为下部桥墩钢筋混凝土材料的重复弹性变形的热效应，以及混凝土微裂缝的张开与变形等，故结构振型阻尼比按混凝土结构取0.05，振型组合方式为CQC。墩底内力响应结果如表2所示。

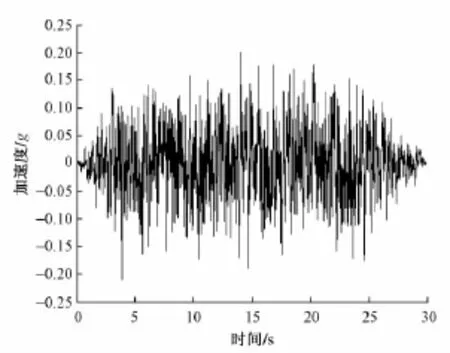
图3　人工波加速度时程曲线

表2　主墩墩底内力

由结构动力分析可知，18#墩墩身自振为0.405 s，位于场地反应谱峰值平台上，对其内力响应起主导作用，尽管18#墩不承受上部结构传递下来的地震力，其墩底剪力及弯矩响应值也接近设置固定支座的17#墩。

3种振型数目计算得到的19#墩梁端位移相同，均为66 mm。

分析结果说明，因下部结构质量较大，高阶振型对桥墩纵向地震内力响应影响较大，在反应谱计算分析时未考虑足够的参与计算振型阶数将导致结构内力计算结果失真，而纵向位移依然由低阶振型主导，取较少振型组合进行计算即可得到准确结果。

2.3.3时程分析要点

与反应谱方法仅能给出弹性结果和峰值响应结果不同，时程分析法计算能给出整个荷载激励历程内的结构响应变化情况，且能考虑诸多非线性因素，在大型桥梁抗震分析中具有极其重要的地位。

目前，桥梁结构时程分析中应用最为广泛的阻尼模型为瑞利阻尼，其表达式为

式中：M，K为质量、刚度矩阵；系数α和β由2个特定固有频率（圆）ωi，ωj和对应的振型阻尼比ζωi，ζωj从下式计算得到。

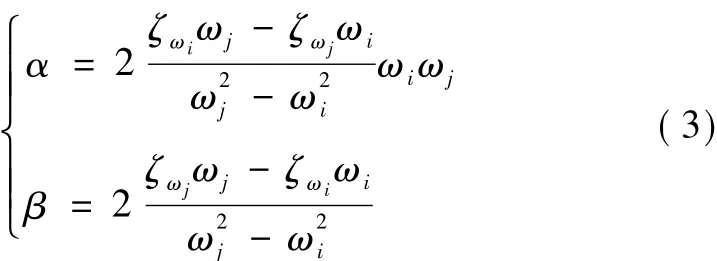
一般情况下，认为控制频率ωi和ωj的阻尼比相等，即ζωi=ζωj=ζ。当控制频率ωi和ωj选取不合理时，会使得各振型对应的阻尼比与实际不符，造成响应计算结果产生较大误差。研究表明，大跨桥梁选用计算方向参与质量大的前两阶（本文中的第20，22阶）振型确定的瑞利阻尼矩阵才比较接近结构实际情况［6］。对于本文所分析的大跨度钢桁梁桥，采用第1，2阶振型作为控制频率和选用纵向参与质量大的第20，22阶振型作为控制频率所计算的各阶振型对应阻尼比差异如图4所示。

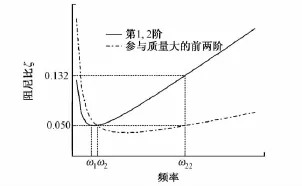
图4　不同控制频率计算的各阶振型对应阻尼比

2.4快速非线性时程分析（FNA）方法

与直接积分法需要形成阻尼矩阵不同，FNA方法可通过设定各阶振型的阻尼比来定义结构阻尼。FNA方法计算效率是常用的非线性时程直接积分法的数百倍［7］。在该方法中，非线性被作为外部荷载处理，首先形成考虑非线性荷载并进行修正的模态方程；然后基于泰勒级数对解的近似表示，使用精确分段多项式积分对模态方程进行迭代求解；最后基于前面分析所得到的非线性单元的变形和速度历史计算非线性力向量，并形成模态力向量，形成下一步迭代新的模态方程并求解。

其计算原理可表述为

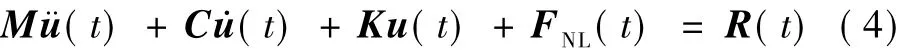
式中：M，C分别为结构的质量与阻尼矩阵；K为忽略了非线性单元的弹性刚度矩阵；FNL为每个时间点上迭代计算出来的非线性单元力总和的整体节点力向量；R为外部荷载。

在等式的两边同时加上“任意刚度的有效弹性单元”的节点力向量Keu（t），精确的平衡方程可写为

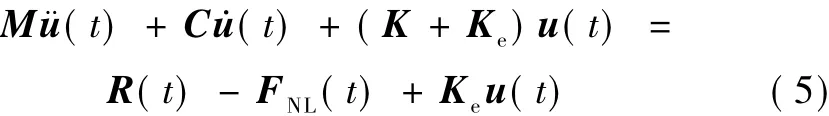
式中，Ke是不为0的任意有效刚度值。

图5、表3对比了瑞利阻尼矩阵计算控制振型为第1，2阶振型、计算方向参与质量大的前两阶振型，以及结构设定为常阻尼比0.05时3种阻尼确定方式下纵向地震荷载激励下内力和位移计算结果。其中，瑞利阻尼矩阵应用于直接积分分析法，常阻尼比0.05应用于FNA方法。

图5　不同阻尼确定方式下墩底内力对比

表3　3种阻尼确定方式梁端位移mm

由图5和表3可以看出，采用前两阶振型来确定瑞利阻尼矩阵时，中高阶振型阻尼比过大。将造成地震内力和位移响应结果特别是18#墩的内力响应结果远小于实际情况，计算结果偏于不安全。当采用常阻尼比0.05时，高阶振型未受到抑制，其计算结果与用计算方向参与质量大的前两阶振型确定瑞利阻尼矩阵时的分析结果相接近但略为保守。

3　结论

本文以一座全长504 m的3跨铁路钢桁连续梁特大桥为工程背景，对其抗震分析方法进行了分析讨论，研究结论如下：

1）大跨度铁路钢桁连续梁桥振型密集复杂，低阶振型多为上部结构自振，结构质量参与系数较低。延续常规混凝土铁路连续梁桥进行分析的习惯可能会影响反应谱分析结果正确性，参照公路和城市桥梁抗震规范，计算振型数目应保证计算方向的振型参与质量和超过90%。

2）大跨度铁路钢桁连续梁桥时程分析时采用第1，2阶振型来确定瑞利阻尼矩阵，将导致中高阶振型阻尼比过大，计算结果偏于不安全。瑞利阻尼矩阵计算控制振型应为计算方向参与质量大的前两阶振型以模拟实际情况。

3）与正确设定瑞利阻尼矩阵的直接积分时程分析计算结果相比，设置常阻尼比0.05，通过快速非线性时程分析方法（FNA）得到的内力计算结果略保守，而位移计算结果相似，在设计时偏安全。

［1］戴胜勇，艾宗良，杨善奎.客运专线四线双桁钢桁连续梁桥面系设计［J］.铁道建筑，2010（5）：12-15.

［2］左家强.太中银铁路中宁黄河特大桥桥式方案研究［J］.铁道工程学报，2013（12）：36-40.

［3］WILSON E L，DER K A，BAYO E P.A Replacement for the SRSS Method in Seismic Analysis［J］.Earthquake Engineering &Structural Dynamics，1981，9（2）：187-192.

［4］中华人民共和国交通运输部.JTG/T B02-01—2008公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［5］中华人民共和国住房和城乡建设部.CJJ 166—2011城市桥梁抗震设计规范［S］.北京：中国建筑工业出版社，2011.

［6］楼梦麟，张静.大跨度拱桥地震反应分析中阻尼模型的讨论［J］.振动与冲击，2009，28（5）：22-26，201.

［7］Computers and Structures Inc..CSI Analysis Reference Manual［Z］.Berkeley：CSI，2011.

（责任审编孟庆伶）

Seismic Analysis Method Study for Long Span Railway Steel Truss Continuous Girder Bridge

YANG Huaping1，SONG Chongyang2，QIAN Yongjiu1，LI Jing1，SHAO Changjiang1
（1.School of Civil Engineering，Southwest Jiaotong University，Chengdu Sichuan 610031，China；2.CCCC Second Highway Consultant Co.，Ltd.，Wuhan Hubei 430056，China）

In order to investigate vibration characters of long span railway steel truss continuous girder bridges and discuss key points of seismic response analysis of this type of bridges，a three-span railway steel truss continuous girder bridge with its total length of 504 m was modeled and analyzed with nonlinear finite element analysis program SAP2000.Analytical results show that the vibration modes of long span railway steel truss continuous girder bridges are more complex and the frequency spacing is smaller，compared with regular concrete continuous girder bridges. Response spectrum calculation with few combined modes，the method used for regular concrete continuous girder bridges，may cause unacceptable results.As for direct integral time history analysis with damping matrix using Rayleigh damping theory，two vibration modes with highest modal participating mass in the calculative direction shall be selected as calculation modes for damping matrix.W ith fast nonlinear analysis method for time history analysis adopting constant damping ratio 0.05，the results may be conservative.

Seismic analysis；Steel truss continuous girder bridge；Response spectrum；T ime history analysis；Damping

U442.5+5

A

10.3969/j.issn.1003-1995.2016.10.05

1003-1995（2016）10-0017-04

2016-05-17；

2016-07-28

国家自然科学基金项目（51178395）；四川省科技项目（2013GC0144）

杨华平（1989—），男，博士研究生。