任意初值非线性不确定系统的迭代学习控制

严求真　孙明轩　李鹤

任意初值非线性不确定系统的迭代学习控制

严求真1，2孙明轩1李鹤1

为解决任意初态下的轨迹跟踪问题，针对一类含参数和非参数不确定性的非线性系统，提出基于滤波误差初始修正的自适应迭代学习控制方法.利用修正滤波误差信号设计学习控制器，并以Lyapunov方法进行收敛性能分析.依据类Lipschitz条件处理非参数不确定性，对于处理过程中出现的未知时变参数向量，利用自适应迭代学习机制进行估计.经过足够多次迭代后，藉由修正滤波误差在整个作业区间收敛于零，实现滤波误差本身在预设的作业区间也收敛于零.仿真结果表明了本文所提控制方法的有效性.

迭代学习控制，初值问题，参数不确定性，非参数不确定性，Lyapunov方法

引用格式严求真，孙明轩，李鹤.任意初值非线性不确定系统的迭代学习控制.自动化学报，2016，42（4）:545−555

迭代学习控制技术问世于上世纪80年代初，适用于重复作业对象的控制器设计，可实现在整个作业区间上的零误差跟踪［1］.当系统在固定区间内重复运行时，可学习的不确定性虽然随着时间的变化而变化，但在各次运行中呈现相同的变化规律，沿迭代轴来看，同一时刻对应的不确定性为一常值.由此，可通过学习方法对其进行估计，并根据误差不断修正控制输入.这样，经过足够多次迭代运行后，可将闭环系统中可学习的不确定性予以完全补偿，实现系统状态对参考信号在整个作业区间上的完全跟踪［2−7］.至今，这种控制技术已应用于机械臂、磁盘驱动器和逆变电路等.

目前，基于Lyapunov方法设计学习控制系统引起了人们的关注［2−3］.在设计学习控制系统过程中，需要处理各种不确定性，常见的有线性参数不确定、非线性参数不确定性［8］和非参数不确定性［9］等.线性参数不确定性又可分为固定常数［10−11］、不随迭代次数变化的时变参数［12］，以及随迭代次数变化的时变参数［13］.从已经发表的文献数量来看，非线性参数不确定性和非参数不确定性方面的结果较少.文献［14］利用界函数设计反馈项补偿非参数不确定性.文献［15−16］结合使用鲁棒方法与学习方法处理非参数不确定性.傅里叶级数等逼近工具也可用于估计该类不确定［17］.文献［18］针对控制增益时变的非参数不确定系统，基于Backstepping方法设计迭代学习控制系统.文献［19］针对一类同含参数不确定性和非参数不确定性的非线性系统，分别提出准最优迭代学习控制算法和准最优重复学习控制算法.

在应用常规迭代学习控制算法时，需要在每次迭代开始前进行严格初始定位，以使系统初态与期望轨迹的起始点完全一致［3］.但在实际中，受复位条件的限制，系统存在非零误差初值.因此，研究适用于任意误差初值的迭代学习控制算法，不仅具有理论意义，还可拓宽迭代学习控制技术的应用范围.针对连续系统的Lyapunov方法初值问题解决方案见文献［20−22］.文献［20］提出了时变边界层解决方案.其控制策略是：经过足够多次迭代后，闭环系统的滤波误差可以收敛到与迭代初值相关的时变死区中.文献［21］给出误差跟踪设计方法，并将其与参考信号初始修正方法进行对比.文献［22］研究非参数不确定系统的误差跟踪学习控制算法.另外，在参考信号光滑闭合场合，可采用重复学习控制方法设计控制器，该法在运行过程中勿需停顿及复位［2，23−24］.

设计自适应或自适应学习控制器时，为了处理有界的不确定性，常采用鲁棒方法予以处理.根据界函数与符号函数设计反馈项可完全补偿不确定性，但据此设计的控制器在实现时容易发生颤振现象.为了克服这一不足，可以采用饱和函数代替符号函数，实现边界层外的切换控制和边界层内的线性反馈控制.类似的方法还有单位向量连续化［25］.在一些场合，例如根据反演方法设计控制器时，为了设计上的方便，可以采用双曲正切函数代替符号函数［26］.文献［27］利用双曲正切函数为严格反馈时变系统设计学习控制器.

为解决参数/非参数混合不确定系统的轨迹跟踪问题，针对任意初态的非严格复位系统，本文提出基于滤波误差初始修正的自适应迭代学习控制方法.在构造修正滤波误差后，采用Lyapunov方法设计迭代学习控制器并进行性能分析，利用鲁棒手段确保系统变量有界，处理非参数不确定性后，将所得的各未知时变参数合并为两个未知时变参数向量，并通过学习方法分别予以估计.经过足够多次迭代后，闭环系统的修正滤波误差在整个作业区间收敛于零，滤波误差在预设的部分作业区间上收敛于零.文中所给出的修正滤波误差构造方案，具有构造简单实现方便的特点.

1　问题描述

考虑有限时间区间［0，T］上重复运行的非线性不确定系统

假设1.函数

其中， θ（t）∈Rm为未知时变常数，为与θ（t）同维的连续向量，满足

此处，αf（·，·，·）为非负连续函数.

假设2.函数g（·，·）满足

其中，αg（·，·，·）为非负连续函数，且存在连续函数

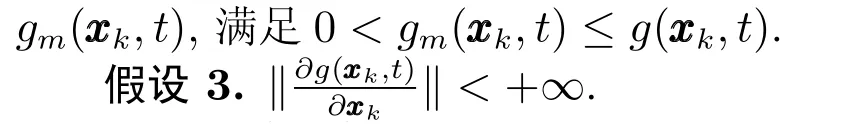
参数不确定性和非参数不确定性是系统中常见的不确定性，本文在假设性方面的要求较文献［28］低.为叙述简便，下文记分别为在不引起歧义时，函数的自变量t常被略去.

2　滤波误差初始修正下的控制器设计

记

选取合适的参数c1，···，cn−1，使得多项式∆（p）=pn−1+cn−1pn−2+···+c2p+c1为Hurwitz多项式.

定义1.

其中，φ（t）为一类连续可导的单调递减函数，满足φ（0）=1，φ（t）=0（∀t∈［t1，T］）.一种可选的φ（t）构造方案为

本文称sφk为修正滤波误差，其与误差的关系满足引理1.

证明.由式（4）知，

两边取范数

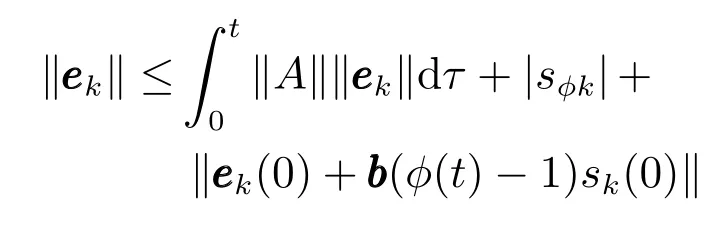
利用Bellman引理

在式（8）的两边同乘以e−λtµ|sφk|后取定积分，根据柯西不等式可以推得

上文给出了修正滤波误差与系统误差之间的不等式关系，在下文的控制器设计和收敛性分析中，将利用该不等式关系处理不确定性.

根据假设1和假设2，可以推出

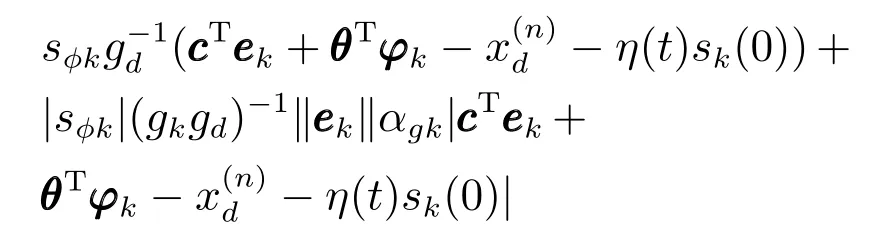
结合以上三式，有

其中，β1与β2的含义见引理1，为设计参数.

将上式的结果应用于式（9），有

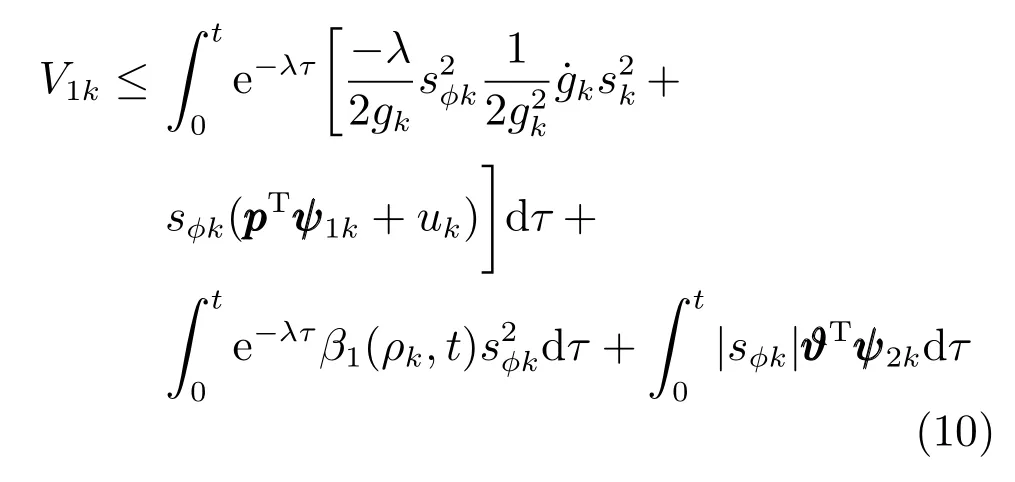
由此，设计控制律

3　收敛性分析

闭环系统具有的稳定性与收敛性方面的性质可总结为定理1.

并保证闭环系统所有信号有界.

证明.1）系统变量的有界性

结合以上两式，可以推出满足条件（22）时

由此可以得到sφk的有界性，在此基础上，结合饱和函数的性质，易得其他变量也为有界.

2）误差的收敛性

选择Lyapunov泛函

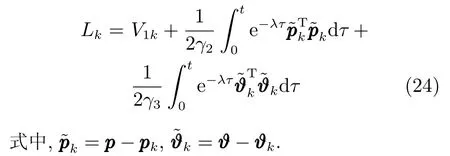
前文已证闭环系统变量均为有界，结合假设3，可知取足够大的λ，由式（10）和式（11），可得

成立.据此，可以推出

由式（26）及式（24），知

利用学习律（12）和（13），分别可以推出

将式（28）和式（29）的结果应用于式（27）

进一步地

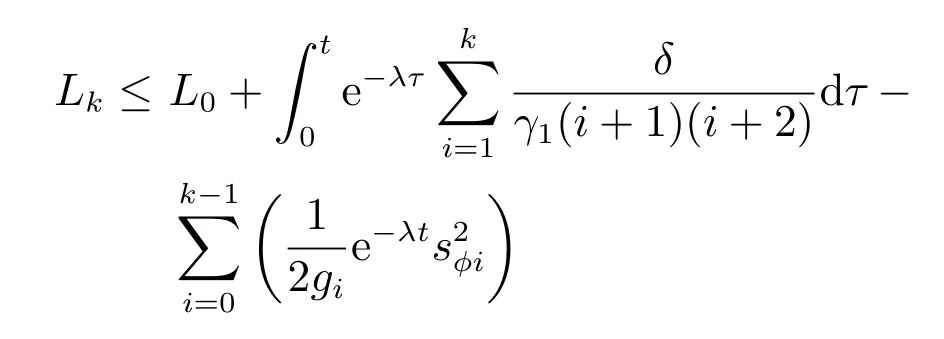
由于L0为非负有界量，且

是有界的，故根据数列收敛的必要性，可知

至此，根据sφk的定义，可得

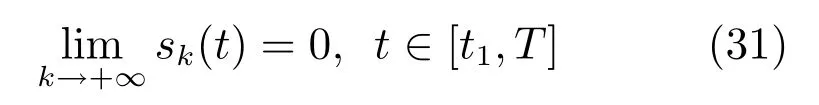
上文给出了基于滤波误差初始修正的自适应迭代学习控制方法，适用于系统初态任意情形.经过足够多次迭代后，籍由sφk在整个作业区间收敛于零，实现了sk在预设的部分作业区间收敛于零.

并保证闭环系统中的所有信号有界.

容易看出，修正滤波误差的构造方法简单.由上文的设计和分析过程可以看出，采用滤波误差初始修正方法设计控制器，勿需进行分类讨论，由此具有使用上的便捷性.经过足够多次迭代后，可实现滤波误差在预设的部分作业区间收敛于零.

4　仿真算例

考虑如下倒立摆系统

这里，x1k和 x2k分别是倒立摆的角位移与角速度，x1k（0）=1.2+0.1（r1−0.5），x2k（0）=−0.2+0.05r2，r1和r2均为0～1之间的随机数.g=9.8m/s2为重力加速度，mc=1kg是小车的质量，m=0.1kg为摆的质量，l=0.5m为摆长的一半，uk为小车的推力.参考信号是视和分别为∆fk和gk.考虑到实际系统存在的多种不确定性和扰动，设各参数与标称值存在±40%的偏差，取

采用控制律（11）及相应学习律进行仿真.仿真参数取γ1=1，γ2=5，γ3=0.01，ε=100，=20，=80，c1=10，T=2，t1=0.3，β5=10，β1，β2，β3，β4的含义见前文.采用第2节给出的方案构造φ（t）.迭代30次后，仿真结果如图1～6所示.图1和图2是第30次迭代时的系统状态情况.图3和图4分别是第30次迭代过程中的状态误差和控制输入情况.图5是在k=1，5，10，20，30等次迭代过程中的滤波误差情况，可以看出，经过足够多次迭代后，可实现滤波误差sk在［t1，T］上的取值为零.图6是Jk的收敛过程，在该图中，Jk=maxt∈［0，T］|sφk（t）|.

图1　x1及其期望轨迹x1dFig.1　x1and its desired trajectory x1d

图2　x2及其期望轨迹x2dFig.2　x2and its desired trajectory x2d

图3　误差e1和e2Fig.3　The errors e1and e2

本文与文献［22］采用仿真模型相同，在上文的仿真中，参数学习律的增益取值为5，而在文献［22］的仿真中，学习律的增益取值为30.对比之下，本文所提方法在学习增益较小的情况下，仍具有较快的误差收敛速度.

为了进一步说明本文所提设计方法的有效性，下面采用文献［20］所提的时变边界层方案解决相同问题，迭代学习模糊控制器取

图4　控制输入Fig.4　Control input

图5　滤波误差skFig.5　Filtering-error sk

图6　Jk收敛过程Fig.6　The convergence performance of Jk

其中，

i=1，2.具体构造方法见文献［20］的第2节.不难看出与均为36维的向量.

仿真参数取γ4=γ5=γ6=γ7=γ8=γ9=5，的取值同前.迭代30次后，仿真结果如图7～11所示.图7和图8是第30次迭代时的系统状态情况.图9和图10分别是第30次迭代过程中的状态误差和控制输入情况.图11是Jk的收敛过程，在该图中，Jk=maxt∈［0，T］|svk（t）|.

对比图1和图2与图7和图8，可以看出本文提出的基于滤波误差初始修正学习控制方法和文献［20］所提的基于时变边界层的模糊学习控制方法，均可用于解决迭代学习控制的初值问题，实现系统状态对参考信号在部分作业区间上的精确跟踪.在作业周期的后半段，本文所提方法具有较好的误差收敛性能，由图3可见，误差曲线在作业周期后半段几乎完全为零，且曲线几乎没有波动；而在图9中，误差曲线在作业区间后半段存在一定幅度的波动.该现象产生的原因与修正滤波误差/时变边界层的构造方式有关.sφk（t）=0，t∈［0，T］蕴含

图7　x1及其期望轨迹x1dFig.7　x1and its desired trajectory x1d

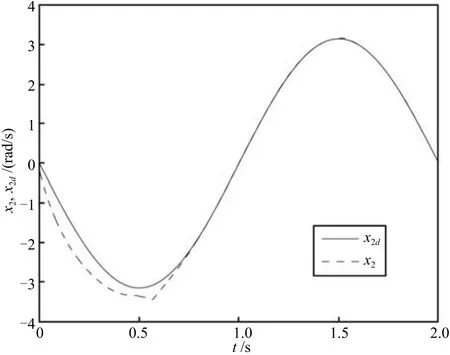
图8　x2及其期望轨迹x2dFig.8　x2and its desired trajectory x2d

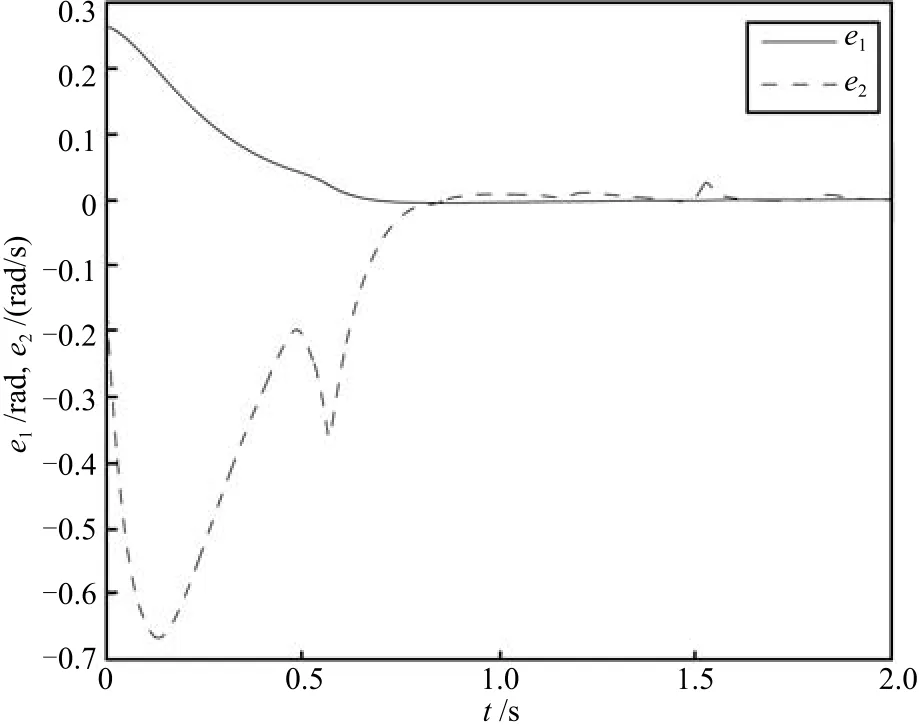
图9　误差e1和e2Fig.9　The errors e1and e2

图10　控制输入Fig.10　Control input

图11　Jk收敛过程Fig.11　The convergence performance of Jk

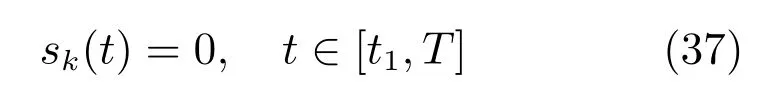
但 svk（t）=0，t∈ ［0，T］则意味着 sk（t）≤|sk（0）|e−σt，t∈［0，T］.对比图7和图11可以看出，本文所提方法在不使用高增益反馈的情况下，仍然具有较快的误差收敛速度和较好的控制精度.

仿真结果表明，利用本文给出的滤波误差初始修正方法设计学习控制器，可用于解决参数/非参数不确定学习控制系统的初值问题.使用这种方法进行控制器设计时，可以比较方便地构造出修正滤波误差，由其设计的控制器具有较快的误差收敛速度，能够获得较好的控制精度.修正滤波误差的使用较为方便.上述结果说明了本文所提控制方法的有效性.

5　结论

本文提出基于滤波误差初始修正的自适应迭代学习控制方法，解决参数/非参数混合不确定系统在任意初态情形下的轨迹跟踪问题.这种设计方法处理非参数不确定性后，将系统中原有的非参数不确定性补偿问题转化为线性时变参数估计问题，达到简化设计的目的.文中所构造的修正滤波误差兼具构造和使用方面的便捷性.仿真结果表明，对比已有主流方法，本文所提方案可获得较快的误差收敛速度和较好的控制精度.

References

1 Arimoto S，Kawamura S，Miyazaki F.Bettering operation of robots by learning.Journal of Robotic Systems，1984，1（2）: 123−140

2 Dixon W E，Zergeroglu E，Dawson D M，Costic B T.Repetitive learning control:a Lyapunov-based approach.IEEE Transactions on Systems，Man，and Cybernetics，Part B，2002，32（4）:538−545

3 Xu J X，Tan Y.A composite energy function-based learning control approach for nonlinear systems with time-varying parametric uncertainties.IEEE Transactions on Automatic Control，2002，47（11）:1940−1945

4 Zhang Yu-Dong，Fang Yong-Chun.Learning control for systems with saturated output.Acta Automatica Sinica，2011，37（1）:92−98（张玉东，方勇纯.一类输出饱和系统的学习控制算法研究.自动化学报，2011，37（1）:92−98）

5 Xu Xin，Shen Dong，Gao Yan-Qing，Wang Kai.Learning control of dynamical systems based on Markov decision processes:research frontiers and outlooks.Acta Automatica Sinica，2012，38（5）:673−687（徐昕，沈栋，高岩青，王凯.基于马氏决策过程模型的动态系统学习控制:研究前沿与展望.自动化学报，2012，38（5）:673−687）

6 Zhang Li，Liu Shan.Basis function based adaptive iterative learning control for non-minimum phase systems.Acta Automatica Sinica，2014，40（12）:2716−2725（张黎，刘山.非最小相位系统的基函数型自适应迭代学习控制.自动化学报，2014，40（12）:2716−2725）

7 Bu Xu-Hui，Hou Zhong-Sheng，Yu Fa-Shan，Fu Zi-Yi.Iterative learning control for trajectory tracking of farm vehicles. Acta Automatica Sinica，2014，40（2）:368−372（卜旭辉，侯忠生，余发山，付子义.基于迭代学习的农业车辆路径跟踪控制.自动化学报，2014，40（2）:368−372）

8 Chen Wei-Sheng，Wang Yuan-Liang，Li Jun-Min.Adaptive learning control for nonlinearly parameterized systems with periodically time-varying delays.Acta Automatica Sinica，2008，34（12）:1556−1560（陈为胜，王元亮，李俊民.周期时变时滞非线性参数化系统的自适应学习控制.自动化学报，2008，34（12）:1556−1560）

9 Marino R，Tomei P，Verrelli C M.Robust adaptive learning control for nonlinear systems with extended matching unstructured uncertainties.International Journal of Robust and Nonlinear Control，2012，22（6）:645−675

10 French M，Rogers E.Nonlinear iterative learning by an adaptive Lyapunov technique.International Journal of Control，2000，73（10）:840−850

11 Ye X D.Nonlinear adaptive learning control with disturbance of unknown periods.IEEE Transactions on Automatic Control，2012，57（5）:1269−1273

12 Tayebi A.Adaptive iterative learning control for robot manipulators.Automatica，2004，40（7）:1195−1203

13 Yin C K，Xu J X，Hou Z S.A high-order internal model based iterative learning control scheme for nonlinear systems with time-iteration-varying parameters.IEEE Transactions on Automatic Control，2010，55（11）:2665−2670

14 Ham C，Qu Z H.A new learning control based on the Lyapunov direct method.In:Proceedings of the Conference Record Southcon/94.Orlando，FL:IEEE，1994.121−125

15 Xu J X，Yan R.On repetitive learning control for periodic tracking tasks.IEEE Transactions on Automatic Control，2006，51（11）:1842−1848

16 Jin X，Xu J X.Iterative learning control for outputconstrained systems with both parametric and nonparametric uncertainties.Automatica，2013，49（8）:2508−2516

17 Liuzzo S，Marino R，Tomei P.Adaptive learning control of nonlinear systems by output error feedback.IEEE Transactions on Automatic Control，2007，52（7）:1232−1248

18 Chen Peng-Nian，Qin Hua-Shu，Fang Xue-Yi.Iterative learning control for uncertain nonlinear systems with timevarying control gain.Journal of Systems Science and Mathematical Sciences，2012，32（6）:693−704（陈彭年，秦化淑，方学毅.控制增益时变的非线性系统的迭代学习控制.系统科学与数学，2012，32（6）:693−704）

19 Yan Qiu-Zhen，Sun Ming-Xuan.Suboptimal learning control for nonlinear systems with both parametric and nonparametric uncertainties.Acta Automatica Sinica，2015，41（9）:1659−1668（严求真，孙明轩.非线性不确定系统准最优学习控制.自动化学报，2015，41（9）:1659−1668）

20 Chien C J，Hsu C T，Yao C Y.Fuzzy system-based adaptive iterative learning control for nonlinear plants with initial state errors.IEEE Transactions on Fuzzy Systems，2004，12（5）:724−732

21 Sun M X，Yan Q Z.Error tracking of iterative learning control systems.Acta Automatica Sinica，2013，39（3）:251−262

22 Yan Qiu-Zhen，Sun Ming-Xuan.Error trajectory tracking by robust learning control for nonlinear systems.Control Theory and Applications，2013，30（1）:23−30（严求真，孙明轩.一类非线性系统的误差轨迹跟踪鲁棒学习控制算法.控制理论与应用，2013，30（1）:23−30）

23 Sun M X，Ge S S，Mareels I M Y.Adaptive repetitive learning control of robotic manipulators without the requirement for initial repositioning.IEEE Transactions on Robotics，2006，22（3）:563−568

24 Li X D，Chow T W S，Ho J K L，Tan H Z.Repetitive learning control of nonlinear continuous-time systems using quasi-sliding mode.IEEE Transactions on Control Systems Technology，2007，15（2）:369−374

25 Qu Z H，Dorsey J F，Dawson D M.Model reference robust control of a class of SISO systems.IEEE Transactions on Automatic Control，1994，39（11）:2219−2234

26 Ge S S，Hong F，Lee T H.Robust adaptive control of nonlinear systems with unknown time delays.Automatica，2005，41（7）:1181−1190

27 Zhu Sheng，Sun Ming-Xuan，He Xiong-Xiong.Iterative learning control of strict-feedback nonlinear time-varying systems.Acta Automatica Sinica，2010，36（3）:454−458（朱胜，孙明轩，何熊熊.严格反馈非线性时变系统的迭代学习控制.自动化学报，2010，36（3）:454−458）

28 Xu J X，Qu Z H.Robust iterative learning control for a class of nonlinear systems.Automatica，1998，34（8）:983−988

严求真浙江工业大学信息工程学院博士研究生.主要研究方向为学习控制.E-mail:zjyqz@126.com

（YANQiu-ZhenPh.D.candidate at the College of Information Engineering，Zhejiang University of Technology. His main research interest is learning control.）

孙明轩浙江工业大学信息工程学院教授.主要研究方向为学习控制.本文通信作者.E-mail:mxsun@zjut.edu.cn

（SUNMing-XuanProfessorat the College of Information Engineering，Zhejiang University of Technology.His main research interest is learning control.Corresponding author of this paper.）

李 鹤浙江工业大学信息工程学院博士研究生.主要研究方向为学习控制.E-mail:lihuoo@126.com

（LI HePh.D.candidate at the College of Information Engineering，Zhejiang University of Technology.Her main research interest is learning control.）

Iterative Learning Control for Nonlinear Uncertain Systems with Arbitrary Initial State

YAN Qiu-Zhen1，2SUN Ming-Xuan1LI He1

This paper presents a filtering-error rectified adaptive iterative learning control method to tackle the trajectory-tracking problem for a class of both parametric and nonparametric uncertain systems in the presence of arbitrary initial states.A novel rectification is made to modify the filtering-error error signal such that the learning control design and performance analysis could be simplified and easy for implementation.The proposed learning control design is a Lyapunov synthesis-based adaptive iterative learning control scheme.The Lipschitz-like assumption is used for handling nonparametric uncertainties，where the estimation for unknown time-varying parameters is given by learning mechanisms. As iteration increases，the rectified filtering-error converges to zero over the entire time interval，and the filtering-error itself converges to zero on the specified interval.Numerical results are presented to demonstrate effectiveness of the proposed learning control scheme.

Iterative learning control，initial condition problem，parametric uncertainties，nonparametric uncertainties，Lyapunov approach

Manuscript July 27，2015；accepted November 17，2015

10.16383/j.aas.2016.c150480

Yan Qiu-Zhen，Sun Ming-Xuan，Li He.Iterative learning control for nonlinear uncertain systems with arbitrary initial state.Acta Automatica Sinica，2016，42（4）:545−555

2015-07-27录用日期2015-11-17

国家自然科学基金（61174034，61374103，61573320），浙江省高等学校访问学者专业发展项目（FX2013206）资助

Supported by National Natural Science Foundation of China（61174034，61374103，61573320）and University Visiting Scholars Developing Project of Zhejiang Province（FX2013206）

本文责任编委王聪

Recommended by Associate Editor WANG Cong

1.浙江工业大学信息工程学院杭州3100232.浙江水利水电学院信息工程学院杭州310018

1.College of Information Engineering，Zhejiang University of Technology，Hangzhou 3100232.College of Information Engineering，Zhejiang University of Water Resources and Electric Power，Hangzhou 310018