基于太阳定位的技术研究

王亚哲

郑州市第一中学

基于太阳定位的技术研究

王亚哲

郑州市第一中学

引言

太阳定位是通过某个时间段测量太阳的方位和高度角，从而获取点位的位置信息。太阳定位有多种用途，如在没有其它定位手段的前提下，只要通过一把尺子和确定的时间就可以获取当地的位置，对野外考察有重要的作用。也可以通过一段视频，要确定视频拍摄的地点，可以通过视频中物体的影子计算出太阳的方位和高度角，从而计算出视频拍摄的位置。

1　定位模型的建立

假定某地的经度和纬度分别为L、B，当地正午时间为t，而北京时间是东经120度的当地时间，故在中国范围内通过各地的地方时可以求得当地的经度，即：

太阳的方位角α、高度角β和纬度B之间的关系可以用下式表示：

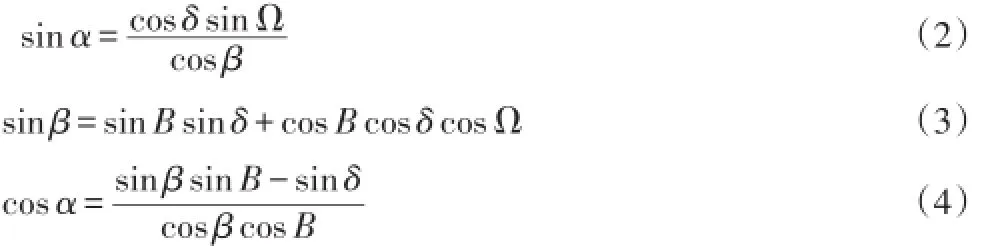
式中，

δ为赤纬角，sinδ=0.39795·cos（0.98563·（N-173）），N为从每年的1月1日开始计算到当日的日数。

Ω为时角，Ω=15×（t-12）；

从式（1）可以看出，如果要求当地的经度，必须先求得当地的正午时间。从（2）（3）（4）可以看出，如果要求当地的纬度，必须知道某地测量时的时角和太阳的高度角β和对应的方位角α。下面讨论如何求得当地的正午时间，以及太阳的高度角和方位角。

由（3）（4）式联立，可解算出纬度B：

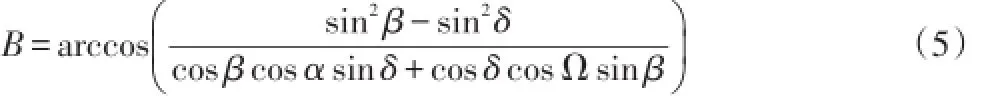
假定要求某地位置处有一个直杆，其高度为H，由于太阳的高度角的原因，在地面上投射了影子，影子的长度为l，则太阳高度角β和直杆高度H和影子长度l之间的关系为：

而当地的正午时间应是直杆影子最短的时间，可采用在一定时间段内对直杆影子进行观测并测量，获得直杆影子最短的时间，这个时间就是当地的正午时间。由于测量不是连续的，因此可对所测量的时间点进行曲线拟合，并对拟合后的曲线求取极值来确定高精度的当地正午时间。

假定在t0，t1，…tm个时间点测量直杆的影子长度分别为l0，l1，…，lm，设曲线方程为l=a0+a1t+a2t2，由于测量的数量多于方程的未知数，可采用最小二乘原理来计算曲线方程中的系数：

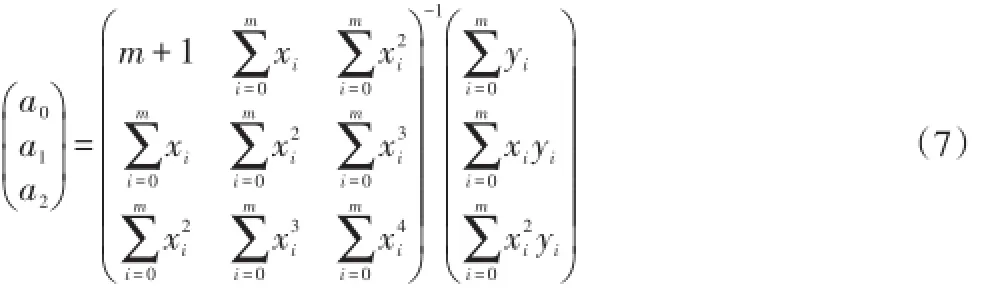
（7）式求出了曲线方程的系数，则可以根据曲线方程求出最短影长时的时间。

对曲线方程求导并令其一阶导数为零，可得：

从（7）可以得到影子最短的时间为：

（8）推出的就是当地的正午时间。

利用当地正午时间可以计算出当地的经度。利用计算出的时角和太阳高度角以及太阳方位角计算出当地的纬度。

2　计算流程与c++程序

利用太阳计算当地位置的流程图如图1所示。利用利用当地正午时间可以计算出当地的经度。利用计算出的时角和太阳高度角以及太阳方位角计算出当地的纬度。

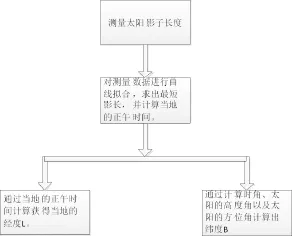
图1　利用太阳计算当地经纬度

本文利用c++编写了实用程序，程序首先应包含头文件math. h，定义#define PI 3.1415926，定义float a［3］，a1［100］［2］，b［3］［3］，b1［3］［3］，y［3］。a1［100］［2］用来放置观测数据，a［3］用来放置（7）的左侧部分，b［3］［3］用来得到（7）右侧第一部分中未进行逆阵运算的一部分，b1［3］［3］为b［3］［3］的逆阵，y［3］用来放置（7）式右侧第二项数据。利用求出的a［3］可直接计算出影子的最短时间为double t=（-1）*a［1］/（2*a［2］），输出经度语句为cout〈〈"经度="〈〈120+（12-t）*15；

纬度的计算：

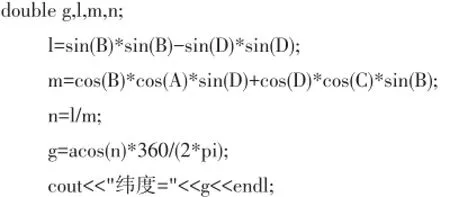
3　某地实测经纬度计算实例分析

2016年7月20日，在郑州一宽阔场地，从上午12∶20至13∶53利用杆高长度为1.590m的对中杆，由于当天的天气为多云，为了保证测量的精度，只选择了阳光比较好的时段进行了观测，这样每个观测时间段内并不均匀，本次共测设了17组数据，其实地观测图如图2所示，观测数据如表1所示。图2位实地测量图。

图2　实地观测图

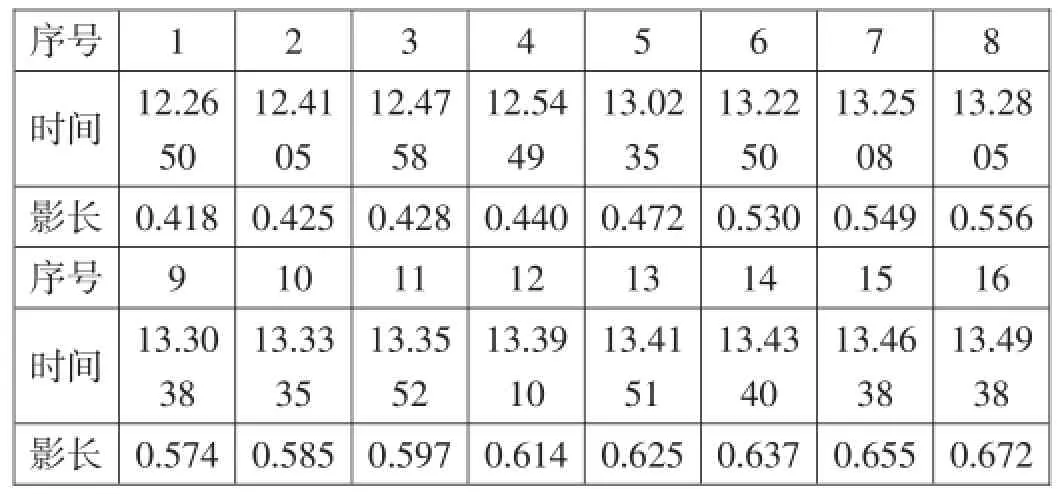
表1　太阳影长测量记录（时间单位为hh.mmss，影长的单位为m）

序号时间影长17 13.52 50 0.689

对上述测量成果进行曲线拟合，如图3所示可得：

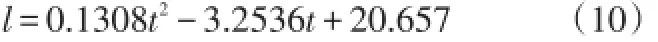
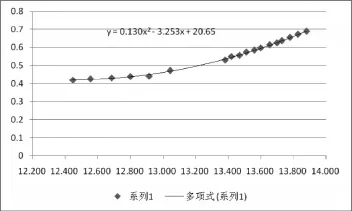
图3　二次多项式拟合图

根据公式（9），可以计算出当地的正午时间为12.437309h（12h26m14s），根据公式（1），可以计算出当地的经度为113∘.44037（113∘26′25"）。影长最短为0.424m。

通过公式（6），可以计算出太阳高度角β=75∘04′06"（75.06858），赤纬角为δ=20.4536131，时角为Ω=6.559635，可以计算出太阳的方位角为δ=24.545037，根据（5）可计算出当地的纬度为34.22934（34∘13′46"））。

根据和当地实际的经纬度比较，经度相差0.088度（约5’），纬度相差0.18度（约10’）。

4　结束语

利用太阳影子来计算当地的位置，在很多时候非常重要，本文首先根推出了曲线拟合影长和时间关系的算法，并利用求极值算法，计算出了最短影长和当地正午时间，并根据当地正午时间，计算出了当地的经度。根据文献，推导出了计算纬度的公式，并根据观测结果计算出了当地的纬度。结合本文的推导和实例分析，得到结论如下：

（1）利用太阳影子可以计算出当地较高精度的经纬度；

（2）计算太阳影子最短影长可利用曲线拟合对观测数据进行拟合，之后通过求极值方法计算出最短影长和当地的正午时间；

（3）要保证较高的精度，必须对杆子和影长测量准确，时间要和北京时间一致；

（4）选择投影杆子时，应尽量采用带有水平气泡的杆子，当无条件时，可利用铅坠，来保证投影杆子的垂直。

［1］黄玲，杨鹏辉，谢文，吴春艳.基于曲线拟合法太阳影子定位技术的研究.枣庄学院学报.2016，33（2），41-47

［2］胡毅华，杨旭龙，刘媛萍.关于太阳影子定位问题的求解.洛阳师范学院学报.2016，35（2），11-15

［3］徐微，曹小鸽.Matlab在太阳影子定位技术中的应用.通讯世界.2016（1），153

［4］蔡恩健，赵瑜，牛全福.以建筑工程测量法为基础建立影子长度变化的数学模型.城市建筑.2016（2）

Technology research base on the sun positioning

Wang yazhe
1middle school of Zhengzhou

通过太阳定位方法的探讨，推导出利用曲线拟合来拟合太阳影子和时间关系的曲线方程，并利用求极值方法计算出最短影长和当地正午时间，推导出进行经度、纬度的计算公式。通过实地进行杆子影长的测量，并根据C++进行编程计算，获得了当地的经纬度。

太阳；定位；经度；纬度

This paper discusses the sun positioning method，fitting curve equation of the sun shadow and time is derived using curve fitting.And calculate the shortest shadow and the local noon time using extreme value method.And deduced latitude and longitude’s formula.Through measure the poles shadow，and according to the c++ programming，obtained the local latitude and longitude.

the sun；positioning；latitude；longitude