《算法设计与分析》课程翻转课堂教学模式探究 

方洁

摘要：翻转课堂教学模式倡导以学生为中心和知识内化。结合《算法设计与分析》课程特点，利用微视频、网络教学平台等多种教学资源，将翻转课堂教学模式引入该课程教学，重点通过实例探讨翻转课堂模式应用思路。

关键词：翻转课堂；算法设计与分析；微视频；教学改革

DOIDOI：10.11907/rjdk.161608

中图分类号：G433

文献标识码：A文章编号文章编号：16727800（2016）009019903

作者简介作者简介：方洁（1983-），女，安徽安庆人，硕士，武汉工程大学邮电与信息工程学院机械与电气工程系讲师，研究方向为数据挖掘、分布式数据库。

0引言

近年来，翻转课堂、微课等教学方式在高校教学改革中兴起。对于理工科课程而言，知识点较难懂，学生需要时间消化吸收，因此更需要通过教学方式改革提高学生学习效率。翻转课堂是一种学生在课前利用教师制作的数字材料（音视频、电子教材等）开展自主学习，在课堂上参与探讨互动，并完成练习的教学方式[1]。探索该模式在《算法设计与分析》课程中的应用，达到提高教学效果的目的。

1课程特点及学习现状分析

《算法设计与分析》是一门计算机专业必修课程，需要将计算机经典问题与算法结合起来进行讲授。目前，大多高校该课程仍以理论讲授为主，学生被动接受知识，缺乏独立思考，一定程度上影响了教学效果。

1.1课程特点分析

《算法设计与分析》课程涉及的领域广，需根据学生基础不同进行内容调整和取舍，主要包括算法的基本概念、算法的基本工具和优化技巧、基本的算法策略（分治、贪婪、动态规划）和图的搜索算法（回溯法、分支限界法）。重点在于算法基本技巧和基本策略的学习，内容具有一定深度和广度。实际教学中，往往理论教学以教师课堂讲授为主，课时有限，学生参与较少；实验教学难度不好把握，过高往往导致学生失去信心，难度过低又会使学生失去学习兴趣，不能得到很好的训练。

1.2学生学习特点分析

笔者针对所在学院计算机科学与技术专业学生该课程学习情况进行了调查，总结如下：

（1）认为重复学习，学习热情不高。学习算法前学生已经学习了《数据结构》课程，部分内容与《数据结构》中的相似，因此部分同学认为是重复学习，学习热情不高。实际上，算法基本工具和优化技巧以及图的搜索问题，虽然学起来容易，但技巧应用较难，学生往往学完仍不会灵活运用。

（2）存在畏难情绪。由于学生学习基础不是很扎实，对于复杂算法的学习存在畏难情绪，只了解大致思想，缺乏钻研精神。

（3）课堂教学中不能积极主动参与讨论。由于该课程对学生理解和创新能力要求比较高，课堂上消化吸收所讲内容有一定难度，大部分同学很难参与讨论。

诸多学校对该课程的教学进行了改革，但只是在内容上更多的与实际相结合，以提高学生的学习积极性，在形式上采用启发式教学，加强创新性思维培养[2]。笔者教学过程中也尝试了这些教学方法进行，虽然能一定程度提高学生学习的兴趣，激发学生的创新思想，但教学效果还是差强人意。要让学生课堂上理解消化教师所讲知识，还要有所创新，举一反三，传统教学模式很难做到。采取翻转课堂教学模式，可有利于解决此类问题。

2翻转课堂教学方法

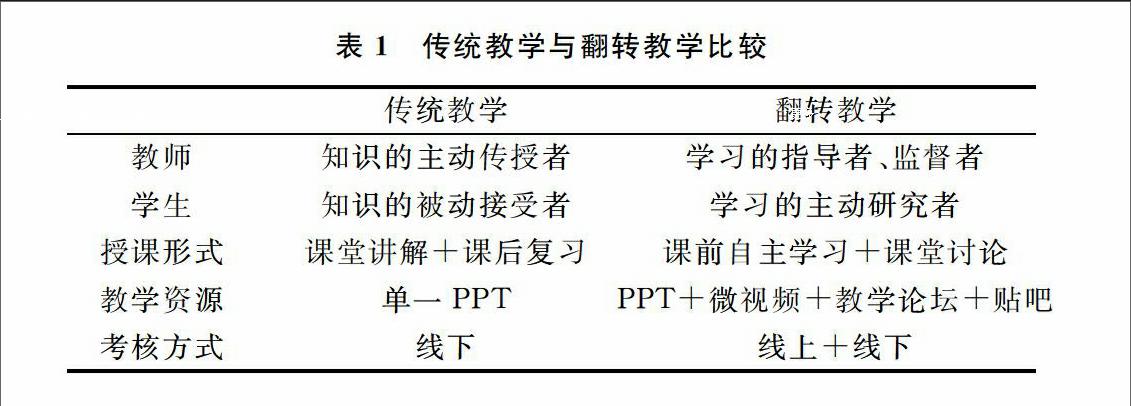
早在20世纪90年代初，哈佛大学物理学教授埃里克·马祖尔为解决课上传授知识为主造成学生对知识内容理解不透彻的问题创立了同伴教学法，要求学生课下自学课程内容，课上则以“提问-思考-回答”等互动为主[3]，这便是翻转课堂教学方法的雏形。传统教学中，大量时间用于课堂知识传授，学生利用有限的时间理解和思考老师所讲知识，并在课后对知识进行消化吸收。而翻转课堂中，学生课前利用充裕的时间主动学习老师即将讲解的课程，以各种形式向老师请教，课堂上老师和同学们互动，解答疑难，探讨创新。传统教学方法与翻转课堂教学方法比较如表1所示。

3翻转课堂设计

《算法设计与分析》课程有很强理论性，涉及数学模型及算法实现；同时又有很强的实践性，要将抽象的思维变为具体应用。针对学生特点，笔者采用清华大学出版社吕国英编著的《算法设计与分析》教材，实例较多，学生可以通过例题加深对各种算法的理解，方便开展翻转课堂教学。

3.1课前教学准备

（1）录制教学微视频。每个视频10～15分钟为宜，由于算法课程包含的知识点在数据结构课程中都已有所涉及，因此视频内容可分为知识回顾、核心算法策略讲解、算法扩展3个部分。

（2）搭建网络学习平台。申请视频服务器，构建教学网站，上传教学视频及开展网上交流讨论。

（3）归纳总结若干有关该算法的关键问题。一部分提前布置给学生，让学生带着问题观看教学视频；另一部分则在课堂教学中进行小组讨论。

（4）培养学习团队。根据先修课程中程序设计和数据结构课程的成绩，将学生分为5～6人一组，高分和低分互补，组与组之间的水平大致相当。

与传统教学不同，学生的主要任务是在课前观看教学视频并思考老师所提问题，将作业上传至网络教学平台，提出问题并通过网络学习平台请教老师。

3.2课堂活动设计

翻转课堂并不代表完全意义上的翻转，课堂上仍然需要教师对本节课知识点进行概括性讲解，并解答学生观看微视频中提出的共性问题。此外，教师要组织学生进行小组讨论，以2学时为例，可提供4个问题，每个问题给出10分钟左右的讨论时间，讨论过程中教师在一旁指导。讨论结束后，组长汇总小组意见，并在课堂上进行汇报，与其它组进行讨论。

3.3学习评价设计

学习评价是整个翻转课堂中必不可少的环节，学生可以在评价阶段了解自己对知识的掌握程度。同时老师对学生自学能力的认可，可鼓励学生更好地进行后期学习。评价可由两种方式结合进行：

①根据课前问题回答情况进行评价；

②以小组为单位进行评价，根据讨论的深度、广度和准确度给出评价结果。

4翻转课堂应用实例

以该课程中基本算法策略中的“分治策略”为例，设计2学时的翻转课堂教学。

4.1课前准备

分治法是指将一个难以直接解决的大问题分割成规模较小的相似问题。在数据结构课程中已有涉及，例如折半查找、合并排序、快速排序、二叉树遍历等[4]。因此本节内容适合利用翻转课堂教学，有利于学生自主学习。

（1）教学微视频制作。内容如下：

复习数据结构中的折半查找算法，引入分治法的基本思想。微视频中需要动态展示出折半查找的变化过程，并讲解伪代码描述的折半查找算法，体现减治法的应用。通过回顾折半查找知识引入分治策略，描述算法设计模式。

讲解例题：金块问题。如：有一袋金块（共n块），最优秀的雇员得到其中最重的一块。假设有一台比较重量的仪器，希望用最少的比较次数找出最重的金块。微视频中以10个数表示10块金块的重量，将此问题转换为用最少的比较次数找出最大的数。

将I=（n，A（1），…，A（n））分成一些较小的实例来处理。例如，可以把I分成两个实例：I1=（「n/2」，A（1），…，A（「n/2」））；I2=（n-「n/2」，A（「n/2」+1），…，A（n））。

如果Max（I）表示I中的最大元素，则Max（I）等于Max（I1）和Max（I2）中的较大者。如果I只包含一个元素，则不需要作任何分割，直接求解。

微视频中以动画形式展示利用分治策略求解最大值的过程，讲解算法思想及对应的伪代码。

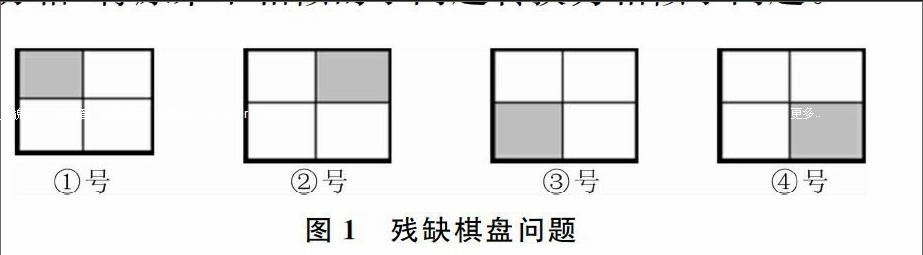
讲解例题：残缺棋盘问题。如：残缺棋盘是一个有2k×2k（k≥1）个方格的棋盘，其中恰有一个方格残缺。要用图1中的4种三格板覆盖更大的残缺棋盘。要求：每两个三格板不能重叠；三格板不能覆盖残缺方格，但必须覆盖其它所有方格。

微视频中，首先以动画形式展示4×4的残缺棋盘的构造过程，再推广到2k×2k的残缺棋盘，通过设置“伪残缺方格”将原来不相似的子问题转换为相似子问题。

（2）提出算法相关问题。要求学生带着问题观看视频，总结以下问题的答案，并上传到网络教学平台。

①除了折半查找，数据结构中还有哪些知识运用了分治策略；

②金块问题利用普通排序和蛮力策略分别如何解决？算法时间复杂度为多少；

③金块问题中利用分治策略解决了最大值问题，请写出最小值问题的求解算法；

④对于2k×2k的残缺棋盘问题，一共需要多少块三格板；

⑤微视频中残缺棋盘问题的子问题是以左上部分为例进行讲解的，能否描述出剩下3个部分的几个关键参数？

4.2课堂教学

首先讲解分治策略的基本思想，并围绕学生提交的答案，解决共性问题。针对微视频讲解例题，提出以下问题进行小组讨论，由组长汇总陈述。关于分治策略设置如下问题：

①分治策略解决金块问题的算法时间复杂度是多少？请描述求解思路；

②金块问题采用的是分治策略中的几分法？请描述所采用分治法解决的问题所具有的特征；

③智力问题—找石头：现有8颗小石头和一架托盘天平。有7颗石头的重量是一样，另外一颗比其它石头略重，除此之外，这些石头完全没有分别。不得假设那颗重石头到底比其他石头重了多

少。请问：最少要称量几次，才能把那颗较重的石头找出来；

④残缺棋盘问题的时间复杂度是多少？从这个问题中你学到哪些知识？

各小组同学可对本组组长的陈述进行补充，并对其它组的不同观点进行讨论。最后由教师对所讨论的问题进行总结和评价。学生还可以通过微视频进行复习，弥补预习时对该知识点理解的不足，进行深度挖掘。

5结语

《算法设计与分析》课程采用翻转课堂教学能提高学生的积极性，有利于以学生为主体。同时将小组合作的理念融入教学中，培养学生团队合作精神。本文通过实例探讨了《算法设计与分析》课程中如何使用翻转课堂教学，借助信息技术手段，提高了教学质量和效率，激发了学生学习主动性和积极性。

参考文献参考文献：

[1]张国荣.基于翻转课堂的《大学计算机基础》课程改革新思路[J].大学教育，2013（13）：135137.

[2]陈蕾，张怡婷，许建.基于创新能力培养的算法设计与分析课程教学改革[J].计算机教育，2010（20）：2729.

[3]杨斌，王以宁，任建四，等.美国大学IPSP课程混合式翻转课堂分析与启示[J].中国电化教育，2015（2）：118122.

[4]吕国英. 算法设计与分析[M].北京：清华大学出版社，2009：139145.

责任编辑（责任编辑：陈福时）