基于压缩感知的智能天线DOA估计算法
2016-11-07夏莘媛高鹏飞
夏莘媛,高鹏飞,戴 静
(1.河北工业大学 电子信息工程学院,天津 300401;2.中国人民解放军95900部队,河南 开封 475000;3.华北理工大学 迁安学院,河北 迁安 064400)

基于压缩感知的智能天线DOA估计算法
夏莘媛1,高鹏飞2,戴静3
(1.河北工业大学 电子信息工程学院,天津 300401;2.中国人民解放军95900部队,河南 开封 475000;3.华北理工大学 迁安学院,河北 迁安 064400)
波达方向(direction of arrival, DOA)估计是利用具有一定空间结构的天线阵元对空间信源的来波方向进行估计。为解决MUSIC算法和ESPRIT算法在智能天线DOA估计中空间谱分辨率和抗噪声性能方面的不足,依据压缩感知理论的贪婪算法思想,将匹配追踪(matching pursuit, MP)算法和子空间追踪(subspace pursuit, SP)算法应用在DOA估计中,即提出2种新的算法MP-DOA和SP-DOA。这2种算法主要包括原子库建立、信号投影、最佳匹配原子筛选及信号特征提取等过程。4种算法的仿真实验与对比分析结果表明,MP-DOA算法在低信噪比情况下较其他3种算法性能更优越,SP-DOA算法在角度分辨率和对信源数的包容方面的性能较其他3种算法优越,也验证了应用压缩感知理论的优越性。
波达方向估计;压缩感知;匹配追踪(MP)算法;子空间追踪(SP)算法
0 引 言
智能天线是一种具有测向和波束形成能力的天线阵列,其中波达方向(direction of arrival, DOA)估计是利用智能天线阵元对空间信源的来波方向进行估计,它在智能天线系统中扮演重要角色[1]。常规波束形成(conventional beam-forming, CBF)算法是最早的 DOA 空间谱估计算法[2],随后Capon 算法较之CBF算法提高了谱估计算法的分辨率。由R.O.Schmidr[3]于1979提出并于1986年发表的MUSIC算法,则大范围地提高了DOA估计的算法性能,它通过利用噪声子空间与信号子空间正交计算出空间谱函数,然后搜索谱峰,得到了DOA估计的方向参数。同期由R. Roy等[4]提出的ESPRIT算法则避开了MUSIC 算法的模式,直接可以通过2个完全相同子空间之间的旋转不变性来得出信号相关参数的空间谱估计。现今,MUSIC算法和ESPRIT算法已成为智能天线DOA估计中最为经典且常用的2种算法。
由D. Donoho等[5]提出的压缩感知理论给数据采集技术带来了理论性突破,它打破了Nyquist采样定律,可以用远小于信号2倍最高频率进行采样,实现了采样效率更高、存储空间更少的信号采样方法来进行信号的采集。其理论思想是运用贪婪算法实现信号稀疏分解,然后通过观测矩阵实现信号重构。现今压缩感知理论在诸多领域开始得到广泛应用[6],比如在通信系统的信道估计中能够取得满意的估计效果[7]。
在智能天线DOA估计中,由于信号常常具有稀疏特性,因此,研究基于压缩感知的DOA估计算法具有重要的理论意义和应用价值。为此,本文将压缩感知理论中的匹配追踪(matching pursuit, MP)算法和子空间追踪(subspace pursuit, SP)算法应用于智能天线DOA估计之中,并与MUSIC算法和ESPRIT算法做比较分析,以验证应用压缩感知理论的优越性,并可进一步提高DOA估计的算法性能。
1 DOA估计数学模型
1.1基本数学模型
本文数学模型建立在N个远场的窄带信号入射到由M个天线组成的线性阵列上,即处理器接收来自M个接收通道的数据。在此情况下,M个天线在某一时刻接收的数据为
(1)
(1)式中:y(t)表示阵元接收数据;τij表示阵元间的延迟;ω0=2πf=2πc/λ,其中c为光速,λ为波长;s(t)表示入射到空间信号的原始信号;n(t)表示外加噪声数据。
可简化成矢量形式为

(2)
(2)式中:Y(t)为M×1维阵元接收数组;B为空间阵列的M×N阵元处理矩阵;S(t)为入射到空间信号的N×1维原始信号;N(t)为M×1维外加噪声数组。
由上可知,阵元间的延迟表达式若已求得,待定空间阵列的导向矢量便可求得,即DOA参数便可求得。
1.2相干信号源的数学模型
现实环境中需考虑信号源为相干信号的情况,如信源传播过程中随时间不同,沿多条路径传播引起延时干涉现象,信号源的相干检测是DOA研究的一个重要研究方向。当信源包含多个信号时,其中可能存在信号之间相干、相关、独立3种情况。对于平稳的远场窄带信号Si(t)与Sk(t),它们的相关系数定义为
(3)
易得|ρik|≤1对信号之间的相关性定义为
(4)
故可得相干源的数学模型为
(5)
(5)式中:X(t)表示阵列的快拍数据矢量;S(t)为入射到空间信号的原始信号;N(t)为外加噪声数组;A为变化系数矩阵。
1.3经典DOA估计算法描述
MUSIC算法的思路是首先求得线性阵列的接收数据的协方差,然后对协方差矩阵进行特征分解,进一步得出组成信号分量,信号子空间和噪声子空间,最后利用这2个子空间的相互投影为零计算出信号的方向参数[8]。
空间谱估计中的ESPRIT算法与MUSIC算法的基本原理相同,都是首先求解接收信号的协方差,然后对协方差矩阵进行特征分解,两者的不同之处也很突出,即ESPRIT算法较MUSIC算法计算量小,无需搜索谱峰。
2 基于压缩感知的DOA估计算法
压缩感知理论的第一步是对具有先验条件的原始信号进行稀疏处理,在稀疏处理过程中使用的是贪婪算法思想。贪婪算法是通过不断地最优迭代计算寻找子问题的最优解,进而最终实现全局问题的最优解。
由于本文针对DOA进行研究,而非解析原始信号的全貌,故只需求出带估信号的DOA特征即可,其他方面暂不考虑。因此,主要目标是运用贪婪算法求信号DOA特征的最优解,通过不断地追踪运算得到全局最优解,进而实现对DOA的估计。
下面主要描述基于匹配追踪的DOA估计算法(MP-DOA)和基于子空间匹配的DOA估计算法(SP-DOA)。
2.1基于MP算法的DOA估计
设研究信号为f,信号长度为N,则f∈H∈RH,H∈RH是N维正交希尔伯特空间。将信号分解在基数目为N的正交基上。由于基在信号空间的稀疏分布,信号能量分散于各个基上,这将导致信号的非稀疏表示。故只有使基在信号空间适当密集,信号便能被稀疏表示。而此时基可能不再正交,故此时的基称作原子,这些原子组成的集合为过完备原子库。
MP的信号分解方法过程如下。
先在满足(6)式的条件下筛选出接收信号的最匹配原子gy0。
(6)
(6)式中,
(7)
(7)式中,
考虑(8)式的选择规则,使|

(8)
不断重复这种筛选过程
(9)
(9)式中,gyk满足
(10)
只要信号的稀疏表示能不断优化,就重复上述过程,直到最优解出现为止。这就是贪婪算法的核心原理。
运用MP方法分解阵列接收信号,对阵列信号进行非正交分解。对于基函数可灵活选取,故可通过建立过完备原子库将信号逼近在基函数上,最后由分解系数得到对研究有用的信息。为了得到阵列信号DOA的信息,需建立原子库,即
(11)
根据搜索的分辨率要确立角度范围,设角度搜索参量M个,m决定原子参数y。在进行MP分解中,(10)式给出了最佳原子向量的选取约束,在此约束条件下,阵列接收信号进行MP分解,噪声与阵列信号相互独立,故噪声在匹配原子上的投影接近于零,即噪声被滤除。由此可知,通过对参量θm进行匹配迭代运算,便可寻找出最优匹配,此匹配包含原始信号的DOA信息。因此,根据原子参量m便可估计出阵列信号DOA特征。
其基本算法流程如下。
步骤1由信号模型建立过完备原子库,并按照需要设置搜索精度。
步骤2将线性阵元接收得到的信号分别按各原子、各阵元上双循环进行投影计算。并对每个原子对应的K个不同阵元的投影进行线性叠加,统计出各原子的投影和值。
步骤3根据信源的估计数目,设定一定的投影阈值α,筛选出最优原子组。
步骤4由原子参量m(其中包含DOA特征)得出阵列信号DOA的估计。
2.2基于SP算法的DOA估计
SP算法与MP算法都是运用贪婪运算过程实现信号的稀疏与重建。其区别只是在原子库的建立过程中,SP算法在迭代步骤中,同时对先前入选的原子进行检验,并保留符合筛选条件的原子。这必将在全局上保证信号重建的最优性。
SP算法的主要过程如下。
1)输入:K,A,y。
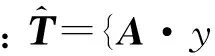

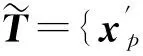
由于SP算法与MP算法相比,最大特点是在正交迭代的基础上将先前迭代过的原子进一步入选到残差中作为备选原子进行迭代分解,这一点反映在DOA估计中可进一步增加DOA估计的角度范围,提高空间谱估计分辨率。
设天线阵列的接收矩阵为X,即X为M列N行矩阵(M为阵元数量,N为快拍数),由于K个信源在各个阵元的接收阵列上是相互叠加在一起的,现要将方向信息从接收信号分别筛选出,需要将K个信源按方向特征进行分离。采用SP算法的大体思路是根据正交投影在完备的角度范围上投影得出信源包含的方向,即只有方向原子与信源方向信息之一完全一致时,投影值才能达到最大,才能实现最佳匹配。
其基本算法流程如下。
步骤1根据观测精度设置谱峰范围。
步骤2根据谱峰范围结合阵元结构构造原子库矩阵。
步骤3由原子库矩阵与接收信号矩阵相乘得到接收信号在原子库上的投影矩阵。
步骤4给投影矩阵的每一位采样点列向量按投影数值大小给原子标号进行由小到大排列,记录原子标号排列的新矩阵(原子标号中包含着信源方向特征)。
步骤5筛选出每一位采样点上投影值最大的原子标号,并组成一个行向量。
步骤6统计各原子标号出现最大值的次数,按照信源个数筛选出相应最优原子标号。
步骤7根据原子标号得到信源的DOA。
3 实验分析
3.1MP-DOA仿真分析
由算法原理编写基于MP-DOA算法的MATLAB程序, 选取5个彼此独立的且为远场窄带信号,信源的角度分别为-64°,-30°,20°,45°,70°,接收阵列为均匀线性阵列,阵元数目N=15,信源数目K=5,信号的中心频率为f,其对应的波长为λ,阵元之间的间距为d,且d=λ/2,快拍数为2 000。MP算法的仿真结果如图1所示。
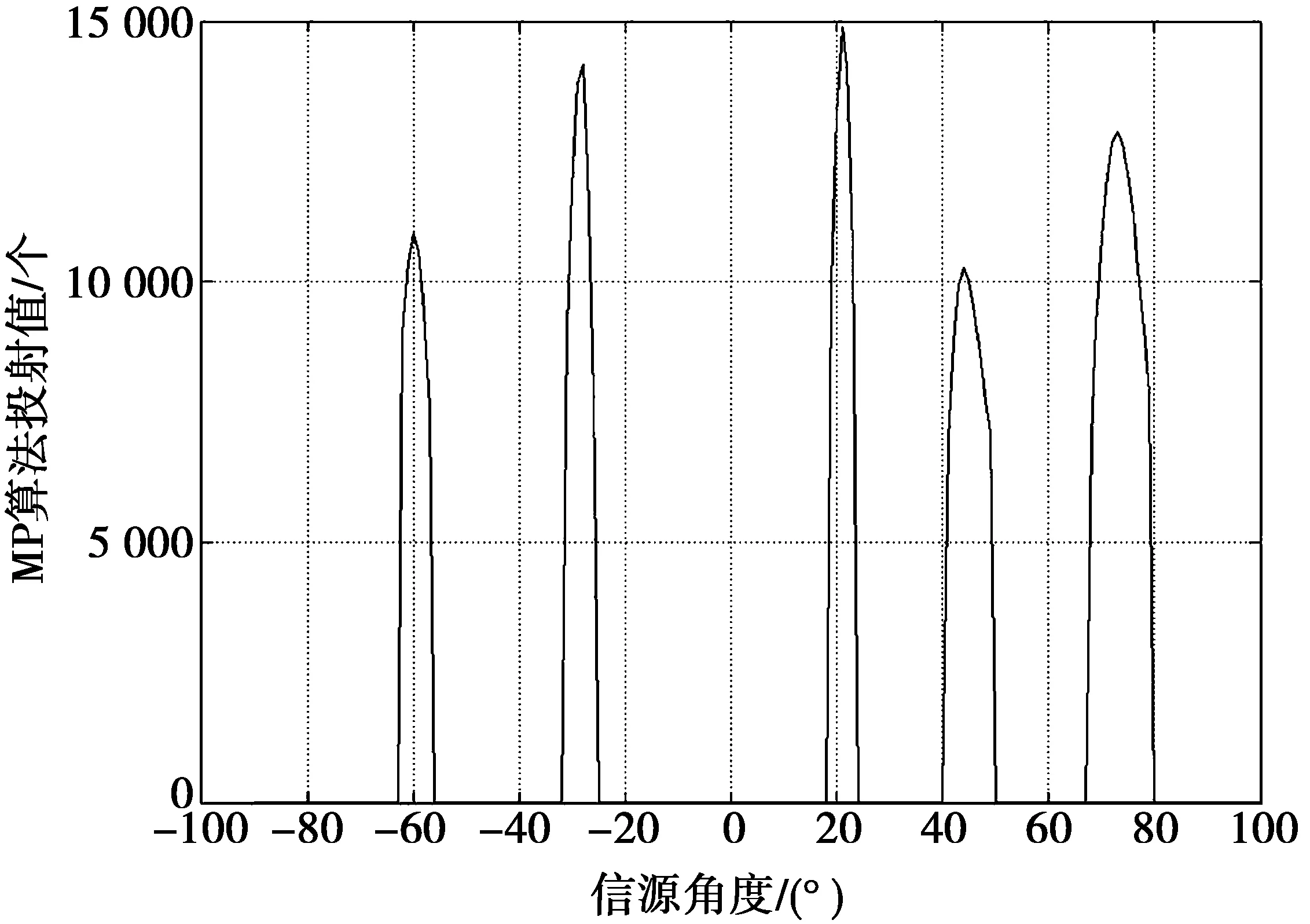
图1 MP-DOA算法仿真图Fig.1 Simulation result of MP-DOA algorithm
3.2SP-DOA仿真分析
由算法原理编写基于SP算法的MATLAB程序,选取5个彼此独立的且为远场窄带信号,信源的角度分别为-64°,-30°,20°,45°,70°,接收阵列为均匀线性阵列,阵元数目N=15,信源数目K=5,信号的中心频率为f,其对应的波长为λ,阵元之间的间距为d,且d=λ/2,快拍数为2 000。信噪比SNR分别为-20,-10,0,10,20 dB时得到仿真结果分别为DOA=-64°,-30°,20°,45°,70°。
3.3抗噪声能力性能分析
5个彼此独立的且为远场窄带信号,信源的角度分别为-64°,-30°,20°,45°,70°,接收阵列为均匀线性阵列,阵元数目N=15,信源数目K=5,信号的中心频率为f,其对应的波长为λ,阵元之间的间距为d,且d=λ/2,快拍数为2 000,计算SNR分别为-40,-30,-20,-10,0,10,20,30 dB时的空间谱估计标准差。得到4种空间谱估计方法的DOA估计值随信噪比SNR变化的仿真图如图2所示。
由图2可分析如下。
1)在信噪比低的情况下(-40—-10 dB),MP-DOA算法估计精准度最好,这说明在强噪声情况下,MP算法的抗干扰能力最强。
2)在信噪比相对较高的情况下(0—30 dB),SP-DOA算法估计精准度最好。标准差为零,即空间谱分辨率较高,这说明SP-DOA算法适应信噪比较高的空间谱估计。相比而言,MUSIC算法与ESPRIT算法在抗噪声性能方面存在劣势。

图2 4种算法抗噪声性能对比图Fig.2 Comparison on four kinds of algorithms at antinoise performance
进一步分析可知,MP-DOA算法优越的抗噪性是由其噪声向量不具备信号特征,在最佳原子向量的投影为零决定的。
3.4对阵元数的依赖程度性能分析
5个彼此独立的且为远场窄带信号,信源的角度分别为-64°,-30°,20°,45°,70°,接收阵列为均匀线性阵列,阵元数目N=15,信源数目K=5,信号的中心频率为f,其对应的波长为λ,阵元之间的间距为d,且d=λ/2,快拍数为2 000,计算阵元数分别为3,5,8,10,12,15时的空间谱估计标准差。得到4种空间谱估计方法的DOA估计值随阵元数变化的仿真结果如图3所示。
由图3可分析如下。
1)在阵元数分别为3,5的情况下,MP-DOA算法、MUSIC算法、ESPRIT算法的估计精准度几乎为零,标准差的计量已经失去了意义。但是为了便于比较,将其计入。
2)在阵元数较少的情况下(≤8),SP-DOA算法的空间谱估计精准,优势明显。进一步表明SP算法更加适应阵元数稀少的情况。
3)当阵元数大于8时,4种算法的性能都得到充分发挥,其中,SP-DOA算法在阵元适应能力方面的优势是压缩感知理论对信号的稀疏表示以及还原的强大能力的显现。
4)至于同样基于压缩感知理论的MP-DOA算法没有体现出这种优势的原因,在于这种算法在原子筛选的过程中,运用的是对于阵元的累加而非对最值进行筛选,故其对阵元数的依赖性较大。
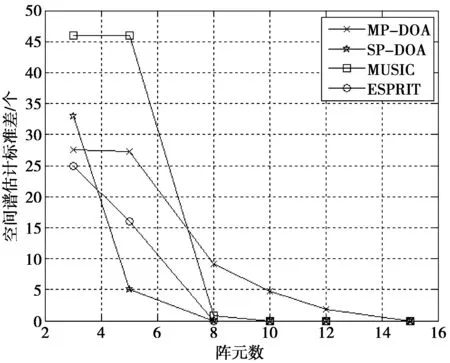
图3 4种算法受阵元数影响对比图Fig.3 Comparison on four kinds of algorithms at number of sensors
3.5对信源数的包容能力性能分析
接收阵列为均匀线性阵列,阵元数目N=0,快拍数为2 000,SNR为10 dB,信号的中心频率为f,其对应的波长为λ,阵元之间的间距为d,且d=λ/2,7种信源情况分别如下。
1)5个信源:(-64,-30,20,45,70);
2)6个信源:(-75,-42,-20,10,30,50);
3)7个信源:(-75,-60,-42,10,20,30,50);
4)8个信源:(-50,-30,-15,10,20,42,60,75);
5)9个信源:(-80,-50,-30,-15,10,20,42,60,75);
6)10个信源:(-80,-68,-50,-30,-15,10,20,42,60,75);
7)12个信源:(-85,-80,-68,-50,-30,15,10,20,42,60,75,85)。
分析在这7种信源情况下的MP-DOA算法、SP-DOA算法、MUSIC算法以及ESPRIT算法的空间谱估计正确率(误差不超过±2皆视为正确)。通过运行MATLAB程序,现将4种算法基于信源数量的正确率结果统计如表1所示。
由表1的结果进行分析对比,SP-DOA,MP-DOA算法在多信源情况下(信源数≥10)空间谱估计的正确率远远大于传统算法。这也表现了压缩感知算法在信号稀疏表示方面的优势。当信源的信息容量较大时,基于压缩感知理论的DOA估计算法能很好地从大容量信息中筛选出信号有用的特征信息,从而实现有效估计。

表1 4种算法基于信源数量的正确率(单位:%)Tab.1 Accuracy of four kinds of algorithms based on the number of signal sources(unit:%)
4 结束语
本文研究了2种基于压缩感知的DOA估计算法,并进行仿真实验与对比分析,结果表明,运用SP-DOA算法和MP-DOA算法可直接实现对相干信源DOA的估计,SP-DOA算法和MP-DOA算法较经典算法具有更强的抗噪声性能;在DOA估计算法受阵元数影响的指标中,SP-DOA算法性能优越性明显;在对信源数目的包容方面,SP-DOA算法和MP-DOA算法的性能要好于经典算法。这充分表明压缩感知理论运用到DOA估计的良好效果,体现了压缩感知理论的优势所在。
[1]SI Weijian,LAN Xiaoyu,ZOU Yan.Novel high-resolution DOA estimation using subspace projection method[J].Journal of China Universities of Posts and Telecommunications, 2012, 19(4):110-116.
[2]石国德,王明皓,吕朝晖.空间谱估计经典算法性能比较[J].电子设计工程,2013, 21(2):190-193.SHI Guode,WANG Minghao,LV Chaohui.Performance comparison of spatial spectrum estimation classic algorithm[J].Electronic Design Engineering,2013,21(2):190-193.
[3]赵谦,董民,梁文娟. DOA估计算法的一种修正MUSIC算法的研究[J].计算机工程与应用,2012,48(10):102-105.ZHAO Qian,DONG Min,LIANG Wenjuan.Research on modified MUSIC algorithm of DOA estimation[J].Computer Engineering and Applications,2012,48(10):102-105.
[4]刘晓莉,廖桂生.基于MUSIC和ESPRIT的双基地MIMO雷达角度估计算法[J].电子与信息学报,2010, 32(9): 2179-2183.
LIU Xiaoli,LIAO Guisheng.Combined MUSIC with ESPRIT Algorithm for Angle Estimation in Bistatic MIMO Radar System[J].Journal of Electronics and Information Technology, 2010, 32(9): 2179-2183.
[5]DONOHO D L.Compressed sensing[J].IEEE Transaction on Information Theory, 2006,52(4):1289-1306.
[6]司菁菁,程银波.融合压缩感知与网络编码的多速率与变速率传输[J].重庆邮电大学学报:自然科学版,2012,24(5):573-576.
SI Qingqing, CHENG Yinbo. Multi-rate and variable-rate transmissions realized by merging compressive sensing with network coding[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2012,24(5):573-576.
[7]ZHU Changjian, XIA Kewen, XIA Xinyuan, et al. Channel Estimation on 60GHz-ROF Downlink Based on Compressed Sensing[J]. Journal of Information and Computational Science, 2014, 11(16): 5727-5734.
[8]汤金燕, 谢跃雷, 彭诚诚. 基于MUSIC算法的球面共形阵DOA估计[J].电视技术,2014,38(11):150-15.
TANG Jinyan, XIE Yuelei, PENG Chengcheng. DOA Estimation for Spherical Conformal Array Antenna Based on MUSIC Algorithm[J]. Video Engineering, 2014,38(11):150-15.

夏莘媛(1992-),女,湖南人,硕士研究生,主要研究方向为通信信息处理技术。E-mail: will_9898@sina.com。

高鹏飞(1982-),男,山东乳山人,硕士,主要研究方向为智能信息处理。E-mail:712717@163.com。

戴静(1988-),女,河北秦皇岛人,硕士,主要研究方向为通信与信息系统。E-mail:djmagic@163.com。
(编辑:王敏琦)
s:The National Natural Science Foundation of China (51208168);The Tianjin Natural Science Foundation(11JCYBJC00900,13JCYBJC37700);The Hebei Province Natural Science Foundation (F2013202254, F2013202102); The Hebei Province Foundation for Returned Scholars (C2012003038)
DOA estimation algorithms in smart antennas based on compressed sensing
XIA Xinyuan1, GAO Pengfei2, DAI Jing3
(1.School of Electronics and Information Engineering,Hebei University of Technology, Tianjin 300401, P.R. China; 2.Troop 95900 of PLA,Kaifeng 475000, P.R. China; 3.Qian’an College, North China University of Science and Technology, Qian’an 064400, P.R. China)
Direction of arrival(DOA) estimation is realized by using antenna array with a certain spatial structure to estimate the arrival direction of space signal source. In order to solve the shortcomings in spatial spectrum resolution and anti-noise property of MUSIC algorithm and ESPRIT algorithm used in DOA estimation in smart antennas, based on the theory of compressed sensing basic idea of the greedy algorithm, the matching pursuit (MP)algorithm and subspace pursuit (SP) algorithm are applied in DOA estimation. Two new algorithms including MP-DOA and SP-DOA are presented, which mainly include the processes of the establishment of dictionary, the projection of signals, the screening of the best matching atom and the feature extraction of signals. The simulation experiment and analysis indicate that the MP-DOA algorithm is superior to other three algorithms in low SNR, and SP-DOA algorithm is superior to other three algorithms in angular resolution and number of signal sources inclusive. The superiority of compressed sensing theory is also verified.
direction of arrival estimation;compressed sensing ;matching pursuit(MP) algorithm ;subspace pursuit(SP) algorithm
10.3979/j.issn.1673-825X.2016.05.014
2015-02-21
2015-10-15通讯作者:戴静djmagic@163.com
国家自然科学基金(51208168);天津市自然科学基金(11JCYBJC00900, 13JCYBJC37700);河北省自然科学基金(F2013202254, F2013202102);河北省引进留学人员基金(C2012003038)
TN929.5
A
1673-825X(2016)05-0701-06
