基于预条件技术的风力机叶片计算方法研究
2016-11-07李雪斌来永斌周毅钧
王 龙,李雪斌,来永斌,周毅钧,张 瑾
(安徽理工大学机械工程学院,安徽 淮南 232001)
基于预条件技术的风力机叶片计算方法研究
王龙,李雪斌,来永斌,周毅钧,张瑾
(安徽理工大学机械工程学院,安徽淮南232001)
风力机叶片气动性能对风电机组功率输出具有重要意义和价值,正确的评估叶片性能有利于风力机选型设计工作。为此研究一种基于预条件技术的CFD计算方法用以风力机叶片气动性能评估。研究内容包括预条件处理、S-A一方程湍流模型等内容。利用C++语言开发气动计算程序,采用所开发的程序对某型风力机叶片算例进行气动模拟,获取流场及叶片表面压力系数分布。计算结果与实验吻合良好,所开发的程序可用于工程风力机叶片气动分析,有利于风力机设计工作开展。
预条件技术; 计算流体力学;风力机叶片
风能作为可再生资源的一种,其清洁低廉的特性受到世界各国的重视和欢迎。作为能量转化装置-风电机组,其性能高低直接制约能源利用效率[1-2]。而风力机叶片是风电机组的重要工作部件,其空气动力学问题是应关注的重点[3-5]。而计算流体力学方法[6-9]能够真实再现风力机运行过程中较高精度的流场拟序结构, 可处理其遇到的复杂流动问题。随着计算机的能力发展迅速,使得计算流体力学在风力机气动性能分析中占据的地位和作用愈加重要和明显。钟伟等利用sst湍流模型中的“β*最佳数值”改善NREL Phase Ⅵ风力机叶片在失速状态的数值模拟准确性。
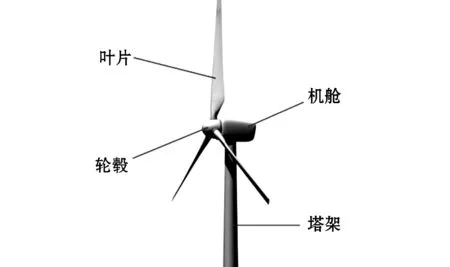
图1 风力机结构简图
传统可压缩计算流体力学算法用于低速流计算时会出现收敛变慢,计算不准确等问题,原因在于低速时控制方程系统矩阵特征值对应的特征波速相差太大,导致所谓的“刚性”问题[10]。为此,一些学者采用“预条件”技术克服这一问题[11-13]。张强等对迎风格式的低速预处理及远场边界影响研究,结果表明采用预处理后,合理的设置远场边界,可以进一步改善迎风预处理格式的收敛性和准确性[14]。
本文对流体控制方程组作预条件处理,通过改变系统特征值及特征向量,扩展可压流算法求解不可压流流动问题,可适用于风力机叶片低风速流动分析。基于C++平台开发数值计算软件,通过相关算例验证其正确性,所开发的软件适用于工程风力机叶片气动性能评估。
1 流体控制方程及湍流模型
自然界所存在的流体满足质量守恒、动量守恒和能量守恒三大规律,在忽略彻体力和源项的条件下,其数学积分的表现形式如式(1)~(3)所示。
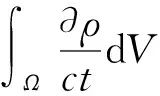
(1)
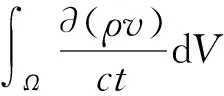
(2)
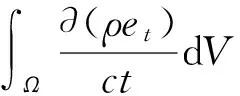
(3)
式中Ω表示空间内任一控制体的体积,由闭合曲面边界∂Ω围成。ρ、v分别为密度和速度矢量。p为应力张量,其牛顿流体的本构方程如(4)所示
(4)
S-A模型为Spalart和Allmaras于1992年提出的一方程湍流模型[15]。该方程在压声速和跨声速流动领域中的翼型及机翼应用广泛,对射流类湍流计算精度有些差强人意,但由于其只含一个湍流变量,因此相对于2方程模型来说计算量和耗时均较小。不引入转涙项的守恒型输运方程可改写为
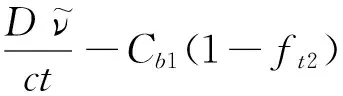
(5)
上式一些常数如下所示:Cb1=0.1355,σ=2/3,Cb2=0.622,其余表达式可参见文献[15]。
2 预条件技术及程序设计
预条件技术最初源于Turkel等人早期的文献,随后国外学者对其拓展和改进,如今已形成相当成熟的算法,可用于动/静网格下的定常/非定常计算。时间相关的守恒型N-S方程微分形式为
(6)
其中
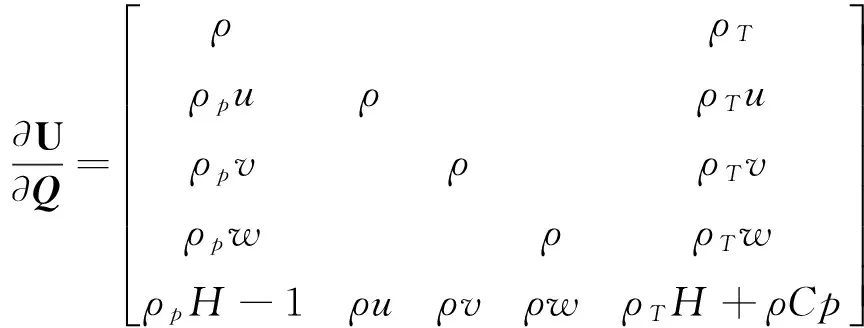
预条件后的控制方程组写作
(7)
给出最终推导的矩阵结果
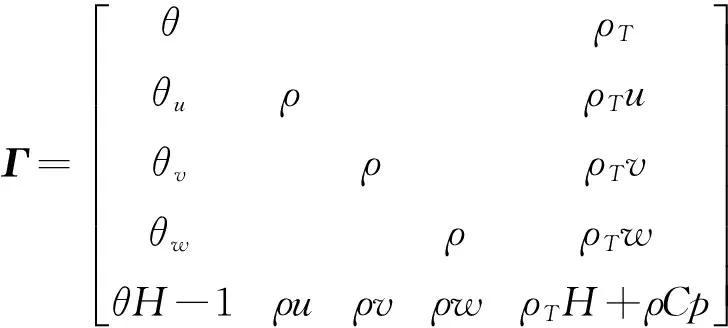
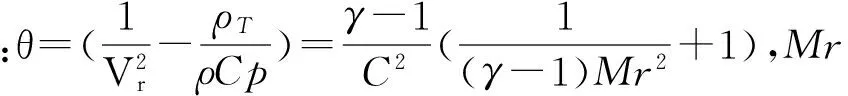
使用上式对控制方程进行改动,可扩展可压缩计算方法应用范围。流场计算简略过程为:首先读入网格文件,把相关几何数据信息分配至相应指针数组存储,之后读入控制文本文件,调用相关函数计算无黏通量,无黏通量采用“Roe”格式计算[17],之后计算方程组的黏性通量,通过对时间项的离散,把LU-SGS迭代所需相关数据事先存储起来,随后进行LU-SGS并统计流场残值,判断流场计算是否收敛。图2给出了总体方案设计流程图,图3则为dos窗口下的计算软件界面。
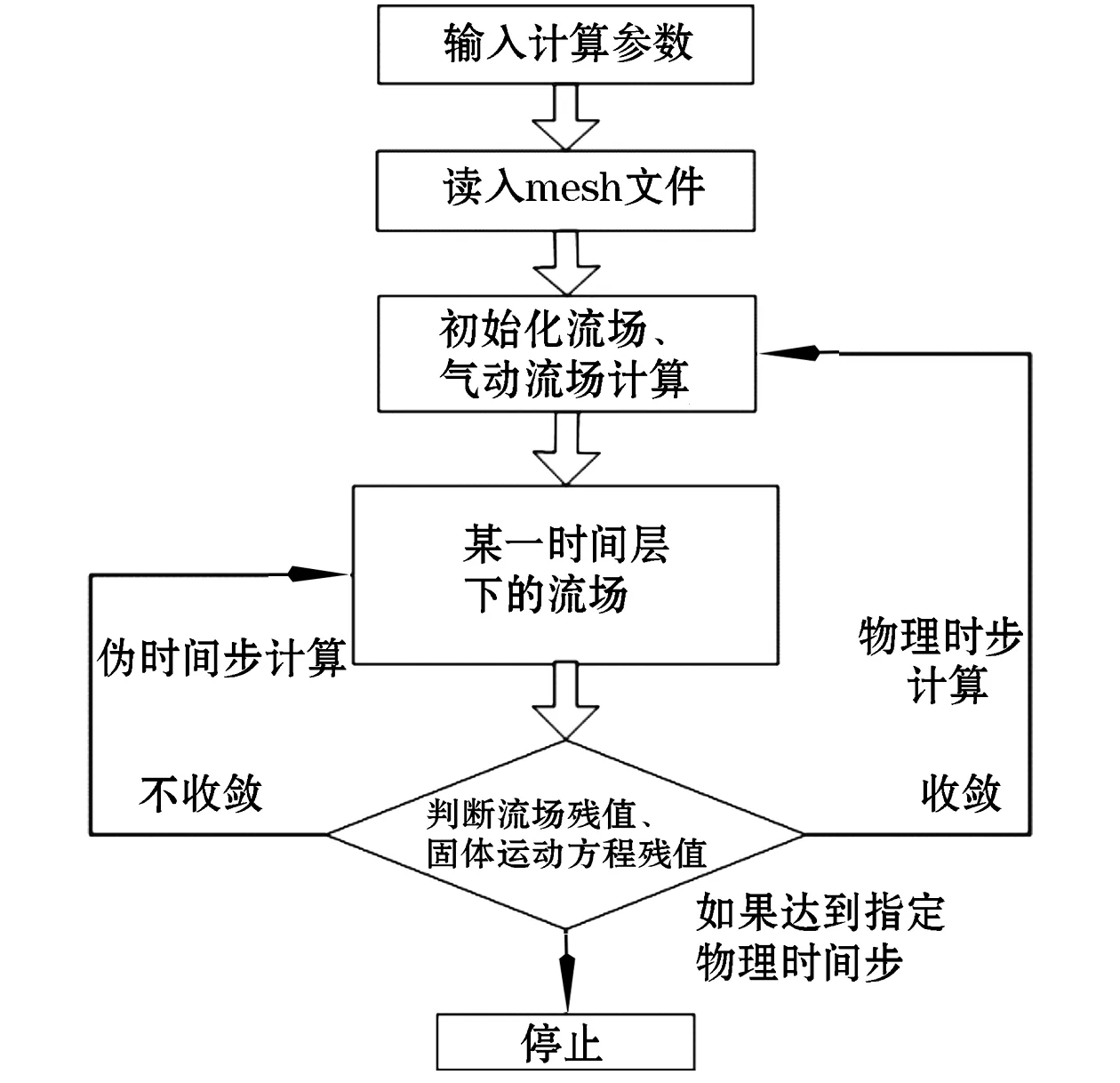
图2 总体方案设计流程图
图3 软件计算界面
3 计算结果
算例验证模型选用风力机标准叶片S809,叶片弦长为1m。来流空气的马赫数0.12, 属于不可压范围,雷诺数为2e6。图4给出了计算域划分图,计算域的上下边界为15倍弦长,为保证网格的正交性,计算域前部采用“C”结构,流体出口边界距离原点为30倍弦长。边界条件由远场及壁面组成。图5给出了网格示意,包括整体网格及风力机叶片前后缘局部网格,第一层网格距离壁面约为,总的网格数约为6万。边界条件可由文本文件读入,本文给定为壁面及远场边界条件。

图4 风力机叶片S809模型及计算域示意图

a.整体网格
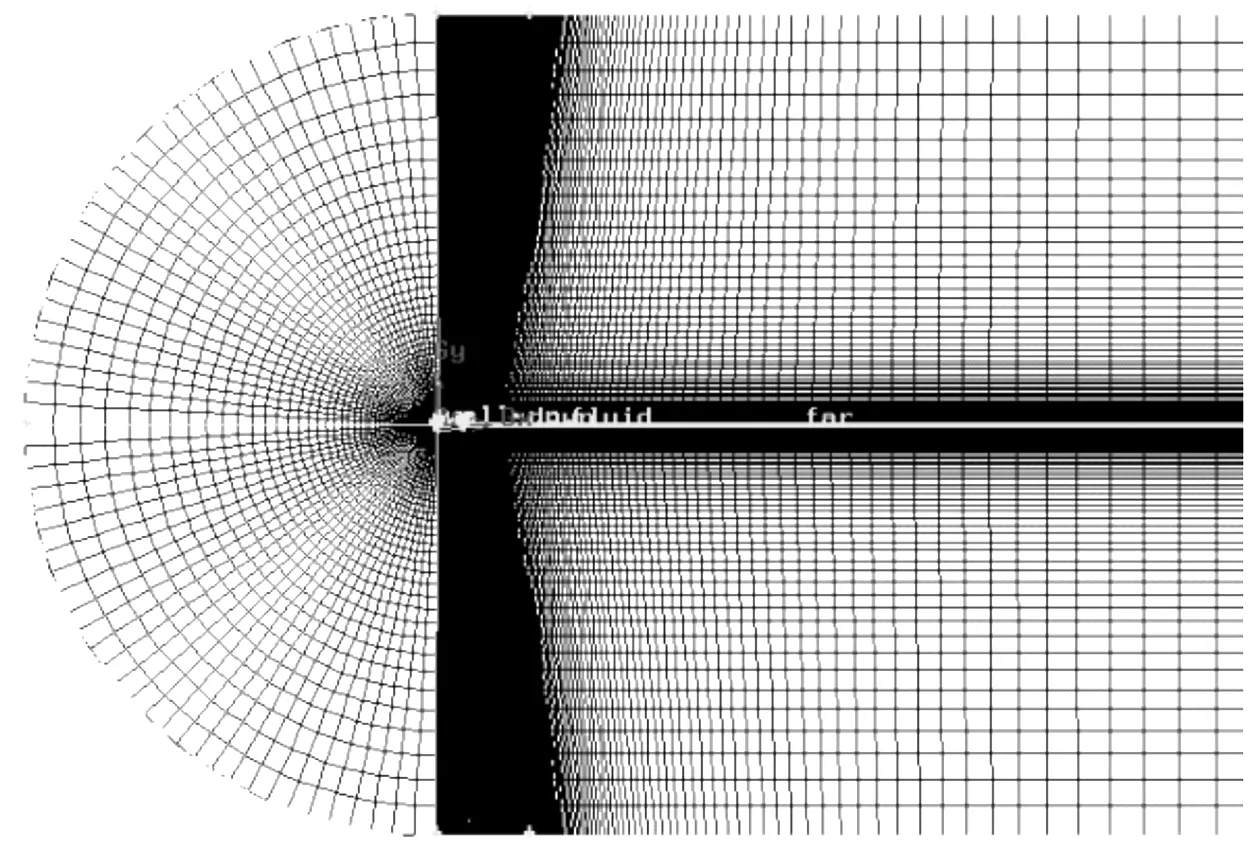
b.整体网格
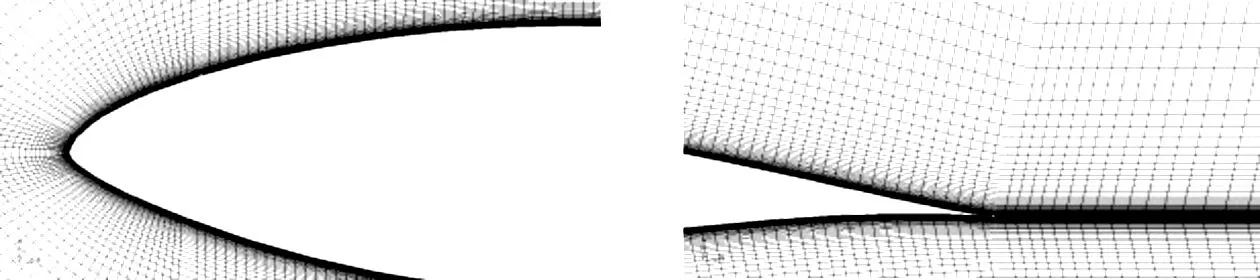
c.前缘 d.尾缘 图5 网格示意图
图6给出了加入预条件技术后的残值收敛历程。从图中可以看出在添加预条件技术后,速度残值先下降,之后趋于平稳,并出现一个上升的波峰,但随着迭代步的推进,残值迅速下降,各个变量的残值均位于10-5量级以下。也表明预条件技术可以改善动量方程的收敛性,获取较优的速度解,从而改善连续、能量方程迭代情况,最终使整个流场趋于真实物理解,而这与预条件技术提出的“初衷”是一致的。
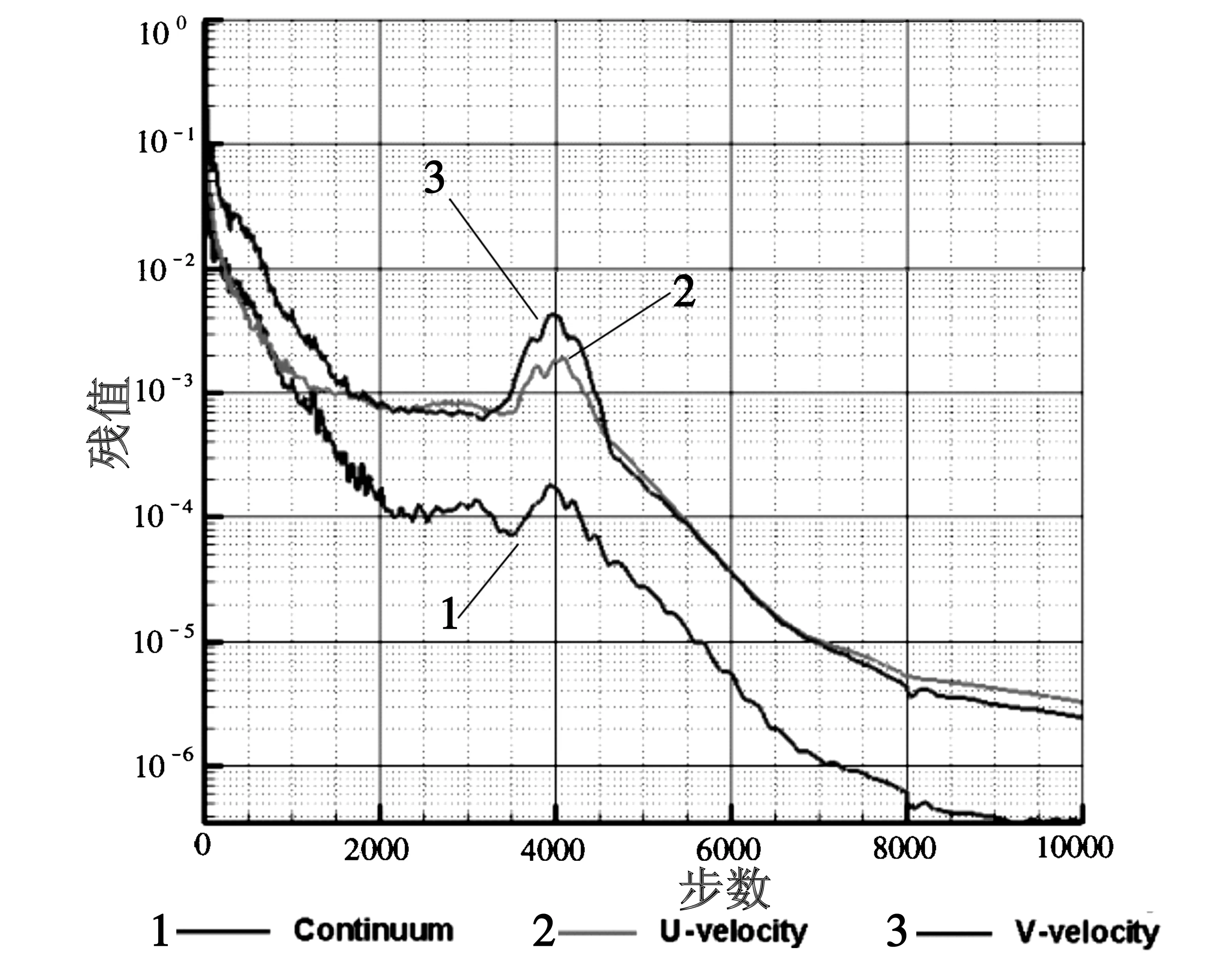
图6 收敛残值变化历程图
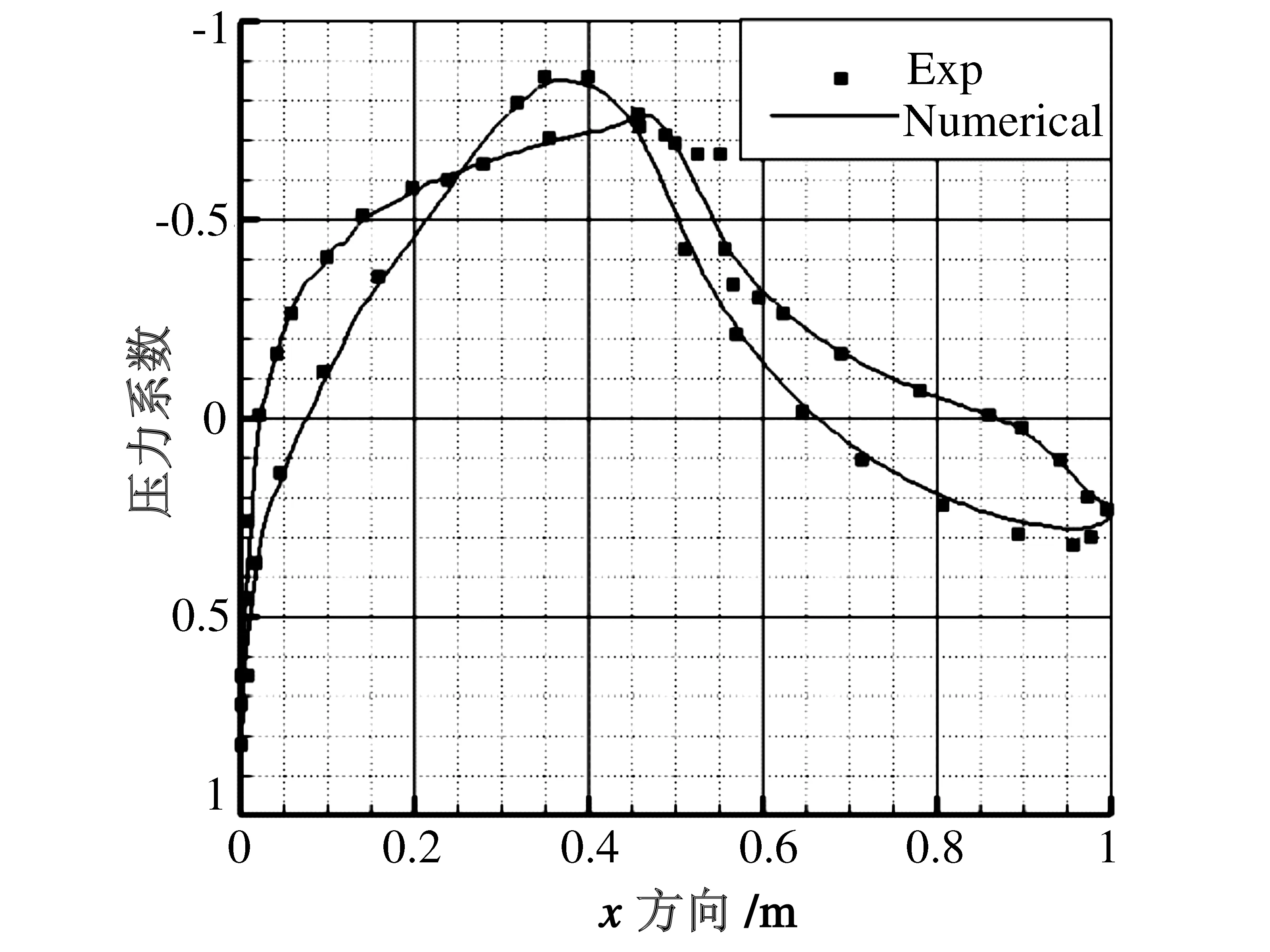
图7 叶片壁面压力系数
图7给出了0度攻角下流场计算收敛后所统计出的叶片上下表面压力系数,其中“Exp”表示实验值[18],“Numerical” 表示本文所开发程序计算结果。从图7可以看出,除极个别点外,本文计算压力系数不但分布趋势与实验走向一致,而且计算结果的精度与实验值吻合良好,验证了所开发程序的正确性。
图8为S809叶片在攻角为0-10度条件下的升力系数计算结果,从图中可以看出,在小攻角角度下升力系数与实验值吻合良好,在攻角为8度时计算值与实验室出现一定误差,随着攻角增加,误差开始变大,这是因为此时风力机叶片上表面尾缘处开始出现分离流动,数值计算结果的精确性完全取决于S-A湍流模型对该分离流模拟的真实性。但就小攻角计算结果而言,计算值与实验值吻合精确。
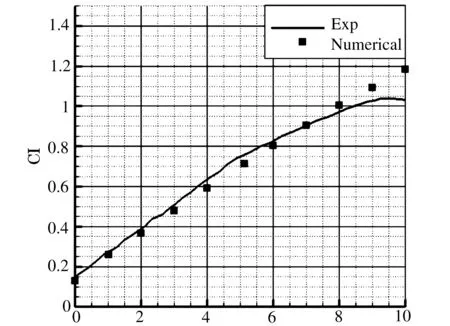
Angle of Attack
图9为0度攻角下流线分布图,此时流场没有出现分离现象,整体流动按照叶片设计工况发展,图中红圈蓝色箭头显示为前缘驻点。图10为攻角10度下的流线分布,可以看到前缘驻点下移,在接近叶片尾缘处出现分离泡,其范围折合X坐标约为0.93至0.994。

图9 风力机叶片0度攻角下流线图
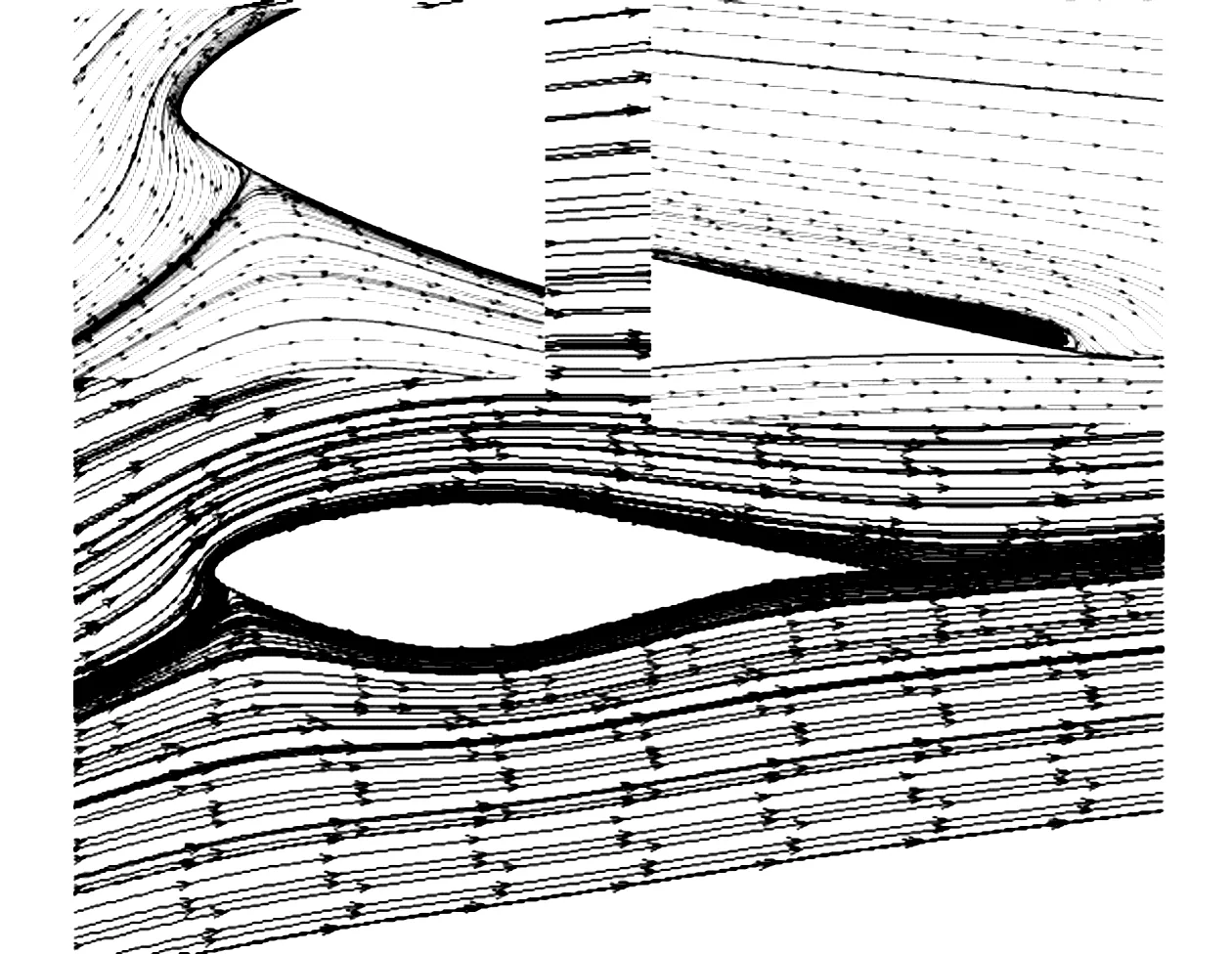
图10 风力机叶片10度攻角下流线图
4 结论
本文研究一种用于风力机叶片气动性能评估的计算方法,给出了推导的预条件矩阵结果,通过若干算例验证所开发程序正确性,得到结论如下:
(1)加入预条件矩阵以后,在低速流条件下,可压缩算法可以很快收敛,原因在于预条件技术可以改善动量方程的收敛性,获取较优的速度解;
(2)本文所开发的程序计算所获取的叶片压力分布系数与实验值吻合良好,同时计算小攻角条件下的升力系数与实验值一致,在攻角变大时会产生一定误差,此时尾缘出现分离,因此湍流模型及雷诺平均应力NS方程模拟对真实流场的模拟能力影响计算精度。考虑到工程实际需求,下一步需开发不同湍流模型用以大攻角下升力系数计算研究。
(3)考虑到风力机叶片气动性能对风电机组功率输出具有重要意义和价值,针对风力机选型设计工作的需求,本文所开发的工具可用于工程风力机叶片气动性能分析,有利于风力机设计工作开展。
[1]顾为东.中国风电产业发展新战略与风电非并网理论[M].北京:化学工业出版社,2006:8-100.
[2]吴治坚.新能源和可再生能源的利用[M].北京:机械工业出版社,2006:10-200.
[3]中国工程院. 中国能源中长期 (2030-2050) 发展战略研究 (可再生能源卷) [M].北京:科学出版社, 2011:7-50.
[4]李俊峰,蔡丰波,唐文倩,等.风光无限:中国风电发展报告2011[M]. 北京:中国环境科学出版社,2011:9-200.
[5]贺德馨.中国风能发展战略研究[J].中国工程科学,2011,13(6):95-100.
[6]钟伟, 王同光.SST湍流模型参数校正对风力机CFD模拟的改进[J].太阳能学报,2014, 35 (9): 1743-1748.
[7]周正贵.压气机/风扇叶片自动优化设计的研究现状和关键技术[J].航空学报,2008,29(2):257-266.
[8]OZGENS,CANIBEKM.Iceaccretiononmulti-elementairfoilsusingextendedmessingermodel.HeatMasstransfer, 2009, 45: 305-322.
[9]王龙,钟易成,吴晴,等. 双锥Bump压缩面设计及气动特性[J].航空动力学报,2013,28(01):82-89.
[10]TURKELE.PreconditioningTechniquesinComputationalFluidDynamics[J].AnnualReviewofFluidMechanics, 1999(31):385-416.
[11]TURKELE.PreconditionedMethodsforSolvingtheIncompressibleandLowSpeedCompressibleEquations[J].JournalofComputationalPhysics, 1987(72):277-298.
[12]TURKELE.AReviewofPreconditioningMethodsforFluidDynamics[J].AppliedNumericalMathematics, 1993,12(1-3):257-284.[13]TURKELE,RADESPIELR,KROLLN.AssessmentofPreconditioningMethodsforMultidimensionalAerodynamics[J],ComputersandFluids, 1997(26):613-634.[14]张强, 杨永. 迎风格式的低速预处理及远场边界影响研究[J]. 西北工业大学学报, 2012, 30(3):412-416.
[15]SPALARTP,ALLMARASS.AOne-EquationTurbulenceModelforAerodynamicFlows[R].AIAA-92-0439.
[16]WEISSJM,SMITHWA.Preconditioningappliedtovariableandconstantdensityflows[J].AIAAJ. ,1995,33:2 050-2 057
[17]RORP.ApproximateRiemannSolvers,ParameterVectorsandDifferenceSchemes[J].JournalofComputationalPhysics,1981(43):357-372.
[18]HARRISCDTwo-DimensionalAerodynamicCharacteristicsoftheNACA0012AirfoilintheLangley8-FootTransonicTunnel[R].NASATM-81927, 1981.
(责任编辑:李丽,吴晓红)
Research on Computational Method of Wind Turbine Blades Based on Preconditioning Technique
WANG Long,LI Xue-bin,LAI Yong-bin,ZHOU Yi-jun,ZHANG Jin
(School of Mechanical Engineering, Anhui University of Science and Technology, Huainan Anhui 232001, China)
Aerodynamic performance of wind turbine blades is significant and valuable for the wind turbine power output, so evaluating the blade performance correctly is advantageous to select and design the wind turbine. Therefore, the CFD calculation method based on a preconditioning technique was studied to evaluate the aerodynamic performance of wind turbine blades. The study included a preconditioning handling, an equation turbulence model of S-A etc. The aerodynamic calculation program was developed with the C++ language, which is for aerodynamic simulation of a certain type of wind turbine blades examples, to get the flow field and the pressure coefficient distribution of blade. The results are in good agreement with experiment,and the developed program can be applied to the wind turbine blades aerodynamic analysis in engineering as well as in favor of carrying out wind turbine design work.
preconditioning technique; computational fluid dynamics; wind turbine blades
2015-05-16
安徽理工大学国家自然(社会)科学基金预研资助项目(10029);安徽理工大学青年教师科学研究基金资助项目(12664);安徽理工大学引进人才科研启动基金资助项目(ZY041)
王龙(1984-),男,安徽蚌埠人,讲师,博士,研究方向:流体力学、风力叶片设计、叶轮机械、电磁散射等。
TK83
A
1672-1098(2016)04-0047-05
