基于客流的有轨电车发车时刻模型研究

巴宇航　姜　梅　郭孜政　陈崇双

(1. 西南交通大学交通运输与物流学院　成都　610031；2. 中国中铁二院工程集团有限责任公司科学技术研究院　成都　610031；3. 西南交通大学数学学院　成都　611756)



基于客流的有轨电车发车时刻模型研究

巴宇航1姜梅2郭孜政1陈崇双3

(1. 西南交通大学交通运输与物流学院成都610031；2. 中国中铁二院工程集团有限责任公司科学技术研究院成都610031；3. 西南交通大学数学学院成都611756)

阐明国内现有对公共交通发车时刻表的研究模型计算复杂，未考虑影响运营的多重因素，针对城市有轨电车系统，提出一种以车站客流量为依据、不均匀的发车时刻模型。首先以有轨电车最大、最小满载率和发车间隔作为约束，兼顾运营企业收入与有轨电车系统对乘客的服务水平；然后以断面客流作为确定发车间隔的依据，得到有轨电车的全天发车时刻表；最后通过影响发车的随机波动因素对发车时刻进行校正。该方法在实践中较以往的方法更加容易执行。

有轨电车；发车时刻；客流；满载率；发车间隔

现代城市有轨电车系统具有良好的适用性与经济性[1]，因此在大中型城市得到广泛利用。有轨电车运营调度的基础是制订合理的发车时刻表，时刻表的制订对电车发车计划与折返计划的制订与实施具有重要影响。

目前，国内对于公共交通发车时刻表的研究主要有以下两类：一类是研究基于各种智能的优化算法，代表性研究有王庆荣[2]、陈远[3]等人将遗传算法引入到公交排班问题的研究中，并对模型进行优化求解；另一类是研究基于实际运营调度的影 响 因 素，代 表 性 研 究有李英帅[4]等人依据客流在时间上的不均衡性优化了发车间隔，熊桂喜[5]等人建立了支持信号优先的快速公交行车时刻表优化模型，从而降低了车辆在交叉口的等待时间。

上述研究从不同层面完善了公交时刻表的制订研究，但仍存在一定不足：1) 智能优化算法比较复杂，求解困难；2) 对于发车时刻的制订未兼顾运营企业收入与公交系统对乘客提供的服务水平。鉴于以上不足，笔者提出一种基于客流并兼顾公交运营收入与乘客服务水平的有轨电车发车时刻模型，以期得到一种以客流量为基础，考虑多重运营因素的时刻表算法。

1　有轨电车时刻表制订影响因素分析

以客流数据、运营企业收入、有轨电车系统对乘客的服务水平以及影响发车间隔的随机波动因素作为制订有轨电车发车时刻表的依据。

乘客的活动具有规律性与周期性，具体表现在时间与空间上。客流在时间上具有不均衡性，早晚高峰的客流量比平峰要高，商业区的客流量在节假日比工作日要高[4]；在空间上，上下行不同站点的客流量不同，即客流同时具有空间不均衡性，这是由于客流量大小易受周边土地开发与经济发展情况的影响。在实际的运营过程中，只有适应客流实际时间、空间分布规律的时刻表方案，才可为乘客提供高质量的服务水平。

时刻表的制订应同时考虑运营企业收入与有轨电车系统的服务水平，即需平衡公交乘客和公交企业的利益，使两者尽量达到最大化[6]。时刻表发车间隔制订过密，易造成系统资源浪费，不利于运营企业的盈利与组织；发车间隔制订过大，易造成乘客等待时间过长和车内满载过高，会对有轨电车系统的整体服务水平产生不利影响。因此，发车间隔的制订应在考虑客流时空特征的基础上，综合上述两因素，具体通过发车时刻模型的约束条件进行界定。

由于现代城市有轨电车使用专用车道，因此影响发车的随机波动因素主要为电车在各站点、交叉口的等待时间。等待时间的大小由客流量大小、线路有无突发事件、交叉口的控制机制而确定。下面的算法以客流为基础，在制订发车时刻模型中还应考虑电车在交叉口的等待时间。

2　有轨电车发车时刻模型算法设计

2.1时刻表模型假设

1) 只考虑1条线路，共m个车站(i∈m)，对称设置在线路上下行方向。假设相邻车站之间只有1个交叉口，则整条线路共(m-1)个交叉口(j∈m-1)，电车在每个交叉口的停车时间为t1(j)；

2) 已知不同日期、时段、站点的客流数据，对应实际情况，已知高平峰时段的划分；

3) 车辆在线路上匀速行驶，行驶速度为v；

4) 有轨电车运营时间[tb,te]；

5) 每班电车编组数量、车辆型号一致。

2.2时刻表模型约束

2.2.1最大、最小发车间隔约束

考虑到乘客的等待时间与有轨电车系统能力，对相邻班次电车的发车间隔进行约束，即第k班和第k+1班电车的发车间隔在约束间隔时间以内，有

(1)

式中，t(k)为第k个班次在始发站的发车时刻。

2.2.2满载率的约束

考虑到乘客的舒适程度及运营企业的效益，对每班电车的满载率进行约束，有

ρmin≤ρi(k)≤ρmax

(2)

式中，ρi(k)为第k个班次在第i站的车辆满载率(i≤m)；ρmin为电车最低满载率；ρmax为电车最高满载率。

2.3时刻表模型建立

采集该线路上某一天不同时段站点的上、下车人数，按照以下步骤建立发车时刻表模型。

2.3.1建立净上车人数曲线

将每一站的上、下车人数等间隔按照统计时段采样，通过数据拟合得到该站全天净上车人数关于时间的分布曲线o(i,t)，则在[t1,t2]时段内，第i站的净上车人数为

(3)

净上车人数有时会出现负的情况，负的实际意义是在统计的[t1,t2]时段内，下车人数多于上车人数。

2.3.2电车在车站的计划停车等待时间

时刻表的制订需在初期计划每班电车在车站的等待时间。依据有轨电车运营时间内的上车人数，划分车站等级，不同等级的车站，计划电车在车站有不同的停站等待时间t2(i)。车辆在车站的停车时间视车站乘客数量多少而定。一般情况下，高峰时段由于乘客数量较多，停车时间较长；反之，平峰时段停车时间较短。

(4)

式中，t1,t2,…,tp为电车在不同等级车站的停站等待时间，t1>t2>…>tp；a1,a2,…，ap为车站的候车乘客数量，a1>a2>…>ap。

由此，将车站划分为p个等级，对不同等级的车站在调度初期就预留不同的停站时间，这样有利于合理分配发车间隔。

2.3.3客流平移与叠加

在通常的客流数据处理中，往往把各个站点调查的实际时间的数据作为调度的依据，忽略了车辆的行车时间对疏散客流的影响[7]。为此，笔者提出将客流曲线按时间平移的数据处理方法，将始发站之外的所有车站的客流全部平移叠加到始发站。

第i站到第i+n站的行驶时间为

(5)

其中，n=1,2,…,m-i。

那么当电车行驶到第i站(共行驶过j个交叉口，j=i-1)的延迟时间为

(6)

式中，t1(j)为电车在第j个交叉口的等待时间，则将第i站净上车人数分布曲线平移到始发站的曲线为

o’(i,t)=o(i,t+ty(i))

(7)

其中，2≤i≤m。

将所有车站净上车人数叠加到始发车站的分布曲线为

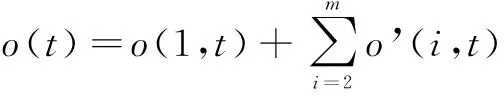
(8)

即客流净上车人数叠加曲线为始发站上车人数曲线与其余所有车站平移到始发站的累加曲线之和。

2.3.4确定发车间隔

依据不同的约束条件，求得每两个相邻班次的发车间隔，从而得到运营时间内所有班次的发车时刻。

已知第k个班次的发车时刻t(k)，那么发车后由于电车满载，车站上的滞留乘客数量为

(9)

式中，r(k)为第k班电车开走后车站的滞留乘客；lmax为电车达最高满载率时的载客量。

由此，可以由公式(10)、(11)计算得到第k班电车发车后第k+1班电车在达到最低、最高满载的时刻tu(k+1)、tv(k+1)。

(10)

式中，tu(k+1)为第k+1班电车达到最低满载时的发车

时刻；lmin为电车达最低满载率时的载客量。

(11)

式中，tv(k+1)为第k+1班电车达到最高满载时的发车时刻；lmax为电车达最高满载率时的载客量。

在高峰、平峰不同时段内，根据系统对断面客流的运载能力，设置计划发车间隔时间Δt。计划发车间隔的设置应尽量满足该时段内电车发车的班次对所有车站中最大断面客流的运输，一般平峰时段间隔大于高峰时段间隔。

以平峰时段[ta,tb]为例进行说明，统计该时段客流量最高的车站，以系统能力满足该断面客流设置计划发车间隔，有

(12)

Δt=(tb-ta)/nta,tb

(13)

式中：nta,tb为在[ta,tb]时段内的计划发车数目；ρ为电车运营计划满载率，一般通过考虑电车计划营业收入与对乘客的服务水平来确定；W为电车额定载客人数。

根据约束条件，得到第k+1班电车的发车时刻，有

(14)

对于公式(14)的解释为：按预定发车间隔的发车时刻早于最低满载发车时刻，则按照最低满载发车时刻发车；若晚于最高满载发车时刻，则按最高满载发车时刻发车；若在两个满载发车时刻之间，则按照预定发车间隔的发车时刻发车。当发车间隔超出最大、最小发车间隔范围时，根据超出的限界(超出的是最大或最小间隔)，选择最大或最小发车间隔作为发车间隔。

由此，在已知最早发车时刻的基础上，只需依据条件与约束依次计算下一班次的发车时刻，即可得到全天所有班次的发车时刻。

2.3.5基于交叉口等待时间的发车间隔校正

电车在交叉口的等待时间由电车到达交叉口的时刻与交叉口的控制机制决定，有

(15)

t(j,k)=min{tg(j)-t′(j,k)}

(16)

式中：t(j,k)为第k班电车在交叉口j的等待时刻；t(j,k)≥0，tg(j)为交叉口j的绿灯启亮时刻；t′(j,k)为第k班电车到达交叉口j的时刻。

将公式(16)带入公式(6)，继而可以重新计算电车的运行延迟时间，从而根据公式(7)～(14)可以得出经修正后的下一班次的发车时刻。

3　结语

本文以有轨电车车站断面客流量为依据，构建了一套有轨电车时刻表制订方法，主要研究成果有：将运营企业收入与有轨电车系统对乘客的服务水平两种因素量化到模型的约束条件中，使时刻表的制订兼顾上述两种因素，更加合理；通过约束条件确定发车间隔，从而得到全天发车时刻表，该方法在实践中较 已 有 研究方法更加容易执行。相对本研究，有轨电车在交叉口的等待与优先机制将是下一步研究的重点。

[1] 崔亚南.现代有轨电车应用模式及区域适用性评价研究[D].北京：北京交通大学,2012.

[2] 王庆荣,袁占亭,张秋余.基于改进遗传—模拟退火算法的公交排班优化研究[J].计算机应用研究,2012(7):2461-2463.

[3] 陈远.基于遗传算法的公交智能排班方法的研究[J].智能计算机与应用,2012(5):75-77.

[4] 李英帅,孙连超,张旭,等.基于时间客流不均衡性公交发车间隔优化方法[J].交通科技与经济,2011(6):89-92.[5] 熊桂喜,马树东.支持信号优先的快速公交行车时刻表优化算法[J].计算机与信息技术,2008(S1):12-14.

[6] 宋瑞,何世伟,杨永凯,等.公交时刻表设计与车辆运用综合优化模型[J].中国公路学报,2006(3):70-76.

[7] 覃运梅.城市公交调度优化方法研究[D].合肥：合肥工业大学,2006.

(编辑：曹雪明)

Research on Tram Dispatching Time Model Based on Passenger Flow

Ba Yuhang1Jiang Mei2Guo Zizheng1Chen Chongshuang3

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031; 2. Research Institute of Science and Technology, China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031; 3. School of Mathematics, Southwest Jiaotong University, Chengdu 611756)

Present domestic studies on the operation of public transportation dispatching time proposed very complicated algorithms and ignored the influence arising from multiple factors. Against this background, an uneven dispatching time model for tram system based on traffic flow is offered in this paper. Firstly, the model is subjected to the maximum and minimum passenger load and dispatching intervals which gives consideration to the operation company's income and the level of passenger service, then the dispatching interval is determined by the traffic flows over a station segment and the dispatching time in a whole day is worked out. Finally, the tram dispatching time model is corrected by the random fluctuations which affect tram dispatching. The method can be implemented easily compared with other methods.

tram; dispatching time; passenger flow; passenger load; dispatching interval

10.3969/j.issn.1672-6073.2016.01.010

2015-01-22

2015-04-02

巴宇航，女，硕士研究生，主要从事交通规划、交通运输安全研究，bayuhangedu@163.com

四川省科技计划项目(2014GZ0081)

U491.1

A

1672-6073(2016)01-0038-04