基于多层次模糊综合评判的自主学习能力评价系统研究与设计*

赵伟舟　景慧丽　王惠珍

(火箭军工程大学理学院　西安　710025)



基于多层次模糊综合评判的自主学习能力评价系统研究与设计*

赵伟舟景慧丽王惠珍

(火箭军工程大学理学院西安710025)

针对影响自主学习能力的因素较多和群体评价的数据量较大等问题,论文基于模糊数学理论进行了自主学习能力评价的模型研究和系统设计。首先,通过分析影响自主学习能力的主因素和子因素,建立了自主学习能力评价系统的指标体系；其次,考虑到自主学习能力评价中的不确定因素和因素集的层次关系,建立了基于多层次模糊综合评判的能力评价模型；最后根据各模块功能对评价系统进行了设计。实验表明自主学习能力评价系统能快速准确地给出评判结果并与实际情况相符。

模糊数学; 自主学习能力; 多层次模糊综合评判

Class NumberO023

1　引言

自主学习既是一种学习方法,也是一种学习习惯。它是指以学习者作为学习的主体,通过独立分析、探索、实践等方法来实现学习目标。自主学习的方法具有多样性,可以是通常意义上的查阅工具书,也可以是网络搜索获得需要的信息。自主学习的方法要求学习者在获得知识的过程中具有一些例如观察、探索、整合、实践等基本技能。自主学习能力是指具有适于自身的自主获得知识的能力,根据自主学习的不同阶段,可将自主学习能力分为学习前具有设定目标的能力,学习中具有调整方法的能力和学习后具有自我检测的能力[1～4]。

不同学习者的自主学习方法通常是不同的,但都具有一定的自主学习能力,其区别在于自主学习能力的高低或强弱。评价学员的自主学习能力就是要给出“优、中、差”方面的说明,通过了解学员的自主学习情况,给出学员自主学习能力的具体评判,可以有效调整或改进人才培养的教学模式或教学法。但是自主学习能力的评价,由于缺少没有明显的界定,难于通过具体的数值给出其确切评判。另一方面,影响自主学习的因素通常包括客观因素和主观因素以及其它不可知因素。这些原因都导致了评价某一群体自主学习能力的复杂性。模糊理论产生于十九世纪,把经典的二值逻辑转化到[0,1]逻辑上,符合人脑推理并为研究缺少明显界限的问题提供了强有力的工具[5～6]。因此,可以借助模糊数学理论研究自主学习能力的评价问题。综合评判是模糊理论中用以给出评价对象等级划分的经典方法[7～8],考虑到自主学习能力的影响因素包含主因素层和次因素层,因此可以逐层使用综合评判方法,即多层次模糊综合评判。

2　基于多层次模糊综合评判的评价模型

模糊综合评判要求对评判结果建立若干标准模式(通常称为评语集),借助模糊映射和最大隶属原则,给出评判对象对于标准模式的分类结果。这一过程需要解决三个问题: 1) 根据实际情况给出评判中的标准模式,以此作为评判所需的评语集； 2) 通过分析影响评判结果的主要因素和次要因素,建立相应的指标体系； 3) 结合各因素对评判结果的重要程度,给出评判所需的权重系数。

2.1评语集的描述

评价自主学习能力,多数情况下仅关心能力的强弱或高低,而未必希望给出某种具体的量化结果。为简单起见,这里将自主学习能力分为“优、中、差”三个等级,评价学习者的自主学习能力,即希望给出该学习者的自主学习能力属于哪一等级。

2.2建立因素集

考虑到自主学习能力主要表现在以下三个方面:即对信息的感知程度、信息理解的方法途径以及信息获得的检测效果。在信息感知方面,主要包括信息阅读、信息捕捉、兴趣驱动和知识储备等能力；在学习能力方面,主要包括信息理解、信息支配、信息搜索、知识整合等能力；在检测能力方面,主要包括信息评价、方法评价和知识检测等能力。因此评价自主学习能力可建立下面的指标体系(如表1)。

表1　自主学习能力评价指标体系

2.3权重集的建立

因素集的权重反映了各因素对评判结果的影响程度或重要程度,通常情况下,权重的分配原则是根据问题所在领域的相关理论例如层次分析法或专家系统的经验给出。考虑到感知能力、学习能力和检测能力的不同重要程度,这里设定指标权重分别为

一级指标权重:A={0.3,0.5,0.2}

二级指标权重:A1={0.3,0.2,0.2,0.3},A2={0.2,0.2,0.3,0.2},A3={0.3,0.4,0.3}

2.4多层次模糊评判

单层次模糊评判适用于仅仅具有一级指标的评判问题,多层次模糊评判适用于具有多级指标的情形。考虑到自主学习能力评价体系具有3个一级指标和11个二级指标,因此可借助多层模糊综合评判建立自主学习能力的评价模型。

Step1:获得一级指标的单因素评判矩阵

这里以一级指标“感知能力”中的“信息阅读能力”为例进行单因素评判。不妨假定有k11,k12,k13个专家认为评判对象的“信息阅读能力”U11分别为评语集中的“优、中、差”,则利用归一化方法可获得该评判对象的“信息阅读能力”属于标准模式“优、中、差”的隶属度为

(1)

按照同样方法,可获得“感知能力”中的其它三个因素:“信息捕捉能力”U12、“兴趣驱动能力”U13、“知识储备能力”U14属于标准模式的隶属度r2i,r3i,r4i(i=1,2,3)。从而对一级指标“感知能力”的单因素评判矩阵可表示为

同理,可获得一级指标“学习能力”和“检测能力”的单因素评判矩阵U2,U3。

Step2:单因素模糊评判

根据一级指标“感知能力”中各因素的权重A1与单因素评判矩阵进行合成运算,从而获得“感知能力”隶属于标准模式“优、中、差”的隶属度,即:

u1=A1U1

(2)

同理可得“学习能力”和“检测能力”的隶属度为:ui=AiUi(i=2,3),其中ui=(ui1,ui2,ui3),i=1,2,3。

Step3:模糊综合评判

由一级指标的单因素模糊评判可获得评判矩阵为

再次利用单因素评判方法可得:

D=AU={d1,d2,d3}

(3)

根据最大隶属度原则,可根据下式获得最终评判结果

i=arg{max(d1,d2,d3)}

(4)

值得注意:当di=dj(i≠j)时,采用最近距离原则获得评判结果,即:

(5)

3　多层次模糊评判系统的设计

评价学员的自主学习能力,从数据输入到评判输出其过程相当复杂,利用计算机设计应用系统能快速处理数据并获得结果[9～11]。为便于进行模糊评判系统的设计工作,可将系统分为五个基本模块,即输入模块、预处理模块、评判模块、统计模块、维护模块(如图1所示)。

3.1输入模块和预处理模块

输入模块用于输入评判阶段所需的大量数据,主要包括各专家对二级指标的评定情况,通常的输入方式包括手动录入或光电阅读。根据评价系统的指标体系,该数据可按二级指标的顺序构造成向量形式输入为x=(x1,x2,…,xn)T,这里n为评价系统的二级指标总数,xi∈{1,2,3}表示评语集“优、中、差”。

图1　自主学习能力评判系统的基本模块

3.2预处理模块

这一模块用于对输入数据进行归一化处理,以获得单因素评判矩阵中的各元素。该模块需要考虑个别专家对某评判对象打分失效的情况,此时的归一化处理仅在有效数据上进行。

3.3评判模块

这一模块主要根据前面建立的模型,获得各对象的综合评判结果并输出。在信息输出中,主要考虑两个方面:一为全体对象的评判结果,二为各评判对象一级指标的评判结果。

其流程如图2所示。

图2　评判模块流程图

3.4统计模块

该模块主要实现对某一群体人员自主学习能力评价结果的统计输出,包括“优、中、差”人数及百分比等信息,除了以数据形式输出统计结果,还可以饼状图的形式给出(如图3所示)。

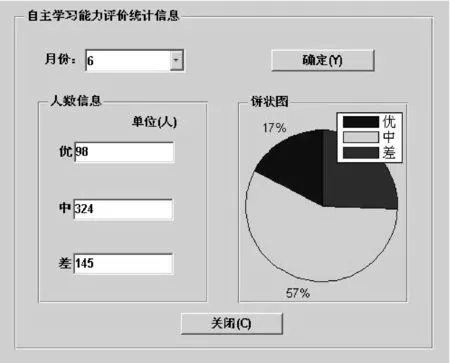
图3　评判结果的统计信息

3.5维护模块

对于自主学习评价系统,可能需要考察某一群体的自主学习能力变化情况,因此需要定期对权重集等内部数据进行更新。另外,为防止系统数据被恶意篡改,进行这些操作时需要身份验证,即管理系统时需要输入相应的用户名和密码(如图4所示),以实现一般人员的浏览功能和管理人员的更改功能。

图4　管理人员登录界面

4　结语

自主学习能力是人才培养评价的重要指标,而评价自主学习能力对于改革教学模式和教学方法具有重要作用。自主学习能力评价的复杂性源于其能力高低受多方面因素的影响,以及评判本身缺少严格的界定。借助模糊数学理论,基于多层次模糊综合评判有效实现了自主学习能力的评价,通过建立评价系统,借助计算机完成复杂的数据预处理和统计过程,能准确给出学员的评判结果,为进一步改革教学模式和人才培养方法提供指导。但是,自主学习能力评判系统仅仅粗略给出评价对象的等级划分,如果需要进行提高自主学习能力和对成绩影响的后续研究,还应当给出自主学习能力的定量评价指标,这将是进一步研究的内容。

[1] 庞维国.90年代以来国外自主学习研究的若干进展[J].心理学动态,2000(4):12-16.

PANG Weiguo. Some Progress in Foreign Autonomous Learning Research[J]. Journal of Developments in Psychology,2000(4):12-16.

[2] 庞维国.从自主学习的心理机制看自主学习能力培养的着力点[J].全球教育展望,2002,31(5):26-31.

PANG Weiguo. On the Cultivation of Autonomous Learning Ability from the Psychological Mechanism[J]. Global Education,2002,31(5):26-31.

[3] Zimmerman B.J., Risemberg R. Self-regulatory dimensions of academic learning and motivation[J]. Phye G.D. ed. Handbook of academic learning. Academic Press, 1997:105-125.

[4] Schunk D. Zmmerman B.J. Self-regulation of learning and performance[J]. Lawrence Erlbaum Associates, 1994:4-20.

[5] Zadeh L A., Fuzzy sets[J]. Information and Control,1965(8):338-353.

[6] Zadeh L A., Fuzzy logic[J]. IEEE Trans. On Control System Magazine,1988:83-93.

[7] 李海英.基于模糊数学模型的矿井巷道开拓成本决策分析[J].煤炭技术,2013,32(5):64-66.

LI Haiying. Decision Analysis of Mine Roadway Development Cost Based on Fuzzy Mathematical Model[J]. Coal Technology,2013,32(5):64-66.

[8] 李桂英.基于模糊综合评判授课质量评价系统的设计与实现[J].华南师范大学学报(自然科学版),2003(4):48-53.

LI Guiying. Design and Implementation of Teaching Quality Evaluation System Based on Fuzzy Comprehension Evaluation[J]. Journal of South China Normal University Natural(Science Edition),2003(4):48-53.

[9] 邓有林,蔡红艳.高校学报在线投稿管理系统研究与设计[J].信息与电脑,2014,12:147-149.

DENG Youlin, CAI Hongyan. Research and Design of Online Submission Management System for University Journals[J]. China Computer&Communication,2014,12:147-149.

[10] 陈静,韩月霞,张英,等.军校学员心理健康辅导系统研究与设计[J].现代计算机,2015,15(5):77-80.

CHEN Jing, HAN Yuexia, ZHANG Ying, XIE Fangfang. Research and Design of Psychological Health Counseling System of Military Academy Students. Modern Computer,2015,15(5):77-80.

[11] 李振超,陈琳,郑旭东.大数据理念下的发展性学习评价系统设计研究[J].现代教育技术,2015,25(6):108-114.

LI Zhenchao, CHEN Lin, ZHENG Xudong. Design and Research of Expansibility Learning Evaluation System in Big Data Concept[J]. Modern Educational Technology,2015,25(6):108-114.

Research and Design of Autonomous Learning Ability Evaluation System Based on Multi-level Fuzzy Comprehensive Evaluation

ZHAO WeizhouJING HuiliWANG Huizhen

(Science Institute, Rocket Army Engineering University, Xi’an710025)

Aiming at the problem of not easily evaluated autonomous learning ability for many influence factors and group data, evaluation model is researched and evaluation system is designed in this paper. Firstly, by analyzing the main factors and sub-factors, index system is built for ability evaluation. Secondly, considering the uncertain elements and the hierarchical relationship, multi-level fuzzy comprehensive evaluation model is given. Finally, evaluation system is designed according the function of every module. Experiments show the evaluation system of autonomous learning ability can rapidly supply a right result which can be in correspondence to the reality.

fuzzy math, autonomous learning ability, multi-level fuzzy comprehensive evaluation

2016年4月17日,

2016年5月23日

军队院校数学课程教学改革研究项目资助。

赵伟舟,男,硕士,讲师,研究方向：数学教育研究、信息分析与处理。景慧丽,女,硕士，讲师，研究方向：数学教育研究，最优化分析。王惠珍,女,硕士,副教授,研究方向：数学教育研究。

O023

10.3969/j.issn.1672-9722.2016.10.003