混凝土框架结构截面优化

王　琰

(武汉理工大学土木工程与建筑学院，湖北 武汉　430070)



混凝土框架结构截面优化

王琰

(武汉理工大学土木工程与建筑学院，湖北 武汉430070)

从设计变量、目标函数、约束条件三方面，提出了考虑造价和延性的框架结构多目标优化数学模型，指出该数学模型的目标函数严格基于力学与混凝土理论，约束条件依规范设定，具有精确可靠性。

框架结构，数学模型，截面尺寸，目标函数

0　引言

当今人们对建筑结构已经开始提出更多的要求，出于经济性和能源的考虑，希望造价最小；而出于安全考虑，希望结构抗震能力最大。目前结构优化时，为了确保计算的正确性、提高计算效率，我们往往借助分析软件来实现，这就需要把实际的工程问题转变成数学模型。因此本文基于以上两个优化目标的数学模型，分为设计变量、目标函数及约束条件三个部分[3]。

1　设计变量

理论上每根构件的截面尺寸都是设计变量，考虑到若每个构件的截面尺寸都不一致会造成施工的极大不便，因此可根据情况将有些变量规整成一个变量。

实际工程中梁柱的截面尺寸往往有一定模数要求，所以从理论上来说这样的设计变量是离散的。但离散变量的处理过于复杂，因此将待优化变量先看成连续型进行优化，求出最优解后再人工规整，得出最终结果。

2　目标函数

2.1分目标函数之造价

结构总造价：

C(x)=CS+CC

(1)

混凝土造价：

(2)

钢筋造价：

(3)

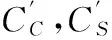
1)计算梁内钢筋时，做出以下假定：

As=ξbh0α1fc/fy

(4)

(5)

(6)

其中，ξ为相对受压区高度；αs为受弯构件截面抵抗矩系数。

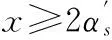
2)计算柱内钢筋时，分大偏心受压(ξ≤ξb)和小偏心受压(ξ>ξb)两种情况(见表1)：

ei=e0+ea

(7)

其中，e0为截面的初始偏心距，e0=M/N；ea为附加偏心距。

表1　柱内钢筋计算

柱长细比较大时，应考虑由构件的侧向挠度而引起的二阶弯矩的影响，利用考虑侧向挠度后的偏心距与初始偏心距的比值η把该问题考虑到计算中。

(8)

其中，ξ1=(0.5fcA)/N；ξ2=1.15-0.01l0/h；l0为构件计算长度。

2.2分目标函数之位移延性系数

用位移延性系数μ来反映结构的抗震性能：

μ=Δu/Δy

(9)

其中，Δy为结构顶点的屈服位移；Δu为结构能维持承载能力时的最大侧向挠度，且Δu=Δy+Δp，Δp为塑性阶段的水平位移 。

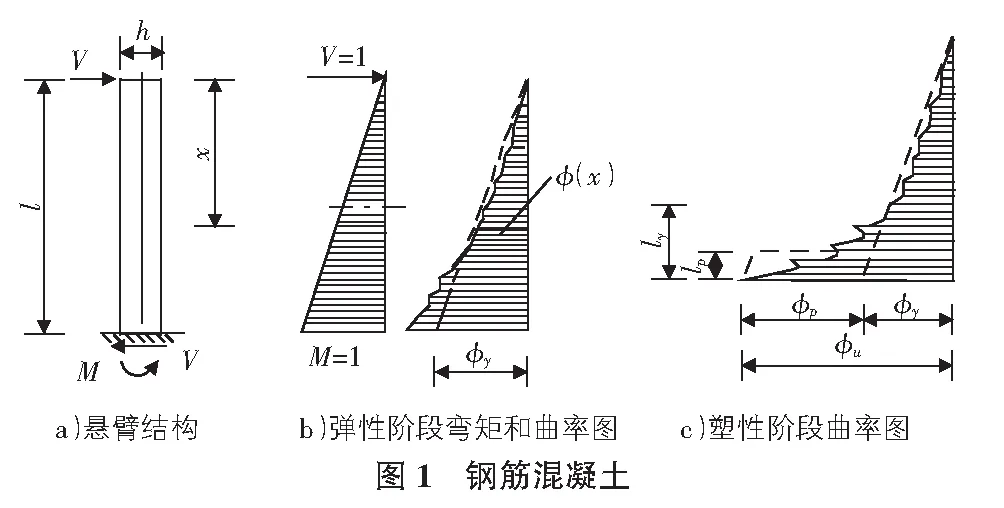
框架结构中，梁的各截面先进入屈服状态，之后梁中塑性铰处的变形会使结构产生水平位移，直至柱脚处也产生塑性铰。到结构丧失承载能力的时候，柱子的其余部分依旧保持弹性状态，结构整体的延性可以用柱子的最大侧翼挠度来体现。且柱子破坏前梁已全部失效，因此可以把柱子当成一悬臂结构去分析它的延性，简化计算。取一根长为l的构件，图1中φ(x)表示坐标为x处结构的曲率。

由图1b)中的曲率图，结构屈服时实际屈服曲率的分布可近似看成一条斜直线，沿高度用图乘法对曲率积分，得到屈服位移Δy：

Δy=∫φ(x)xdx=φyl2/3

(10)

塑性位移由塑性铰的转动能力来决定，而塑性铰的转动能力又与塑性铰区等效长度lp直接相关。图1c)中ly是构件中截面弯矩超过极限弯矩的非弹性区部分，x=ly处即是临界截面。而屈服曲率近似的斜直线与塑性阶段曲率曲线所围成的部分的面积就是塑性铰区产生的塑性转角θp，用等效矩形计算，φu-φy是矩形的宽度，lp是其高度，也是塑性铰的等效长度。关于等效长度目前有多种经验公式，其中Paulay提出的式(11)是我国《公路桥梁抗震设计细则》和美国Caltrans规范中计算lp的公式的基础[4]，其中，ds为钢筋直径。

lp=0.08l+0.22dsfy

(11)

θp=φplp=(φu-φy)lp

(12)

Δp=θp(l-0.5lp)=(φu-φy)lp(l-0.5lp)

(13)

引入截面曲率延性系数：

μφ=φu/φy

(14)

其中，φy为钢筋屈服时的截面曲率；φu为构件破坏时的截面曲率。

Δu=Δy+Δp=φyl2/3+(φu+φy)/lp(1-0.5lp)

(15)

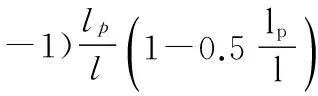
(16)

对钢筋混凝土适筋受弯截面进行全过程受力分析时是基于平面假定的原则和以力的平衡方程作为计算原理的。

图2为适筋截面受拉钢筋开始屈服和截面达到最大承载力时的应力、应变图。

由图2中的应变图：

φy=εy/(1-k)h0

(17)

φu=εcu/xn

(18)

则截面曲率延性系数：

(19)

其中，εcu为混凝土的极限压应变；εy为受拉钢筋的屈服应变；xn为Mu下受压区高度。

受压区混凝土的应力图可用等效矩形来替代，等效矩形的高度是x=β1xn，宽度是α1fc，由力的平衡方程：

xn=x/β1=(ρ-ρ′)fyh0/β1α1fc

(20)

受拉钢筋开始屈服时受压区高度系数k可按图2a)中的三角应力图，根据平衡条件计算。对于双筋截面：

(21)

2.3总的目标函数

因为C(x)越小而μ(x)越大越好，于是将多目标问题用乘除法变成单目标问题，构造目标函数F(x)，优化目标是它尽可能小：

F(x)=C(x)/μ(x)

(22)

3　约束条件[1,2]

3.1框架梁的约束条件

1)有关抗震构造的约束条件。

a.最小截面尺寸：只要构件截面尺寸不太小就可有效防止斜压破坏的发生，当hw/b≤4时：

Vb≤(0.20βcfcbh0)/γRE

(23)

b.截面尺寸：b≥200 mm，为避免梁侧挠度过大而失稳：h/b≤4。

c.配筋率：梁纵向钢筋配筋率ρmin≤ρ≤ρmax=5.0%。

2)有关强度的约束条件。

a.梁正截面抗弯承载力：为了充分考虑材料的作用，按双筋梁来验算梁正截面强度：

Mb≤α1fcbx(h0-x/2)+fy′As′(h0-as′)

(24)

b.梁斜截面抗剪承载力:对于一般梁:

Vb≤(0.6×0.7ftbh0+fyvAsvh0/x)/γRE

(25)

3.2框架柱的约束条件

1)有关抗震构造的约束条件。

a.轴压比：

μc=N/fcbh≤[μc]

(26)

b.最小截面尺寸验算：

Vc≤(0.20βcfcbh0)/γRE

(27)

c.截面约束：b≥300 mm；Hn/h≥4。

d.配筋率约束：柱纵向配筋率ρmin≤ρ≤5%，且每侧纵向配筋率不小于0.2%。

2)有关强度的约束条件。

对柱斜截面抗剪承载力进行验算：

a.柱轴力N为压力时：

(28)

其中，N为考虑地震作用组合的框架柱轴向压力设计值，且N≤0.3fcA。

b.柱轴力N为拉力时：

(29)

其中，N为考虑地震作用的柱轴向拉力设计值。式(29)右边括号内的计算值要不小于fyvAsvh0/s，且fyvAsvh0/s≥0.36ftbh0。

3.3整体结构约束条件

1)层间位移角约束：对框架结构，层间最大位移Δu与层高h之比不大于1/550。 2)受压区高度约束：在考虑延性设计时，一级抗震下：x≤0.25h0；二、三级抗震下：x≤0.35h0。

4　结语

以上已用截面尺寸表示出目标函数以及待约束的各种物理量，根据这样的数学模型我们便能利用诸如ANSYS这样的有限元分析软件进行结构建模、定义设计变量，将目标函数和约束条件的数学公式转换成计算机语言，最终进行计算得到结果。此数学模型的目标函数是严格基于力学与混凝土理论，约束条件参照规范来设定，因此该数学模型精确可靠，在实际工程的运用中也能发挥作用。

[1]GB 50010—2010，混凝土结构设计规范[S].

[2]GB 50011—2010，建筑抗震设计规范[S].

[3]汪树玉，杨德铨，刘华国，等.优化原理方法与工程应用[M].杭州：浙江大学出版社，1991.

[4]孙治国，王东升，郭迅，等.钢筋混凝土墩柱等效塑性铰长度研究[J].中国公路学报，2011(10)：107-108.

On section optimization of concrete framework structure

Wang Yan

(CivilEngineeringandArchitectureCollege,WuhanUniversityofTechnology,Wuhan430070,China)

From the design variation, objective function, and constraint conditions, the paper points out the multiple optimal mathematic models with the consideration of cost and ductility, and points out the objective function of the mathematic model can be designed for the dynamics and concrete theoretic constraint conditions, so it has accurate reliability.

framework structure, mathematic model, section size, objective function

1009-6825(2016)08-0040-03

2016-01-08

王琰(1992- )，女，在读硕士

TU375.4

A