改进型倍压Boost PFC变换器的MCM控制算法研究

许培德

(1. 福州大学, 福州 350108; 2. 福建水利电力职业技术学院, 福建 永安 366000 )

改进型倍压Boost PFC变换器的MCM控制算法研究

许培德

(1. 福州大学, 福州 350108; 2. 福建水利电力职业技术学院, 福建 永安 366000 )

普通的倍压Boost PFC变换器因具有输入电流连续、电磁干扰小等优点而作为半桥逆变器的前端得到广泛运用, 但其拓扑的开关管和电感在工频周期内未得到充分利用. 本文针对普通倍压Boost PFC变换器的缺点提出一种改进型倍压Boost PFC变换器, 同时引入混合导通模式控制算法控制此新型变换器, 有效地降低了输入电流的畸变率(THDi), 使系统在全功率范围内均能得到一个较好的PFC效果. 最后搭建1kW的改进型倍压Boost PFC试验样机, 并在该平台上验证了混合导通模式控制算法的可行性.

功率因数校正; 混合导通模式; 倍压型

引言

Boost型拓扑在功率因数校正中因其电流连续、电磁干扰小而得到广泛使用[1～6], 根据其电感电流的工作情况可分为三种不同的导通模式: 断续导通模式(Discontinuous Current Mode, 简称DCM)、连续导通模式(Continuous Current Mode, 简称CCM)、临界导通模式(Critical Conduction Mode, 简称CRM), 相对应的控制法[7～10]为DCM控制法、CCM控制法、CRM控制法. 当输出固定负载时, Boost PFC拓扑可根据其输出功率的大小选择电感电流工作的模式, 设计电感, 并选择相对应的控制算法. 而对于输出负载不断变化的Boost PFC(比如说UPS), 输入电流在跟踪输入市电电压时, 无法保证在工频周期内其升压电感都工作在连续导通模式或者是断续导通模式, 此时电感时而工作在断续导通模式, 时而工作在连续导通模式, 即混合导通模式(Mixed Conduction Mode, 简称MCM), 相对应的控制方法为混合导通模式(MCM)控制法.

Boost PFC主要用在全桥逆变器或后级直接加阻性负载中; 在输出交流电相同情况之下, 全桥逆变器负载的输入端母线电压仅为半桥逆变器的50%. 当其处于运行状态时, 考虑到Boost电路升压变比不能随意变化, 这就会导致只包含一个Boost的PFC电路无法满足半桥逆变器输入母线电压的需求, 要解决这一问题, 可以在PFC电路中另外再增加一个Boost, 从而构成倍压Boost PFC变换器, 产生正负母线电压, 满足半桥逆变器负载及电源输入端的要求.

笔者重点分析了一般性Boost PFC变换器的运行模式, 分析结果表明, 这种拓扑的电感以及开关管还有简化的空间, 经过进一步的简化能够创造全新的倍压Boost PFC变换器. 笔者采用对比分析的方法, 以一般的倍压Boost PFC变换器为标准, 比较、提炼出新型倍压Boost PFC变换器的优势之所在. 其次详细介绍了MCM控制的此新型变换器的思路, 最后搭建试验样机, 试验平台验证了MCM控制的改进型倍压Boost PFC变换器的可行性.

1　拓扑电路原理

图1为一般的倍压型Boost PFC带半桥逆变器拓扑. 在实践中, 若大电网进入到正半周期的话, SCR1就会连通, T1、D1以及L1所形成的Boost PFC电路中就会出现正母线电压(图2(a)). 若大电网切换到负半周期的话, SCR2就会连通, T2、D2以及L2所形成的Boost PFC电路中就会出现负母线电压(图2(b)).

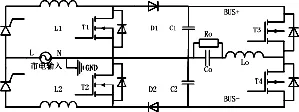
图1　普通的倍压Boost PFC和半桥逆变器

对图2进行分析可知, 在大电网完整周期内, 我们可以将一般的倍压Boost PFC当做两个彼此互不影响的Boost PFC电路, 这种变换器的缺点在于电感以及开关管并没有得到最大程度的利用. 例如, 在大电网处于正半波时, 电感L1以及开关管T1就会运行, 但此时L2和T2并未运行, 而在负半波状态下, 则出现完全相反的运行情况. 这充分说明, 在一般的倍压Boost PFC中, 有将近一半的核心零部件未能在最大程度上发挥作用.

图2 普通倍压型Boost PFC在一个工频周期内的等效电路

图3为经过改良后的倍压Boost PFC带半桥逆变器拓扑. 当大电网处于正半周期时, 包含SCR1、SCR4、L、T以及D1的Boost PFC电路中就会出现正母线电压. 当大电网处于负半周期时, 包含SCR2、SCR3、L、T以及D2的Boost PFC电路中就会出现负母线电压. 和一般的倍压Boost PFC对比来看, 无论是在哪一个半周期内, 电感和开关管都能发挥应有的作用, 有效提升了零部件的利用率.

图3　改进型倍压Boost PFC和半桥逆变器

2　MCM控制原理

这里以Boost PFC变换器为例分析MCM控制算法. 假设电感工作在连续导通模式, 其对应的CCM算法[7～9]推导过程如下:

在一个开关周期内Boost变换器升压电感L所承受的平均电压

其中ΔI为电感电流变化, ΔT为时间变化.

用在DC/DC变换场合的Boost变换电路在稳定的情况下, ΔI基本上接近于0, 电压L承受的平均电压VL也接近于0. 而对于应用在功率因数校正电路的Boost变换器, 在稳定的情况下其输入电流iin跟踪输入市电电压vin, 当ΔT为开关周期Ts时, ΔI表示的是电流参考值iref与实际开关周期的电流值iL(t)之间的差值, 可表示为

工作在连续导通模式下的Boost PFC变换器, 升压电感在一个开关周期内所承受的平均电压VL由两部分组成: 开关管导通期间电感两端电压为市电输入电压vin, 开关管关断期间电感两端电压为反向的Vo-vin(其中Vo为输出端电压). 因而VL可表示为

其中D为开关管的占空比.

结合式(1)和式(3)可得到连续导通模式下的占空比D的表达式为

仍以Boost PFC变换器为例, 假设电感工作在断续导通模式, 其对应的DCM算法推导过程如下:

稳态下, 断续导通模式输入、输出的变压比[10]为:

其中Io为母线电流有效值.

理论上, 输入功率等于输出功率, 因此Po=VinIin. 半个工频周期电感电流的瞬时值为

依据式(7)和式(8)可得到占空比D的表达式为

MCM控制算结合了DCM、CCM算法. 在两种算法的选择上, 由采用的控制芯片分别计算出DCM、CCM各自算法的占空比, 选择较小者输出驱动开关管.

图5为MCM控制的改进型倍压Boost PFC变换器的系统控制框图.

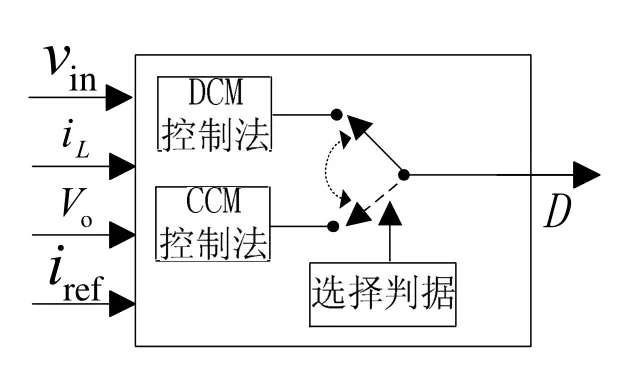
图4　MCM算法控制图

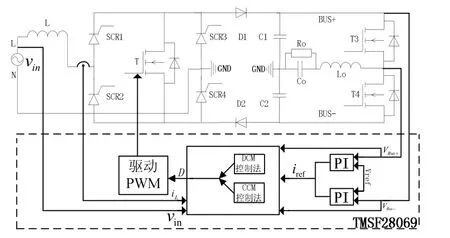
图5　系统控制框图

3　试验验证

为验证MCM控制的改进型倍压Boost PFC变换器的可行性, 搭建实验平台进行验证. 主电路(如图3所示)参数: 输入市电电压范围120～260V; 输入频率44Hz～54Hz; 开关频率20KHZ; 输出电压正负360V;升压电感2mH; 额定功率1000W. 控制芯片采用TI公司的 TMS320F28069. 图6为在输入市电电压 220V下负载为1000W时的市电输入电压、电流波形. 表1为在功率分别在200W、500W、1000W下的PF值和THDi值. 由图6和表1可知输入电流能很好的跟踪输入电压, 具有高PF值、低THDi的优点.

表1　实验结果

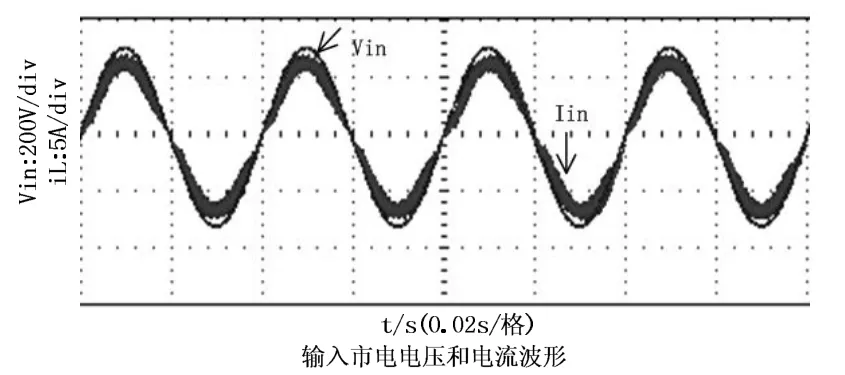
图6　市电电压、电流波形

4　结束语

本文所搭建的改进型倍压Boost PFC变换器试验样机在实现与倍压Boost PFC变换器相同功率因数校正之目的的同时, 省略了一个电感和开关管, 器件成本降低; 利用MCM控制法对改进型倍压Boost PFC变换器进行控制, 并在试验样机上验证了MCM控制的改进型倍压Boost PFC变换器的具有PF值高、低THDi的优点.

[1] Colin W Clark, Fariborz Musavi, Wilson Eberle. Digital DCM detection and mixed conduction mode control for Boost PFC converters[C]. IEEE APEC, California, 2012: 1～15

[2] 陆治国, 马雪峰, 许 黎, 等. 一种改进的单相无桥功率因数校正器[J]. 电力电子技术, 2010, 44(7): 20～21

[3] Raphael A Da Camara,Paulo P Praca,Cicero M T Cruz,et al.Voltage doubler boost rectifier based on three-state switching cell for UPS application [C]. 35th Annual IEEE Industrial Electronics Conference, 2009: 950～955

[4] 于海坤, 许建平, 张 斐, 等. 具有宽负载范围的新型Boost功率因数校正器[J]. 电工技术学报, 2011, 26(12): 93～98

[5] Rene P T Bascope,Luiz D S Bezerra,Carlos G C Branco. A Step-up DC-DC Converter for Non-Isolated On-Line UPS Application[C]. IEEE ISIE, Italy, 2010: 602～607.

[6] A Karaarslan,I Iskender. Average sliding control method applied on power factor correction converter for decreasing input current total harmonic distortion using digital signal processor [J]. IET Power Electron. 2012.5(5): 617～626

[7] 吴丽华, 郭伟光, 王旭东, 等. 一种用于数控功率因数校正的占空比控制算法[J]. 电机与控制学报, 2010, 14(3): 92～96

[8] K. D. Gusseme, D.M. Van de Sype. A. P. M. Van den Bossche, and J. A. Melkebeek. Digitally controlled boost power-factor-correction converters operating in both continuous and discontinuous conduction mode[J]. IEEE Trans. Ind. Electron., 2005, 52(1): 88～97

[9] 叶满园. 预测平均电流控制Boost PFC变换电路[J]. 华东交通大学学报, 2011, 28(2): 24～28

[10] 姚 凯, 阮新波, 冒小晶, 等. 电流断续模式Boost功率因数校正变换器的变占空比控制[J]. 电工技术学报, 2011, 26(11): 14～24

Algorithm of MCM Applied in a Modified Voltage Doubler Boost PFC

XU Pei-de
(1. Fuzhou University, fuzhou 350108, China; 2. Fujian College of Water Conservancy and Electrical Power, Yong’an 366000, China)

Because of the continuous input current and small electromagnetic interference, conventional voltage doubler Boost PFC converter has been widely applied in the front-end stage of half-bridge inverter. But this conventional converter is not taking full advantage of its switches and inductances. A modified voltage doubler Boost PFC is presented in this paper aiming to make up the shortfall. Besides, the Mixed Conduction Mode Algorithm is adopted to improve the quality of the input current of the novel converter, and a good result is obtained during the full power range. Finally, a 1KW experimental prototype is set up to verify the feasibility of the MCM Algorithm.

power factor correction; mixed conduction mode; voltage doubler

TM46

A

1672-5298(2016)03-0031-04

2016-05-23

许培德(1984- ), 男, 福建永春人, 福州大学硕士研究生. 主要研究方向: 电力电子技术与电力系统自动装置