非线性扰动Schrodinger方程的低正则性问题
2016-11-05张再云周小强丁卫平甘向阳胡满佳
张再云, 周小强, 丁卫平, 甘向阳, 何 帆, 胡满佳
(湖南理工学院 数学学院, 湖南 岳阳 414006)
非线性扰动Schrodinger方程的低正则性问题
张再云, 周小强, 丁卫平, 甘向阳, 何 帆, 胡满佳
(湖南理工学院 数学学院, 湖南 岳阳 414006)
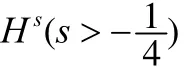
非线性扰动Schrodinger方程; Fourier限制模方法; 压缩映射原理; 局部适定性
引言
考虑带有Kerr law非线性项的非线性扰动Schrodinger方程
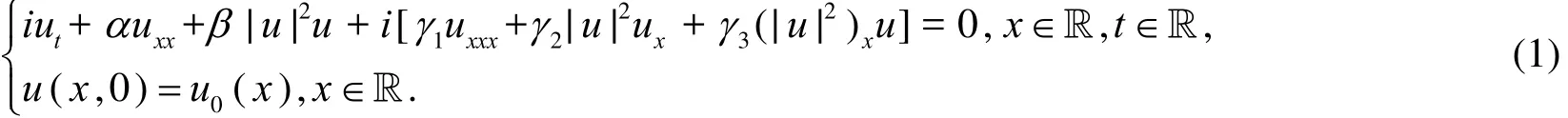
(Ⅰ) 非线性 Schrodinger 方程:
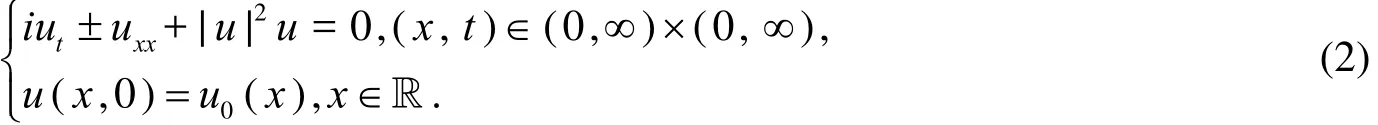
(Ⅱ) 含有导数项的非线性 Schrodinger 方程:
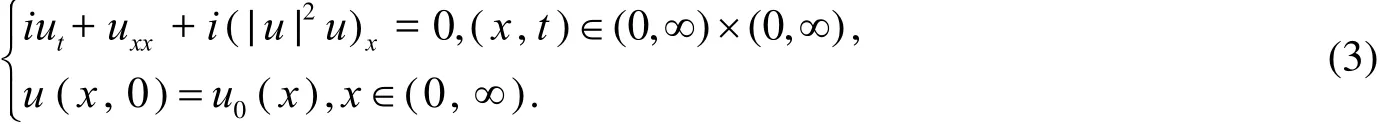

1 主要结果
2 三线性估计
本节将利用Fourier限制模方法建立三线性估计, 然后得到(1)的局部适定性. 为此, 需给出一些基本引理. 首先引入符号:

3 主要结果的证明

[1] Zai Yun Zhang, Zhen Hai Liu, Xiu Jin Miao and Yue Zhong Chen. New exact solutions to the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J]. Appl. Math. Comput, 2010(216): 3064~3072
[2] Zaiyun Zhang, Jianhua Huang,Well-posedness and unique continuation property for the generalized Ostrovsky equation with low regularity[J].Math. Meth. Appl. Sci, 2016(39): 2488~2513
[3] Y. Tsutsumi, L2-solutions for nonlinear Schrodinger equations and nonlinear groups[J]. Funkcial. Ekvac, 1987(30): 115~125
[4] H. Takaoka, Well-posedness for the one dimensional Schrodinger equation with the derivative nonlinearity[J].Adv. Diff. Eq, 1999(4): 561~680
[5] C. E. Kenig, G. Ponce, L. Vega, On the support of solutions to the generalized KdV equation[J].Ann. Inst. H. Poincare Anal. Non Lineaire, 2002(19):191~208
[6] T. Ozawa, Y. Tsutsumi, Space-time estimates for null gauge forms and nonlinear Schrodinger equations[J].Diff. Integ. Eqs, 1998(11): 201~222.
[7] B. L. Guo, S. B. Tan, Global smooth solution for nonlinear evolution of Hirota type[J].Science in China, Ser. A, 1992(35): 1425~1433
[8] 张再云. 非线性色散波方程的低正则性问题[D]. 国防科技大学博士后出站报告, 2015
Low Regularity for the Perturbed Nonlinear Schrodinger's Equation with Kerr Law Nonlinearity
ZHANG Zai-yun , ZHOU Xiao-qiang, DING Wei-ping, GAN Xiang-yang, HE Fan, HU Man-jia
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)
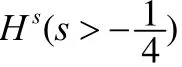
the perturbed Schrodinger's equation; Fourier restriction norm method; contracting mapping principle; local wellposedness
O175.29
A
1672-5298(2016)03-0001-03
2016-07-21
湖南省自然科学基金项目(2016JJ2061); 湖南省教育厅优秀青年项目(15B102); 中国博士后科学基金特别资助项目(2014T70991); 中国博士后科学基金面上项目(2013M532169)
张再云(1975- ), 男, 湖南宁乡人, 博士, 湖南理工学院数学学院副教授. 主要研究方向: 应用数学
