基于改进混合粒子群优化的特定谐波消除脉宽调制策略
2016-11-05陈玉健
陈 炜,陈玉健,耿 强
(1. 天津大学电气与自动化工程学院,天津 300072;2. 天津工业大学电工电能新技术天津市重点实验室,天津 300387)
基于改进混合粒子群优化的特定谐波消除脉宽调制策略
陈 炜1,陈玉健1,耿 强2
(1. 天津大学电气与自动化工程学院,天津 300072;2. 天津工业大学电工电能新技术天津市重点实验室,天津 300387)
针对传统迭代法求解特定谐波消除脉宽调制策略(SHEPWM)开关角方程组需要合适的初值和难收敛的问题,提出一种改进的混合粒子群优化(HPSO)算法对其进行求解.该算法对粒子群(PSO)算法的权重系数和学习因子进行了改进,并且提出了一种温度系数线性递减的模拟退火(SA)算法与粒子群算法结合,有效弥补了传统粒子群(CPSO)算法求解开关角收敛速度慢和精度低的缺点.仿真分析表明,该算法消除了对初值的依赖,提升了算法寻优的能力,从而提高了求解速度与精度,并且通过实验验证了该算法的可行性.
特定谐波消除;优化算法;模拟退火;混合粒子群优化
在机车牵引、风力发电等大功率系统中,受到开关损耗和散热的限制,功率器件的开关频率较低.但是,传统的调制策略在开关频率与输出电压频率之比较小的情况下会产生大量的低次谐波,严重影响系统的运行性能[1].
特定谐波消除脉宽调制策略(selective harmonic elimination pulse width modulation,SHEPWM)在功率器件开关频率较低的情况下能够有效消除低次谐波,提高逆变器输出的波形质量和直流电压利用率,适合作为大功率逆变器系统的调制策略[1].但是,该策略的开关角求解方程是傅里叶分析产生的非线性超越方程组,求解困难,所以开关角的求解成为学者研究SHEPWM的重点和难点.
为了求解方程,应用较多的是牛顿迭代法,该方法在初值合适的情况下能够有效求解开关角[2-3].文献[4]使用同伦算法对迭代法进行改进,增强了迭代算法收敛的能力.文献[5]提出了基于Walsh方程的求解方法,降低了算法对初值的要求.上述方法求解时都需要合适的初值,并且随着求解开关角的增多,算法复杂性增加,加大了求解的难度.通过研究发现,开关角的求解问题可以转化成为最优化问题来解决,这有利于摆脱求解初值的束缚,得到更优求解方法[6-7].文献[8]和文献[9]分别采用了混合遗传算法和传统粒子群优化(conventional particle swarm optimization,CPSO)算法对电压加权总谐波畸变率和电压总谐波畸变率最小时的开关角进行优化求解,减小了输出电压的总谐波畸变率.文献[10]用蚁群算法对开关角方程进行求解,有效提高了求解精度.文献[11]提出了蜂群算法用于多电平逆变器开关角求解.从上述研究可以发现,群优化算法适合于求解SHEPWM开关角方程.
在群优化算法中,粒子群优化算法因其思想直观、实现简单并且具有很高的执行效率成为研究热点,但粒子群算法易陷入局部最优解[12-13].为提高算法的性能,文献[14]采用随迭代次数线性递减的惯性权重,使得算法前期具有较高的全局搜索能力,后期具有较高的局部搜索能力,加快了收敛速度;在此基础上,文献[15]采用模糊调整权重法动态调节全局和局部搜索能力.文献[16]将模拟退火(simulated annealing,SA)算法引入到了粒子群算法中,使搜索过程具有概率跳变的能力,增强了算法寻优的能力.
本文提出一种改进的混合粒子群优化(hybrid particle swarm optimization,HPSO)算法,并将其应用于SHEPWM开关角的求解.该算法对粒子群算法的权重系数和学习因子进行改进,并且将温度系数随迭代次数递减的SA算法与PSO算法结合来提升算法寻优的能力.本文对改进算法的性能和该算法求解的结果进行分析,通过实验验证求解结果的有效性.
1 SHEPWM开关角求解方程
对于两电平三相逆变器,当采用双极性PWM调制方式时,产生的输出相电压有正电平开始和负电平开始两种形式,分别称为a类和b类,其中a类波形在1/4周期内开关角的个数N为偶数,b类为奇数.图1为a相双极性调制PWM输出波形,a类以N=2为例,b类以N=3为例.图1所示α1、α2、α3为开关器件切换时刻的相位角,简称为开关角.
对逆变器输出的相电压波形进行傅里叶级数展开,其表达式为

式中:n为谐波次数;ω为基波角频率.
由于输出电压存在1/4周期对称性和半波对称性,所以Bn=0,An可以用1/4周期中的开关角α1,α2,…,αN表示,即
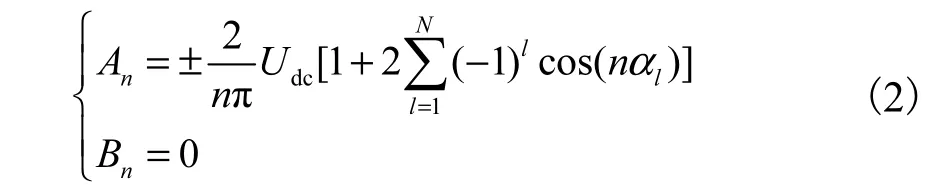
式中:l为开关角编号;N为1/4周期内开关角的个数;Udc为逆变器输入侧的直流电压;“+”用于a类波形的计算;“-”用于b类波形的计算.
定义调制比为

式中U1为参考电压.
在三相逆变器中,由于波形存在三相对称、半波对称和1/4周期对称,在输出的线电压中3及3的倍数次谐波和偶数次谐波为零.令基波幅值等于参考电压,指定次数的谐波幅值为零,即可得到SHEPWM的开关角度求解方程组为

式中q为要消除谐波的次数,q=5,7,…,3,g±1(g为偶数).求解N个开关角需要N个方程,式(4)中只需取N-1个q值即可,即此时能消除N-1个不同次数的谐波.
式(4)为多变量的非线性超越方程组,并且存在多组解,其求解比较困难.为求解此方程组,可将其转换成为最优化问题,即

式中0<α1<α2<…<αN<π/2.
求解F(α1,…,αN)的最小值,该最小值所对应的开关角就是式(4)所表示的开关角方程组的解.本文将F(α1,…,αN)定义为算法的适应度函数,采用改进的混合粒子群优化算法进行最优化求解.
2 基于改进混合粒子群算法的开关角求解
2.1自适应调节的权重系数和学习因子
在CPSO中,每个粒子都有位置、速度和由目标函数决定的适应度值,并根据“自身经验”和“种群经验”在搜索空间中向更好的位置移动,搜索全局最优解.CPSO中的各系数均为常数,其算法更新方程为

式中:k为当前迭代次数;i为粒子编号(i=1,2,…,s,s为群体规模);为第i个粒子的位置,,即第i组开关角的值;为第i个粒子的速度,即第i组开关角的速度,为第i个粒子的最优点,即第i组开关角自身迭代的最优值,即s组开关角中的最优值,为全局最优点,为惯性权重;c1和c2为学习因子;r1和r2为(0,1)之间的随机数.
在CPSO中,由于惯性权重w和学习因子c1、c2都是常数,算法不能根据具体情况动态调整,寻优的性能下降,所以需要算法的参数w、c1、c2随迭代次数的增加动态调整.
在求解SHEPWM方程组时,根据方程组的特点,当开关角的适应度值较大时,惯性权重系数w应该较大,以保证搜索的全局性;而当开关角的适应度值较小时,惯性权重系数w应该较小,以保证在该粒子处搜索的精确性.因此,惯性权重的选取应根据开关角的适应度值大小进行自适应选择.
为了动态地调节算法的局部和全局搜索的能力,定义惯性权重系数为

式中:wmin和wmax分别为惯性权重的最小值和最大值;Fi为第i个粒子的适应度值;Favg为当前所有粒子适应度的平均值;Fmin为当前所有粒子适应度的最小值.
为了进一步提高算法性能,对学习因子也进行改进,通过使两个因子分别变化,使算法在优化的初始阶段具有较大的自我学习能力和较小的社会学习能力,加强全局搜索能力;而在后期则刚好相反,有利于收敛到全局最优解.
为此,定义两个学习因子分别为

式中:c10和c20分别为c1和c2的迭代初值;c11和c21分别为c1和c2的迭代终值;k和kmax分别表示当前迭代次数和最大迭代次数.
2.2改进的模拟退火混合粒子群算法
CPSO算法本身不具备粒子跳变的能力,使粒子容易在局部最优解处停滞.本文将模拟退火思想引入到粒子群算法中,使得算法在整个搜索过程中具有概率跳变的能力.传统的退火方式温度系数设置为常数,本文提出了温度系数随迭代次数的增加而线性递减的退火策略,保证迭代开始时,温度系数较大,保证搜索的全局性;而迭代后期温度系数较小,缩短收敛时间.
假设模拟退火算法的初始温度系数和最终温度系数分别为t0和t1,则第k次迭代时的温度可表示为

当前温度下突变的概率可以表示为

后文中将改进的自适应权重系数和学习因子的模拟退火粒子群算法简称为改进的混合粒子群算法.图2为本文提出的改进混合粒子群算法的流程.
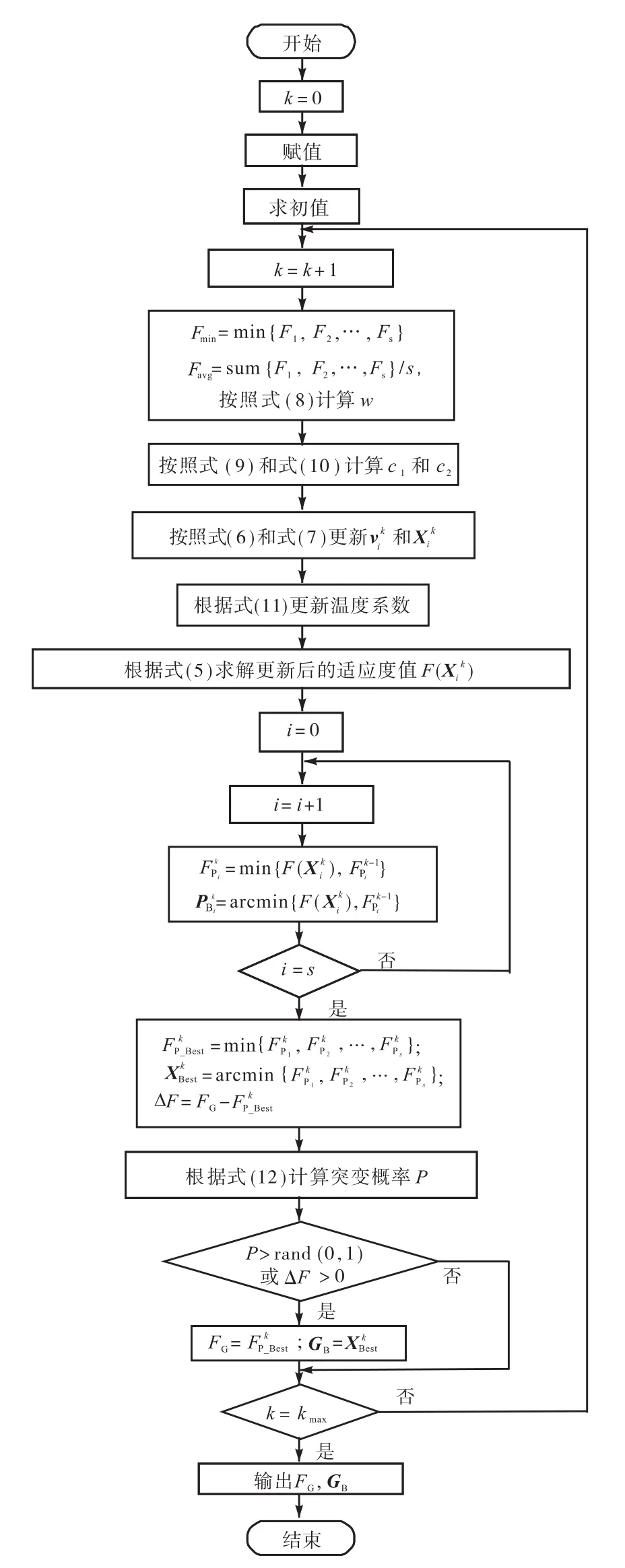
图2 改进混合粒子群算法优化流程Fig.2 Flow chart of the improved HPSO algorithm
迭代开始时,需赋值的参数有最大迭代次数kmax,种群规模s,权重系数wmin和wmax,学习因子c10、c11、c20、c21,温度系数t0和t1.为了使退火算法从初始温度逐渐下降,温度系数应在(0,1)范围内,设置t0=1,使算法从初始温度开始降温,设置t1=1× 10-3使温度系数线性递减,提升降温过程的速度.设初始温度T0=1.赋值给粒子极限速度vmax=0.05,π.
求取初值的步骤为:首先在(0,π/2)之间随机选取开关角在之间随机选取初始速度然后,根据式(5)计算出各组初始开关角的适应度值并且根据定义计算初始个体最优粒子为初始个体最优粒子的适应度值为初始个体最优粒子的适应度最小值为初始个体最优粒子中适应度值最小的粒子为最后,求解初始全局最优粒子的适应度值为初始全局最优粒子为
在改进的HPSO算法的迭代过程中,对于第i个粒子,如果当前迭代次数下的值优于个体最优值时,就使替代即个体最优的适应度值个体最优表示和中适应度较小的那个.此时,表示第k次迭代时s个个体最优粒子的最小适应度值,表示第k次迭代时s个个体最优粒子中适应度值最小的粒子.
在更新全局最优GB时,当计算得到的ΔF>0时,以概率1接受而当ΔF<0时,以概率P接受此时全局最优粒子以概率P发生跳变,使算法具有一定接受较差解的能力,提高了算法全局搜索的能力.
采用改进的退火算法不但能够提高改进算法的执行速度,同时随着迭代次数增加,P逐渐减小,在迭代初期P值较大,保证了在搜索初期粒子以较大概率接受差解,有利于跳出局部最优;到迭代后期,P值较小,算法接受较差解的概率较小,粒子能在某个局部空间进行细致搜索.
2.3改进的HPSO算法的求解结果
本文采用改进的混合粒子群算法分别对1/4周期含有2、3、5、7、9个开关角的情况进行求解,其中既包含a类波形(N=2),也包含b类波形(N=3,5,7,9).每种情况下求得的解各两组,结果如图3所示,实线为第1组,虚线为第2组.

图3 改进混合粒子群优化算法求解结果Fig.3 Results of the improved HPSO algorithm
对于本文求解的SHEPWM优化问题,混和粒子群算法求得的两组开关角均是最优解,均能消除指定次谐波,达到消谐目的.消除指定次数的谐波之后,还存在的主要谐波含量是最低的两次不为零的谐波.为了研究调制策略的电压谐波特性,可以使用电压谐波畸变因数(harmonic distortion factor,HDF)[6]来进行评价,定义此因数为

式中U3N+1、U3N+5、U3N+2、U3N+4分别为3N+1、3N+ 5、3N+2、3N+4次谐波幅值.
将在各个调制比m下的开关角代入到谐波计算表达式(2)中即可得到消谐之后剩余的最低两次谐波的含量,利用式(13)可以计算出不同N时,在求得的两组开关角作用下输出电压的HDF,图4为HDF随m变化的曲线.
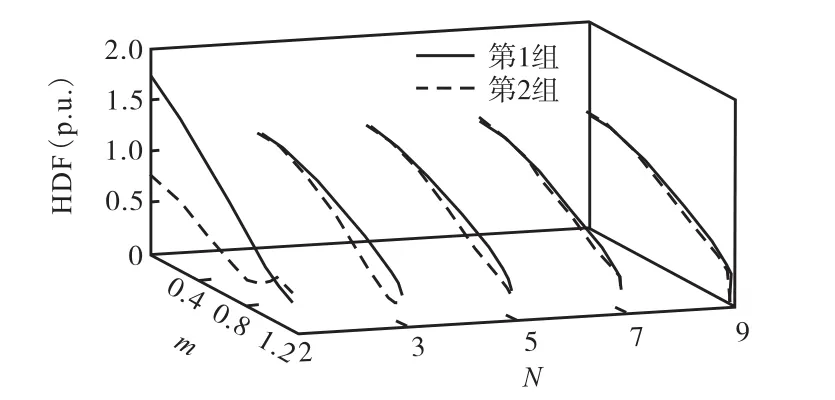
图4 两组解的HDF对比Fig.4 Comparison of HDF between two sets of solutions
从图4中两组开关角作用下输出电压的电压谐波的HDF来看,第2组开关角作用下的特性要好于第1组开关角,并且两组开关角作用下的特性差距随着开关角数目的增多而逐渐减小.
3 改进混合粒子群算法分析
为了验证本文所提算法的性能,以m=0.6时求解两个开关角为例,对传统粒子群(CPSO)、惯性权重线性变化粒子群(LPSO)、传统模拟退火粒子群(SAPSO)算法与改进的混合粒子群(HPSO)算法的求解过程进行了比较,各粒子群算法参数如表1所示,比较结果如图5所示.
从图5可以看出,CPSO陷入了局部最优解;LPSO收敛时迭代次数较少,收敛时适应度值较小,说明求解角度精度比CPSO高;SAPSO求解的精度高于LPSO和CPSO,但是其收敛时迭代次数较多;而本文采用的HPSO则在求解到最优解的同时,保证了算法以最少的迭代次数收敛.

表1 不同粒子群优化算法参数Tab.1 Parameters of different PSO algorithms
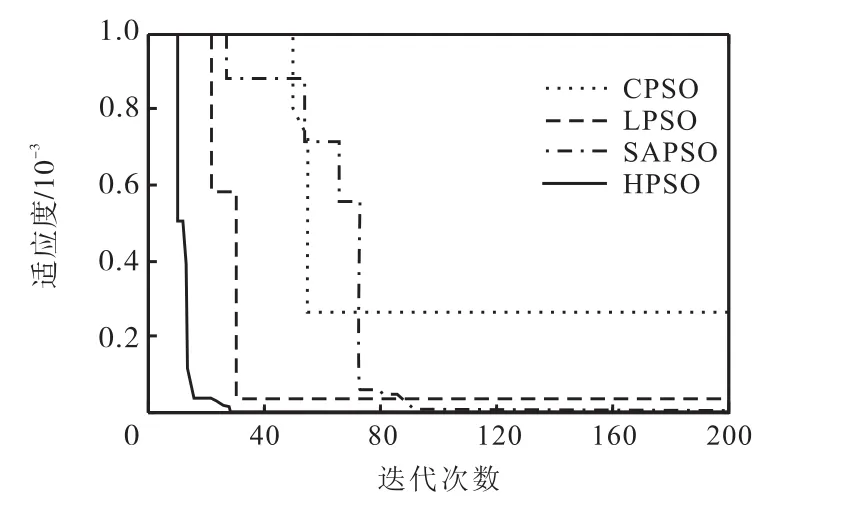
图5 不同粒子群算法求解过程对比Fig.5 Comparison of solving process of different PSO algorithms
为了进一步验证算法的优越性,在相同条件下对牛顿迭代法和各种粒子群算法进行性能对比分析.以m=0.6时求解两个开关角为例,在随机初值的情况下对迭代法和各种粒子群算法均运行20次,对平均单次迭代耗时、收敛时平均迭代次数、收敛时平均总体迭代耗时以及平均适应度值进行对比分析,结果如表2所示.

表2 不同算法性能对比Tab.2 Comparison of performance of different algorithms
从表2可以看出,采用牛顿迭代法时,赋与粒子群算法同样(0,π/2)之间的随机初值,算法不收敛,而粒子群算法则都能收敛,但不同粒子群算法收敛性能不同.由于本文的HPSO算法改进了w、c1、c2,并加入改进SA算法,其算法复杂性增加,单次迭代耗时有所增加,但是由于改进算法收敛时的迭代次数减少,其收敛时的总体迭代耗时在4种粒子群算法中最小,为3.24,ms,说明本文的HPSO算法在4种粒子群算法中收敛速度最快.此外HPSO算法收敛时适应度值在各种算法中最小,为1×10-9,说明其求解的开关角度值精度较高.
4 实验验证
为了验证本文所提算法求得开关角度的精确性,本文在两电平三相逆变器硬件系统中完成了实验验证.限于篇幅,本文只对求得的第1组开关角中1/4周期内存在2个开关角和7个开关角的情况进行验证,为了验证求解在整个m范围内的有效性,分别取高调制度(m=0.9)和低调制度(m=0.2)进行实验.所用电路如图6所示.实验中,将前文中HPSO算得的开关角存入FPGA,通过调制算法产生6路PWM波,经驱动电路对逆变器的6个开关管进行控制.由于FPGA的晶振频率为50,MHz,输出电压频率为50,Hz,所以可将一个周期平均分为1×106份,开关角的控制精度可达到3.6×10-4.基波频率为50,Hz时,1/4周期存在2个开关角时的开关频率为250,Hz,存在7个开关角时的开关频率为750,Hz,死区时间都为3,μs.实验采用阻感负载,其中电阻R=12,Ω,电感L=8,mH,直流母线电压为Udc=100,V.

图6 实验电路Fig.6 Experimental circuit
1/4周期内存在2个开关角和7个开关角时的相电压ua、相电压基波分量ua1和三相电流ia、ib、ic的实验波形分别如图7和图8所示.对实验结果进行了傅里叶分析,傅里叶分析的结果如图9所示.
从图7和图8可以看出,相电压波形都保持了半波对称和1/4周期对称,此对称性消除了输出电压的偶数次谐波.由于7个开关角作用下消除的谐波更多,它的电流波形要比2个开关角作用下的好.

图7 N=2时SHEPWM相电压和三相电流波形Fig.7 Phase voltages and three phase current waveforms of SHEPWM with N=2

图8 N=7时SHEPWM相电压和三相电流波形Fig.8 Phase voltages and three phase current waveforms of SHEPWM with N=7

图9 SHEPWM相电压和三相电流波形的傅里叶分析结果Fig.9Fourier analysis diagram of phase voltage and three phase current waveforms of SHEPWM
实验所得的相电压波形ua中,3及3的倍数次谐波依然存在,但线电压和三相电流中这些谐波会因系统的三相对称性抵消为零,所以在进行傅里叶分析时,已经将这些谐波忽略.由式(3)可以算得m分别为0.2和0.9时的参考电压,即相电压基波幅值分别为10,V和45,V,与图7和图8结果一致,证明了算法能够保证基波电压幅值.从图9中(a)~(d)的相电流波形和相电压波形分析结果可以看出,2个开关角的情况下第5次谐波被完全消除,证明了求解结果的精确性;根据式(13)可算得图9中(a)~(d)的相电压HDF分别为1.802,1和0.580,6,与图4中第1组解在m为0.2和0.9时的HDF基本一致.从图9中(e)~(h)的7个开关角作用下的SHEPWM的相电流波形和相电压波形的分析图形中可以看出5、7、11、13、17、19次谐波被完全消除,验证了7个开关角时解的有效性和精确性,同时计算得到m为0.2和0.9时相电压的HDF分别为1.138,4和0.576,8,与图4中计算曲线中的值基本相同,证明了数值算法计算谐波含量的有效性.
5 结 论
(1) 提出的混合粒子群算法改进了权重系数和学习因子的进化方式,采用自适应的调节方法,并将改进的模拟退火算法与粒子群优化算法相结合,能够在保证收敛精度的同时,提高算法收敛速度.
(2) 通过分析SHEPWM开关角方程的特点,将改进的混合粒子群算法用于开关角的求解,消除了传统求解方式对初值的依赖.
(3) 实验验证了本文策略能够准确计算不同情况下SHEPWM的开关角,在求得的开关角作用下,指定次数谐波完全被消除.
[1] Holmes D G,Lipo T A. Pulse Width Modulation for Power Converters:Principles and Practice[M]. USA:John Wiley & Sons,2003.
[2] Patel H S,Hoft R G. Generalized techniques of harmonic elimination and voltage control in thyristor inverters(PartⅠ):Harmonic elimination[J]. IEEE Transactions on Industry Applications,1973(3):310-317.
[3] Patel H S,Hoft R G. Generalized techniques of harmonic elimination and voltage control in thyristor inverters(PartⅡ):Voltage control techniques[J]. IEEE Transactions on Industry Applications,1974(5):666-673.
[4] Kato T. Sequential homotopy-based computation of multiple solutions for selected harmonic elimination in PWM inverters[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,1999,46(5):586-593.
[5] 郑春芳,张波华. 基于 Walsh 变换的逆变器SHEPWM 技术[J]. 电工技术学报,2005,20(5):65-71. Zheng Chunfang,Zhang Bohua. Inverter SHEPWM technique based on Walsh transform[J]. Transactions of China Electrotechnical Society,2005,20(5):65-71(in Chinese).
[6] Agelidis V G,Balouktsis A,Balouktsis I. On applying a minimization technique to the harmonic elimination PWM control:The bipolar waveform[J]. Power Electronics Letters,2004,2(2):41-44.
[7] Agelidis V G,Balouktsis A,Balouktsis I,et al. Multiple sets of solutions for harmonic elimination PWM bipolar waveforms:Analysis and experimental verification[J]. IEEE Transactions on Power Electronics,2006,21(2):415-421.
[8] Dahidah M S A,Agelidis V G,Rao M V. Hybrid genetic algorithm approach for selective harmonic control[J]. Energy Conversion and Management,2008,49(2):131-142.
[9] Darvishi A,Alimardani A,Hosseinian S H. Fuzzy multi-objective technique integrated with differential evolution method to optimise power factor and total harmonic distortion[J]. IET Generation,Transmission and Distribution,2011,5(9):921-929.
[10] Sundareswaran K,Jayant K,Shanavas T N. Inverter harmonic elimination through a colony of continuously exploring ants[J]. IEEE Transactions on Industrial Electronics,2007,54(5):2558-2565.
[11] Kavousi A,Vahidi B,Salehi R,et al. Application of the bee algorithm for selective harmonic elimination strategy in multilevel inverters[J]. IEEE Transactions on Power Electronics,2012,27(4):1689-1696.
[12] 杨 源,余建星,杜尊峰,等. 基于RBFNN 的FDPSO火灾爆炸波及钻井区概率分析[J]. 天津大学学报,2012,45(10):917-923. Yang Yuan,Yu Jianxing,Du Zunfeng,et al. FDPSO fire and explosion spreading to drilling area probability analysis based on RBFNN [J]. Journal of Tianjin University,2012,45(10):917-923(in Chinese).
[13] 赵永满,何 桢,何曙光,等. 基于PSO的支持向量机多元控制图均值偏移诊断模型[J]. 天津大学学报:自然科学与工程技术版,2013,46(5):469-475. Zhao Yongman,He Zhen,He Shuguang,et al. Support vector machine based on particle swarm optimization for monitoring mean shift signals in multivariate control charts[J]. Journal of Tianjin University:Science and Technology,2013,46(5):469-475(in Chinese).
[14] Bao Y,Xiong T,Hu Z. PSO-MISMO modeling strategy for multistep-ahead time series prediction[J]. IEEE Transactions on Cybernetics,2013,44(5):655-668.
[15] 王慧敏,夏长亮,乔照威,等. 双馈风力发电机混合粒子群优化设计[J]. 天津大学学报,2012,45(2):140-146. Wang Huimin,Xia Changliang,Qiao Zhaowei,et al. A hybrid particle swarm optimization algorithm for optimum electromagnetic design of DFIG-based wind power system[J]. Journal of Tianjin University,2012,45(2):140-146(in Chinese).
[16] Gong D W,Zhang Y,Qi C L. Localising odour source using multi-robot and anemotaxis-based particle swarm optimization[J]. IET Control Theory & Application,2012,6(11):1661-1670.
(责任编辑:孙立华)
Selective Harmonic Elimination Pulse Width Modulation Based on Improved Hybrid Particle Swarm Optimization
Chen Wei1,Chen Yujian1,Geng Qiang2
(1.School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China;2.Tianjin Key Laboratory of Advanced Electrical Engineering and Energy Technology,Tianjin Polytechnic University,Tianjin 300387,China)
The requirement of an initial value and the speed of convergence are the main challenges for the traditional iteration method in selective harmonic elimination pulse width modulation(SHEPWM).As to these problems,an improved hybrid particle swarm optimization(HPSO)algorithm was proposed in this paper.In the proposed strategy,the inertia weight and learning factors of PSO algorithm was adjusted.Meanwhile,a new kind of simulated annealing(SA)algorithm,whose temperature coefficient decreases with the increase of the number of iterations,is put forward to combine with PSO,making a favorable improvement in terms of the convergence speed and accuracy compared with the conventional PSO(CPSO)algorithm.Finally,the viability and performance of the proposed strategy are shown through simulation and experimental results in a laboratory prototype.
selective harmonic elimination;optimization algorithm;simulated annealing(SA);hybrid particle swarm optimization(HPSO)
TM464
A
0493-2137(2016)05-0498-08
10.11784/tdxbz201409079
2014-09-30;
2015-01-19.
国家重点基础研究发展计划(973计划)资助项目(2013CB035600);国家自然科学基金资助项目(51577134);天津市应用基础研究计划重点资助项目(13JCZDJC34700).
陈 炜(1977—),男,博士,副教授.
陈 炜,chen_wei@tju.edu.cn.
网络出版时间:2015-09-18. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20150918.1516.002.html.
