低含液率气液两相钝体绕流实验与机理
2016-11-05孙宏军李金霞丁红兵
孙宏军,汪 波,李金霞,丁红兵
(1. 天津大学电气与自动化工程学院,天津 300072;2. 天津市过程检测与控制重点实验室,天津 300072)
低含液率气液两相钝体绕流实验与机理
孙宏军1,2,汪 波1,2,李金霞1,2,丁红兵1,2
(1. 天津大学电气与自动化工程学院,天津 300072;2. 天津市过程检测与控制重点实验室,天津 300072)
气液两相钝体绕流现象广泛存在于生产实践和社会生活中,其中气相中含少量液体是常见的两相流现象.通过实验,研究了常压下50,mm口径水平圆管中低含液率气液两相钝体绕流的涡街现象,就含液率对涡街信号的频率与幅值的影响进行比较分析,应用消除趋势波动法(DFA)对涡街信号进行处理,得到液相体积含率0.1%,左右是本实验条件下能产生稳定涡街的分界点.对实验流型——环状流进行了动力学分析,得到气、液相惯性力之比和液相韦伯数随含液率的变化规律,并从液相的分布与运动及气相夹带液滴对漩涡能量影响两方面,分析了涡街失稳的机理.最后利用拟合的两相斯特劳哈尔数和含液率之间的线性关系,使涡街在湿气及低含液率下的测量误差从6.37%,减小到2.03%,,对实际工程测量有一定的指导意义.
气液两相流;钝体绕流;消除趋势波动法;动力学理论;涡街失稳
钝体绕流现象广泛存在于日常生活和工业生产过程中,其中气液两相钝体绕流是常见的情形,如各种壳管式热交换器、核电站轻水反应堆、湿气输运等.
在一定条件下,流体会在钝体后部形成交替脱落的漩涡,并在尾流中形成周期性卡门涡街.一方面,可以利用漩涡脱落特性进行单相[1]和多相流测量[2];另一方面,交替脱落的漩涡会诱发钝体振动.在流动工况不良的情况下产生的涡街,会引起钝体元件大幅度振动[3]和疲劳损伤,危害工业设备运行的可靠性和安全性.因此,研究气液两相钝体绕流漩涡脱落特性,不仅可以抑制漩涡脱落对工程设备造成的破坏,也可用于研发新型测量仪表,还可以促进气液两相流动力学中两相涡街理论的发展.
国内外学者对气液两相流钝体绕流做了大量有益的探索研究.Hulin等[4]针对垂直上升管双梯形柱体绕流,通过研究气液两相斯特劳哈尔数与液相流量和截面含气率的关系,指出当截面含气率小于10%,时可得到稳定的卡门涡街.Inoue等[5]观测了单圆柱体直径和含气率变化对流场尾迹涡街的影响,测量了柱体附近流场的局部含气率、静压和流速,获取了柱体表面周向压力分布并计算得到柱体所受时均阻力.Shakouchi等[6]研究了气液两相流经单矩形柱体的绕流特性,提出了涡街频率与压降、两相雷诺数的实验关联式.Joe等[7]研究了气液两相绕流单根柱体及绕流管束时其中一根柱体阻力系数和含气率的变化,通过测量含气率分布研究两相绕流特性.李永光等[8]分析了两种尺寸的T形柱体产生涡街时气液两相斯特劳哈尔数的变化规律.卢家才等[9]研究了垂直上升矩形截面管内的气液两相冲刷水平布置的柱体时,斯特劳哈尔数和柱体的脉动升力系数随雷诺数和来流含气率的变化情况.孙志强[10]研究了气液两相流涡街和气液两相绕流的管壁差压特性,定量判别了气液两相流涡街的稳定性,揭示了流型对气液两相绕流压降的影响,发现体积含气率对气液两相流涡街稳定性起主要作用.
气液两相绕流较单相绕流要复杂得多,两相密度相差较大,且两相混合物绕流后回流增强,流场复杂度提高.本文以空气和水为实验介质,研究了常压50,mm口径水平圆管中不同流速和体积含液率下气液两相的钝体绕流特性.
1 涡街原理与实验系统
1.1涡街形成原理
在一定雷诺数(Re)范围内,单相流体流经一非流线形物体(发生体)时,因剪切应力的作用,流体质点脱离原来的轨迹,发生流动分离并产生漩涡.目前常用的发生体为三角柱结构,如图1所示,左侧箭头表示流体运动方向,来流速度为u,压力为p.
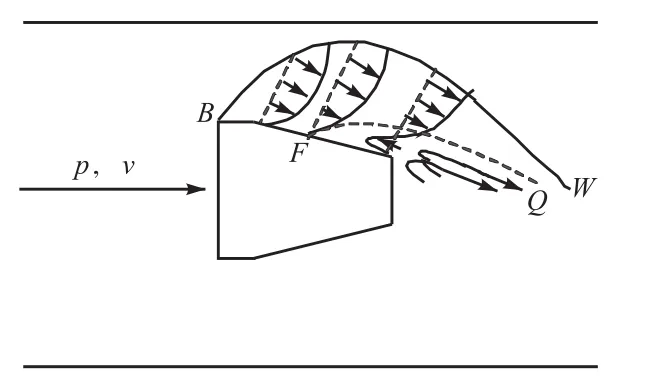
图1 涡街形成机理Fig.1 Mechanism of vortex street
在发生体一侧,流体在F点之后开始出现回流,之后不断地形成一个个漩涡.来流与边界层内倒流的流体相遇,使流线显著地被挤离发生体表面,产生了边界层分离现象.当Re较高时,在发生体两侧就形成了交替的、有规律的漩涡列,形成卡门涡街.
卡门涡街频率f与来流流速v之间的关系可表示为
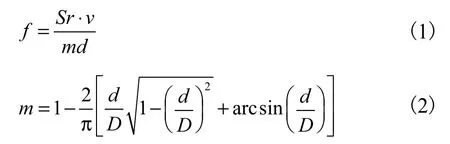
式中:f为漩涡频率,Hz;Sr为斯特劳哈尔数;v为管道来流速度,m/s;d为发生体迎流面的宽度,m;D为管道直径,m.
1.2实验系统
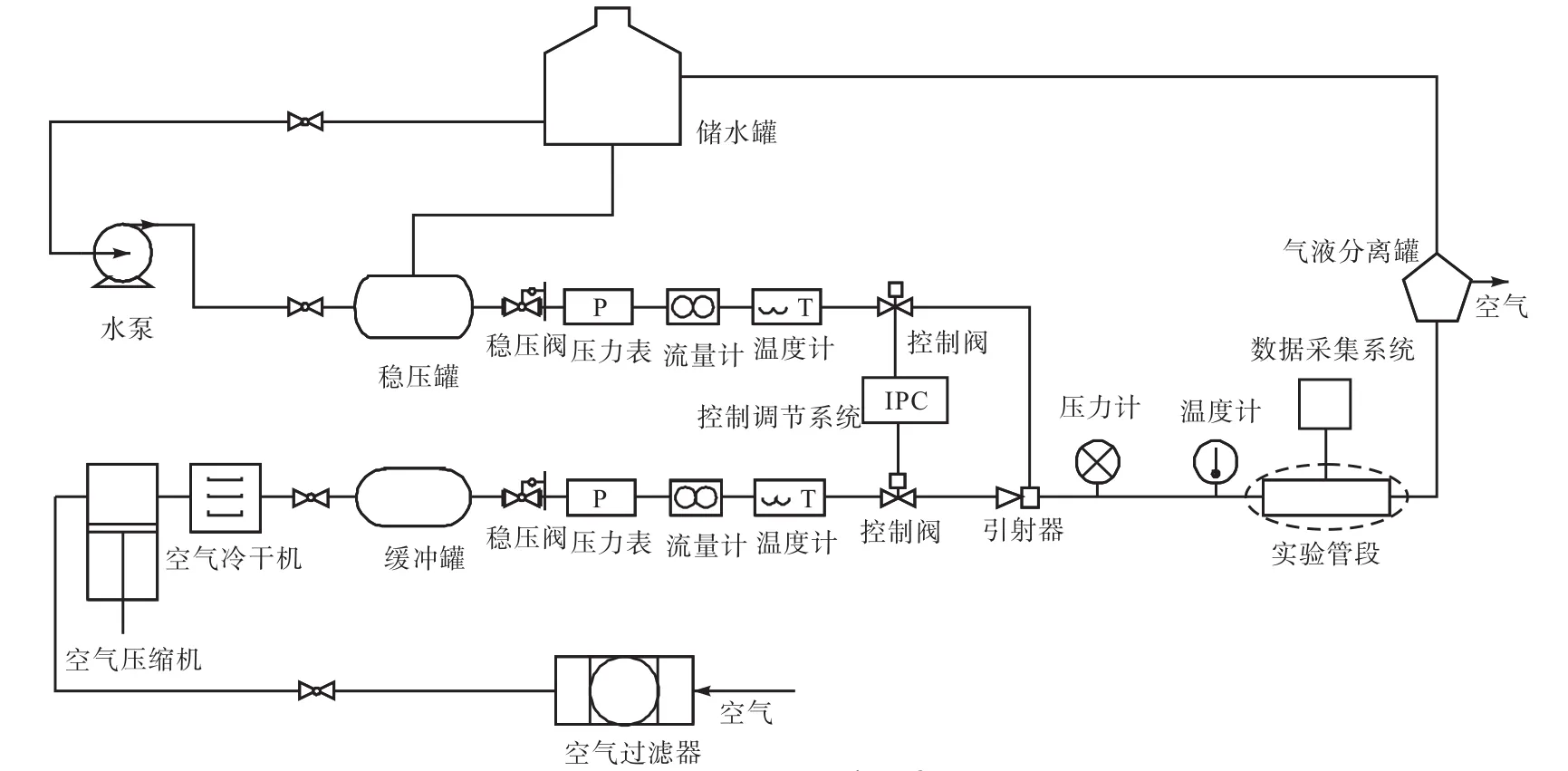
图2 实验系统示意Fig.2 Sketch map of experiment system
实验是在天津大学油气水三相流装置DN50管段上进行的,实验系统如图2所示.空气和水分别经两条独立管路汇通到引射器,从引射器喷出的气液混合流再经过8,m直管段发展后,进入带发生体的实验段.实验条件如下:温度20,℃,表压为14~64,kPa,气相表观速度vsg为22~38,m/s,液体的体积含率β为0~0.6%,,实验管段直径D为50,mm.
涡街发生体尺寸如图3所示,采用三角柱型发生体,既可以产生稳定且强烈的涡街信号,又可在一定程度上减小流体的其他扰动和噪声.为方便观察,前直管段和发生体段均采用透明有机玻璃制作.在发生体后0.5D[11]处打孔,并安装压电探头以检测涡街信号;采用NI6009数据板卡采集数据并连至通过Labview进行实时记录,采样频率为5,000,Hz,每次实验采集5组数据,每组数据采集32,768个点.最后利用Matlab对原始信号进行FFT变换得到频谱(如图4~图9所示),并滤除50,Hz的工频干扰后输出涡街频率.在发生体前5D处进行取压和测温,以检测流场压力和温度变化.
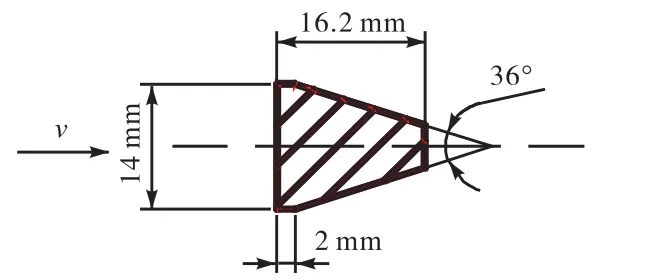
图3 涡街发生体尺寸Fig.3 Size of bluff body
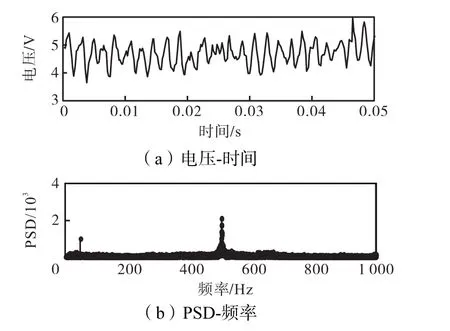
图4 β=0信号序列和频谱(vsg=28.85,m/s)Fig.4 Signals in time domain and spectra with β=0(vsg=28.85,m/s)
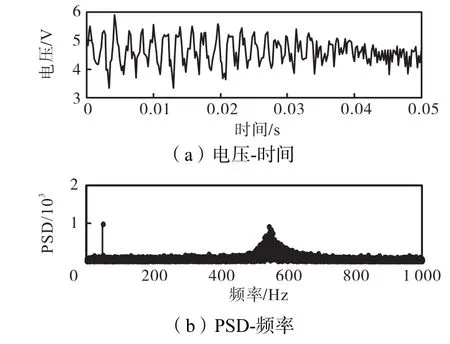
图5 β=0.106%信号序列和频谱(vsg=28.40,m/s)Fig.5 Signals in time domain and spectra with β= 0.106%(vsg=28.40,m/s)
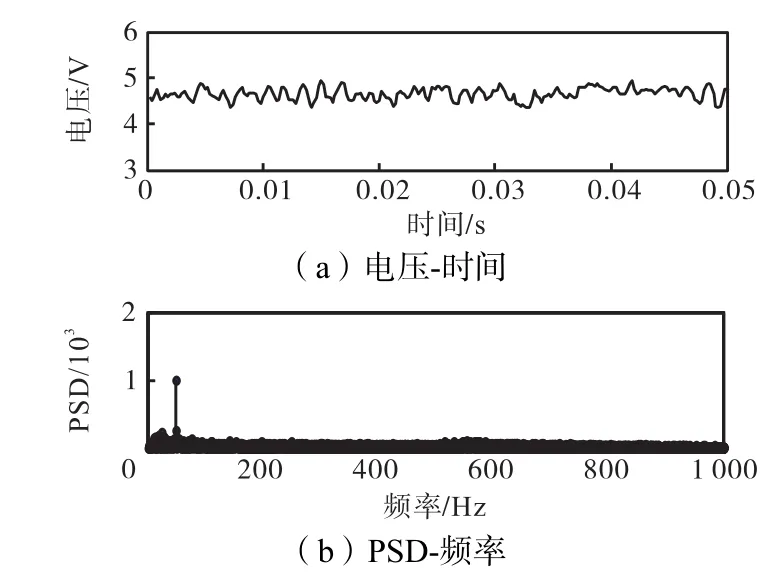
图6 β=0.068%信号序列和频谱(vsg=29.30,m/s)Fig.6Signals in time domain and spectra with β= 0.068%(vsg=29.30,m/s)
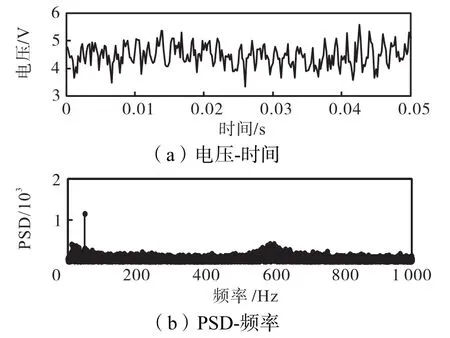
图7 β=0.209%信号序列和频谱(vsg=30.08,m/s)Fig.7Signals in time domain and spectra with β= 0.209%(vsg=30.08,m/s)
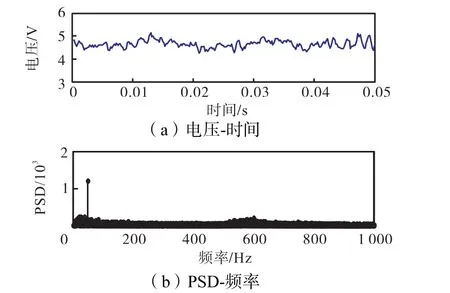
图8 β=0.381%信号序列和频谱(vsg=28.35,m/s)Fig.8Signals in time domain and spectra with β= 0.381%(vsg=28.35,m/s)
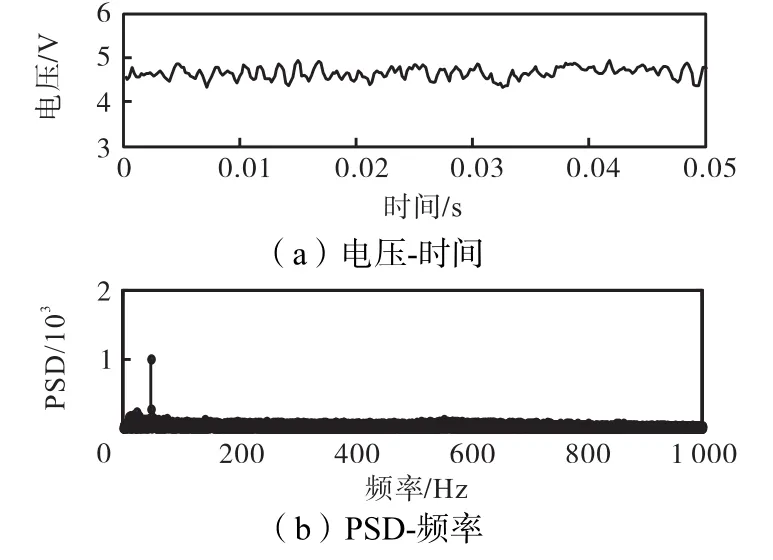
图9 β=0.488%信号序列和频谱(vsg=27.70,m/s)Fig.9Signals in time domain and spectra with β= 0.488%(vsg=27.70,m/s)
2 实验结果与讨论
2.1含液率对涡街信号的影响
对于单相流,在一定Re范围内,流体速度与涡街频率呈线性关系.然而对于气液两相流,液相的加入会对涡街的产生和发展造成影响,且随着液相增多,影响程度会不断增强.
图10为不同含液率下与纯空气介质时的涡街频率与气相表观速度的关系.当含液率较低时,随着含液率增大,两相涡街频率有增大趋势,同时线性度变差.在含液率达到0.34%,~0.38%,时,液相已对稳定涡街产生造成较大影响,此时虽可检测到涡街信号,但其频率与气相表观速度间已不存在明显线性关系,且与纯空气曲线相比有较大的向上平移量.
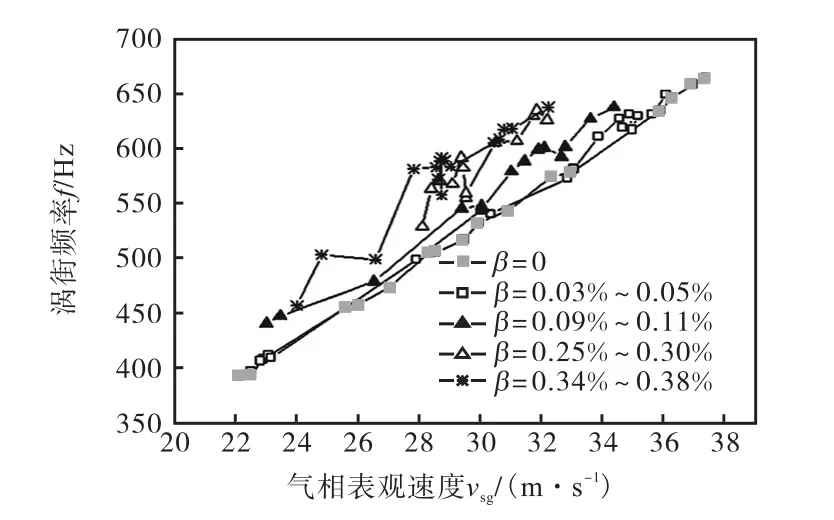
图10 涡街频率-气相表观速度关系Fig.10 Relationship between vortex frequency and gas superficial velocity
另一方面,涡街频率与来流速度可通过式(1)建立函数关系,其中Sr可定量表征涡街的特性.在单相流中,管道Re在2×104~7×106范围内,Sr可以视为常数.然而在多相流中,Sr为变量,其与发生体的形状和Re有关.两相斯特劳哈尔数SrTP计算式为

图11给出了Sr与气相表观速度的关系.在含液率(β=0.03%~0.05%)较小时,气液两相的SrTP与单相Sr相差较小,说明涡街稳定性较好.随着含液率增大,曲线的平稳度变差.当含液率增大到0.34%,~0.38%,时,两相SrTP已经很难再稳定在一个常数附近,利用涡街原理直接进行流体速度的测量也受到限制.两相SrTP较大范围的波动说明涡街流动状态的不稳定,验证了两相流中钝体绕流的随机性与复杂性.通过上述分析可知,含液率对涡街形成有重要影响.为了更深入研究含液率对涡街的作用,保持气相表观速度vsg=30,m/s,得到涡街信号随含液率的变化如图12所示.随着含液率的增大,涡街频率不断增大,而幅值却快速减小.液相的加入使漩涡的复杂性和随机性增强,表现为频率的增大;同时液相的增多也加快了漩涡能量的耗散,表现为升力幅值的减小.此外,大量的实验数据表明含液率0.1%,是一个非常重要的分界点.图13给出了含液率为0.1%,前后信号频率和幅值的重复性散点图.含液率高于0.1%,时,无论是信号的频率还是幅值,重复性都明显增大,但是并没有明确的分界线,因为涡街信号从稳定到不稳定是一个渐变过程.重复性指数的增大,表明过程的随机性增强,说明在β>0.1%,时,压电探头检测到的周期性升力弱于随机性升力,周期性信号被随机性信号所淹没,从而检测不到稳定涡街信号,并导致重复性变差.下面采用消除趋势波动(detrended fluctuation analysis,DFA)法加以验证.
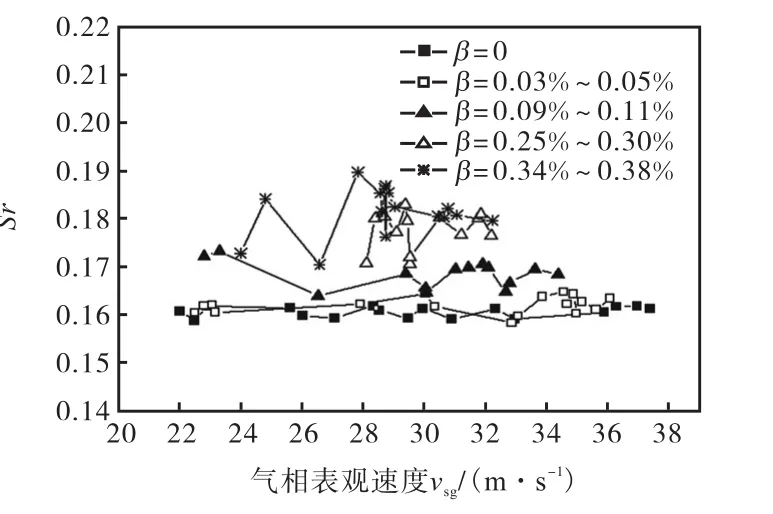
图11 斯特劳哈尔数-气相表观速度关系Fig.11 Relationship between Sr and gas superficial velocity
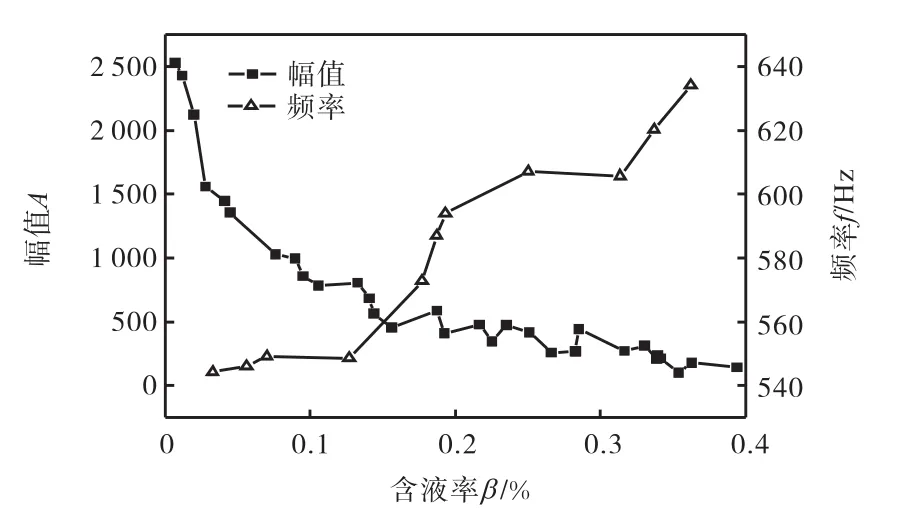
图12 涡街信号随含液率的变化(vsg=30,m/s)Fig.12Relationship between vortex signal and liquid fractions(vsg=30,m/s)
2.2基于消除趋势波动法的信号分析
自20世纪90年代以来,应用分形理论研究多相流越来越普遍,并成为研究多相流的一种重要方法.其中DFA法对4种典型噪声鲁棒性强,表现出良好的抗噪能力[12].本文应用DFA法处理气液两相涡街信号,得出与实验结果相一致的结论.DFA计算过程如下所述[13].
给定一时间序列xi(i=l,2,…,N),其均值为,计算其累加序列y(k)(k=1,…,N)的公式为

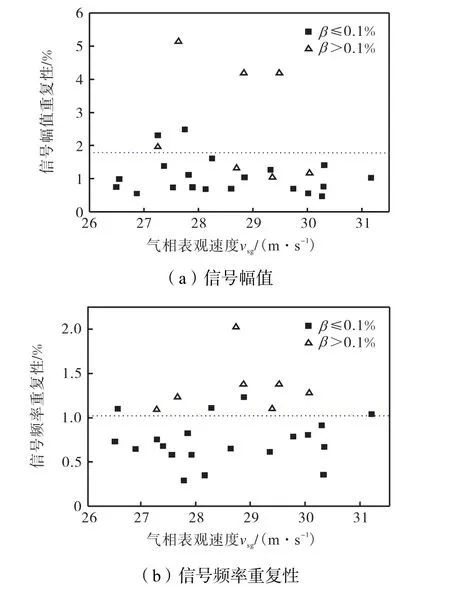
图13 信号重复性-气相表观速度散点图Fig.13 Scatter diagram of signal repeatability and gas superficial velocity
将序列y(k)等分为长度为n的N/n个区间,用最小二乘法分别对每个区间进行一阶线性拟合得到一次函数yn(k),然后计算累加序列y(k)的波动均方根为
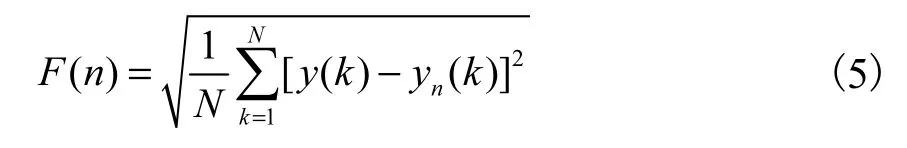
通过变化n值,就可得n与F(n)间的关系为

其在双对数坐标下斜率α 便是分形标度,与平滑系数H的关系:对于分形高斯序列H=α,对于分形布朗运动H=α-1.H可用于描述时间序列长程相关性.
(1) H=0.5,说明时间序列不相关,是一个独立的随机过程,即当前状态不会影响将来状态.
(2) 0.5<H<1.0,说明时间序列具有长程相关性,呈现出趋势不断增强的状态,即在某一时间段是递增(递减)趋势,下一个时间段也会是递增(递减)趋势,且H越大,相关性越强.
(3) 0<H<0.5,说明时间序列只存在负相关性,呈现反持久性的状态,即时间序列在某一时间段是递增(递减)的趋势,则在下一个时间段是递减(递增)的趋势.
为更好地验证算法的可靠性,通过Matlab分别对白噪声和正弦信号(频率为500,Hz)进行了实验验证,结果如表1所示,白噪声的标度指数接近为0.5,而频率值(500,Hz)接近涡街频率的正弦信号的标度指数为0,所以此算法对稳定涡街信号与随机信号有较好的区分度.
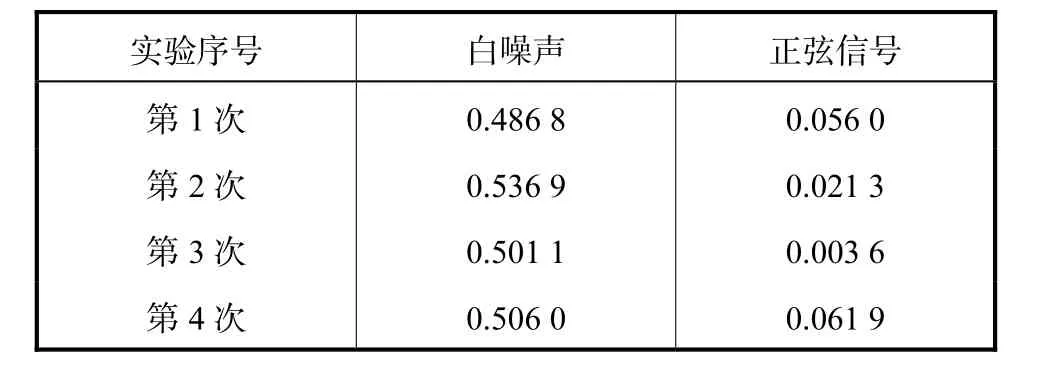
表1 白噪声和正弦信号的标度指数HTab.1Scaling exponent of white nose and sinusoidal signal
图14为标度指数随含液率的变化,图中的标度指数没有超过0.5,说明该过程具有反持久性与负相关性,这与涡街信号性质相符,证明了算法的可靠性.
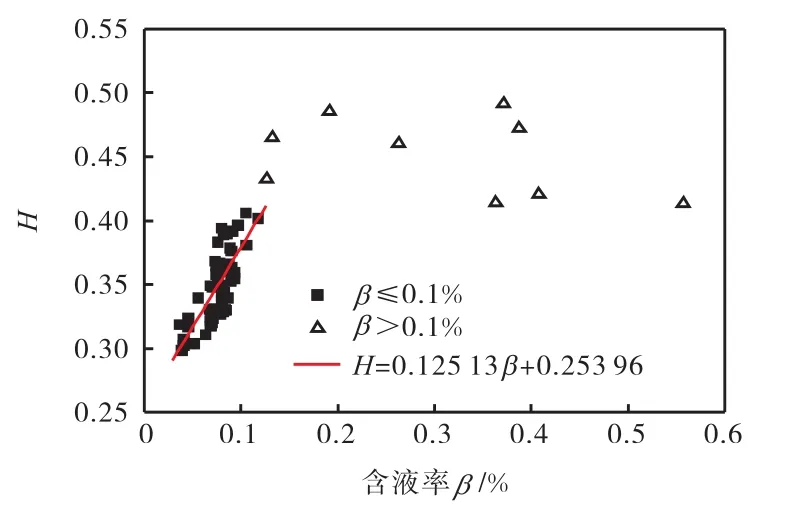
图14 标度指数H随含液率变化Fig.14 Relationship between H and liquid fractions
另外,由图14可知,在β≤0.1%,时,标度指数H随含液率增大而呈规律性变化,具有明显的准线性关系,通过线性拟合得到曲线H=0.125,13,β+ 0.253,96,相关系数R=0.761,78,标准差SD=0.018,2.在β>0.1%,时,标度指数与含液率间无明显规律.
在β≤0.1%,内,随着液相的增多,标度指数呈增大趋势,表明信号时间序列的负相关性减弱,即涡街信号减弱.因此,液相的加入对于涡街信号具有抑制作用.当β>0.1%,时,气液两相的标度指数没有明显规律,说明含液率在0.1%,以上时,漩涡信号受液相影响较强而变得趋向于随机信号.这是因为随着含液率的增大,气相中液滴的聚合碰撞概率增大,而液滴直径的增大会对原本漩涡的生长和发展产生抑制作用.
3 涡街稳定性分析及工程应用
3.1涡街稳定性分析
为了更好地分析涡街失稳的原因,本文首先利用曼德汉(Mandhane)流型图[14]判定实验工况下气液两相流流型,如图15所示.在环状流型中,一般气芯中多少都会夹带一些液滴,将气流的夹带作用考虑在内,流型严格来说应该是环雾状流;管壁上有液膜流动,气流核心为气流和液滴的混合物,界面上的切应力来源于气流与液膜的速度差.
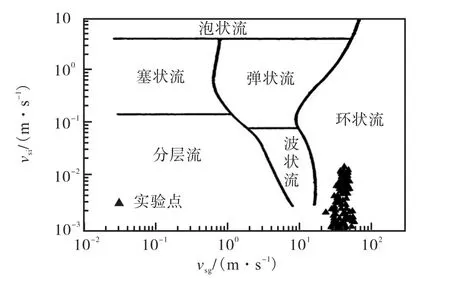
图15 曼德汉流型图Fig.15 Mandhane flow pattern
为了定量比较不同含液率下的力学特征,引入准则数Lockhart-Martinelli参数(L-M参数,X),来表征气液两相惯性力之比,同时以液相韦伯数(Wel)来反映管壁的附着力与表面张力共同作用引起的液相附壁特性,即
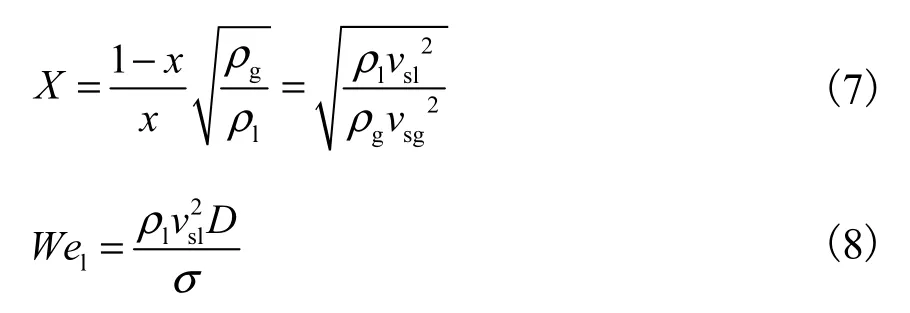
式中:x为质量含气率;ρg为气相密度,kg/m3;ρl为液相密度,kg/m3;vsl为液相表观速度,m/s;D为管道的直径,m;σ.为液相表面张力系数,N/m.
为定量分析X和Wel对气液两相流型的影响,进而研究对漩涡生成和发展的作用,图16比较了不同含液率下X与Wel的大小.当含液率增大时,X值减小而Wel增大,说明气相相对于液相的惯性力减小,液相与壁面的黏附作用增强.这使得液相受气相的加速作用减弱,即液相的增加已使气相无力对所有液相提供加速度,液相就容易积聚成较大的液滴和较厚的液膜,其中漂浮在气芯中的较大液滴,对涡街的形成造成影响,当这种影响足够大时就会破坏稳定漩涡的产生.同时,当含液率在0.1%,左右时,X和Wel随含液率变化的斜率急剧减小和增大,说明此时的流动状态也在剧烈波动,再次证明了含液率0.1%,是一个重要的分界点.
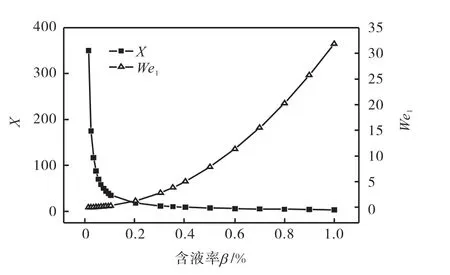
图16 准则数X、Wel与含液率关系Fig.16 Relationship between X and Welwith liquid fractions
3.2低含液率下涡街测量应用
通过上述的实验分析和理论论证,得到含液率在0~0.1%,之间能形成较稳定的漩涡并可以检测到较强涡街信号的结论.为了可以将得到的结论应用于工程实践中,探讨了含液率在0.1%,以下时,β与SrTP之间的关系.
如图17所示,在4种不同流速下,SrTP都是随含液率增大呈上升趋势,变化范围在0.157~0.167之间.如果在低含液率下,涡街的斯特劳哈尔数仍然按单相计算,则会造成6.37%,的误差.通过线性拟合方式得到了含液率0.1%,以下SrTP与β的关系式,即SrTP=0.007,21,β+0.160,02,相关系数R=0.855,16,拟合的标准差SD=0.001,41.含液率在0~0.1%,之间时,利用SrTP与β关系式进行流量的修正,最大误差为2.03%,,明显优于无补偿情况.因此,在工程实际中利用斯特劳哈尔数与β之间的关系可以较大程度地提高涡街在湿气及其他低含液率两相流的测量精度.
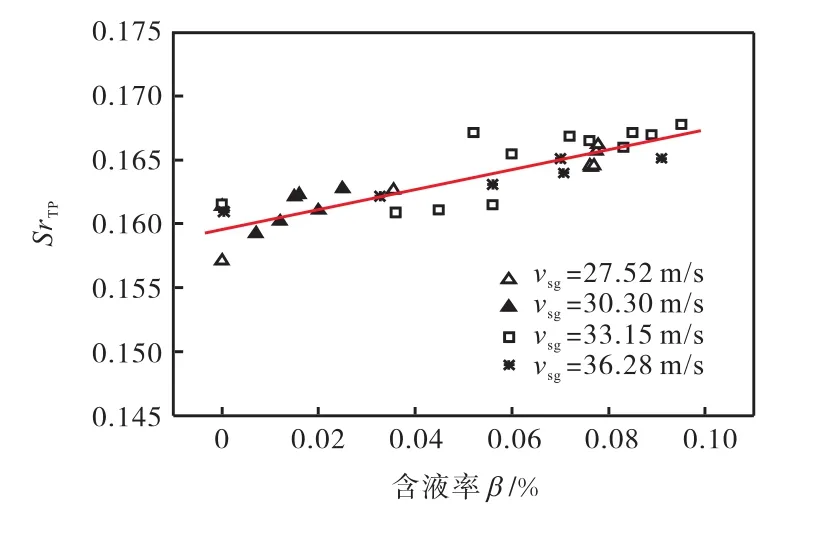
图17 SrTP与含液率关系Fig.17 Relationship between SrTPand liquid fractions
4 结 语
通过实验研究了常压下50,mm口径水平圆管低含液率气液两相钝体绕流中的涡街现象,并与纯空气绕流进行了对比,就含液率对涡街信号频率与幅值的影响进行研究分析,应用DFA法对涡街信号进行处理,得到一个有无稳定涡街信号的重要分界点;通过对环状流的动力学分析,得到不同含液率下,气液相惯性力之比和液相韦伯数的变化规律,最后利用拟合的斯特劳哈尔数与含液率的线性关系提高了涡街在湿气和低含液率下的测量精度;对低含液率水平管气液两相钝体绕流发展进行了有益的探索,为湿气及低含液率的气液两相流测量提供了新的思路.
[1] Zhang Hongjian,Huang Yongmei,Sun Zhiqiang. A study of mass flow rate measurement based on the vortex shedding principle[J]. Flow Measurement and Instrumentation,2006,17(1):29-38.
[2] 贾云飞,张 涛,孔德仁. 涡街流量计在含气液体测量中的试验研究[J]. 南京理工大学学报:自然科学版,2010,34(1):103-107. Jia Yunfei,Zhang Tao,Kong Deren. Experiment of vortex flowmeter used in gas-liquid measurement[J]. Journal of Nanjing University of Science and Technology,2010,34(1):103-107(in Chinese).
[3] Miau J J,Hu C C,Chou J H. Response of a vortex flowmeter to impulsive vibrations[J]. Flow Measurement and Instrumentation,2000,11(1):41-49.
[4] Hulin J P,Fierfort C,Condol R. Experimental study of vortex emission behind bluff obstacles in a gas-liquid vertical two-phase flow[J]. International Journal of Multiphase Flow,1982,8(5):475-490.
[5] Inoue A,Kozawa Y,Youkosawa M,et al. Studies on two phase cross flow(Part I):Flow characteristics around a cylinder[J]. International Journal of Multiphase Flow,1986,12(2):149-167.
[6] Shakouchi T,Tian D,Ida T. Measurement of flow rates of gas-liquid two-phase flow by Karman vortex[C]// Proceedings of the 3rd International Symposium on Measurement Techniques for Multiphase Flows. Japan,2001:83-89.
[7] Joe Y,Dhir V K. An experimental study of drag on a single tube and on a tube in an array under two-phase cross flow[J]. International Journal of Multiphase Flow,1994,20(6):1009-1019.
[8] 李永光,林宗虎. 垂直上升气液两相流中三角形柱体两相斯托拉赫数的研究[J]. 水动力学研究和进展,1999,14(4):438-443. Li Yongguang,Lin Zonghu. Study of gas-liquid twophase Strouhal number for triangle cylinder in vertically upward gas-liquid two-phase flow[J]. Journal of Hydrodynamics,1999,14(4):438-443(in Chinese).
[9] 卢家才,谢正武,林宗虎. 气液两相流中漩涡诱发圆柱振动的脉动升力研究[J]. 应用力学学报,2000,17(1):76-80. Lu Jiacai,Xie Zhengwu,Lin Zonghu. Study on the fluctuating lift acting on a circular cylinder under twophase cross-flow[J]. Chinese Journal of Applied Mechanics,2000,17(1):76-80(in Chinese).
[10] 孙志强. 基于涡街特性的流动分析与参数检测[D]. 杭州:浙江大学电气工程学院,2007. Sun Zhiqiang. Analysis and Measurement of Fluid Flow Using the Characteristics of Vortex Street[D]. Hangzhou:School of Electrical Engineering,Zhejiang University,2007(in Chinese).
[11] 郑丹丹,张 涛. 涡街流量传感器压电探头位置试验研究[J]. 计量学报,2008,29(5):427-433. Zheng Dandan,Zhang Tao. An experimental study of position of piezoelectric probe in vortex flow sensor [J]. Acta Metrologica Sinica,2008,29(5):427-433(in Chinese).
[12] 池 恒. 倾斜及垂直上升管中气液两相流分形标度表征研究[D]. 天津:天津大学电气及其自动化学院,2007. Chi Heng. Study on Fractal Scale Characterization of Inclined and Vertical Upward Gas-Phase Flow Patterns[D]. Tianjin:School of Electrical Engineering and Automation,Tianjin University,2007(in Chinese).
[13] Peng C K,Havlin S,Stanley H E,et al. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series[J]. Chaos,1995,5(1):82-87.
[14] Mandhane J M,Gregory G A,Ariz K. A flow pattern map for gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow,1974,1(4):537-553.
(责任编辑:孙立华)
Experimental and Mechanistic Study on Vortex Flow Around a Bluff Body in Gas-Liquid Flow with Low Liquid Fraction
Sun Hongjun1,2,Wang Bo1,2,Li Jinxia1,2,Ding Hongbing1,2
(1.School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China;2.Tianjin Key Laboratory of Process Measurement and Control,Tianjin 300072,China)
The gas-liquid two-phase flow around a bluff body is widely encountered in the production practicesand social lives.In this study,the vortex flow around a bluff body in 50,mm-caliber horizontal gas-liquid two-phase flow with low liquid fractions at normal pressure was investigated by experiments.The effects of liquid fractions on the frequency and amplitude of vortex signal were discussed,and then,vortex signals were processed by detrended fluctuation analysis(DFA).A characteristic liquid volume fraction around 0.1%, for the stability of vortex street was attained.The relationship of liquid fractions with gas-liquid phase inertia forces and the liquid Weber number were discussed respectively by the dynamics analysis for annular flow.The law of vortex street instability was analyzed.It was found that the energy of vortex street would be dissipated by liquid phase and entrained droplets.The error of gasliquid two phase flow with low liquid fractions and moisture measure decreased from 6.37%, to 2.03%, by setting up the linear relationship of two-phase Strouhal number and liquid fractions,which is instructional in actual engineering.
gas-liquid two-phase flow;flow around bluff body;detrended fluctuation analysis (DFA);kinetic theory;vortex street instability
O0359.2
A
0493-2137(2016)05-0491-07
10.11784/tdxbz201504099
2015-04-30;
2015-09-28.
国家自然科学基金青年基金资助项目(50906061).
孙宏军(1974—),女,博士,副教授,sunhongjun@tju.edu.cn.
汪 波,oneboy232@163.com.
网络出版时间:2016-01-14. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20160114.1431.002.html.
